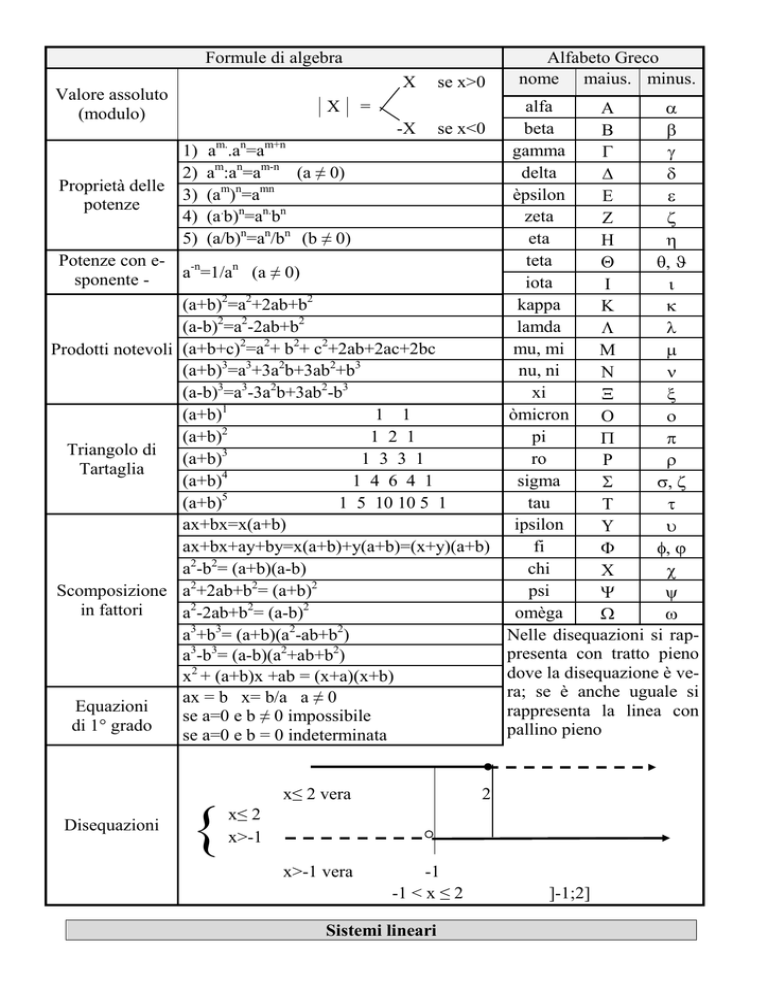
Formule di algebra
X
Valore assoluto
(modulo)
se x>0
Alfabeto Greco
nome maius. minus.
alfa
-X se x<0
beta
m. n
m+n
1) a .a =a
gamma
m n
m-n
2) a :a =a
(a ≠ 0)
delta
Proprietà delle
m n
mn
3) (a ) =a
èpsilon
potenze
. n
n. n
4) (a b) =a b
zeta
n
n n
5) (a/b) =a /b (b ≠ 0)
eta
Potenze con e- -n
teta
n
a
=1/a
(a
≠
0)
sponente iota
2
2
2
(a+b) =a +2ab+b
kappa
2
2
2
(a-b) =a -2ab+b
lamda
2
2
2
2
mu, mi
Prodotti notevoli (a+b+c) =a + b + c +2ab+2ac+2bc
3
3
2
2
3
(a+b) =a +3a b+3ab +b
nu, ni
3
3
2
2 3
(a-b) =a -3a b+3ab -b
xi
1
(a+b)
1 1
òmicron
2
(a+b)
1 2 1
pi
Triangolo di
3
(a+b)
1 3 3 1
ro
Tartaglia
4
(a+b)
1 4 6 4 1
sigma
5
(a+b)
1 5 10 10 5 1
tau
ax+bx=x(a+b)
ipsilon
ax+bx+ay+by=x(a+b)+y(a+b)=(x+y)(a+b)
fi
2 2
a -b = (a+b)(a-b)
chi
2
2
2
psi
Scomposizione a +2ab+b = (a+b)
2
2
2
in fattori
a -2ab+b = (a-b)
omèga
3
3
2
2
a +b = (a+b)(a -ab+b )
Nelle disequazioni si rap3 3
2
2
presenta con tratto pieno
a -b = (a-b)(a +ab+b )
2
dove la disequazione è vex + (a+b)x +ab = (x+a)(x+b)
ra; se è anche uguale si
ax = b x= b/a a ≠ 0
Equazioni
rappresenta la linea con
se a=0 e b ≠ 0 impossibile
di 1° grado
pallino pieno
se a=0 e b = 0 indeterminata
X
=
x≤ 2 vera
Disequazioni
{
2
x≤ 2
x>-1
x>-1 vera
-1
-1 < x ≤ 2
Sistemi lineari
]-1;2]
{
ax + by = c
a1x + b1y = c1
Sostituzione
Confronto
a/a1 ≠ b/b1
a/a1 = b/b1= c/c1
a/a1 = b/b1≠ c/c1
y = 5 – 4x
Determinato se
è Indeterminato se
Impossibile se
4x + y = 5
{
{
{
{
{
3x - 2y = 12
y = 5 – 4x
3x -2(5-4y) = 12
x=2
y = 5 – 4.2 = -3
y = 5 – 4x
{
x=2
4x + y = 5
3x – 2y = 12
y = 5 – 4x
y = -3
x=2
y = 5 – 4x
5 – 4x = (3x-12)/2
y = (3x-12)/2
x=2
{
y = 5-4.2 = -3
y = -3
{
x=2
x=2
x=2
Nella riduzione, se i coefficienti di x o y sono diversi, si moltiplica in modo che o x
o y diventino uguali e si sommano algebricamente in modo da annullare o x o y
Eliminiamo x
Eliminiamo y
4x + y = 5
8x + 2y = 10
12x + 3y = 15
3x – 2y = 12
3x – 2y = 12
12x – 8y = 48
Riduzione
11x
= 22
11y = -33
x=2
y = -3
4x + y = 5
4x + y = 5
{
{
{
{
Cramer
{
{
y = -3
a
4x + y = 5
3x – 2y = 12
4
3 -2
Dx
x=
a1
b1
4
-22
-11
= 33
3 12
Dy
=2
5
= -22 Dy=
Dx=
12 -2
=
D
= ab1 – ba1
5 1
= -11
D=
b
D=
1
x=2
y=
33
=
D
= -3
-11