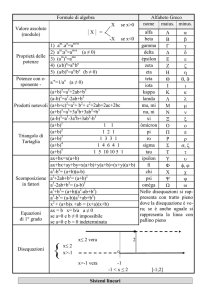
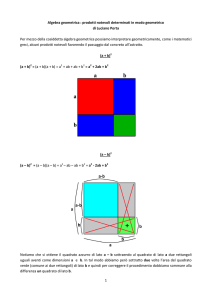
PERCORSO DI RECUPERO SUL CALCOLO LETTERALE – 1
In matematica l’uso di lettere al posto dei numeri nasce dall’esigenza di non limitarsi a considerare casi
particolari ma di generalizzare proprietà valide sempre, quindi indipendenti dallo specifico valore
numerico.
Un po' come quando, in geometria, si esprime con una formula il procedimento per calcolare un’area.
Ad esempio, l’area di un triangolo si calcola moltiplicando la misura della base per la misura dell’altezza e
dividendo il risultato per due. Se indichiamo con A l’area, con b la base e con h l’altezza, possiamo scrivere
A = (b x h) : 2
Il simbolo della moltiplicazione (x) può essere sostituito da un puntino (∙) per non confonderlo con la lettera
x, spesso usata anche per indicare un valore incognito, e il simbolo della divisione (:) può essere sostituito
dalla linea di frazione. La formula diventa, quindi
che è equivalente alla precedente.
Questa formula esprime una proprietà generale, valida per tutti i triangoli, indipendentemente dalla misura
della base e dalla misura dell’altezza.
Quando la applichi per calcolare l’area di uno specifico triangolo sostituisci alle lettere b e h il loro valore
numerico ed effettui le operazioni indicate dalla formula
Esempio, calcola l’area di un triangolo la cui base misura cm 21 e l’altezza cm 16.
DATI: b = 21 cm;
h = 16 cm
A = 21 cm∙ 16 cm /2 = 168 cm2
L’unità di misura delle aree è sempre elevata al quadrato; nel nostro esempio cm ∙ cm = cm2
Anche quando hai studiato le proprietà delle potenze hai avuto a che fare con delle formule, valide per
qualsiasi valore della base.
Ad esempio am ∙ an = am+n
Se a = 2, m= 3, n = 4 la formula diventa 23 ∙ 24 = 23+4 = 27
Tutto qui. Nel calcolo letterale il simbolo della moltiplicazione, già ridotto ad un puntino, si può omettere. In
altri termini, se non è presente nessun simbolo di operazione è sottintesa la moltiplicazione.
Ad esempio, invece di a ∙ b si scrive ab; invece di 2 ∙a ∙ b si scrive 2ab.
Le lettere rappresentano dei numeri relativi (positivi o negativi, interi o fratti ..).
Ovviamente, posso addizionare e sottrarre le stesse entità, anche se non conosco il loro valore numerico.
Esempi
2ab + 3ab = 5ab
7ab – 3ab = 4ab
-3ab + 5ab = +2ab
4ab – 6ab = -2ab
Non posso, invece, addizionare o sottrarre entità diverse tra loro come, ad esempio ab e cd, finché non
conosco il loro valore numerico perché, come abbiamo detto, le lettere rappresentano dei numeri relativi
qualsiasi, però due lettere uguali rappresentano sicuramente due numeri relativi uguali e due lettere
diverse rappresentano sicuramente due numeri relativi diversi.
Nel calcolo letterale le entità si chiamano monomi
Un monomio è costituito da numeri e lettere, legati tra di loro dalle operazioni di moltiplicazione e/o
divisione, tipo
2ab
x3 y
Se non c’è il numero è sottinteso 1
I monomi che hanno la stessa parte letterale si chiamano monomi simili; posso addizionarli o sottrarli tra
loro
Quindi, se mi trovo di fronte ad un’espressione del genere
3ab + 5a – 7a
Posso fare la somma algebrica di + 5a e – 7a e semplificare l’espressione:
3ab + 5a – 7a = 3ab - 2a
Due monomi simili che hanno la stessa parte numerica e diverso segno si chiamano opposti. La loro somma
è sempre zero!
Esempio
+ 7xy3 - 7xy3 = 0
PROVA TU
Semplifica le seguenti espressioni:
3ab + 2c – 8ab – 3c + 6c
2x – 3xy + 4x – 2xy
Se dobbiamo calcolare il valore di un’espressione letterale per specifici valori numerici corrispondenti alle
lettere, conviene procedere come nel seguente esempio. Quando sarai più sicuro, potrai fare i calcoli a mente
Calcola che valore assume l’espressione 2ab + 3a2– 2b
per a = -2
2(-2)(+3) + 3(-2)2 - 2(+3) =
+2(-6) + 3(+4) - 6 =
-12 + 12 – 6 = - 6
PROVA TU
Calcola il valore della seguente espressione letterale, per a = -3
-5a + 2ab – 3b
Controlla i risultati di seguito
b = +2
b=+3
3ab + 2c – 8ab – 3c + 6c = -5ab + 5c
2x – 3xy + 4x – 2xy = +6x – 5xy
(per a = -3
b = +2)
-5a + 2ab – 3b = -5(-3) +2(-3)(+2) -3(+2) = +15 -12 – 6 = - 3