Algebra geometrica : prodotti notevoli determinati in modo geometrico
di Luciano Porta
Per mezzo della cosiddetta algebra geometrica possiamo interpretare geometricamente, come i matematici
greci, alcuni prodotti notevoli favorendo il passaggio dal concreto all’astratto.
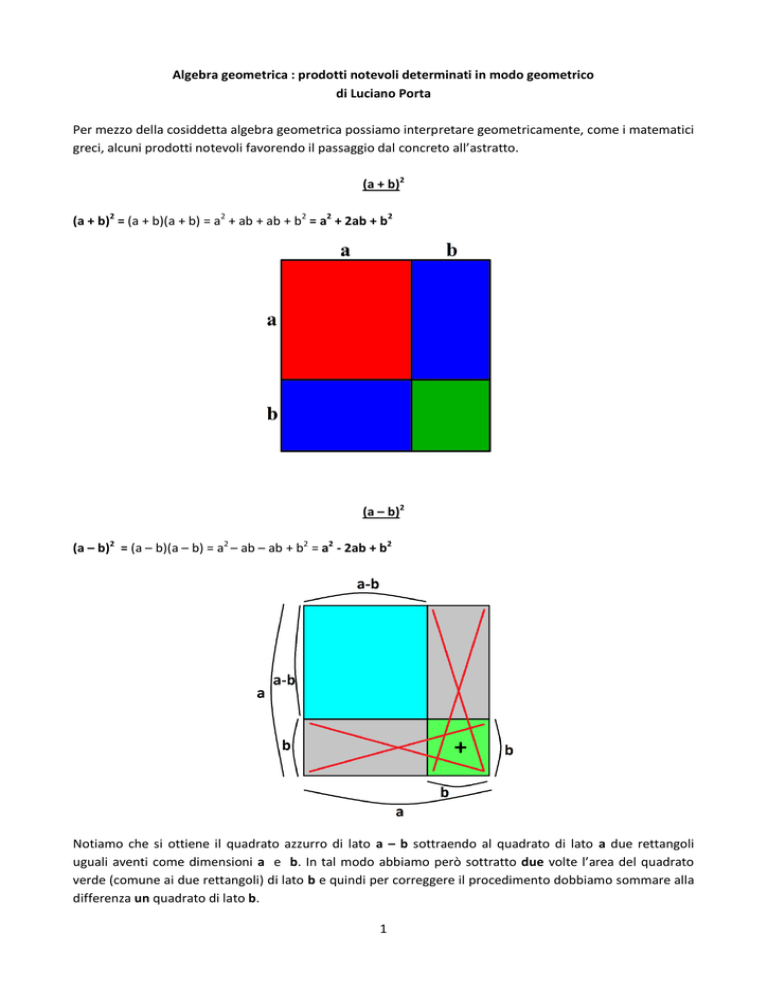
(a + b)2
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
(a – b)2
(a – b)2 = (a – b)(a – b) = a2 – ab – ab + b2 = a2 - 2ab + b2
Notiamo che si ottiene il quadrato azzurro di lato a – b sottraendo al quadrato di lato a due rettangoli
uguali aventi come dimensioni a e b. In tal modo abbiamo però sottratto due volte l’area del quadrato
verde (comune ai due rettangoli) di lato b e quindi per correggere il procedimento dobbiamo sommare alla
differenza un quadrato di lato b.
1
(a + b + c)2
(a + b + c)2 = (a + b + c)(a + b + c) = a2 + ab + ac + ab + b2 + bc + ac + bc + c2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
(a + b)3
(a + b)3 = (a + b)(a + b)(a + b) =(a2 + 2ab + b2)(a + b) = a3 + a2b + 2a2b + 2ab2 + ab2 + b3 = a3 + 3a2b + 3 ab2 + b3
Osserviamo che ogni faccia del cubo rappresenta il prodotto notevole (a + b)2 = a2 + 2ab + b2 .
(a + b)(a – b)
(a + b)(a - b) = a2 –ab + ab – b2 = a2 – b2
www.webalice.it/lucianoporta i Pitagorici DIDATTICA E DIVULGAZIONE DELLA MATEMATICA E DELLE SCIENZE LEZIONI DUE
2