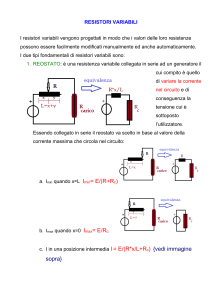
SCHEDA CORRENTI ALTERNATE
(V. Colagrande)
ε = ε max sin (ωt )
Generatore di corrente alternata con f.e.m.:
CA
Circuiti Semplici
Circuito
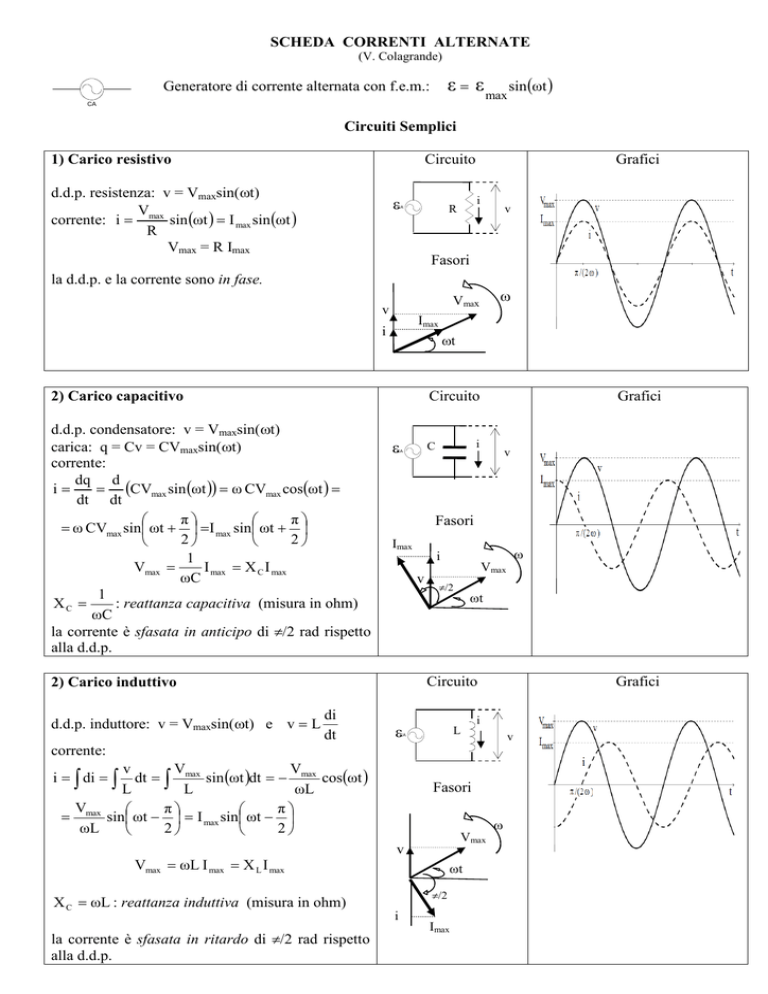
1) Carico resistivo
d.d.p. resistenza: v = Vmaxsin(ωt)
V
corrente: i = max sin (ωt ) = I max sin (ωt )
R
Vmax = R Imax
ε
i
R
CA
Grafici
v
Fasori
la d.d.p. e la corrente sono in fase.
Imax
i
ωt
Circuito
2) Carico capacitivo
d.d.p. condensatore: v = Vmaxsin(ωt)
carica: q = Cv = CVmaxsin(ωt)
corrente:
dq d
i=
= (CVmax sin (ωt )) = ω CVmax cos(ωt ) =
dt dt
π
π
= ω CVmax sin ωt + = I max sin ωt +
2
2
1
Vmax =
I max = X C I max
ωC
1
XC =
: reattanza capacitiva (misura in ohm)
ωC
la corrente è sfasata in anticipo di π/2 rad rispetto
alla d.d.p.
ε
Grafici
i
C
CA
v
Fasori
Imax
ω
i
v
Vmax
π/2
ωt
Circuito
2) Carico induttivo
d.d.p. induttore: v = Vmaxsin(ωt) e v = L
ω
Vmax
v
di
dt
Grafici
i
ε
L
CA
v
corrente:
V
V
v
dt = ∫ max sin (ωt )dt = − max cos(ωt )
L
L
ωL
V
π
π
= max sin ωt − = I max sin ωt −
ωL
2
2
i = ∫ di = ∫
Vmax = ωL I max = X L I max
X C = ωL : reattanza induttiva (misura in ohm)
la corrente è sfasata in ritardo di π/2 rad rispetto
alla d.d.p.
Fasori
ω
Vmax
v
ωt
π/2
i
Imax
Circuiti RLC serie
Circuito
ε = ε max sin (ωt )
i= I
sin (ωt + ϕ )
max
f.e.m.
corrente
R
ε
ϕ = costante di fase: angolo di sfasamento
L
CA
tra tensione e corrente.
C
Indicate con vR, vC e vL le d.d.p. ai capi di R, C e L rispettivamente, per la seconda legge di Kirchhoff, in
qualunque istante di tempo si ha:
ε= v +v +v .
R
C
L
Per determinare la corrente i, si fa riferimento alla rappresentazione con i fasori.
Fasori
Dall’analisi dei circuiti semplici:
vR e i sono in fase
i
vC è in ritardo di π/2 rad rispetto a i
vR
vL è in anticipo di π/2 rad rispetto a i
ε
Vmax,L
Vmax,R = R Imax
vL
Vmax,C = XC Imax
Imax
A
OA =Vmax,R
Vmax,R
ϕ
ωt
B
εmax
AB =Vmax,C − Vmax,L
OB =εmax
O
Vmax,L = XL Imax
vC
Vmax,C
Nella rappresentazione con i fasori si è
ipotizzato un circuito più capacitivo che
induttivo (XC > XL). Inoltre il triangolo di
vertici OAB è retto in A.
Vmax,C − Vmax,L
Applicando il teorema di Pitagora al triangolo OAB si ha:
ε 2max
2
(
) (
)
2
2
= R I
+ V
−V
+ X I
−X I
⇒ I
=
c max
L max
max, R max, C
max, L
max
max
= V2
ε max
(
R + X −X
2
c
2
se L = 0 e C = ∞ ⇒ Z = R;
1
1
1
Z = R + (X c − X L ) = R +
− ωL = impedenza
se
− ωL = 0 ⇒ ω =
: risonanza.
ωC
ωC
LC
Dal grafico dei fasori si può ricavare l’ampiezza di fase ϕ:
2
2
2
AB = OA ⋅ tg ϕ ⇒ tg ϕ =
AB Vmax, C − Vmax, L X C I max − X L I max X C − X L 1 ωC − ωL
=
=
=
=
.
Vmax, R
RI max
R
R
OA
XC > XL ⇒ tg ϕ > 0 ⇒ la corrente i è sfasata in anticipo di ϕ rispetto alla f.e.m. ε;
XC < XL ⇒ tg ϕ < 0 ⇒ la corrente i è sfasata in ritardo di ϕ rispetto alla f.e.m. ε;
L = 0 e C = ∞ ⇒ tg ϕ = 0 ⇒ la corrente i e la f.e.m. ε sono in fase.
)
2
L
.