CdL in CH-CHI-STM-SA Esame scritto di Istituzioni di Matematica

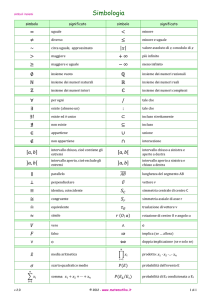
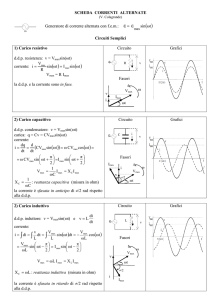
CdL in CH-CHI-STM-SA
Esame scritto di Istituzioni di Matematica – Appello estivo del 18.06.2010
B
Parte I.
Studiare una delle seguenti funzioni:
1.A


1
 ( x  1)( x  2) 

f ( x)  ln  2
  ln 
x

5
x

6
(
x

3
)(
x

5
)




(Vmax= 8/30)
1.B
 ( x  3) (5  x) 1 
f ( x)  ln 
e 
2
 x  5 x  6



 
_______________________________
(Vmax= 10/30)
Risolvere una delle seguente equazioni differenziali [funzione incognita: y(x)]:
2.A
2 y dy  ( y 2  1) dx
(Vmax= 5/30)
con la condizione al contorno: y (0)  0
[si suggerisce la soluzione per sostituzione di (y2-1) ; considerare solo la soluzione positiva].
2.B
(3x  3) 2
f ( x)
 e
x
1




 ( x 1) 


 e1
con la condizione al contorno: f (2)  0
(Vmax= 3/30)
(si suggerisce la risoluzione per scomposizione e poi per sostituzione dell’esponente)
_______________________________
3. Si sviluppi in serie di McLaurin arrestata al second’ordine la funzione:
 1 
f ( x)  sen 
e si calcoli l’errore percentuale massimo ( % max ) di
 x  1
approssimazione per x=0.2:
 % max  ?
(archi in radianti)
(Vmax=4/30)
Parte II
1. VERO/FALSO (E’ obbligatorio giustificare sinteticamente le risposte)
a) Se una funzione y=f(x) è lineare, allora y è direttamente proporzionale a x.
b) La funzione y=
ln x  non è approssimabile con la formula di Taylor con punto iniziale x0= -2.
c) In una equazione differenziale del secondo ordine la funzione incognita compare sempre con
esponente 2.
d) La retta y=x ha pendenza dell’ 1%.
e) Se la relazione tra due variabili x e y è di proporzionalità inversa , ciò implica che y dipende
linearmente da 1/x.
f) Condizione necessaria affinché una funzione f(x) non nulla abbia media integrale nulla nell’intervallo
[a,b] è che f(x) non abbia lo stesso segno in tutti i punti di [a,b]
g) L’integrale definito di una funzione polinomiale intera in un intervallo chiuso è sempre finito.
h) La funzione integrale di una funzione f(x) continua in un dato intervallo [a;b] è continua su tutto
l’intervallo.
i) Data una funzione f(x) con dominio x ≤0, se f(0)<0 allora la pendenza iniziale di f(x) è negativa.
l) l) L’integrale definito nell’intervallo [-a;a] di una funzione antisimmetrica e non costante su tutto
l’intervallo non è mai nullo.
(Vmax= 10)
2. Argomentare la correttezza o la falsità della seguente affermazione:
“Data una funzione f(x) derivabile nell’intervallo [a;b], la sua funzione integrale può o non può
essere derivabile, a seconda della forma di f(x)”.
2.Derivare la funzione f(x)=
ln( x  1)
ln  x 
4. Risolvere la disequazione:


 (2  x) 
0
ln 
 2  
 1  x  


(Vmax= 2)
(Vmax= 2)