LABORATORIO DI OTTICA GEOMETRICA
Esperienza n. 1: Misura del raggio di curvatura di una superficie sferica
Strumenti a disposizione:
sferometro
Descrizione dell’esperienza:
a) Determinare lo “zero” ho dello strumento ponendo lo sferometro sul piano di riferimento (lastra di
vetro ben levigata), con una serie di N=20 misure in punti diversi del piano; disegnare l’istogramma
delle misure e determinare il valor medio di ho con il suo errore (deviazione standard della media):
σh =
∑ (h
0i
− h0 ) 2
N −1
0
σh =
0
σh
0
N
b) Misurare l’altezza H della calotta sferica in un punto centrale di essa, individuata dai tre piedi dello
sferometro, con N=50 misure ripetute nello stesso punto. Disegnare l’istogramma delle misure e
determinare il valor medio di H ed il suo errore:
σH =
∑ (H
i
− H )2
N −1
σH =
σH
N
c) Determinare:
σh =
h = H − h0
σ H2 + σ h
2
0
ed il raggio di curvatura della superficie come:
1
R =
2
(
ρ2
h
+ h
)
σ
R
1
ρ2
=
1− 2 σh
2
h
dove ρ è definito in figura; si noti che si considera trascurabile l’errore su ρ.
e) Ripetere la procedura in altri punti della calotta. Dalle misure effettuate dei raggi di curvatura in vari
punti si può dedurre che la calotta è sferica ?
Lo sferometro
Vista dall’alto
Vista di lato
P1
P1
d
h
ρ
P2
d
ρ
P2
30°
ρ ⋅ cos 30 ° =
P3
d
d
2
ρ =
d
2
⋅
=
2
3
sferometro “Galilei”:
ρ = 50 mm
sferometro “Leybold”:
d = 50 mm
R
d
3
2° teorema di Euclide:
da cui:
2R − h : ρ = ρ : h
1
R=
2
ρ2
(h
+h
)
LABORATORIO DI OTTICA GEOMETRICA
Esperienza n. 2: Misura dell’indice di rifrazione di un prisma di vetro
Strumenti a disposizione:
a) Laser
b) goniometro con tubo di mira
c) prisma di vetro
In questa esperienza ci si propone di misurare l'indice di rifrazione di un vetro relativamente alla
radiazione emessa da un laser a stato solido con λ= 670 nm . A questo scopo si utilizza un prisma di
vetro.
NON guardare il fascio laser ad occhio nudo, né direttamente né attraverso il tubo di mira, per evitare
danni alla retina.
Posizionare il prisma di vetro con lo spigolo approssimativamente al centro del supporto come indicato
in figura.
Ruotare il prisma ed osservare che l’angolo δ di deviazione varia, al variare dell’angolo di incidenza i
ma è comunque maggiore o uguale di un angolo δmin . Misurare e riportare su un grafico almeno 10
coppie di valori (i,δ
δ) in modo da evidenziarne l’andamento.
Eseguire misure ripetute (almeno 30) di δmin in modo da determinarne il valor medio e l’errore
statistico.
laser
i
α
supporto con
goniometro
δ
tubo di mira
Sapendo che il valore di α è 60° (α=1.0472 rad) con errore trascurabile, determinare l’indice di
rifrazione n del vetro per la luce del laser a disposizione:
n=
sin (
α + δ min
sin (
2
α
2
)
)
1
σn =
2
cos (
α + δ min
2
α
sin ( )
2
)
⋅ σ δ min
LABORATORIO DI OTTICA GEOMETRICA
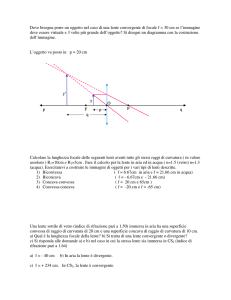
Esperienza n. 3: Misura della distanza focale di una lente sottile
Strumenti a disposizione:
righello, banco ottico con cavalieri, proiettore ad alogeni, oggetto da proiezione su supporto, schermo
traslucido, lente 40/100
schermo
lente
Y1
Y2
p
q
Dopo aver misurato le dimensioni trasversali Y1 dell’oggetto, lo si ponga sul banco ottico; si posizioni
il proiettore obliquamente rispetto al banco ottico in modo che la luce non incida direttamente sulla
lente e non si surriscaldi l’oggetto.
Variando la posizione dell’oggetto (almeno 6-7) sul banco ottico, misurandone la coordinata p rispetto
alla lente, considerata come lente sottile, si misurino le dimensioni Y2 e l’ascissa q dell’immagine
raccolta sullo schermo, come in figura.
Per tener conto della “profondità di messa a fuoco” si ripeta la misura almeno 5 volte per ogni
posizione dell’oggetto e se ne ricavi la media. Per l’errore, di tipo “massimo”, si consideri la
semiampiezza dell’intervallo delle misure ottenute, ovvero: ∆q = (qmax - qmin)/2. Analogamente per
l’errore massimo su Y2, cioè: ∆Y2 = (Y2max - Y2min)/2.
Si tracci il grafico di q in funzione di p e si grafichi anche l’ingrandimento trasversale GY = Y2 /Y1 in
funzione di p.
Graficare, inoltre, 1/q in funzione di 1/p.
Sfruttando la legge dei punti coniugati, valida in approssimazione di raggi parassiali:
1 1
1
+ =
p q
f
si ricavi dalla regressione lineare non pesata
1
1 1
= −
q
f
p
che è del tipo y = A + B x con:
y=
1
q
x=
1
p
A =
1
f
B = −1
la distanza focale della lente:
f =
1
A
σ
f
=
1
2 σ
A
Il valore di f così misurato è compatibile con quello nominale ?
A
LABORATORIO DI OTTICA GEOMETRICA
Esperienza n. 4:
Misura dell'ingrandimento visuale di una lente di ingrandimento
Strumenti a disposizione:
a) righello
b) banco ottico con cavalieri
c) sorgente luminosa
d) oggetto di proiezione
e) schermo traslucido
f) lente da 40/100 e 75/150
Questa esperienza consiste nella misura degli ingrandimenti visuali di una lente convergente, utilizzata
come lente di ingrandimento e di un microscopio composto. A questo scopo si utilizza un modello
d'occhio costituito da una lente 75/150 (“cristallino”) e dallo schermo (“retina”) per visualizzare le
immagini virtuali prodotte dagli strumenti e misurare gli angoli visuali.
1) Scegliere un oggetto che abbia un verso (affinché si possa determinare l'orientazione sua e
dell'immagine rispetto all'asse ottico) e dimensioni trasversali (≤ 2 cm) tali che si possa ritenere
valida l'approssimazione di Gauss.
2) Misurare le dimensioni trasversali Y1 dell'oggetto e montarlo su un cavaliere in corrispondenza
dell'origine della scala graduata sul banco ottico, preoccupandosi che il piano dell'oggetto sia
perpendicolare al banco ottico.
3) Disporre il cavaliere con il cristallino alla distanza di visione distinta d0 = 25 cm. dall'oggetto.
Il piano della lente deve essere perpendicolare al banco ottico, i centri dell'oggetto e della lente
devono essere allineati e paralleli al banco ottico.
4) Montare la “retina” del modello d’occhio dalla parte opposta del “cristallino” rispetto all'oggetto.
5) Disporre la sorgente luminosa (per illuminare l'oggetto ed avere un'immagine brillante) obliqua
rispetto al banco ottico affinché la luce non incida direttamente sulla lente e abbastanza distante
dall'oggetto per evitare il surriscaldamento con conseguente deformazione.
6) Determinare l'ascissa qr come punto medio dell'intervallo (qmin , qmax ) di “messa a fuoco”
dell’immagine, determinare le dimensioni Yr in modo analogo e calcolare l'angolo visuale αr
dell'immagine retinica come rapporto tang αr = Yr / qr.
L’errore di misura ∆qr da attribuire alla coordinata qr sarà di tipo “massimo” e pari alla
semilarghezza dell’intervallo (qmin , qmax ), cioè: ∆qr = (qmax - qmin)/2. Analogamente per l’errore
massimo su Yr, cioè: ∆Yr = (Yrmax - Yrmin)/2. L’errore su tang αr è dato semplicemente dalla
propagazione degli errori massimi: ∆ tang αr / tang αr = ∆Yr / Yr + ∆qr / qr (si ricordi che nel caso
di un rapporto o di un prodotto si sommano gli errori massimi relativi).
7) Montare sul banco ottico la lente 40/100 a una distanza dall'oggetto p < f = 100 mm. In tal modo la
lente diventerà un oculare positivo, produrrà un'immagine virtuale e sarà utilizzata come lente
d'ingrandimento.
8) Porre il “cristallino” nel secondo fuoco della lente di ingrandimento.
9) Fissata la posizione dell’oggetto, ovvero la coordinata p2 rispetto alla lente, raccogliere l'immagine
sulla “retina”, misurarne l'ascissa q2, le dimensioni Y2 e l'angolo visuale βr. Per gli errori valgono
le stesse considerazioni di cui al punto 6).
10) Determinare l'ingrandimento visuale Gα che, per piccoli angoli, può scriversi come
Gα = tang βr /tang αr . Anche qui l’errore percentuale su Gα è valutabile come somma degli errori
percentuali.
11) Ripetere le operazioni del punto 9) al variare dell'ascissa p dell'oggetto allo scopo di ottenere
almeno 5 stime diverse dell'ingrandimento visuale.
12) Tabulare i dati e riportare su grafico Gα in funzione di p.
13) Stabilire se le diverse stime di Gα sono compatibili tra di loro e indipendenti da p.
14) Ricavare la migliore stima dell'ingrandimento visuale Gα e confrontarlo con il valore Gα = d0 / f
previsto dalla teoria in tale configurazione (ovvero con l’“occhio” nel secondo fuoco della lente).
cristallino
fC = 150 mm
Schermo
(retina)
Y
αr
Yr
fC
d0
qr
f = 100 mm
schermo
(retina)
cristallino
fC = 150 mm
y1
y
βr
y2
p
q
p2
d=f
fC
q2
LABORATORIO DI OTTICA GEOMETRICA
Esperienza n. 5:
Misura dell'ingrandimento visuale di un microscopio composto
Strumenti a disposizione:
a) righello
b) banco ottico con cavalieri
c) sorgente luminosa
d) oggetto di proiezione
e) schermo traslucido
f) lenti da 40/50, 40/100 e 75/150
Questa esperienza consiste nella misura dell’ingrandimento visuale di un microscopio composto. A
questo scopo si utilizza un modello d'occhio costituito da una lente 75/100 (cristallino) e dallo schermo
(retina) per visualizzare le immagini virtuali prodotte dagli strumenti e misurare gli angoli visuali.
1) Scegliere un oggetto che abbia un verso (affinché si possa determinare l'orientazione sua e
dell'immagine rispetto all'asse ottico) e dimensioni trasversali sufficientemente piccole (≤ 2 cm) a
causa delle limitazioni imposte dalla pupilla d'uscita del microscopio e tali che si possa anche
ritenere valida l’approssimazione di Gauss.
2) Montare l’oggetto e montarlo su un cavaliere in corrispondenza dell'origine della scala graduata sul
banco ottico, preoccupandosi che il piano dell'oggetto sia perpendicolare al banco ottico.
3) Disporre il cavaliere con il cristallino alla distanza di visione distinta do = 25 cm. dall'oggetto.
Il piano della lente deve essere perpendicolare al banco ottico, i centri dell'oggetto e della lente
devono essere allineati e paralleli al banco ottico.
4) Montare la “retina” dalla parte opposta del “cristallino” rispetto all'oggetto.
5) Disporre la sorgente luminosa (per illuminare l'oggetto ed avere un'immagine brillante) obliqua
rispetto al banco ottico affinché la luce non incida direttamente sulla lente e abbastanza distante
dall'oggetto per evitare il surriscaldamento con conseguente deformazione.
6) Misurare l'ascissa qo e la dimensione Yo dell'immagine retinica e determinare l’angolo visuale
tang αr = Yo / qo. L’errore di tipo massimo su tang αr si ottiene come propagazione degli errori
massimi su Yo e su qo.
cristallino
f=150 mm
Schermo
(retina)
Y
αo
Yo
do
fc
qo
7) Lasciando l'oggetto all'inizio del banco ottico, montare a una distanza p > 5 cm dall'oggetto una
lente obiettivo con fob = 5 cm, ed a 35 cm da quest'ultimo la lente che funge da oculare con foc = 10
cm. Si realizza così un microscopio composto con tiraggio meccanico T=35 cm e lunghezza ottica
∆=20 cm.
8) Disporre il cristallino nel secondo fuoco Foc dell'oculare, cioè ad una distanza pari a foc.
9) Lasciando fisso il microscopio, mettere a fuoco l'immagine retinica, variando, molto lentamente,
(dato che la profondità di campo del microscopio è limitata) e sempre per valori p > fob, la distanza
dell'oggetto dall'obiettivo fino ad ottenere un'immagine nitida.
10) Misurare le dimensioni Yr, l'ascissa qr e determinare l'angolo visuale tang βr = Yr / qr. L’errore di
tipo massimo su tang βr si ottiene come propagazione degli errori massimi su Yr e su qr.
11) Ricavare l'ingrandimento visuale del microscopio Gv = tang βr / tang αr e l’errore corrispondente
∆ Gv come propagazione degli errori massimi su tang βr e su tang αr.
∆ d0
12) Confrontare il valore misurato con la previsione teorica: G v =
.
f ob f oc
schermo
cristallino
fc= 150 mm
T
obiettivo
oculare
foc= 100 mm
fob= 50 mm
y1
F1
βr
∆
ob
F2
ob
Yr
yob
F1
oc
F2
yoc
oc
qr
foc
Nota importante:
L’ingrandimento visuale del microscopio composto ed il suo errore massimo possono anche essere
determinati senza passare attraverso il calcolo esplicito degli angoli visuali, utilizzando direttamente le
misure effettuate:
Gv ≡
tang β r
Y q
= r o
tang α r q r Yo
∆Y
∆q r ∆Yo ∆q o
∆G v = r +
+
+
qr
Yo
qo
Yr
G v