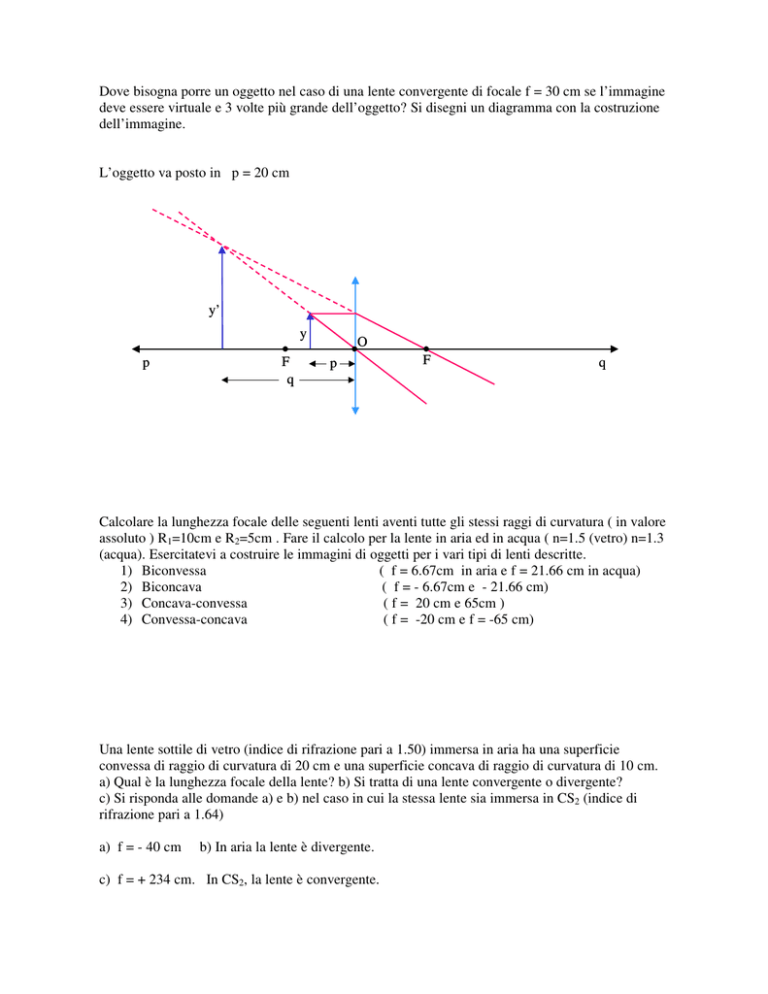
Dove bisogna porre un oggetto nel caso di una lente convergente di focale f = 30 cm se l’immagine
deve essere virtuale e 3 volte più grande dell’oggetto? Si disegni un diagramma con la costruzione
dell’immagine.
L’oggetto va posto in p = 20 cm
y’
p
.
F
q
y
.
O
p
.
F
q
Calcolare la lunghezza focale delle seguenti lenti aventi tutte gli stessi raggi di curvatura ( in valore
assoluto ) R1=10cm e R2=5cm . Fare il calcolo per la lente in aria ed in acqua ( n=1.5 (vetro) n=1.3
(acqua). Esercitatevi a costruire le immagini di oggetti per i vari tipi di lenti descritte.
1) Biconvessa
( f = 6.67cm in aria e f = 21.66 cm in acqua)
2) Biconcava
( f = - 6.67cm e - 21.66 cm)
3) Concava-convessa
( f = 20 cm e 65cm )
4) Convessa-concava
( f = -20 cm e f = -65 cm)
Una lente sottile di vetro (indice di rifrazione pari a 1.50) immersa in aria ha una superficie
convessa di raggio di curvatura di 20 cm e una superficie concava di raggio di curvatura di 10 cm.
a) Qual è la lunghezza focale della lente? b) Si tratta di una lente convergente o divergente?
c) Si risponda alle domande a) e b) nel caso in cui la stessa lente sia immersa in CS2 (indice di
rifrazione pari a 1.64)
a) f = - 40 cm
b) In aria la lente è divergente.
c) f = + 234 cm. In CS2, la lente è convergente.
Un oggetto è posto ad una distanza di 65 cm da una lente convergente di lunghezza focale f = 40
cm. A quale distanza dalla lente si forma l’immagine? E’ un’immagine reale o virtuale? Quanto
vale l’ingrandimento? Disegnare un diagramma con la costruzione dell’immagine.
q = 104 cm
L’immagine è reale.
L’ingrandimento è G = 1.6
p
p
.
f1
O
.
f2
q
q
Un microscopio ha una lunghezza ottica D = 20 cm, un obbiettivo con focale f1=10 mm e un
oculare con focale f2= 20 mm. L’apertura numerica, n sen α , sia N.A. = 0.7. La distanza del punto
prossimo dell’occhio è d0=25cm.
a) Costruite lo schema del microscopio mostrando il disegno per costruire l’immagine
b) Calcolare l’ingrandimento del microscopio
( G = 250 )
c) Calcolare la profondità di campo
( ∆p = 3.7 × 10-4 cm = 3.7 µm )
d) Calcolare il potere risolutivo (luce di λ = 0.5 µm)
( 1/dmin = 1 / 0.36 µm )
-4
e) Assumendo come acuità visiva dell’occhio θ = 3 × 10 rad, verificare se l’ingrandimento del
microscopio è sufficiente per sfruttare al pieno il potere risolutivo. Se non lo è, calcolare quale
dovrebbe essere l’ingrandimento. (Basta in teoria un ingrandimento di 210)












