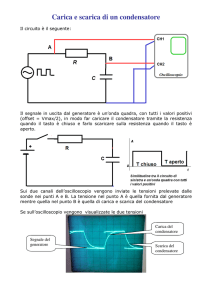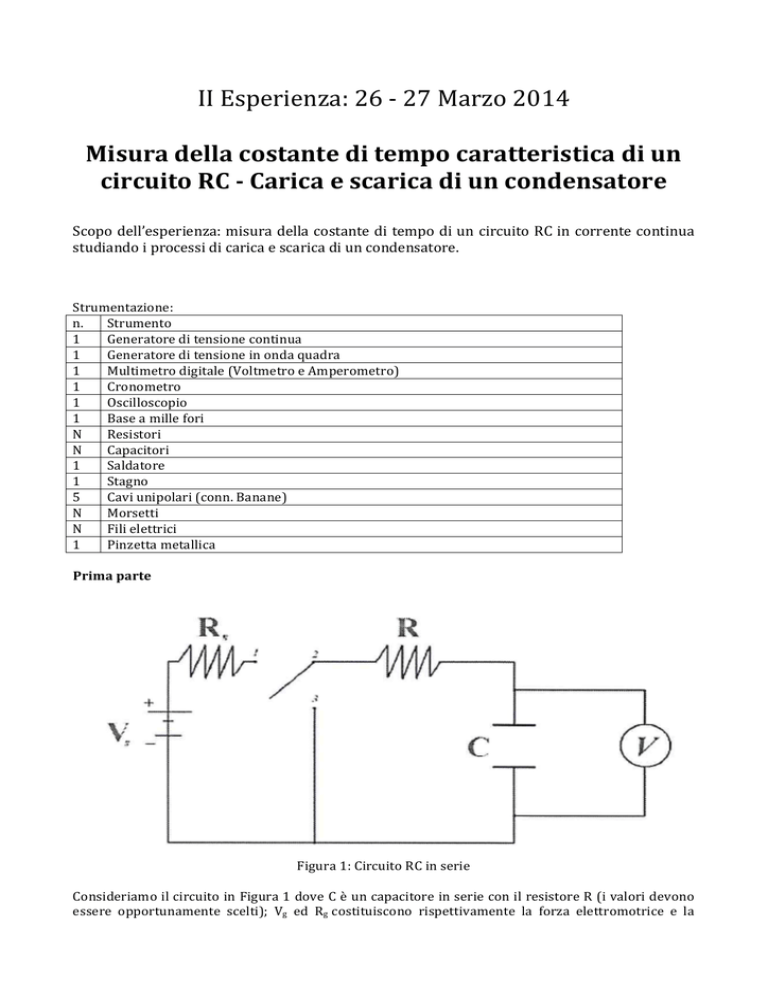
II Esperienza: 26 -­‐ 27 Marzo 2014 Misura della costante di tempo caratteristica di un circuito RC -­ Carica e scarica di un condensatore Scopo dell’esperienza: misura della costante di tempo di un circuito RC in corrente continua studiando i processi di carica e scarica di un condensatore. Strumentazione: n. Strumento 1 Generatore di tensione continua 1 Generatore di tensione in onda quadra 1 Multimetro digitale (Voltmetro e Amperometro) 1 Cronometro 1 Oscilloscopio 1 Base a mille fori N Resistori N Capacitori 1 Saldatore 1 Stagno 5 Cavi unipolari (conn. Banane) N Morsetti N Fili elettrici 1 Pinzetta metallica Prima parte Figura 1: Circuito RC in serie Consideriamo il circuito in Figura 1 dove C è un capacitore in serie con il resistore R (i valori devono essere opportunamente scelti); Vg ed Rg costituiscono rispettivamente la forza elettromotrice e la resistenza interna di un generatore di tensione costante. Il circuito è dotato di un interruttore che consente di inserire (1-­‐2) o di cortocircuitare (2-­‐3) un generatore che fornisce una tensione continua. Quando si chiude l’interruttore nella posizione (1-­‐2), nella maglia scorre una corrente I(t) data da: Vg = I(t) ( Rg + R) + 1/C ∫I(t)dt (1) Ponendo: Vc (t)=1/C ∫I(t)dt (2) derivando si può scrivere: C dVc(t)/dt = I(t) (3) da cui: Vg = C ( Rg + R) dVc(t)/dt + Vc (t) (4) La soluzione generale di questa equazione è data da: Vc (t)= C1 exp(-­‐t/τ) + Vg (5) Dove: τ = τc = (R+Rg) C posizionando il contatto su (1-­‐2): 0 𝑡 ≤ 0
𝑉! = {
𝑉! 𝑡 > 0
posizionando successivamente il contatto su (2-­‐3): 𝑉 𝑡 ≤ 0
𝑉! = { ! 0 𝑡 > 0
C1 si determina dalle condizioni iniziali. a) Carica del condensatore Vc( 0) = 0 e Vg=V0 Vc (0)= C1 + V0 = 0 da cui C1= -­‐ V0 Vc (t)= V0[1-­‐exp(-­‐t/τ)] (6) Scegliendo opportunamente i valori di R e C si monta il circuito di Figura 1. Si misurano i valori della tensione ai capi della capacità misurati a partire dal momento in cui l’interruttore viene posto nella posizione (1-­‐2) (ovvero quando si collega il generatore al circuito), ad intervalli di tempo costanti. Dalla (6) si ha che: [V0-­‐Vc (t)]/ V0= exp(-­‐t/τ) da cui: ln {[V0-­‐Vc (t)]/ V0} = -­‐t/τ che, rappresentata in carta semi-­‐logaritmica in funzione del tempo t, permette di determinare il valore di τ dalle rette di massima e minima pendenza. b) Scarica del condensatore Vc( 0) = V0 e Vg=0 τ =RC . Vc (0)= C1 = V0 da cui C1= V0 Vc (t)= V0exp(-­‐t/τ) (7) Spostando successivamente l’interruttore sulla posizione (2-­‐3) (ovvero s collega il generatore a condensatore carico), si misurano i valori della tensione ai capi della capacità ad intervalli di tempo costanti. Dalla (7) si ha che: Vc (t)/ V0= exp(-­‐t/τ) da cui: ln [Vc (t)/ V0] = -­‐t/τ che, permette di determinare nuovamente il valore di τ. Seconda parte R + Rg Figura 2: Circuito RC in serie alimentato in onda quadra. Consideriamo lo schema circuitale rappresentato in Figura 2, dove Vg è la tensione erogata da un generatore di tensione ad onda quadra, di ampiezza V0 e periodo T. !!
!
𝑛𝑇 ≤ 𝑡 < 𝑛𝑇 +
!
!
Vc(t) ={ !!
!
− 𝑛𝑇 + ≤ 𝑡 < (𝑛 + 1)𝑇
!
!
Si misura la tensione ai capi della capacità C, utilizzando un oscilloscopio. Il fronte di salita dell’onda quadra può essere assimilata all’accensione del generatore di tensione continua, cui segue la carica del condensatore (eq. 6). Il fronte di discesa, può essere assimilato allo spegnimento del generatore, cui fa seguito la scarica del condensatore (eq. 7). La soluzione è data dalla relazione periodica: Vc(t) =
{
!
𝑉!
!
−
!
𝑉!
!
(!!!")
!
!
!
!!! !!
!
!
!
(!!!"! )
!
!
!!!
!
!!!
𝑛𝑇 ≤ 𝑡 < 𝑛𝑇 +
!
!
−
!
𝑛𝑇 +
!
!
(8) ≤ 𝑡 < (𝑛 + 1)𝑇
!
a) τ >>T/2 L’andamento esponenziale si può approssimare con uno lineare: !!
−𝑉!
Vc(t)={ 𝑉!
!
!
!
!!!!!!
!
!!
!
!!!!
!
!!
−
−
!
!
!
= 𝑉!
!
!
!
!
!!!!
!
!! !
!
!
!
!!
!!
!! = −𝑉!
!! !!!
!
! !!!!
!!
!
!! !!!
!
!!
!
! !!
!!
− = 𝑉!
!!
Vc(t) ={
( !!
−
!
!
!! !
( !
!!
!
!
!
!!
=
!!
!
=
!! !!
!
!!
(
!
!!
−
(
) 𝑛𝑇 ≤ 𝑡 < 𝑛𝑇 +
!!
!!
−
!!
!
!
− = −𝑉!
!
) 𝑛𝑇 +
!
!
!
!
−
!
!!
) 𝑛𝑇 ≤ 𝑡 < 𝑛𝑇 +
) 𝑛𝑇 +
!
!
!
!
≤ 𝑡 < (𝑛 + 1)𝑇
!
!
≤ 𝑡 < (𝑛 + 1)𝑇
(9) La capacità non ha il tempo né di caricarsi, né di scaricarsi completamente. Il modulo della tensione massima è: Vmax = V0 (T/8τ) << V0 b) τ <<T/2 La capacità ha tutto il tempo di caricarsi e di raggiungere la tensione del generatore: 𝑉!
!
!
−
Vc(t)={
𝑉!
!
!
(!!!")
!
!
!
!!! !!
!
!
!
(!!!"! )
!
!
!!!
!
!!!
−
!
≅ 𝑉!
!
!
!
−𝑒
≅ 𝑉! 𝑒
!
!!!"
!
!
(!!!"! )
!
!
!
c) τ ~T/2 Valgono le relazioni generali. Vc_max/min={
𝑉!
𝑉!
!
𝑛𝑇 ≤ 𝑡 < 𝑛𝑇 +
−
! !!
!
!!! !!
!!
!
!
!!! !!
−
!
!
!
−
!
!
𝑛𝑇 +
!
!
(10) (11) ≤ 𝑡 < (𝑛 + 1)𝑇
≈ 0.23 𝑉! 𝑡 =
!
!
≈ − 0.23 𝑉! 𝑡 = 𝑇
Verificare sperimentalmente tali relazioni utilizzando letture dei valori di tensione misurati ai capi della capacità in funzione del tempo, tramite l’oscilloscopio. Riportare sul grafico in carta opportunamente scelta gli andamenti (9) e (10)misurati nei casi a) e b). Verificare la relazione (11) nel caso c).