I Pitagorici - Liceo Mazzini

I Pitagorici
Con i Pitagorici ci troviamo per la prima volta di fronte ad
un'autentica scuola filosofica, sebbene molto arcaica e
rudimentale. Siamo nel VI secolo a.C. e la scuola filosofica
assume il carattere di scuola mistica, basti pensare che per
entrare a far parte della scuola bisognava essere sottoposti ad un
rito di iniziazione, in un certo senso si può anche parlare di
"setta" religiosa, i cui membri conducevano vita comune. Tutti i
pensatori che lavorarono in questa scuola vengono
generalmente chiamati Pitagorici, dal nome del loro maestro
Pitagora.
di Masciullo Ginevra 2^ G
COME SI VIVEVA NELLA SCUOLA
PITAGORICA?
• Nella scuola l'insegnamento, originariamente, non era
affidato allo scritto, ma era impartito oralmente.
• Le dottrine della scuola andavano mantenute segrete e
i frequentatori erano tenuti al silenzio
• Era diffusa la pratica di non mangiare carni, fave e
fagioli
• Si credeva nella trasmigrazione delle anime
• Bisognava vivere in modo giusto,sano e compiere riti
• Conoscere i numeri, che stanno alla base della dottrina
pitagorica
La realtà passa per i numeri
Tutte le cose si possono misurare, la
fisica è spiegabile tramite la
matematica, I numeri come gli astri
sono fissati nello spazio.
Ci sono delle somiglianze tra le
caratteristiche dei numeri e quelle
della realtà.
Il numero 2 corrispondeva al
genere femminile
Il 3 al maschile
• Il cinque al matrimonio ( 3 +2 = 5).
Il 4 ed il 9 corrispondevano invece alla giustizia
in quanto erano i primi numeri quadrati e
suggeriscono l'idea di ordine.
Il numero 10 è considerato un numero perfetto
in quanto somma dei primi quattro numeri
(1+2+ 3+ 4) che, disposti su quattro linee in
ordine crescente, secondo una
rappresentazione grafica puntiforme, formano
la tetraktys, cioè il triangolo equilatero
formato da 10 punti con il lato di 4.
La tetraktys era considerata figura sacra.
Si devono ai pitagorici anche le seguenti
scoperte:
-Le tavole pitagoriche
-la formula per il calcolo della somma degli
angoli interni di un poligono
-la costruzione dei solidi regolari
- la dipendenza degli intervalli musicali da
precise relazioni di lunghezza delle corde
A Pitagora viene attribuita anche
l'ideazione della TAVOLA PITAGORICA
che costituisce il più importante
approccio al calcolo numerico.
• Alcuni contributi dei Pitagorici alla geometria
sarebbero le dimostrazioni che la somma degli
angoli interni di un triangolo vale 180°
• Studio di almeno 3 solidi regolari :
Tetraedro
cubo
dodecaedro
• Il primo tentativo di scala musicale lo si deve a
Pitagora.Utilizzando un monocordo e le proprietà
delle frazioni costruì la prima scala musicale
"teorizzata”, essa è puramente "formale" e
"quadrata" dal punto di vista numerico dei rapporti
tra le varie note. In genere, quando si suddivide un
intervallo continuo lo si fa con punti equidistanti.
Come la matematica influenza la
musica
• Se prendiamo una corda che produce un determinato
suono e desideriamo ottenere il suono superiore di
un'ottava, dobbiamo interrompere la corda nel suo punto
centrale. Indicando con A la lunghezza della corda che
produce il primo suono e con B la lunghezza della sezione
che produce il secondo, abbiamo che A: B = 2 :1.
Per salire di una quinta, dobbiamo interrompere la corda ai
due terzi e quindi, indicando con C la lunghezza della
sezione che produce questo nuovo suono, abbiamo A:C =
3:2. Infine, i suoni prodotti dalle corde C e B formano un
intervalli di quarta, e C:B = 4:3. Abbiamo quindi che le tre
consonanze principali, ottava quinta e quarta,
corrispondono ai rapporti 2:1; 3:2 e 4:3.
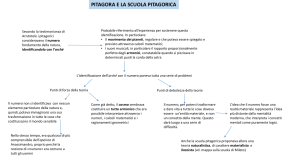
La crisi dei pitagorici
Per i pitagorici numero significava solo numero
intero perciò essi erano infastiditi dalla scoperta
che alcuni rapporti, come quello tra la diagonale
e il lato del quadrato non fossero esprimibili
mediante numeri interi.
I numeri irrazionali
Ippaso da Metaponto comprese per primo che il
valore esatto di questo numero non poteva essere
ricavato da una semplice formula e neppure da una
serie limitata di calcoli. Aveva in pratica scoperto
che esistevano grandezze incommensurabili. Oggi
sappiamo che i numeri irrazionali, come √2, sono
numeri che hanno una serie infinita e non
ripetitiva di cifre decimali.
non è in possibile dare un valore preciso di √2 ; si
tratta di una grandezza non misurabile con metodi
numerici.
In termini pratici ciò non comporta grandi
problemi, ma ha un significato teorico di enorme
portata.
La risoluzione passò attraverso il
famoso teorema di Pitagora sui
triangoli rettangoli
Come sappiamo, se a è l’ipotenusa e b e c sono i due cateti di un
triangolo rettangolo
Vale a2= b2+c2 (il quadrato costruito sull’ipotenusa è equivalente alla
somma dei quadrati costruiti sui due cateti).
Nel caso della diagonale del quadrato i due cateti sono uguali.
Applicando il teorema di Pitagora, si ha:
d2=l2+l2;
d2=2l2 ;
𝒅𝟐
𝒍𝟐
=2
𝒅
( 𝒍 )2 =2
Si tratta allora di determinare quel valore che elevato al quadrato dia
2.
𝒂 = 𝟐
Tale valore, come ben sappiamo, è
Conclusione:
• I numeri irrazionali sono quindi numeri,
facenti parte dell’insieme dei numeri reali, che
non possono essere scritti sotto forma di
frazione a/b con b diverso da 0 o numero
intero . Essi hanno dopo la “ , ” una
successione infinita di numeri che non si
ripetono.