Operazioni con le matrici
Algebra lineare
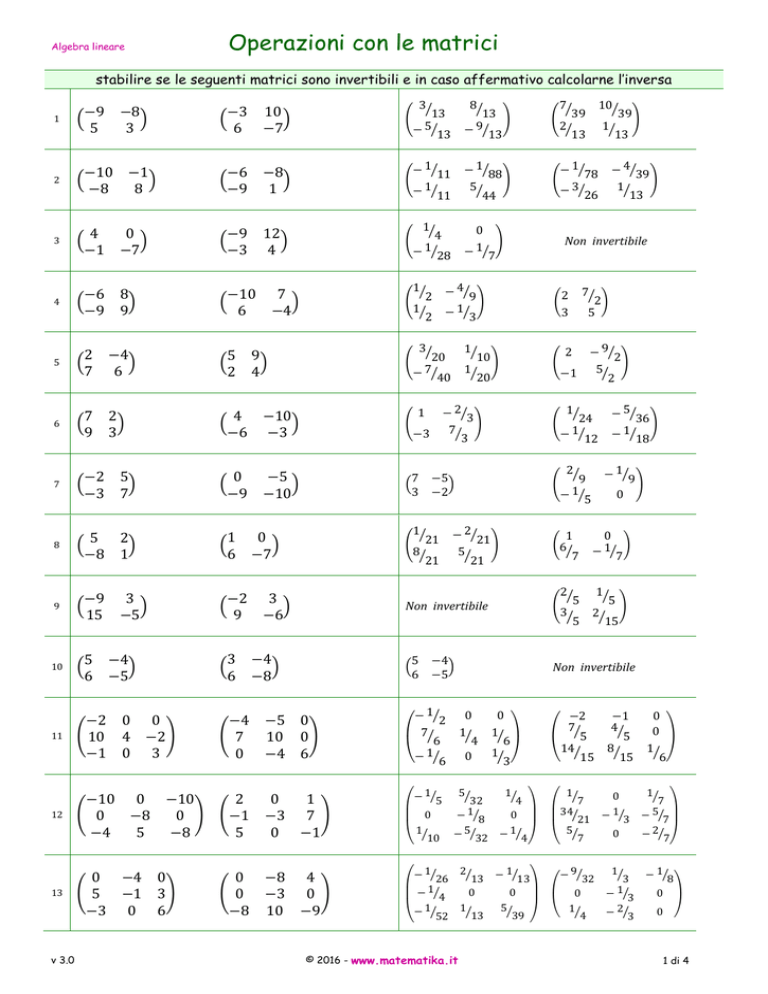
stabilire se le seguenti matrici sono invertibili e in caso affermativo calcolarne l’inversa
1
2
3
−9 −8
�
5
3
−3 10
�
6 −7
�
�
−10 −1
�
�
−8
8
−6 −8
�
�
−9 1
4
0
�
�
−1 −7
−6 8
�
−9 9
�
�
−9 12
�
�
−3 4
8�
13 �
9
− �13
1�
4
1
− �28
0
�
− 1�7
− 1�11
− 1�11
1�
� 2
1�
2
−10 7
�
6
−4
− 1�88
�
5�
44
− 4�9
�
− 1�3
4
�
5
�
6
�
7
�
8
�
9
�
10
�
�
−2 0 0
� 10 4 −2�
−1 0 3
−4 −5 0
� 7 10 0�
0 −4 6
− 1�2
⎛ 7�
6
1
⎝− �6
0 −4 0
� 5 −1 3�
−3 0 6
0 −8 4
� 0 −3 0 �
−8 10 −9
− 1�26 2�13 − 1�13
⎛ 1
⎞
0
0 ⎟
⎜ − �4
− 1�52 1�13 5�39
⎝
⎠
11
12
13
v 3.0
2 −4
�
7 6
7 2
�
9 3
−2 5
�
−3 7
5 2
�
−8 1
−9 3
�
15 −5
5 −4
�
6 −5
−10 0 −10
� 0
−8
0 �
−4
5
−8
�
�
3�
13
5
− �13
�
�
�
�
�
5 9
�
2 4
�
4 −10
�
−6 −3
�
0
−5
�
−9 −10
�
3�
20
− 7�40
− 2�3
�
7�
3
1
−3
7
3
−5
�
−2
1�
� 21
8�
21
1 0
�
6 −7
−2 3
�
9 −6
1�
10�
1�
20
− 2�21
�
5�
21
Non invertibile
3 −4
�
6 −8
�
2
0
1
�−1 −3 7 �
5
0 −1
5
6
−4
�
−5
− 1�5
⎛
⎜ 0
1�
⎝ 10
− 1�78
�
− 3�26
10�
39�
1�
13
− 4�39
�
1�
13
Non invertibile
�
2
3
2
�
−1
7�
2�
5
− 9�2
�
5�
2
1�
� 24
− 1�12
2�
� 9
− 1�5
1
�6
�7
2�
� 5
3�
5
− 5�36
�
− 1�18
− 1�9
0
�
0
�
− 1�7
1�
5�
2�
15
Non invertibile
0
0
1� 1� ⎞
4
6
1
0
�3⎠
5�
1�
4
32
⎞
− 1�8
0 ⎟
− 5�32 − 1�4
⎠
© 2016 - www.matematika.it
7�
� 39
2�
13
−2
7�
�
5
14�
15
−1
4�
5
8�
15
0
0 �
1�
6
1�
1�
0
7
7
⎛34
1� − 5� ⎞
�
−
⎜ 21
7⎟
3
5�
2�
0
−
7⎠
⎝ 7
⎛
− 9�32
0
1
⎝ �4
1�
1
3 − �8
− 1�3
0 ⎞
− 2�3
0 ⎠
1 di 4
Operazioni con le matrici
Algebra lineare
14
15
16
17
0 0
�6 1
0 0
−2
2�
7
9 4 0
�3 0 0 �
0 −4 3
3 −5 −10
�−8 0
2 �
3
0
3
2 1
0
�0 −4 −3�
0 −5 −1
−6 0 4
�−3 0 7�
−5 7 5
−10 0
0
� −9
0
0�
9
−3 10
0 −2
1 2�
5 0
0
⎛1�
4
1�
⎝ 3
1�
3
3
− �4
−1
0
0 ⎞
1�
3⎠
1�
0
− 1�10
15
⎛ 1
13
37� ⎞
−
−
−
�
�
⎜
5
50
75⎟
1�
4�
0
10
15
⎝
⎠
3�
1� − 1�
2
22
22
3
1�
⎛ 0
⎞
11 − �11
5
4�
⎝ 0 − �11
11 ⎠
− 5�4
⎛ 5
⎜ �6
4�
⎝ 3
3�
4
⎞
1
− �2⎟
− 2�3
5�
9
8�
9
−1
⎠
Non invertibile
1�
1�
1
18
18 − �90
⎛
1� ⎞
0
⎜ 0
5 ⎟
5
2
1
− �9 �18 − �18
⎝
⎠
calcolo i prodotti righe per colonne 𝑣𝑣𝑣𝑣 e 𝐴𝐴𝐴𝐴, rispettando l’orientamento dei vettori
18
𝑣𝑣 = (3 −6)
;
𝐴𝐴 = �
19
𝑣𝑣 = (−6 7)
;
𝐴𝐴 = �
20
𝑣𝑣 = (−9 −4)
;
𝐴𝐴 = �
21
𝑣𝑣 = (−6 9)
;
𝐴𝐴 = �
22
𝑣𝑣 = (4 −1)
;
𝐴𝐴 = �
23
𝑣𝑣 = (0 −5)
;
𝐴𝐴 = �
24
𝑣𝑣 = (7 0)
;
𝐴𝐴 = �
25
𝑣𝑣 = (−3 −5)
;
𝐴𝐴 = �
v 3.0
Non invertibile
−4 0 −3
�6 9 0�
0 8 −5
10
�8
0
− 7�30 2�15
0
⎛ 2
1
1 ⎞
⎜− �21 − �21 �7⎟
1�
− 1�10
0
5
⎝
⎠
7 0
�
4 −9
−3 1
�
0 10
0 −7
�
0 1
1 1
�
1 0
−1 9
�
10 0
6 4
�
−1 5
−4 4
�
0 1
−1 0
�
7 −7
© 2016 - www.matematika.it
(−3
54)
�
21
�
66
(18
64)
�
25
�
70
(0
59)
�
28
�
−4
(3
−6)
�
3
�
−6
(−14
(5
36)
−25)
(−28
28)
(−32
35)
�
−13
�
40
�
−20
�
−25
�
−28
�
0
�
3
�
14
2 di 4
Operazioni con le matrici
Algebra lineare
26
𝑣𝑣 = (0 6)
;
𝐴𝐴 = �
27
𝑣𝑣 = (−2 −2)
;
𝐴𝐴 = �
28
𝑣𝑣 = (−5 4
;
29
𝑣𝑣 = (7 −10
30
𝑣𝑣 = (10
31
𝑣𝑣 = (3 0
−7)
;
32
𝑣𝑣 = (9 2
−10)
;
33
𝑣𝑣 = (8 −1
−9)
;
9)
;
3 10)
;
𝐴𝐴 = (7 0
35
𝐴𝐴 = (10
36
𝐴𝐴 = (−1 6
38
v 3.0
0 5
�
8 −6
(−30
18)
�
−54
�
18
(−16
2)
�
−10
�
−4
−6 −1 −2
𝐴𝐴 = � 9 −6 −10�
4
0 −10
(82
0
−6 −5
𝐴𝐴 = � 10 −2 −8�
−10 −3 −6
(−70
3 −8 −2
𝐴𝐴 = � 0 −8 0 �
−2 −9 −9
−19
−6 −9
0
𝐴𝐴 = � 9
−8 −4�
0 −10 −1
(−132
7 1 −10
𝐴𝐴 = �8 10
3 �
0 −1 −7
(21
10
(47
2
−1 −3 −10
𝐴𝐴 = � 0 10
1 �
−8 −5
3
(64
11
18
�−109�
−60
−70)
−73
−96
31)
−134)
48
�107�
91
−68
� 14 �
−169
91
�3�
49
19)
31
�−16�
54
72)
85
�−19�
−86
−108)
date le matrici 𝐴𝐴 e 𝐵𝐵, calcola i prodotti righe per colonne 𝐴𝐴𝐴𝐴 e 𝐵𝐵𝐵𝐵
34
37
4)
0 −9
�
−5 3
1)
;
𝐵𝐵 = (6 5
−4 7)
;
𝐵𝐵 = (−7 −6 0)
4)
;
𝐵𝐵 = (8 0
−4
7
𝐴𝐴 = �−10 10�
0
8
;
0 0 −5
𝐵𝐵 = �
�
2 4 0
;
2 0
𝐵𝐵 = �
0 10
3 −9
𝐴𝐴 = �4 0 �
8 0
3)
3 1)
2
�
5
© 2016 - www.matematika.it
45
−46
Non è possibile calcolare i prodotti
(perchè?)
14
�20
16
6
�8
16
28
40
32
−90
0
0
20
50�
0
−39
8 �
16
�
0
−48
�
22
80
−40
�
54
−18
�
0
3 di 4
Algebra lineare
39
40
41
42
43
44
45
46
47
48
49
50
v 3.0
Operazioni con le matrici
0 2
𝐴𝐴 = �−1 7�
0 0
0 0
𝐴𝐴 = �−6 7�
6 0
0 −8
𝐴𝐴 = �9 0 �
0 −8
10 −5
𝐴𝐴 = � 5 −2�
8 −4
1 8
𝐴𝐴 = �0 10�
5 0
0 −1
𝐴𝐴 = �−4 −4�
0 −3
5
0
𝐴𝐴 = � 2 −3�
−1 0
1
2
𝐴𝐴 = �−7 0 �
−5 −3
9
0
1
−7
𝐴𝐴 = �
�
0
−7
−10 0
6 0 −4
𝐴𝐴 = �6 0 −5�
0 −5 −3
−10 0 10
𝐴𝐴 = � −4
4
4�
4
−4 0
10 0 −2
𝐴𝐴 = �−9 0
1�
−1 −6 6
4
�14
0
;
0 −8 6
𝐵𝐵 = �
�
2 9 0
;
0 −10 −3
𝐵𝐵 = �
�
−1 −1 10
;
−6 −5
0
𝐵𝐵 = �
�
0
2 −10
;
4 5 10
𝐵𝐵 = �
�
5 6 −9
;
0 7 4
𝐵𝐵 = �
�
−2 0 −4
;
3 0 0
𝐵𝐵 = �
�
7 0 −3
;
−6 −4 10
𝐵𝐵 = �
�
−3 0
0
;
0 7 −9
𝐵𝐵 = �
�
−3 8 0
;
1 2
0
𝐵𝐵 = �
�
8 −1 −2
9
−55
�
−56
−10
−6 8 0
𝐵𝐵 = �−2 10 0�
−6 6 3
0
� −8
−16
;
;
;
4
5 −7
𝐵𝐵 = �−7 0 −7�
5 −7 −8
5 −3 −2
𝐵𝐵 = �0 6
6�
0 10 0
© 2016 - www.matematika.it
0
�−7
0
0
�−54
0
15
�10
12
−16
�−20
0
−7
�−40
−21
−30
� −3
6
18
71
0
0
53
−60
−16
−45
−16
20
13
16
7
0
35
8
−9
−56
�
67
0
42
88 � �
66
−18
−70
�
−7
80
0�
80
145
68 �
116
−28
−40�
20
0 3
0 12�
0 9
−20
−8
4
−6
�0
9
23
−49
−59
4
�−1
20
58
65
21
50
�−45
−5
0
−6�
0
18
9
7
−20
−50
37
27
�
−45
18
48
�
80
�
145
8
−70
�
−1
�
20
−22
70
�
−16
�
0
0
−3
�
2
50
−48
20 � �
−15
−10
12
�
0
−4
−59
27
�
−6
−9
63 �
45
�
0
Non è possibile
14
� calcolare 𝐵𝐵𝐵𝐵
14
(perchè?)
0
−10
−2 �
59
−20
32
−8
�
30
12�
0
54
�−42
−12
28
�−20
48
−20
79
18 � �−60
−34
−90
35
35
40
32
40
12
12
−36
0
−20
49 �
39
−28
20 �
−36
−25
42 �
10
4 di 4












