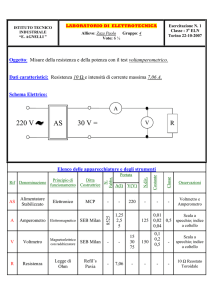
UNIVERSITA’ DEGLI STUDI DI TRENTO
SCUOLA DI SPECIALIZZAZIONE ALL’INSEGNAMENTO SECONDARIO
INDIRIZZO SCIENTIFICO MATEMATICO FISICO INFORMATICO
classe A049 matematica e fisica
Relazione di laboratorio
Caratteristica I-V
di una resistenza
Dott. Mario Sandri
Matricola 117039
Anno Accademico 2005/2006
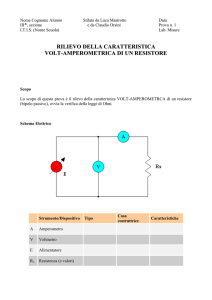
Caratteristica I-V di una resistenza
Mario Sandri
INDICE
Pagina 3
Scopo
Pagina 3
Materiali principali
Pagina 4
Richiami teorici
Pagina 5
Inserzione con amperometro a valle del voltmetro
Pagina 7
Inserzione con amperometro a monte del voltmetro
Pagina 9
Procedura
Pagina 12
Risultati
Pagina 12
Resistenza 1
Pagina 15
Resistenza 2
Pagina 19
Conclusioni
Pagina 2
Caratteristica I-V di una resistenza
Mario Sandri
SCOPO
Determinare il valore di due resistenze date misurandone la caratteristica I-V utilizzando sia
il metodo a valle e quello a monte, confrontando il valore del metodo che si ritiene più
appropriato con quelli ricavati dall’indice colori della resistenza e dall’ohmmetro. Valutare i
casi in cui si deve applicare il metodo a valle e quelli in cui si deve applicare il metodo a
monte.
MATERIALI PRINCIPALI
•
Generatore di tensione DC
•
Due Tester di classe 1
•
Due resistenze incognite
•
Breadboard
•
Cavi di collegamento
•
Carta millimetrata
Pagina 3
Caratteristica I-V di una resistenza
Mario Sandri
RICHIAMI TEORICI
La misura diretta di una resistenza viene effettuata per mezzo di un ohmmetro, ossia di uno
strumento appositamente dedicato a tale funzione. In pratica si usa un multimetro, digitale o
analogico, selezionando la funzione richiesta.
La misura diretta non è però molto precisa (nella maggior parte dei casi); maggiore accuratezza
si ottiene con il metodo volt-amperometrico, meno pratico e immediato di quello precedente. Con
tale metodo viene effettuata una misura indiretta della resistenza: il resistore in esame viene
alimentato da un apposito generatore e vengono misurati i valori di tensione e corrente; il rapporto
V/I fornisce il valore della resistenza incognita.
A seconda di come gli strumenti vengono collegati al resistore in prova si possono avere due tipi
di inserzione:
•
inserzione con amperometro a valle, in cui l’amperometro viene collegato direttamente in
serie al resistore e, quindi, il voltmetro si trova, con riferimento all’alimentazione, a monte
dell’amperometro;
•
inserzione con amperometro a monte, in cui il voltmetro viene collegato direttamente in
parallelo al resistore e, quindi, l’amperometro si trova, rispetto ai morsetti di alimentazione,
si trova a monte del voltmetro.
Ra
A
Rv
Rg
Rx
Vcc
Configurazione (a)
Amperometro a valle del Voltmetro
V
Ra
A
Rg
Vcc
Rv
Rx
Configurazione (b)
Amperometro a monte del Voltmetro
V
In entrambi i casi la misura è affetta da un errore sistematico d’inserzione, dovuto
all’autoconsumo degli strumenti, che si può valutare conoscendo le caratteristiche degli stessi.
Pagina 4
Caratteristica I-V di una resistenza
Mario Sandri
INSERZIONE CON AMPEROMETRO A VALLE DEL VOLTMETRO
In questo caso la tensione Vletta misurata dal voltmetro è pari alla somma della tensione Vvera del
resistore a della caduta di tensione dovuta alla resistenza RA interna all’amperometro, mentre la
corrente Iletta misurata dall’amperometro è esattamente uguale a quella assorbita dal resistore:
I vera = I letta
Vvera = Vletta − RA I letta
Il rapporto:
Rletta =
Vletta
I letta
Rappresenta la resistenza misurata, calcolata con i valori letti sui due strumenti, mentre il rapporto
Rx =
Vvera Vletta − RA I letta Vletta
=
=
− RA
I vera
I vera
I letta
Corrisponde al valore effettivo della resistenza incognita. Sostituendo Rletta nell’espressione
precedente si arriva alla seguente formula:
Rx = Rletto − RA
Dall’esame di quest’ultima relazione si possono trarre alcune conclusioni:
•
il valore della resistenza effettiva differisce da quello misurato a causa della resistenza
interna dell’amperometro;
•
al diminuire di RA rispetto a Rletta la differenza si riduce, fino ad annullarsi se RA assume un
valore teoricamente nullo;
•
l’errore assoluto commesso è positivo e pari a RA e quindi il valore di resistenza misurato
risulta maggiore di quello effettivo.
A risultati analoghi, ma maggiormente rigorosi, si arriva andando ad analizzare il comportamento di
una grandezza direttamente misurabile, in questo caso la tensione.
Pagina 5
Caratteristica I-V di una resistenza
Mario Sandri
Vvera = Vletta − RA I letta
L’errore assoluto commesso risulta essere pari a:
ε a = Vletta − Vvera = RA I letta
dunque positivo e quindi il valore misurato della tensione presenta un errore sistematico per eccesso
pari a:
εr =
Vletta − Vvera RA I letta RA
=
=
Vvera
Vvera
Rx
Tale errore deve essere inferiore alla risoluzione dello strumento, che nel caso di un tester di classe
1 corrisponde all’1% del fondo scala, cioè:
RA
< 0.01
Rx
da cui si deduce che tale errore può essere mascherato e dunque non considerato solo quando
RA < 0.01 Rx
In caso contrario bisogna apportare una correzione alla misura utilizzando le formule di partenza.
L’inserzione con amperometro a valle del voltmetro risulta pertanto conveniente per elevati valori
della resistenza misurata, tale da portare l’errore entro limiti accettabili.
Pagina 6
Caratteristica I-V di una resistenza
Mario Sandri
INSERZIONE CON AMPEROMETRO A MONTE DEL VOLTMETRO
In questo caso la tensione Vletta misurata dal voltmetro è esattamente pari alla tensione Vvera del
resistore, mentre la corrente Iletta misurata dall’amperometro è la somma della corrente Ivera assorbita
dal resistore e della corrente che passa nel ramo del voltmetro di resistenza RV:
Vvera = Vletta
I vera = I letta −
Vletta
RV
Il rapporto:
Rletta =
Vletta
I letta
Rappresenta la resistenza misurata, calcolata con i valori letti sui due strumenti, mentre il rapporto
Rx =
Vvera
Vvera
=
I vera I − Vletta
letta
RV
Corrisponde al valore effettivo della resistenza incognita. Sviluppando l’espressione precedente si
arriva alla seguente formula:
Rx =
Rletta
R
1 − letta
RV
Dall’esame di quest’ultima relazione si possono trarre alcune conclusioni:
•
il valore della resistenza effettiva differisce da quello misurato a causa della resistenza
interna del voltmetro;
•
all’aumentare di RV rispetto a Rletta la differenza si riduce, fino ad annullarsi se RV assume un
valore teoricamente infinito;
Pagina 7
Caratteristica I-V di una resistenza
•
Mario Sandri
l’errore assoluto commesso è negativo e pari a −
2
Rletta
e quindi il valore di resistenza
RV − Rletta
misurato risulta minore di quello effettivo.
A risultati analoghi, ma maggiormente rigorosi, si arriva andando ad analizzare il comportamento di
una grandezza direttamente misurabile, in questo caso la corrente elettrica.
I vera = I letta −
Vletta
RV
L’errore assoluto commesso risulta essere pari a:
ε a = I letta − I vera =
Vletta
RV
dunque positivo e quindi il valore misurato della tensione presenta un errore sistematico per eccesso
pari a:
εr =
I letta − I vera
V
R
= letta = x
I vera
RV I letta RV
Tale errore deve essere inferiore alla risoluzione dello strumento, che nel caso di un tester di classe
1 corrisponde all’1% del fondo scala, cioè:
Rx
< 0.01
RV
da cui si deduce che tale errore può essere mascherato e dunque non considerato solo quando
RV > 100 Rx
In caso contrario bisogna apportare una correzione alla misura utilizzando le formule di partenza.
L’inserzione con amperometro a monte del voltmetro risulta pertanto conveniente per piccoli valori
della resistenza incognita, tale da portare l’errore entro limiti accettabili.
Pagina 8
Caratteristica I-V di una resistenza
Mario Sandri
PROCEDURA
•
In principio ho preso rilevato il colore presente sulle resistenze per determinare il loro
valore. Ho calcolato l’errore assoluto su ogni resistenza utilizzando la formula:
σR =
σ R% R
100
dove σR è l’errore assoluto, σR% quello percentuale e R il valore della resistenza.
•
Ho determinato la massima tensione VMAX applicabile ai capi di ogni singola resistenza
utilizzando come valori sia quello dell’indice colori che dell’ohmmetro utilizzando la
seguente formula:
VMAX = P ⋅ R
Ricordo che le resistenze utilizzate presentano una potenza massima dissipabile pari a 0.25
W.
•
Ho costruito il circuito esposto nella figura sottostante. Nella configurazione (a)
l’amperometro è a valle del voltmetro, mentre in quella (b) l’amperometro è a monte del
voltmetro.
Pagina 9
Caratteristica I-V di una resistenza
Mario Sandri
Ra
A
Rv
Rg
Rx
Vcc
Configurazione (a)
Amperometro a valle del Voltmetro
V
Ra
A
Rg
Rv
Rx
Vcc
Configurazione (b)
Amperometro a monte del Voltmetro
V
Nel disegno Rg rappresenta la resistenza interna del generatore, che nell’esperienza non
viene considerata.
•
In base al valore della resistenza è stato utilizzato il circuito più indicato. Ricordo che
l’inserzione con amperometro a valle del voltmetro risulta conveniente per elevati valori
della resistenza misurata, mentre quella con amperometro a monte del voltmetro risulta
conveniente per piccoli valori della resistenza incognita.
•
Ho misurato la tensione e l’intensità di corrente per ognuna delle due resistenze a mia
disposizione e ho messo i dati in tabella. Nel caso della resistenza più piccola ho variato la
tensione tra circa 0 e 4 V con intervalli irregolari, mentre nel caso della resistenza più
grande ho variato la tensione tra circa 1 e 30 V con intervalli ancora irregolari.
•
Ho disegnato su carta millimetrata l’andamento della tensione in funzione della corrente
elettrica. Ho ricavato la pendenza che meglio interpreta i dati sperimentali e quelle di
pendenza massima e minima, con le quali è possibile ricavare l’errore sulla pendenza.
Pagina 10
Caratteristica I-V di una resistenza
•
Mario Sandri
Nella configurazione (a) l’amperometro misura la corrente Ix che scorre nella resistenza Rx,
mentre il voltmetro misura la somma delle cadute di potenziale su RA e su Rx, VA e Vx, cioè la
Vvera e la sua indeterminazione σV vera sono date dalle seguenti formule:
Vvera = Vletta − RA I letta
σ V vera = σ V letta + RA ⋅ σ I letta
•
Nella configurazione (b), invece, l’amperometro misura la corrente Ix che scorre nel
parallelo formato dalla resistenza Rx e dalla resistenza interna del Voltmetro RV. Il voltmetro
misura ora la caduta di potenziale solamente su Rx, cioè la Ivera e la sua indeterminazione σI
vera
sono date dalle seguenti formule:
I vera = I letta −
Vletta
RV
σ I vera = σ I letta +
σ V letta
RV
La sensibilità del Tester ICE 680R usato come voltmetro, è di 20000 Ohm per Volt di
fondoscala. Se il tester viene usato come Amperometro la sua resistenza interna deve essere
ricavata per ogni fondo scala dallo schema fornito dal costruttore. In tabella sono riportate le
portate e la relativa resistenza interna per il Tester ICE 680R.
•
Fondo scala
RA
50 µA
1500 Ω
500 µA
150 Ω
5 mA
15 Ω
50 mA
1.5 Ω
500 mA
0.15 Ω
5A
0.015 Ω
Dai valori di tensione e intensità di corrente, che nel caso a valle sono Vvera e Iletta, mentre in
quello a monte sono Vvera e Iletta, ho ricavato i corrispondenti valori della resistenza con la
sua indeterminazione utilizzando le seguenti formule:
Pagina 11
Caratteristica I-V di una resistenza
Mario Sandri
Vn
In
Rn =
⎛ σ nV σ nI ⎞
+
⎟ Rn
⎝ Vn I n ⎠
σ nR = ⎜
dove:
σ nR è l’indeterminazione sul valore n-esimo della resistenza Rn calcolata;
σ nV è l’indeterminazione sul valore n-esimo del voltaggio misurato;
σ nI è l’indeterminazione sul valore n-esimo dell’amperaggio misurato.
•
Dai valori delle resistenze ottenuti precedentemente, ho potuto ricavare la media R e la loro
indeterminazione σ R utilizzando le formule seguenti, dove N è il numero di misure
effettuate:
R=
σR =
•
∑R
n
n
N
∑(R
n
− R)
2
n
N −1
Infine ho confrontato la compatibilità percentuale C% tra il valore delle resistenze ottenute
con l’indice colori, con la procedura grafica e con la legge di Ohm utilizzando le seguenti
formule:
C% =
Rx − Ry
Rmedio
Rmedio =
100
Rx + Ry
2
dove x e y rappresentano due dei casi menzionati precedentemente.
Pagina 12
Caratteristica I-V di una resistenza
Mario Sandri
RISULTATI
Resistenza 1
La tabella mostra il valore della prima resistenza ottenuto con l’indice colori e con l’ohmmetro.
Indice colori
Rcolori
Colore
σR%colori
σRcolori
(Ω)
tolleranza
(%)
(Ω)
100
Oro
5
5
Marrone, nero, marrone
La tabella evidenzia la tensione massima applicabile ai capi della resistenza.
Vcolori
σVcolori
σV%colori
(V)
(V)
(%)
5.0
0.1
3
Per non rischiare di bruciare la resistenza, ho deciso di misurare tensioni massime pari a circa 4 V.
Dato il valore basso della resistenza si è deciso di utilizzare il metodo dell’amperometro a monte del
voltmetro. In tabella sono stati riportati i valori di tensione e intensità di corrente misurati.
V
σV
σV%
(V)
(V)
(%)
0,003
0,001
33
0,010
0,001
0,023
Fondo scala
Fondo scala
I
σI
σI%
(mA)
(mA)
(%)
0,1
0,0330
0,0005
2
0,05
10
0,1
0,110
0,005
5
0,5
0,001
4
0,1
0,250
0,005
2
0,5
0,040
0,001
3
0,1
0,420
0,005
1
0,5
0,093
0,001
1
0,1
1,00
0,05
5
5
0,22
0,02
9
2
2,20
0,05
2
5
1,00
0,02
2
2
10,0
0,5
5
50
1,60
0,02
1
2
16,0
0,5
3
50
1,80
0,02
1
2
18,0
0,5
3
50
2,3
0,1
4
10
23,0
0,5
2
50
4,0
0,1
3
10
41,0
0,5
1
50
voltmetro
(V)
Pagina 13
amperometro
(mA)
Caratteristica I-V di una resistenza
Mario Sandri
Dai dati in tabella è stato ricavato il grafico dell’andamento della tensione in funzione dell’intensità
di corrente.
4,5
4
3,5
Tensione (V)
3
2,5
2
1,5
1
0,5
0
0
5
10
15
20
25
30
35
40
45
Intensità corrente (mA)
Utilizzando una carta millimetrata è stato possibile trovare il valore della pendenza della retta e il
relativo errore. Tali valori rappresentano il valore della resistenza e la relativa indeterminazione. In
tale caso si è ottenuto il seguente valore:
R = 98.3 ± 0.5 Ω
L’errore percentuale è risultato essere dello 0,5 %.
In tabella sono stati riportati i valori dell’intensità di corrente vera e della resistenza calcolata per
ogni coppia di dati.
Pagina 14
Caratteristica I-V di una resistenza
Mario Sandri
V
σV
σV%
I vera
σI vera
σI% vera
R
σR
σR%
(V)
(V)
(%)
(mA)
(mA)
(%)
(Ω)
(Ω)
(%)
0,003
0,001
33
0,032
0,001
3
95
35
37
0,010
0,001
10
0,105
0,006
5
95
15
15
0,023
0,001
4
0,239
0,006
2
96
6
7
0,040
0,001
3
0,400
0,006
1
100
4
4
0,093
0,001
1
0,95
0,05
5
98
6
6
0,22
0,02
9
2,19
0,05
2
100
11
11
1,00
0,02
2
10,0
0,5
5
100
7
7
1,60
0,02
1
16,0
0,5
3
100
4
4
1,80
0,02
1
18,0
0,5
3
100
4
4
2,3
0,1
4
23,0
0,5
2
100
7
7
4,0
0,1
3
41,0
0,5
1
98
4
4
Dai dati in tabella è stato ricavato il valore medio e l’indeterminazione per la resistenza calcolata
con l’ausilio della legge di Ohm e ciò risulta essere pari a:
R = 98 ± 2 Ω
L’errore percentuale è risultato essere dello 2 %.
La tabella mostra le compatibilità tra le resistenze ottenute con i tre metodi distinti.
R
R
R
colori
pendenza
ohm
(Ω)
(Ω)
(Ω)
100
98.3
98
C%
C%
C%
colori-
colori-
pendenza-
pendenza
ohm
ohm
(%)
(%)
(%)
2
2
0.3
Pagina 15
Caratteristica I-V di una resistenza
Mario Sandri
Resistenza 2
La tabella mostra il valore della prima resistenza ottenuto con l’indice colori e con l’ohmmetro.
Indice colori
Rosso, rosso, giallo
Rcolori
Colore
σR%colori
σRcolori
(Ω)
tolleranza
(%)
(Ω)
220000
Oro
5
235
La tabella evidenzia la tensione massima applicabile ai capi della resistenza.
Vcolori
σVcolori
σV%colori
(V)
(V)
(%)
235
6
3
In questo caso non c’è possibilità di bruciare la resistenza in quanto l’alimentatore a disposizione
non raggiunge tensioni così elevate. Dato il valore alto della resistenza si è deciso di utilizzare il
metodo dell’amperometro a valle del voltmetro. In tabella sono stati riportati i valori di tensione e
intensità di corrente misurati.
V
σV
σV%
(V)
(V)
(%)
0,46
0,02
4
1,16
0,02
1,64
Fondo scala
Fondo scala
I
σI
σI%
(µA)
(µA)
(%)
2
2,0
0,5
25
50
2
2
5,0
0,5
10
50
0,02
1
2
7,0
0,5
7
50
3,3
0,1
3
10
14,0
0,5
4
50
6,3
0,1
2
10
27,0
0,5
2
50
8,4
0,1
1
10
36,0
0,5
1
50
10,7
0,5
5
50
46,0
0,5
1
50
20,0
0,5
3
50
90
5
6
500
30,8
0,5
2
50
140
5
4
500
voltmetro
(V)
Pagina 16
amperometro
(µA)
Caratteristica I-V di una resistenza
Mario Sandri
Dai dati in tabella è stato ricavato il grafico dell’andamento della tensione in funzione dell’intensità
di corrente.
35
30
Tensione (V)
25
20
15
10
5
0
0
20
40
60
80
100
120
140
160
Intensità corrente (microA)
Utilizzando una carta millimetrata è stato possibile trovare il valore della pendenza della retta e il
relativo errore. Tali valori rappresentano il valore della resistenza e la relativa indeterminazione. In
tale caso si è ottenuto il seguente valore:
R = 219617 ± 1690 Ω
L’errore percentuale è risultato essere dello 0,8 %.
In tabella sono stati riportati i valori dell’intensità di corrente vera e della resistenza calcolata per
ogni coppia di dati.
Pagina 17
Caratteristica I-V di una resistenza
Mario Sandri
Vvera
σV vera
σV% vera
I
σI
σI%
R
σR
σR%
(V)
(V)
(%)
(µA)
(µA)
(%)
(Ω)
(Ω)
(%)
0,43
0,03
6
2,0
0,5
25
215000
67500
31
1,09
0,03
3
5,0
0,5
10
217000
27200
13
1,54
0,03
2
7,0
0,5
7
219286
19592
9
3,1
0,1
3
14,0
0,5
4
220714
15561
7
5,9
0,1
2
27,0
0,5
2
218333
8025
4
7,9
0,1
1
36,0
0,5
1
218333
6019
3
10,0
0,5
5
46,0
0,5
1
217609
13398
6
19,9
0,5
3
90
5
6
220722
17901
8
30,6
0,5
2
140
5
4
218500
11429
5
Dai dati in tabella è stato ricavato il valore medio e l’indeterminazione per la resistenza calcolata
con l’ausilio della legge di Ohm e ciò risulta essere pari a:
R = 218389 ± 1792 Ω
L’errore percentuale è risultato essere dello 1 %.
La tabella mostra le compatibilità tra le resistenze ottenute con i tre metodi distinti.
R
R
R
colori
pendenza
ohm
(Ω)
(Ω)
(Ω)
220000
219617
218389
C%
C%
C%
colori-
colori-
pendenza-
pendenza
ohm
ohm
(%)
(%)
(%)
0.2
1
0.6
Pagina 18
Caratteristica I-V di una resistenza
Mario Sandri
CONCLUSIONI
L’esperienza ha rilevato come vi siano due possibili modi per misurare il valore di una
resistenza utilizzando la legge di Ohm. La diversità dei due sistemi di misura, configurazione a
valle e a monte, è connessa col fatto che ogni strumento, nel nostro caso amperometro e voltmetro,
presentano una resistenza interna. Ricordo che in tale esperienza si è trascurata la resistenza interna
del generatore.
Andando ad analizzare nello specifico i risultati ottenuti, si osserva come i risultati ricavati
dall’indice colori, dal metodo della pendenza e con la legge di ohm presentino una compatibilità di
massima del 2%. Nel caso della prima resistenza, quella di valore nominale pari a 100 Ω,
osserviamo come il valore ricavato con la configurazione a monte sia pressoché identico a quello
ricavato con la legge di ohm e con l’indice colori. Questa affermazione fa sicuramente ritenere che
il metodo adottato per misurare la resistenza in esame sia ottimale.
Analogo è il discorso per quanto riguarda la seconda resistenza, cioè quella di 220000 Ω. In
questo caso si è adottata la configurazione a valle e tale scelta è stata confermata dai valori di
compatibilità ottenuti utilizzando i tre metodi visti precedentemente.
In entrambi i casi, altre ad aver dimostrato quale sia il metodo migliore per misurare le
resistenze in esame, si osserva come i valori calcolati e tabulati siano compatibili entro la barra
d’errore. Questo significa che se non si ha la necessità di misurare con estrema precisione il valore
di una resistenza, questa può essere calcolata con una delle tre configurazioni precedenti.
Attenzione, questa affermazione non ha carattere universale in quanto dipende molto dal tester
usato (nel caso in esame si utilizzava un tester di classe 1). Infatti se utilizzassimo uno strumento
che presenta resistenze interne diverse sia per l’amperometro che per il voltmetro, tale ultima
affermazione potrebbe essere immediatamente smentita.
Le conclusioni qui trovate sperimentalmente avvalorano la correttezza dello studio scientifico
delle due configurazioni in esame. È difficile stabilire universalmente un valore di resistenza che
possa essere da spartiacque per le due configurazioni, in quanto, come già visto, tale valore dipende
in maniera significativa dal tipo di tester utilizzato. Riassumendo:
•
l’inserzione con amperometro a valle del voltmetro risulta pertanto conveniente per elevati
valori della resistenza misurata: RA < 0.01 Rx
•
l’inserzione con amperometro a monte del voltmetro risulta pertanto conveniente per piccoli
valori della resistenza incognita: RV > 100 Rx
Pagina 19