Il concetto di limite in Matematica - TED

Massimi e minimi con la derivata prima
pag. 1 di 6
Ricerca di massimi e minimi col metodo della derivata prima
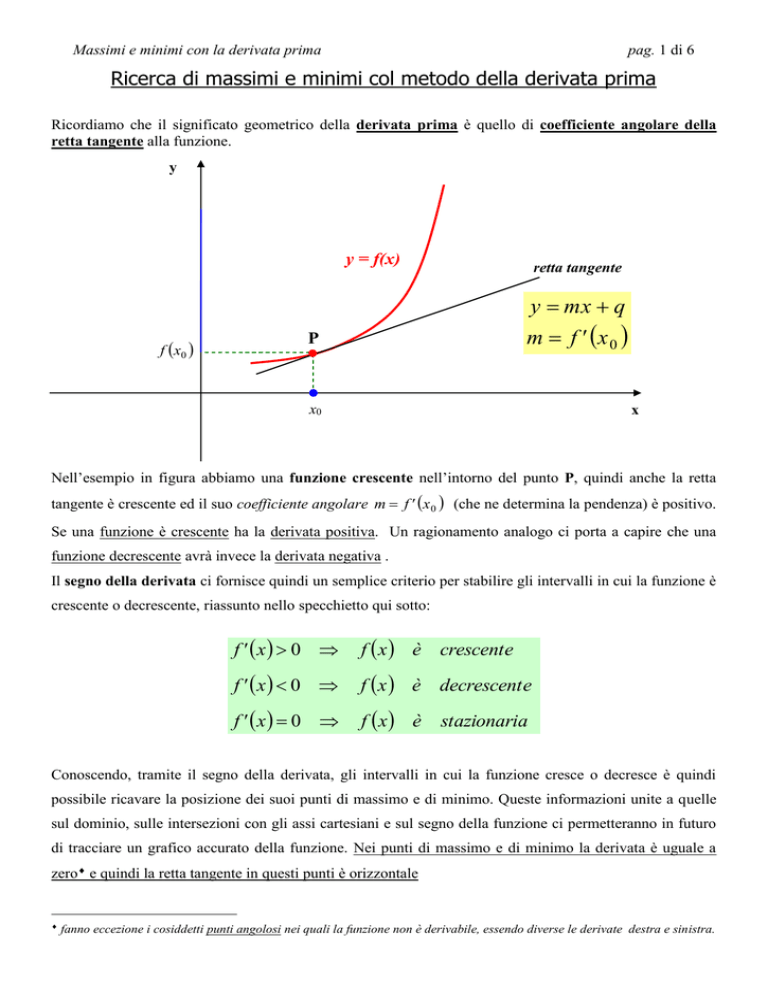
Ricordiamo che il significato geometrico della derivata prima è quello di coefficiente angolare della
retta tangente alla funzione.
y
y = f(x)
retta tangente
y  mx  q
f  x0 
m  f ' x 0 
P
x0
x
Nell’esempio in figura abbiamo una funzione crescente nell’intorno del punto P, quindi anche la retta
tangente è crescente ed il suo coefficiente angolare m  f ' x 0  (che ne determina la pendenza) è positivo.
Se una funzione è crescente ha la derivata positiva. Un ragionamento analogo ci porta a capire che una
funzione decrescente avrà invece la derivata negativa .
Il segno della derivata ci fornisce quindi un semplice criterio per stabilire gli intervalli in cui la funzione è
crescente o decrescente, riassunto nello specchietto qui sotto:
f ' x   0 
f x  è crescente
f ' x   0 
f x  è decrescent e
f ' x   0 
f x  è stazionaria
Conoscendo, tramite il segno della derivata, gli intervalli in cui la funzione cresce o decresce è quindi
possibile ricavare la posizione dei suoi punti di massimo e di minimo. Queste informazioni unite a quelle
sul dominio, sulle intersezioni con gli assi cartesiani e sul segno della funzione ci permetteranno in futuro
di tracciare un grafico accurato della funzione. Nei punti di massimo e di minimo la derivata è uguale a
zero e quindi la retta tangente in questi punti è orizzontale

fanno eccezione i cosiddetti punti angolosi nei quali la funzione non è derivabile, essendo diverse le derivate destra e sinistra.
Massimi e minimi con la derivata prima
pag. 2 di 6
I punti in cui f ' x   0 sono particolarmente interessanti perché in essi la funzione può avere un punto di
massimo , un punto di minimo o un punto di flesso a tangente orizzontale. I casi possibili sono
rappresentati qui sotto.
f ' x   0
In figura è rappresentato un punto di massimo relativo.
f ' x   0
f ' x   0
 La retta tangente in tale punto è orizzontale
 Il segno della derivata prima passa da positivo (funzione
crescente) a negativo (funzione decrescente).
………………………………………………………………………………………………………………...
In figura è rappresentato un punto di minimo relativo.
f ' x   0
f ' x   0
f ' x   0
 La retta tangente in tale punto è orizzontale
 Il segno della derivata prima passa da negativo (funzione
decrescente) a positivo (funzione crescente).
………………………………………………………………………………………………………………...
f ' x   0
f ' x   0
In figura è rappresentato un punto di flesso ascendente.
 La retta tangente in tale punto è orizzontale
 Il segno della derivata prima è positivo prima e dopo il
flesso
f ' x   0
………………………………………………………………………………………………………………...
In figura è rappresentato un punto di flesso discendente.
f ' x   0
f ' x   0
 La retta tangente in tale punto è orizzontale
f ' x   0
 Il segno della derivata prima è negativo prima e dopo il
flesso
………………………………………………………………………………………………………………...
È anche importante sottolineare che:
 nei punti di massimo la concavità della funzione è rivolta verso il basso
 nei punti di minimo la concavità della funzione è rivolta verso l’alto
 nei punti di flesso la concavità della funzione cambia da sinistra a destra
………………………………………………………………………………………………………………...
Massimi e minimi con la derivata prima
pag. 3 di 6
A questo punto siamo in grado di trovare i punti di massimo e di minimo di una funzione y  f x 
seguendo il procedimento descritto qui sotto:
1. determinazione del dominio della funzione
2. calcolo della derivata f ' x 
3. studio del segno della derivata risolvendo la disequazione f ' x   0
4. schema grafico in cui si determinano i punti di max e di minimo in base al segno di f ' x 
……………………………………………………………………………………………………………….
Esempio 1 : trovare i punti di massimo e di minimo della funzione y  4 x 3  18 x 2  24 x
1. Il dominio della funzione è D    ;  
f '  x   12 x 2  36 x  24
2. calcolo della derivata :
3. studio del segno della derivata : 12 x 2  36x  24  0 che diventa x 2  3x  2  0
La disequazione è di 2° grado e si risolve col metodo della parabola.
x1  1
 3 9 8 31
con la parabola abbiamo quindi:
x1,2 


2
2
x2  2
x 1 
x2
4. schema grafico col segno della derivata

segno di
1


crescente
decrescente
f ' x 
comportamento di
f x 

2

crescente
è evidente dallo schema grafico che in x  1 abbiamo un punto di massimo, mentre in x  2 abbiamo un
punto di minimo. L’ordinata dei due punti si calcola inserendo nella funzione y  f x  i valori
dell’ascissa.
1. Punto di massimo

 x 1

3
2

 y  f 1  4  1  18  1  24  1  4  18  24  10
il punto di massimo è il punto A1; 10
2. Punto di minimo

x2

3
2

 y  f 2   4  2   18  2   24  2  32  72  48  8
il punto di minimo è il punto B2 ; 8
Nella pagina seguente è riportato, in scala diversa sui due assi cartesiani, il grafico della funzione con
evidenziati i punti di massimo e di minimo.
Massimi e minimi con la derivata prima
pag. 4 di 6
A1; 10
B2 ; 8
Grafico della funzione y  4 x 3  18 x 2  24 x con evidenziati i due punti di massimo e di minimo.
……………………………………………………………………………………………………………….
Massimi e minimi con la derivata prima
pag. 5 di 6
Esempio 2 : trovare i punti di massimo e di minimo della funzione y  x 3  6 x 2  12 x  4
1. Il dominio della funzione è D    ;  
2. calcolo della derivata :
f ' x   3x 2  12 x  12
3. studio del segno della derivata : 3x 2  12 x  12  0 che diventa
x 2  4x  4  0
La disequazione è di 2° grado e si risolve col metodo della parabola. Con formula ridotta:
x1  2
2 44
x1,2 
20
1
x2  2
le soluzioni sono coincidenti e con la parabola abbiamo quindi:
x2 
x2
4. schema grafico col segno della derivata

segno di
f ' x 
comportamento di
f x 

2


crescente
crescente
La funzione risulta sempre crescente, non ha quindi né massimi né minimi.
Però questa volta in x  2 abbiamo un punto di flesso ascendente.
3. Punto di flesso
x2

x2

3
2

 y  f 2   2   6  2  12  2  4  8  24  24  4  4
il punto di flesso è il punto B2 ; 4
Qui sotto è riportato, in scala diversa sui due assi cartesiani, il grafico della funzione.
B2 ; 4
Massimi e minimi con la derivata prima
pag. 6 di 6
Esempio 3 : trovare i punti di massimo e di minimo della funzione y  3x 4  8 x 3  6 x 2  24 x
1. Il dominio della funzione è D    ;  
f '  x   12 x 3  24 x 2  12 x  24
2. calcolo della derivata :
3. studio del segno della derivata : 12 x 3  24 x 2  12 x  24  0 che diventa x 3  2 x 2  x  2  0
La disequazione si risolve scomponendo in fattori e confrontando i segni dei vari fattori
x 3  2 x 2  x  2  0  x 2  x  2   1   x  2   0  x  2   x 2  1  0 e quindi:
x  2  x  1  x  1  0
o segno del 1° fattore: x  2  0  x  2
o segno del 2° fattore: x  1  0  x  1
o segno del 2° fattore: x  1  0  x  1


4. schema grafico col segno della derivata

1° fattore
2° fattore
3° fattore
segno di
f ' x 
1




decrescente




1
crescente




decrescente
2





crescente
comportamento di
f x 
è evidente dallo schema grafico che in x  1 abbiamo un punto di massimo, mentre in x  1 e x  2
abbiamo due punti di minimo. L’ordinata dei tre punti si calcola inserendo nella funzione y  f x  i valori
dell’ascissa.
 1° punto di minimo

 x  1


 y  f  1  3  8  6  24  19
il 1° punto di minimo è il punto B 1 ;  19
 Punto di massimo

 x 1


 y  f 1  3  8  6  24  13
il punto di massimo è il punto A1; 13
 2° punto di minimo

x2

4
3
2

 y  f 2   3  2  8  2  6  2  24  2  48  64  24  48  8
il 2° punto di minimo è il punto C 2 ; 8