Raffreddamento e Riscaldamento di sostanze: quali

Raffreddamento e Riscaldamento di sostanze: quali meccanismi sono possibili?
Per riscaldare una sostanza occorre fornire una certa quantità di
calore; la quantità di calore da fornire per aumentare di un grado
centigrado un grammo di una data sostanza dipende dalle proprietà
caratteristiche della sostanza.
Tale quantità è denominata calore specifico, abitualmente misurato
in cal g-1K-1.
Per riscaldare una sostanza occorre spendere energia (per es. energia elettrica di un fornello a
piastra, energia chimica da combustione di un gas). Il nostro obiettivo è adesso quello di cercare di
costruire un modello che riesca a spiegare i meccanismi con cui avvengono i processi di
riscaldamento o raffreddamento in relazione alle energie fornite o sottratte.
1) Se riscaldiamo dello stesso ∆T masse uguali di due gas aventi calore
specifico diverso (possiamo pensare di averli posti in contenitori uguali) ci
accorgiamo che occorre fornire quantità di calore diverse. Ciò significa che
occorre tenere sullo stesso fornello i due gas per tempi diversi e quindi
fornire energie diverse. Come puoi spiegare questo fatto sperimentale?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
_______________________________________________________________
2. Quali pensi che possano essere le proprietà dei due gas in questione che influenzano questi
tempi diversi? (dai una breve descrizione dal punto di vista microscopico).
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
_______________________________________________________________________________
3. Considera adesso due solidi di calore specifico diverso; anche in questo caso per riscaldare due
masse uguali dello stesso incremento di temperatura ∆T, occorre fornire quantità di calore
diverse. Descrivi quale può essere a tuo avviso un semplice modello di solido capace di spiegare
questo risultato sperimentale. Indica, possibilmente con qualche dettaglio, cosa accade agli
atomi del solido al variare della temperatura e come questo può essere spiegato da un punto di
vista energetico.
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
_______________________________________________________________________________
________________________________________________________________________________
_______________________________________________________________________________
1
4. Cosa pensi possa differenziare due solidi con calore specifico diverso? Spiega come i diversi
calori specifici possano essere messi in relazione al modello di solido che hai ipotizzato in 3.
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
_______________________________________________________________________________
5. Pensa adesso ad un liquido e cerca di spiegare, alla luce di un modello microscopico, come si
comportano due liquidi con diverso calore specifico, quando la loro temperatura cresce dello
stesso intervallo ∆T.
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
_______________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
_______________________________________________________________________________
2
NOTE ESPLICATIVE
Nota 1
Calori specifici dei gas
I calori specifici dei gas vengono espressi generalmente come calori specifici molari. Nel caso di
gas perfetto monoatomico, l’energia interna è tutta di tipo cinetico e la teoria cinetica dei gas mette
a disposizione l’espressione analitica per questa forma di energia:
U = nN A KEavg = nN A
3
3
KT = nRT
2
2
Per i gas vengono definiti due tipi di calore molare, uno per le trasformazione a volume costante,
CV, l’altro per quelle a pressione costante, CP. Nel caso di una trasformazione effettuata da un gas
perfetto monoatomico a volume costante, dalla prima legge della termodinamica si ha:
Q = CV n∆T
Q = ∆U + P ∆V
CV =
1 ∆U 3
= R
n ∆T 2
Sviluppando ulteriormente la prima legge della termodinamica e l’equazione dei gas perfetti, si
ottiene, inoltre, la relazione
CP = CV + R
Calore specifico a volume costante
Il calore specifico molare a volume costante è definito come:
Q = nCV ∆T
Applicando la prima legge della termodinamica ad una trasformazione con V = costante si ha:
∆U + P∆V = nCV ∆T
ma ∆V = 0, quindi l’espressione per CV diventa CV =
Per un gas ideale monoatomico, U =
1 ∆U
n ∆T
3
3
J
nRT , quindi CV = R = 12,5
2
mol ⋅ K
2
Questo valore è in buon accordo con i risultati sperimentali ottenuti con gas nobili monoatomici
come l’elio e l’argon ma non descrive bene il comportamento dei gas bi o poli-atomici, poiché in
questi vi è un contributo al calore specifico dovuto a moti rotazionali e vibrazionali. Il teorema di
equipartizione dell’energia porta a:
U=
f
f
nRT e CV = R , dove f è il numero di gradi di libertà nel moto
2
2
molecolare
3
Nota 2: La legge di Dulong e Petit
Il calore specifico del rame è 0,093 cal/g °C (0,389 J/g °C) e quello del piombo solo 0,031 cal/g °C
(0,13 J/g °C). Come mai questi due valori sono così differenti?
Ciò è dovuto principalmente che questi valori di calore specifico sono espressi in termini di energia
per unità di massa; se li si fosse espressi come energia per mole essi sarebbero stati molto simili. La
similarità dei calori specifici molari dei solidi è l’argomento di cui tratta la legge di Dulong e Petit e
può essere spiegata considerando l’equipartizione dell’energia per gli atomi dei solidi.
Considerando solo i gradi di libertà traslazionali, si ottiene una energia di 3KT/2 per atomo. Nel
caso dei solidi, però, bisogna considerare il fatto che le vibrazioni atomiche forniscono tre gradi di
libertà aggiuntivi e portano l’energia totale per atomo a 3KT. Il calore specifico a volume costante è
definito come la rapidità di variazione dell’energia rispetto alla temperatura (la derivata rispetto alla
temperatura). Da cui si ha:
K = costante di Boltzmann
Energia per mole = 3KTNA
T = temperatura in Kelvin
NA = numero di Avogadro
∂
1
J
= 24,94
(3KTN A ) = 3KN A
∂T
mole
mol
Legge di Dulong e Petit:
Se li si considera su base molare, quindi, i calori specifici di rame e piombo risultano essere
abbastanza simili:
Rame. 0,386
J
g
J
× 63, 6
= 24, 6
g °C
mol
mole°C
Piombo. 0,126
J
g
J
× 207
= 26,5
g °C
mol
mole°C
Scostamenti dalla legge di Dulong e Petit
Energia per mole = 3KTNA
Legge di Dulong e Petit:
K = costante di Boltzmann
T = temperatura in Kelvin
NA = numero di Avogadro
∂
1
J
= 24,94
(3KTN A ) = 3KN A
∂T
mole
mol
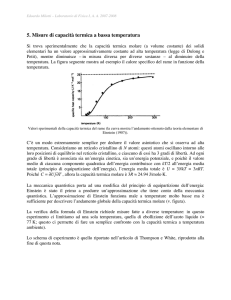
La legge di Dulong e Petit,
comunque, è basata sulla statistica
di Maxwell-Boltzmann e per
temperature basse si deve usare la
meccanica quantistica per ottenere
risultati in accordo con l’esperienza
La spiegazione del drastico scostamento dalla legge di Dulong e Petit è dovuto a Einstein e
Debye.
4
5