Il I principio della Termodinamica e le trasformazioni

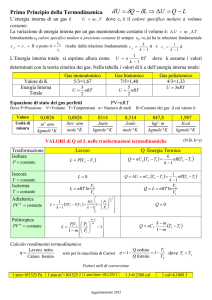
Il I principio della Termodinamica e le trasformazioni termodinamiche
-
-
-
Premesse
Equazione di stato dei gas perfetti:
PV = nRT
Ricordare che la temperatura va espressa sempre rigorosamente in kelvin, la pressione in pascal
e il volume in metri cubi.
3
L'energia interna di un gas monoatomico (elio, neon, argon, kripton o xenon) vale nRT ,
2
5
mentre per un gas biatomico è nRT . Quindi in qualsiasi esercizio sia richiesto il calcolo della
2
variazione di energia interna U, è possibile, noti i valori di n e la T iniziale e finale, calcolare
Ufinale - Uiniziale (ciò vale, ovviamente, per tutte le trasformazioni termodinamiche).
-
Calori specifici dei gas: mentre un solido e un liquido possono essere riscaldati in un solo modo
(Q = nC·T , dove C esprime il calore specifico molare, e T può essere espressa
indifferentemente in kelvin o in gradi Celsius), i gas possono essere riscaldati in infiniti modi
diversi. Fra questi, due sono i più semplici:
a) a volume costante: Q = nCV·T dove CV è la capacità termica molare a volume costante,
3
5
che vale R per i gas monoatomici e R per i gas biatomici.
2
2
b) A pressione costante: Q = nCP·T dove CP è la capacità termica molare a pressione
5
7
costante, che vale R per i gas monoatomici e R per i gas biatomici. I valori a pressione
2
2
costante sono più alti perché oltre a scaldare il gas si compie un lavoro (positivo) di
espansione del gas.
-
Un gas che varia il suo volume compie un lavoro (positivo se si espande, negativo se viene
compresso). Il lavoro si calcola come P·V, e quindi, ovviamente, può essere calcolato in
maniera elementare solo se P è costante (vedi oltre, trasformazione isobara).
-
TRASFORMAZIONI TERMODINAMICHE
a) Trasformazione isocòra o isovolumica (a volume costante).
Essendo V costante, non viene compiuto alcun lavoro (L = 0).
Quindi U = Q ; ma Q , a volume costante, è nCV·T (vedi prima, calori specifici dei gas).
b) Trasformazione isobara (a pressione costante).
Q = nCP·T (vedi sopra, calori specifici dei gas), e L = P·V. Quindi U = nCP·T - P·V.
c) Trasformazione isoterma (a temperatura costante).
Essendo T costante, l'energia interna, che dipende solo dalla temperatura, non varia. Quindi
risulta U = Q - L = 0 . Perciò Q = L. I valori di Q e di L si calcolano con un integrale, e sono
sempre uguali, in modulo e in segno.
d) Trasformazione adiabatica (senza scambi di calore con l'esterno).
Essendo Q = 0 , risulta U = - L. Non siamo in grado di calcolare L direttamente; se sono noti
il valore iniziale e finale di T, è possibile calcolare U e da esso dedurre L.