Principi di Kirchhoff – esercizio n. 11
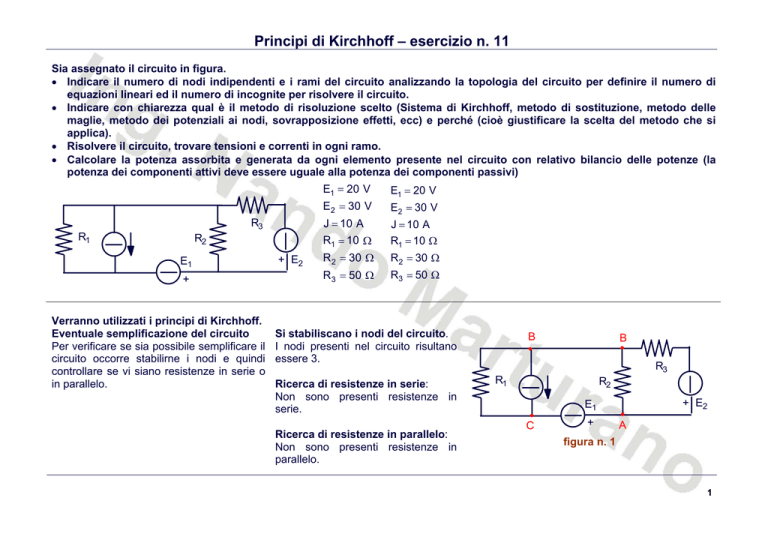
Sia assegnato il circuito in figura.
• Indicare il numero di nodi indipendenti e i rami del circuito analizzando la topologia del circuito per definire il numero di
equazioni lineari ed il numero di incognite per risolvere il circuito.
• Indicare con chiarezza qual è il metodo di risoluzione scelto (Sistema di Kirchhoff, metodo di sostituzione, metodo delle
maglie, metodo dei potenziali ai nodi, sovrapposizione effetti, ecc) e perché (cioè giustificare la scelta del metodo che si
applica).
• Risolvere il circuito, trovare tensioni e correnti in ogni ramo.
• Calcolare la potenza assorbita e generata da ogni elemento presente nel circuito con relativo bilancio delle potenze (la
potenza dei componenti attivi deve essere uguale alla potenza dei componenti passivi)
R3
R1
R2
E1
+
Verranno utilizzati i principi di Kirchhoff.
Eventuale semplificazione del circuito
Per verificare se sia possibile semplificare il
circuito occorre stabilirne i nodi e quindi
controllare se vi siano resistenze in serie o
in parallelo.
+ E2
E1 = 20 V
E1 = 20 V
E2 = 30 V
E2 = 30 V
J = 10 A
J = 10 A
R1 = 10 Ω
R1 = 10 Ω
R 2 = 30 Ω
R2 = 30 Ω
R 3 = 50 Ω
R3 = 50 Ω
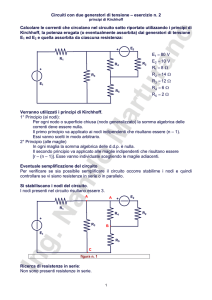
Si stabiliscano i nodi del circuito.
I nodi presenti nel circuito risultano
essere 3.
Ricerca di resistenze in serie:
Non sono presenti resistenze in
serie.
Ricerca di resistenze in parallelo:
Non sono presenti resistenze in
parallelo.
B
B
R3
R1
R2
+ E2
E1
C
+
A
figura n. 1
1
Principi di Kirchhoff – esercizio n. 11
1° Principio (ai nodi):
Per ogni nodo o superficie chiusa (nodo generalizzato) la somma algebrica delle correnti deve essere nulla.
Il primo principio va applicato ai nodi indipendenti che risultano essere (n – 1).
Essi vanno scelti in modo arbitrario.
2° Principio (alle maglie)
In ogni maglia la somma algebrica delle d.d.p. è nulla.
Il secondo principio va applicato alle maglie indipendenti che risultano essere
[r – (n – 1)].
Esse vanno individuate scegliendo le maglie adiacenti.
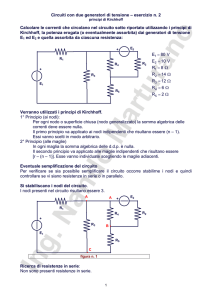
Si stabiliscano i nodi, i nodi indipendenti, i
rami e le maglie indipendenti del circuito.
In tale circuito si individuano
n = 3 nodi
(n – 1) = (3 – 1) = 2 nodi indipendenti
r = 5 rami
[r – (n – 1)] = [5 – (3 – 1)] = 3 maglie indipendenti
Si disegnino, come in figura 2, in
modo arbitrario, le correnti di ramo
che pur essendo 5 perchè tanti
sono i rami, risulteranno essere
incognite solo in 4, in quanto su di
un ramo è presente un generatore
di corrente di valori noti J.
(come maglie indipendenti verranno scelte quelle
Tuttavia, in contemporanea, è
adiacenti).
sconosciuta la d.d.p VCB ai capi del
generatore di corrente, che
costituisce
dunque
ulteriore
incognita nelle equazioni alle
maglie
che
saranno
successivamente scritte.
B
B
I1
+
J
R1
R3
+
R2
I0
VCB
+
I2
E1
C
+
I3
+ E2
A
figura n. 2
2
Principi di Kirchhoff – esercizio n. 11
Si ricorda che per applicare il secondo principio di Equazioni ai nodi indipendenti:
Kirchhoff occorre fissare un verso arbitrario
positivo di percorrenza della maglia.
nodo A: I0 = I2 + I3
nodo C: J = I0 + I1
I principi di Kirchhoff danno origine alle seguenti
equazioni:
Sostituendo i valori:
Risolvendo
il
sistema
si
determinano le correnti e le
d.d.p. incognite:
I0 = I2 + I3
87
143
10 = I0 + I1
I0 =
A ; I1 =
A
23
23
30 ⋅ I2 − 50 ⋅ I3 = 30
63
24
I2 =
A ; I3 =
A
−30 ⋅ I2 = −20 − VCB
23
23
10 ⋅ I1 = VCB
1430
VCB =
V
23
Calcolo della potenza erogata dai generatori:
Equazioni alle maglie indipendenti
R2 ⋅ I2 − R3 ⋅ I3 = E2
− R 2 ⋅ I2 = −E1 − VCB
R1 ⋅ I1 = VCB
maglia ABA
maglia ABBCA
maglia CBC
B
B
I1
R3
J
R1
R2
I0
VCB
I3
I2
E1
C
+
+ E2
A
figura n. 3
Calcolo delle potenze assorbite dalle resistenze;
2
Per calcolare la potenza fornita dai generatori di corrente occorre la d.d.p. VCB.
204490
⎛ 143 ⎞
2
=
⋅
=
⋅
P
R
I
10
W
1430
R1
1 1
⎜
⎟ =
529
VCB =
V
⎝ 23 ⎠
23
2
Poiché, per il generatore di tensione E2 il verso della corrente ed il verso P = R ⋅ I 2 = 30 ⋅ ⎛ 63 ⎞ = 119070 W
R2
2
2
⎜
⎟
della d.d.p. ai morsetti dei generatori sono discordi, allora tale generatore
529
⎝ 23 ⎠
assorbe potenza invece che erogarla e pertanto la sua potenza deve
2
28800
⎛ 24 ⎞
essere considera negativa.
PR3 = R3 ⋅ I3 2 = 50 ⋅ ⎜
W
⎟ =
529
⎝ 23 ⎠
3
Principi di Kirchhoff – esercizio n. 11
Verifica potenze erogate ed assorbite:
87 1740
W
=
23
23
24
720
PE2 = −E2 ⋅ I3 = −30 ⋅
W
=−
23
23
1430
14300
PJ = VCB ⋅ J =
⋅ 10 =
W
23
23
PE1 = E1 ⋅ I0 = 20 ⋅
14300 1740 720 15320
W
+
−
=
23
23
23
23
204490 119070 28800 15320
PRT = PR1 + PR2 + PR3 =
+
+
=
W
529
529
529
23
PET = PJ + PE1 + PE2 =
Soluzione sistema:
⎧I0 = I2 + I3
⎪
⎪⎪10 = I0 + I1
⎨30 ⋅ I2 − 50 ⋅ I3 = 30
⎪−30 ⋅ I = −20 − V
2
CB
⎪
⎪⎩10 ⋅ I1 = VCB
⇒
⎧I0 = I2 + I3
⎪
⎪⎪10 = I2 + I3 + I1
⎨3 ⋅ I2 − 5 ⋅ I3 = 3 ⇒
⎪30 ⋅ I = 20 + V
2
CB
⎪
⎪⎩10 ⋅ I1 = VCB
⎧10 = I2 + I3 + I1
⎪
⎪⎪3 ⋅ I2 − 5 ⋅ I3 = 3
⎨30 ⋅ I2 = 20 + VCB
⎪
⎪I1 = VCB
⎪⎩
10
VCB
⎧
⎪10 = I2 + I3 + 10
⎪
3 + 5 ⋅ I3
⎪
⇒ ⎨I2 =
3
⎪
⎪30 ⋅ I2 = 20 + VCB
⎪
⎩
⇒
3 + 5 ⋅ I3
V
⎧
+ I3 + CB
⎪⎪10 =
3
10
⎨
⎪30 ⋅ 3 + 5 ⋅ I3 = 20 + V
CB
⎪⎩
3
⇒
⎧ 27 − 8 ⋅ I3 VCB
=
⎪
⇒
3
10
⎨
⎪30 + 50 ⋅ I = 20 + V
3
CB
⎩
⎧270 − 80 ⋅ I3 = 3 ⋅ VCB
−10 + VCB
⎧
⎪
⇒ ⎨270 − 80 ⋅
= 3 ⋅ VCB ⇒ {1350 + 80 = 8 ⋅ VCB + 15 ⋅ VCB ⇒
−10 + VCB
⎨
50
I
=
⎩
⎪⎩ 3
50
1430
⇒ VCB =
23 ⋅ VCB = 1430
V
23
1430
24
1430
−10 +
3 +5⋅
−10 + VCB
23 = 24 A ; I = 3 + 5 ⋅ I3 =
23 = 63 A ; I = VCB = 23 = 143 A ; I = I + I = 63 + 24 = 87 A
=
I3 =
2
1
0
2
3
50
50
23
3
3
23
10
10
23
23 23 23
4