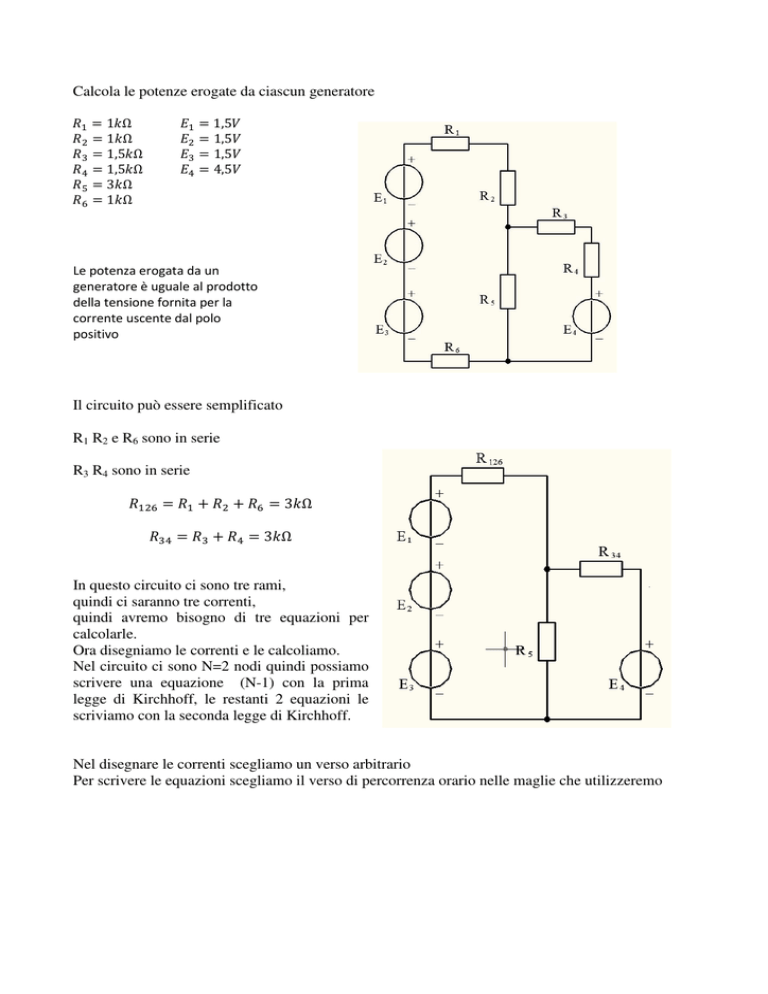
Calcola le potenze erogate da ciascun generatore
ܴଵ = 1݇Ω
ܴଶ = 1݇Ω
ܴଷ = 1,5݇Ω
ܴସ = 1,5݇Ω
ܴହ = 3݇Ω
ܴ = 1݇Ω
ܧଵ = 1,5ܸ
ܧଶ = 1,5ܸ
ܧଷ = 1,5ܸ
ܧସ = 4,5ܸ
Le potenza erogata da un
generatore è uguale al prodotto
della tensione fornita per la
corrente uscente dal polo
positivo
Il circuito può essere semplificato
R1 R2 e R6 sono in serie
R3 R4 sono in serie
ܴଵଶ = ܴଵ + ܴଶ + ܴ = 3݇Ω
ܴଷସ = ܴଷ + ܴସ = 3݇Ω
In questo circuito ci sono tre rami,
quindi ci saranno tre correnti,
quindi avremo bisogno di tre equazioni per
calcolarle.
Ora disegniamo le correnti e le calcoliamo.
Nel circuito ci sono N=2 nodi quindi possiamo
scrivere una equazione (N-1) con la prima
legge di Kirchhoff, le restanti 2 equazioni le
scriviamo con la seconda legge di Kirchhoff.
Nel disegnare le correnti scegliamo un verso arbitrario
Per scrivere le equazioni scegliamo il verso di percorrenza orario nelle maglie che utilizzeremo
ܫଵ = ܫଶ + ܫଷ
ܧଵ + ܧଶ + ܧଷ − ܴଵଶ ܫଵ − ܴହ ܫଶ = 0
ܧଵ + ܧଶ + ܧଷ − ܧସ − ܴଵଶ ܫଵ − ܴଷସ ܫଷ = 0
ܫଵ = ܫଶ + ܫଷ
ܧଵ + ܧଶ + ܧଷ = ܴଵଶ (ܫଶ + ܫଷ ) + ܴହ ܫଶ
ܧଵ + ܧଶ + ܧଷ − ܧସ = ܴଵଶ (ܫଶ + ܫଷ ) + ܴଷସ ܫଷ
ܫଵ = ܫଶ + ܫଷ
ܧଵ + ܧଶ + ܧଷ = ܴଵଶ ܫଶ + ܴଵଶ ܫଷ + ܴହ ܫଶ
ܧଵ + ܧଶ + ܧଷ − ܧସ = ܴଵଶ ܫଶ + ܴଵଶ ܫଷ + ܴଷସ ܫଷ
ܫଵ = ܫଶ + ܫଷ
ܫଵ = ܫଶ + ܫଷ
ܧଵ + ܧଶ + ܧଷ = (ܴଵଶ + ܴହ )ܫଶ + ܴଵଶ ܫଷ
4,5ܸ = 6ܭΩܫଶ + 3ܭΩܫଷ
ܧଵ + ܧଶ + ܧଷ − ܧସ = ܴଵଶ ܫଶ + (ܴଵଶ + ܴଷସ )ܫଷ
0 = 3ܭΩܫଶ + 6ܭΩܫଷ
ܫଵ = ܫଶ + ܫଷ
ܫଵ = ܫଶ + ܫଷ
4,5ܸ = 6ܭΩܫଶ + 3ܭΩܫଷ
4,5ܸ = 6ܭΩܫଶ + 3ܭΩܫଷ
3ܭΩܫଶ = −6ܭΩܫଷ
ܫଶ = −2ܫଷ
ܫଵ = ܫଶ + ܫଷ
4,5ܸ = −12ܭΩܫଷ + 3ܭΩܫଷ
ܫଵ = ܫଶ + ܫଷ
4,5ܸ
ܫଷ =
−9ܭΩ
ܫଶ = −2ܫଷ
ܫଶ = −2ܫଷ
ܫଵ = 0,5݉ܣ
ܫଷ = −0,5݉ܣ
ܫଶ = 1݉ܣ
Il segno negativo della I3 vuol dire che la corrente ha verso opposto a quello della freccia disegnata
ܲଵ = ܧଵ ܫଵ = 1,5ܸݔ0,5݉ = ܣ0,75ܹ݉
ܲଵ = ܲଶ = ܲଷ
ܲସ = ܧସ (−ܫଷ ) = 0,75ܹ݉












