II Compitino di Fisica Generale di Ingegneria CIVILE 2008.
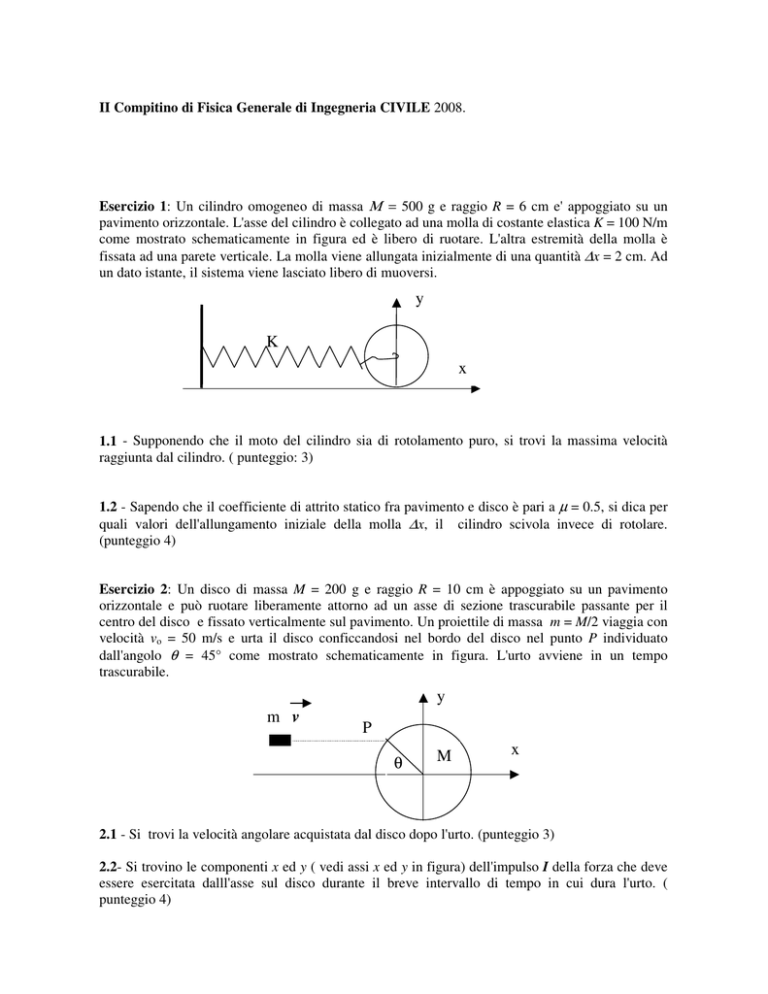
Esercizio 1: Un cilindro omogeneo di massa Μ = 500 g e raggio R = 6 cm e' appoggiato su un
pavimento orizzontale. L'asse del cilindro è collegato ad una molla di costante elastica K = 100 N/m
come mostrato schematicamente in figura ed è libero di ruotare. L'altra estremità della molla è
fissata ad una parete verticale. La molla viene allungata inizialmente di una quantità ∆x = 2 cm. Ad
un dato istante, il sistema viene lasciato libero di muoversi.
y
K
x
1.1 - Supponendo che il moto del cilindro sia di rotolamento puro, si trovi la massima velocità
raggiunta dal cilindro. ( punteggio: 3)
1.2 - Sapendo che il coefficiente di attrito statico fra pavimento e disco è pari a µ = 0.5, si dica per
quali valori dell'allungamento iniziale della molla ∆x, il cilindro scivola invece di rotolare.
(punteggio 4)
Esercizio 2: Un disco di massa M = 200 g e raggio R = 10 cm è appoggiato su un pavimento
orizzontale e può ruotare liberamente attorno ad un asse di sezione trascurabile passante per il
centro del disco e fissato verticalmente sul pavimento. Un proiettile di massa m = M/2 viaggia con
velocità vo = 50 m/s e urta il disco conficcandosi nel bordo del disco nel punto P individuato
dall'angolo θ = 45° come mostrato schematicamente in figura. L'urto avviene in un tempo
trascurabile.
y
m v
P
θ
M
x
2.1 - Si trovi la velocità angolare acquistata dal disco dopo l'urto. (punteggio 3)
2.2- Si trovino le componenti x ed y ( vedi assi x ed y in figura) dell'impulso I della forza che deve
essere esercitata dalll'asse sul disco durante il breve intervallo di tempo in cui dura l'urto. (
punteggio 4)
Esercizio 3: Un tavolo ha forma quadrata e i vertici consecutivi del piano quadrato di massa M = 50
kg sono A,B,C e D. Il tavolo possiede solamente tre gambe di massa m = 3 kg ciacuna poste nei tre
vertici consecutivi A,B,C.
D
C
A
B
3.1- Si trovi la reazione normale R del pavimento sulla gamba posta in contatto con il vertice A. (
suggerimento: si tenga conto della simmetria del problema). (punteggio 4)
Esercizio 4:Un palloncino sferico di massa m =25 g viene riempito con Elio in presenza
dell'atmosfera a temperatura ambiente T =25° C e a pressione p = 2 Atm fino a raggiungere un
raggio R = 20 cm. Il palloncino è collegato con una lunga cordicella. Si osserva che il palloncino si
solleva da terra fino ad arrivare ad un'altezza h =10 m. Quale è la massa per unità di lunghezza λ
della cordicella nell'ipotesi che l'Elio si comporti come un gas perfetto?
( per la densità dell'aria si assuma ρA= 1.29 kg/m3 mentre per la massa molecolare dell'Elio di
assuma ME = 4 g). ( punteggio 4)
Esercizio 5: La condotta principale di acqua in uno stabile si trova parallela al suolo ed è costituita
da un tubo di raggio R = 5cm. L'acqua viene portata nei vari appartamenti per mezzo di tubi di
raggio r = 1 cm. Se la pressione presente nel condotto principale è p = 5 Atm, quanta acqua ( litri al
secondo) esce da un rubineto aperto ad un altezzza h = 10 m dal suolo. Si supponga che tutti gli altri
rubinetti dello stabile siano chiusi e che l'acqua si comporti come fluido ideale. Si assuma, inoltre,
per la densità dell'acqua il valore ρ = 1000 Kg/m3 e per la pressione atmosferica il valore di 1 Atm.
( punteggio 4)
Esercizio 6: Una bacinella, di capacità termica trascurabile, contiene un litro di acqua a temperatura
Ta = 50 °C. Nell'acqua viene immerso un cubetto di marmo di capacità termica Cm =200 cal/ K a
temperatura Tm = -12 °C e un blocchetto di rame a temperatura Tr = 72 °C e di capacità termica Cr =
50 cal/ K. Tutto il sistema è isolato termicamente. Si calcoli la temperatura finale raggiunta
dall'acqua. (punteggio 3)
(si assuma ρ = 1000 Kg/m3 per la densità dell'acqua, c = 1000 cal/ Kg K per il calore specifico
dell'acqua)
Esercizio 7: Un gas perfetto biatomico con n = 2 moli compie un ciclo reversibile. Inizialmente il
gas si trova a volume Vi = 1 litro e alla temperatura Ti =100 °C ( stato A). Quindi, il gas viene fatto
espandere in modo isotermo fino a raggiungere il volume finale Vf = 3 Vi ( stato B). Quindi, il gas
viene portato ad una temperatura Tf = 25 °C mantenendo costante il suo volume ( stato C).
Dopodichè, il gas viene compresso a temperatura costante fino a tornare al volume iniziale Vi ( stato
D). Infine, la temperatura viene riportata al valore iniziale Ti mantenendo il volume costante.
Si determini il calore complessivo assorbito dal gas durante l'intero ciclo. (punteggio 4)
(Nei vari esercizi si assuma per la costante dei Gas il valore R = 8.31 J mol-1 K-1 e la conversione
1 Atm = 1.01 105 Pa. )
Soluzione Es.11.1 - Poichè il moto è di rotolamento puro, l'energia meccanica si conserva. L'energia cinetica e,
quindi, la velocità è massima nel punto in cui l'energia potenziale della molla è nulla ( punto di
riposo della molla). L'energia iniziale è tutta potenziale ed è pari a:
1
Ei = K∆x 2
(1)
2
mentre quella finale è
1
1 MR 2 2 3
ω = Mv 2
E f = Mv 2 +
(2)
2
2 2
4
dove abbiamo utilizzato la condizione di rotolamento v = ω R. Imponendo l'uguaglianza delle
energie si trova:
2 K
v=
∆x = 0.231 m/s
(3)
3M
1.2 - Il cilindro scivola se il modulo della forza di attrito statico F necessaria per farlo rotolare è
superiore alla massima forza di attrito statico µMg. Per calcolare il valore di F necessario per il
rotolamento, bisogna scrivere le equazioni Cardinali della Dinamica per le forze e per i momenti di
forza. Scriviamo le equazioni utilizzando come Polo il centro di massa. La I equazione (equazione
delle forze lungo l'asse x in figura) è:
− K∆x + F = Ma
(4)
dove F ed a sono le componenti x della forza e dell'accelerazione. La II equazione Cardinale per il
momento lungo l'asse passante per il C.M. è
R2
R
a
FR = M
α = −M a
F = −M
(5)
2
2
2
dove i segni - derivano dall'esecuzione del prodotto vettoriale a = α x R dove R indica il vettore
che collega il punto di contatto del cilindro sul pavimento con il C.M. Sostituendo la (5) nella (4) si
trova, dopo semplici passaggi algebrici:
K∆x
F=
(6)
3
Il cilindro scivola se |F| > µMg , cioè se:
3µMg
∆x >
= 7.35 cm
(7)
K
⇒
Soluzione Es. 2
2.1 - Nell'urto, l'unica forza impulsiva che agisce sul sistema dei due corpi è la forza esercitata
dall'asse. Poichè tale forza ha momento nullo rispetto all'asse, durante l'urto si conserva il momento
della q.m. del sistema. Dunque:
M 2
mvo R sin(45°) = mR 2 +
R ω = 2mR 2ω
2
da cui si deduce:
v
ω = o = 177 rad/s
2 2R
(1)
(2)
2.2 - L'unica forza impulsiva agente sul sistema dei due corpi è quella esercitata dall'asse. Dunque,
l'Impulso di tale forza è anche uguale alla variazione di quantità di moto (q.m.) del sistema.
Inizialmente, la q.m. del disco è nulla e, quindi, la q.m. totale è dovuta solamente alla q.m. del
proiettile. Dunque, la q.m. iniziale è
pi = ( mvo, 0)
(3)
Dopo l'urto, il centro di massa del disco è ancora fermo, dunque anche la sua q.m. è ancora nulla e
la q.m. totale è solo quella del proiettile che, ora, si trova sulla superficie del disco nel punto
individuato dall'angolo θ e ruota con la velocità angolare del disco. Dunque:
mωR mωR mvo mvo
pf =
,
,
(4)
=
4
2 4
2
L'impulso della forza è I = pf -pi , cioè:
− 3mvo mvo
,
I =
(5)
= ( -3.75 Ns, 1.25 Ns)
4
4
Soluzione Es. 3 La risposta al quesito si trova imponendo l'equilibrio delle forze e dei momenti. Per la simmetria
del problema, le reazioni normali sulle gambe in A e C sono uguali e, perciò, le indichiamo con lo
stesso simbolo R, mentre la reazione sulla gamba B si indicherà con RB. L'equilibrio delle forze si
scrive:
RB + 2 R = (M + 3m )g
(1)
Un'altra equazione si ottiene imponendo che una componente del momento di forza totale sia
uguale a zero. Prendiamo come polo il punto di contatto fra la gamba posta in B e il pavimento e
consideriamo la componente del momento di forza lungo l'asse parallelo a BC. Le uniche forze che
danno un contributo a tale momento sono: la forza peso del piano applicata al centro del piano, la
forza peso della gamba in A e la reazione vincolare R della gamba in A. L'equilibrio delle
componenti dei momenti lungo BC si scrive, perciò:
M
MgL
(2)
+ mgL = RL
R = m + g = 274 N
2
2
sostituendo nella (1) si deduce RB = mg.
⇒
Soluzione Es.4 -
Il palloncino si ferma quando la forza di Archimede equilibria la forza peso dovuta alla massa del
palloncino, a quella dell'elio e a quella della corda di lunghezza h. Dunque:
4π 3
4π 3
ρAg
R = ρE g
R + mg + λgh
(1)
3
3
da cui si deduce:
(ρ A − ρ E ) 4π R 3 − m
3
(2)
λ=
h
Resta da calcolare la densità dell'Elio ρE. Dalla legge dei gas perfetti:
M
pV =
RT
(3)
ME
dove M = massa dell'Elio. Dunque, la densità dell'Elio è
pM E
M
ρE =
=
= 0.324 Kg/m3
(4)
V
RT
Sostituendo la (4) nella (2) si trova
λ = 7.3 10 - 4 kg/m = 0.73 g/m
(5)
Soluzione Esercizio 5 - La pressione all'uscita del rubinetto è quella atmosferica po. Dunque, per il
Teorema di Bernulli:
1
1
p + ρv 2 = ρvo2 + p o + ρgh
(1)
2
2
dove v è la velocità nel tubo principale e vo quella nella cannella.Per la conservazione della massa:
R2
vo = v 2 = 25v
(2)
r
Dunque, dopo semplici passaggi algebrici, si trova:
2( p − p o − ρgh)
= 1.4 m/s
v=
(3)
R4
4 − 1 ρ
r
Dunque, la portata nella condotta, che è uguale a quella in uscita dal rubinetto è:
(4)
q = πR 2 v = 110 10 - 4 m3/s = 11 litri/s
Soluzione Es.6 - Indicando con Tf la temperatura finale, si deve imporre che la somma dei calori
assorbiti da tutti i corpi per raggiungere la temperatura finale sia uguale a zero ( il sistema è isolato
termicamente). I calori assorbiti dall'acqua ,dal rame e dal marmo sono dati da
Qa = c Ma (Tf -Ta)
(1)
Qr = Cr (Tf -Tr)
(2)
Qm = Cm (Tf -Tm)
(3)
Imponendo che la somma sia nulla si ricava facilmente:
cM a Ta + C mTm + C r Tr
Tf =
= 41°C
cM a + C m + C r
(4)
Soluzione Es.7 - Il calore totale assobito durante l'intero ciclo è pari al lavoro fatto nel ciclo. Poichè
il lavoro fatto nei tratti isocori (BC e CA) è nullo, il lavoro è pari solamente alla somma dei lavori
fatti nei tratti isotermi (AB e CD), cioè:
V
L = nR (Ti − T f ) ln i = 1.38 103 J
(1)
Vf
dunque, QTotale = L = 1.38 103 J
(2)












