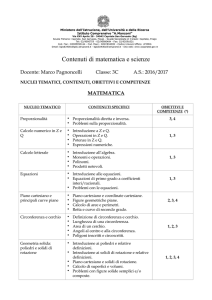
Programma di matematica
Anno scolastico 2015-2016
svolto nella classe terza D
Prof.ssa Antonella Cicalò
2.1.1. Relazioni tra grandezze
Grandezze costanti, grandezze variabili e relazioni tra grandezze
Concetto di funzione
Relazioni di proporzionalità diretta ed inversa tra grandezze: definizioni, costanti di
proporzionalità, funzioni caratteristiche, proprietà
2.1.2. Il numero
Le esigenze matematiche che inducono ad ampliare gli insiemi numerici
L’insieme R dei numeri reali relativi e la loro rappresentazione sulla retta numerica
Significato ed importanza del segno nel conferire valore ad un numero: valore assoluto e valore
relativo di un numero
Ordinamento e confronto tra numeri relativi
Operazioni con i numeri relativi: l’addizione, la sottrazione, l’addizione algebrica, la
moltiplicazione, la divisione, l’elevamento a potenza e l’estrazione di radice quadrata
2.1.3. Calcolo letterale, polinomi ed equazioni
Lettere al posto di numeri: le espressioni letterali ed il loro significato
Calcolo del valore di un’espressione letterale
I monomi: definizioni e caratteristiche
Operazioni ed espressioni con i monomi
I polinomi: definizioni e caratteristiche
Calcolo del valore di un polinomio
Addizioni e sottrazioni di polinomi
Moltiplicazione di monomi e polinomi
Prodotti notevoli ( somma per differenza di un binomio e quadrato e di un binomio)
Le equazioni come strumento matematico per risolvere problemi
La relazione di uguaglianza: identità ed equazioni
Definizione di equazione e tipi di equazioni (ad una o due incognite, di primo o di secondo
grado)
Principi di equivalenza
Risoluzione di equazioni di primo grado
Equazioni e formule inverse
Tradurre problemi in equazioni
2.1.4. Elementi di geometria analitica: piano cartesiano, equazioni e linee
Il piano cartesiano e le coordinate dei punti su tale piano: definizioni e caratteristiche
Posizioni reciproche di punti e rette sul piano cartesiano
Misura di distanze tra punti (lunghezze di segmenti) sul piano cartesiano a partire dalle
coordinate dei punti
Rappresentazione di poligoni sul piano cartesiano e calcolo dei loro perimetri ed aree a partire
dalle coordinate dei vertici
L’equazione di una retta passante per l’origine di un sistema di riferimento cartesiano
Il coefficiente angolare di una retta
Equazioni di rette non passanti per l’origine: il termine noto
Relazioni tra i coefficienti angolari di rette parallele e tra quelli di rette perpendicolari
Risoluzione grafica di un’equazione di primo grado mediante l’equazione di una retta
Punto di intersezione tra due rette e sue coordinate
Rappresentazioni di relazioni tra grandezze mediante rette passanti per l’origine ed iperboli (richiamo
alle nozioni ed ai concetti relativi alla proporzionalità diretta ed inversa): il significato
Geometria
2.2.1 Misure di circonferenza e cerchio
Il rapporto tra circonferenza e diametro di un cerchio: il numero
Calcolo della lunghezza della circonferenza e le formule inverse
Relazione di proporzionalità diretta tra la lunghezza dell’arco di circonferenza ed il
corrispondente angolo al centro: calcolo di lunghezze di archi e di ampiezze di angoli al centro
Misurazione dell’area di un cerchio e rapporto tra area del cerchio e quadrato del raggio
Calcolo dell’area del cerchio come caso limite delle aree di poligoni regolari inscritti e circoscritti
alla circonferenza: formula diretta ed inversa
Calcolo dell’area della corona circolare
Relazione di proporzionalità diretta tra l’area di un settore circolare ed il corrispondente angolo al
centro: calcolo dell’area di un settore circolare
Relazione di proporzionalità diretta tra le aree dei settori circolari e le lunghezze degli archi
corrispondenti
2.2.2. Le figure nello spazio: nozioni e concetti generali
Gli enti geometrici nello spazio: punti, rette e piani e loro relazioni; il diedro
Classificazione delle figure solide
Caratteristiche generali dei poliedri :relazione di Eulero
Caratteristiche generali dei solidi a superficie curva, in particolare dei solidi dei rotazione
La misura degli elementi dei solidi geometrici: le lunghezze degli spigoli, lo sviluppo dei solidi
su un piano e le loro superfici, il volume e la sue unità di misura
La relazione di equivalenza tra solidi: confronto di volumi
Il peso specifico
Il principio di Cavalieri: dalla misura al calcolo del volume dei solidi
2.2.3. I poliedri: prismi, piramidi, poliedri regolari
Il parallelepipedo rettangolo come solido di riferimento per il calcolo dei volumi
Il parallelepipedo: definizione, caratteristiche e sviluppo in piano, calcolo della diagonale,
dell’area laterale e totale e del volume
Il cubo: definizione, caratteristiche e sviluppo in piano, calcolo della diagonale, dell’area laterale
e totale e del volume
I prismi: definizione e caratteristiche; sviluppo in piano di un prisma retto a base triangolare,
calcolo dell’area laterale e totale di un prisma retto e calcolo del suo volume
La classificazione dei prismi
Le piramidi: definizione, caratteristiche ed elementi (altezza ed apotema)
Sviluppo su un piano della superficie laterale di una piramide e calcolo dell’area laterale e di
quella totale
Calcolo del volume di una piramide
Definizione, descrizione e proprietà dei poliedri regolari
Calcolo dell’area di un poliedro regolare
Classificazione generale dei poliedri
2.2.4. I solidi di rotazione
Il cilindro: definizione e costruzione, elementi, sviluppo, area laterale e totale, volume; casi
particolari: il cilindro equilatero
Il cono: definizione e costruzione, elementi, sviluppo, area laterale e totale, volume; casi
particolari: il cono equilatero
3. Elementi di Statistica e Probabilità
2.3.1 Cenni di statistica
Raccolta, presentazione, lettura ed elaborazione di dati statistici
2.3.1 Cenni di probabilità
Definizione classica di probabilità
Frequenza assoluta e frequenza relativa di un evento
Definizione frequentista di probabilità
- Probabilita' semplice
probabilita' composta: eventi indipendenti e eventi dipendenti
probabilita' totale: eventi disgiunti e eventi disgiunti