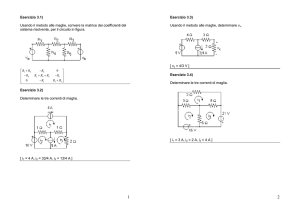
Collegamento resistori
Resistore = conduttore che presenta tra due estremi una resistenza R,
è fornito di due reofori di resistenza trascurabile rispetto a R
= elemento circuitale passivo, lineare e bilaterale
Circuiti equivalenti
Circuito composto di più resistori → tra due suoi terminali è possibile
determinare una resistenza equivalente R T per la quale si può scrivere
RT = ε / I dove ε è la ddp applicata ai terminali da un generatore e I la
corrente da esso fornita.
Circuiti
equivalenti
Resistori in serie
Resistori in parallelo
Applicazioni
Applicazioni
Applicazioni
trasformazioni
triangolo
stella
trasformazioni
stella
triangolo
trasformazioni
triangolo
stella
Leggi di Kirchhoff
Definizioni
Circuito: insieme di conduttori che si chiude su se stesso, comprendente uno o
più generatori di fem
Rete:
insieme di circuiti collegati tra loro (lineare se conduttori ohmici e fem
costanti)
Nodo:
punto della rete in cui si incontrano tre o più conduttori
Ramo: conduttore fra due nodi
Maglia: successione chiusa di rami (ognuno percorso una sola volta)
La prima legge di Kirchhoff o dei nodi
La somma algebrica delle correnti che si incontrano in un nodo è nulla
(discende dalla condizione di stazionarietà → div = 0 → flusso di su superficie
chiusa contenente il nodo = 0)
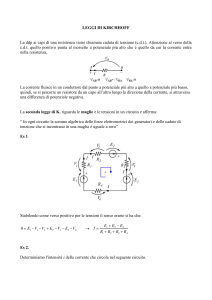
La seconda legge di Kirchhoff o delle maglie
In una maglia la somma algebrica delle cadute ohmiche è uguale alla somma
algebrica delle fem eventualmente presenti nella maglia stessa
(discende dal fatto che il campo e all'esterno dei conduttori è conservativo e quindi vale
la relazione
)
Applicazioni
Risoluzione di un circuito
Determinazione delle correnti, in valore e segno, nei vari rami del circuito
Regime stazionario → Leggi di Kirchhoff
– I legge → Σ i k = 0 ad ogni nodo
– II legge → per ogni maglia :
a) scelta senso positivo di percorrenza
b) cadute ohmiche positive quelle prodotte da
correnti concordi con senso positivo
c) fem positive quelle attraversate da – a + dal senso
d) Σ i k R k = Σ Ɛj
– Risultato: n equazioni > m correnti incognite (equazioni non indip.)
– Metodo delle correnti di maglia: permette di ottenere m equazioni
indipendenti
Metodo delle correnti di maglia
a) scelta dello senso positivo di percorrenza per tutte le maglie
b) selezione delle maglie “reali” ovvero delle maglie costituite da un insieme
chiuso di rami individuabili all'interno della rete senza la soppressione di alcun
ramo
c) definizione delle “correnti di maglia”, una per ogni maglia reale
(le correnti di ramo coincideranno con quelle di maglia se il ramo farà parte di una
sola maglia oppure saranno date dalla somma algebrica delle correnti di maglia delle
due maglie che lo hanno a comune)
Metodo delle correnti di maglia
⎧R1J1 + R2( J1- J2 ) = Ɛ1
⎟
⎨R2(J2-J1)+R3J2+R 4(J2-J 3) = - Ɛ3
⎟
⎩R4(J3-J2) + R5J3 + R6J3 = Ɛ3 - Ɛ2
Se ci fosse solo Ɛk avremmo Jk = ƐkDet Mkk /Det(akl ) = Ɛk / RTk
e quindi i termini Det Mkk /Det(akl ) rappresentano l'inverso della resistenza
equivalente a tutto il circuito vista da Ɛk tra i suoi terminali quando gli altri
generatori siano tutti cortocircuitati.
Principio di sovrapposizione
In base a quanto visto nella applicazione del metodo delle maglie avremo
in generale
con Ɛi somma algebrica delle fem presenti nella maglia i-esima e eS fem
dei generatori presenti nella rete. Da questa segue il
Principio di Sovrapposizione: “La corrente totale attraverso ogni elemento
di una rete lineare avente generatori indipendenti, è uguale alla somma
algebrica delle correnti prodotte nell'elemento da ciascun generatore
agente separatamente”
Applicazione
(stesso risultato ottenibile con il metodo delle maglie)