PRIMA SIMULAZIONE di TERZA PROVA: FISICA
Soluzioni
Domanda n. 1
Enuncia le leggi di Kirchhoff, specificando cosa sono i nodi e le maglie di un circuito.
Legge dei nodi: la somma delle intensità delle correnti entranti in un nodo è uguale alla somma di
quelle uscenti oppure equivalentemente la somma algebrica delle intensità di correnti in un nodo è
nulla. Tale legge deriva dal principio di conservazione della carica. Un nodo è il punto di un
circuito in cui arrivano 3 o più rami.
Legge delle maglie: in una maglia la somma algebrica delle forze elettromotrici è uguale alla
somma algebrica delle cadute di tensione ai capi degli utilizzatori. Una maglia è un qualunque
circuito chiuso.
Precisazione non richiesta: il segno delle fem dipende da come il generatore è inserito rispetto al verso di percorrenza
della maglia, mentre il segno delle cadute di tensione dipende dal verso della corrente rispetto a quello di percorrenza
della maglia. In pratica si hanno le seguenti possibilità:
+fem
-fem
Verso della corrente
Verso della corrente
+RI
verso della maglia
verso della maglia
-RI
verso della maglia
verso della maglia
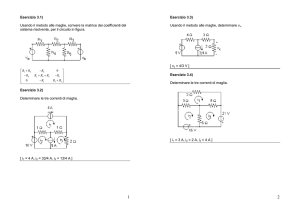
Utilizzate il metodo delle correnti di ramo, scrivi il sistema risolvente del seguente circuito:
Osserviamo che BB’ non è un ramo, poiché non è inserito alcun
elemento, quindi B e B’ sono un unico nodo. Fissata una
corrente per ogni ramo le legge dei nodi diventa:
A : I1 + I 2 = I 3
B : I 4 + I 5 = I 2 + I 1 (osserviamo che l’equazione del nodo B è
fem1
A
fem2
I3
I1
R1
I2 maglia 2
R2
B
C : I3 = I4 + I5
la somma delle altre due, quindi ci sono 2 equazioni
indipendenti)
Fissato un verso di percorrenza per tre maglie indipendenti, le
legge delle maglie diventa:
1 : fem1 = R1 I 1 − R2 I 2
maglia 1
B’
R3
C
maglia 3
R4
I4
fem3
I5
2 : fem2 = R2 I 2 + R3 I 4 Il sistema costituito dalle 3 equazioni delle maglie e 2 dei nodi ha 5
3 : fem3 = R4 I 5 − R3 I 4
incognite in 5 equazioni indipendenti e quindi è il sistema risolvente.
Domanda n. 2
Spiega cos’è l’energia elettrostatica di un sistema di cariche e scrivine l’espressione per un
condensatore con carica Q, posto ad una differenza di potenziale ∆V. Ricava l’espressione
dell’energia elettrostatica in funzione del campo elettrico.
L’energia elettrostatica rappresenta il lavoro che è necessario spendere per creare una data
distribuzione di cariche e di conseguenza un dato campo elettrico nello spazio.
Simulazione di terza prova 5D
1
Nel caso di un condensatore è quindi il lavoro che è necessario compiere per caricarlo, in funzione
1
di carica e differenza di potenziale è dato da: W = Q∆V , ricordando la definizione di capacità si
2
Q2
1
.
hanno le seguenti espressioni equivalenti: W = C∆V 2 , W =
2
2C
Ricordando che in un condensatore piano con armature di area S, poste a distanza d valgono le
σ
Q
seguenti relazioni: E =
=
quindi Q = ESε 0 e ∆V = Ed si ottiene sostituendo l’espressione
ε 0 Sε 0
1
1
dell’energia immagazzinata in funzione del campo: W = Q∆V = ε 0 E 2 Sd
2
2
Commenta le seguenti affermazione specificando se sono vere o false.
a) Raddoppiando la carica presente sulle armature del condensatore raddoppia l’energia
immagazzinata.
Q2
(falso) considerando l’espressione W =
e ricordando che la capacità di un condensatore non
2C
dipende dalla carica presente si osserva che l’energia è direttamente proporzionale al quadrato della
carica, quindi raddoppiando la carica l’energia quadruplica.
b) Il grafico dell’energia immagazzinata in un condensatore in funzione della differenza di potenziale
applicata è una retta passante per l’origine
1
W
(falso) considerando l’espressione W = C∆V 2 e ricordando che la capacità di
2
un condensatore non dipende dalla differenza di potenziale tra le armature si
osserva che l’energia è direttamente proporzionale al quadrato della differenza di
potenziale, quindi il grafico di W in funzione di ∆V è una ramo di parabola
Simulazione di terza prova 5D
2
∆V