Grafici
1) Rappresentare il grafico della funzione di equazione y = - 3 + 9x+2 , determinare l’equazione
dell’asintoto e le intersezioni con gli assi cartesiani
A partire dal grafico ottenuto rappresentare y = | - 3 + 9x+2 |
x +1
2) Rappresenta i grafici delle funzioni: f ( x) = 3 x +1 − 4 , g ( x) = 3 − 4 . A partire dai grafici
ottenuti rappresenta le funzioni y = f (x) e y = g (x) . Ricava le coordinate dei punti
d’intersezione di ciascuna funzione con gli assi cartesiani.
1
+ log 1 ( x + 8) , determinare
4
2
l’equazione dell’asintoto e le intersezioni con gli assi cartesiani
3) Rappresentare il grafico della funzione di equazione y = −
4) Rappresentare il grafico della funzione di equazione y = log 2
4
x
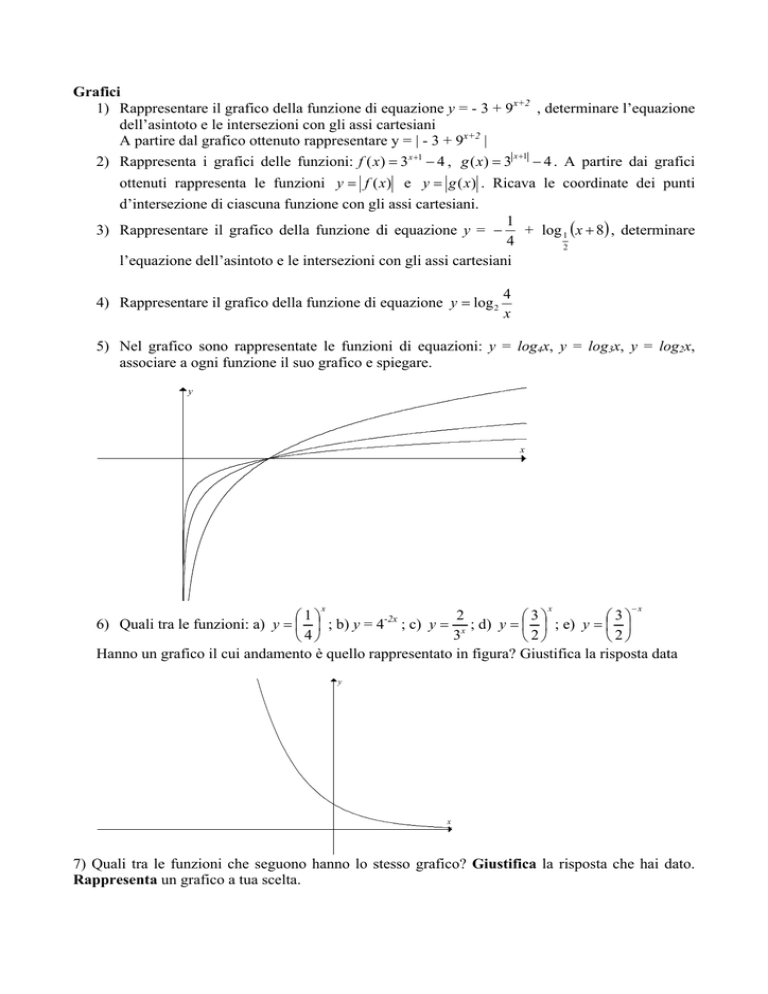
5) Nel grafico sono rappresentate le funzioni di equazioni: y = log4x, y = log3x, y = log2x,
associare a ogni funzione il suo grafico e spiegare.
y
x
x
x
−x
2
⎛3⎞
⎛1⎞
⎛3⎞
6) Quali tra le funzioni: a) y = ⎜ ⎟ ; b) y = 4-2x ; c) y = x ; d) y = ⎜ ⎟ ; e) y = ⎜ ⎟
3
⎝2⎠
⎝4⎠
⎝2⎠
Hanno un grafico il cui andamento è quello rappresentato in figura? Giustifica la risposta data
y
x
7) Quali tra le funzioni che seguono hanno lo stesso grafico? Giustifica la risposta che hai dato.
Rappresenta un grafico a tua scelta.
a.
y=
2
4x
b. y =
2x
2
c. y = 4
1− 2 x
2
d. y = 2
x−2
2
e. y = 21− 2 x .
⎛ x⎞
8) Rappresenta in uno stesso sistema di riferimento le funzioni di equazione y = log 2 ⎜1 − ⎟ e
⎝ 2⎠
y = log 1 (3 x + 1) . Verifica che A(1; - 1) è un punto d’intersezione dei due grafici.
4
x⎞
⎡ 1
⎤
⎛
Risolvi graficamente la disequazione log 2 ⎜1 − ⎟ ≤ log 1 (3x + 1) . ⎢− < x ≤ 0 ∪ 1 ≤ x < 2⎥
⎝ 2⎠
⎣ 3
⎦
4
9) E’ assegnata la funzione di equazione y = −1 + log 2 ( x + 4)
a) rappresenta la funzione assegnata
b) verifica che la funzione assegnata e la retta r di equazione x – 3y + 2 = 0 hanno in comune i
x+2
.
punti di ordinata 0 e di ordinata 2. Risolvi la disequazione − 1 + log 2 ( x + 4) <
3
c) Rappresenta la funzione di equazione y = − 1 + log 2 ( x + 4)
1⎞
⎛
10) Rappresenta la funzione che ha equazione y = log 3 ⎜ x + ⎟
3⎠
⎝
1⎞
⎛
Come otterresti dal grafico ottenuto il grafico di y = log 3 9⎜ x + ⎟ ? Perché? Rappresentalo.
3⎠
⎝
Disequazioni esponenziali
x
>1
2) 2
1
x+2
5) 3 + 3 x > 10
1) 6 x
2
−1
2
7) 53 x + 6 x > log 4
x
10) 2 + e 2 +
−
4
x
3
7
6) 4·2x + x
≤0
2 −4
1
64
3
[∀x]
x+2
−4≥ 0
6 ⋅ 2x
> −1
4x − 7
8)
4) 3x >
2
3 −1
x
9) 4 x − 2 < 2 x
[ x < 1 ∪ x > 4]
>0
x
2
1
3) 3 x +3 +
≥ 41− x
e −2
Disequazioni logaritmiche
1) log 1 x 2 + 2 x ≥ −1
(
)
3
2) log 4 x + log 4 ( x − 1) ≤
1
+ log 4 (5 − x 2 )
2
2
4) log 2 ( x + 1) + 3 log 8 ( x + 1) ≤ 2
(
)
6) log 4 x 3 − 2 x ≤ log 2 x
3) log 1 ( x 2 − 1) − log 4 ( x 2 − 1) > 9
2
5) log 4 ( x + 5) − log 4 ( x 2 + 2) < −
7) log 2 log 1
2
(
)
2
)
9) log 1 log 2 4 x − 1 > 0
3
3
10) log 4
1
− log16 x 2 > 5
x
12) log 3 ( x + 1) > 2
2
2
1
⎤
⎡
⎢⎣0 < x ≤ 4 ∪ 1 < x ≤ 4⎥⎦
11) log 1 x + log x 16 ≥ 0
2
13)
14) log10 x 2 + log100 x 2 −
3
>0
2
4 + log 2 x ≥ 2 + log 2 x
[ x < - √10 ∪ x > √10 ∪ −
1
1
<x<
]
10 10
10 10
Equazioni
1) 8 = 4 ⋅ 2
x
4) 126⋅ 5
[ - 5 < x < - 2 ∪ x > 4]
1
> 1 [x < - √3 ∪ x > √3 ]
x +1
(
8) log 1 log 4 x 2 − 1 > 0
1
2
−
2− x
2
x2
2)
− 5 ⋅ 52
1
3
+ x
=2
2 −1 2 +1
2x
2− x
= 25
[ x = - 2]
6) 3x+2 + 2 x+2 = 3x−1 + 2 x [nessuna soluzione]
7) log 2 (x 2 + 5 x ) − 2 log 4 ( x + 2) = 1
8) ln(4x +1) + ln(4x - 7) – ln9 = 0 [x = 2]
3) 4 5) 2 x +1 +
17
1
3
+ 2 x−2 = x−2
x
4
4
4
3
=3
1+ 2x
9) Log 2 ( x 2 + x) + Log ( x) + Log ( x + 1) = 0
10)
11
2
2 + Logx
+
=
2
Log x − 4 Logx + 2 Logx − 2
5
5
Funzioni
Sono assegnate due funzioni f, g scrivere le equazioni di f ° g, g
ciascuna delle due funzioni composte
1) f(x) = lnx
1
g(x) =
1 − x2
3) f ( x) = x
g ( x) =
•
1) y =
1⎤
⎡
⎢⎣ x = − 25 ⎥⎦
11) log 1 x 2 − log 1 (− x 3 ) = −2
f e calcolare il dominio di
−4+ x
2) f(x) =
1
ln x − 1
°
4) f ( x) = log 1 x
⎛1⎞
g(x) = ⎜ ⎟
⎝4⎠
x
g ( x) = x 2 − 1
4
Dominio delle funzioni
1
x
5 − 10
2) y =
4) y = 3x−1 + 3x − 30
1
x
5 − 10
5) y = 31− x + 3x − 2
7) y = log 4 x 2 − 1
x
⎛1⎞
3) y = ⎜ ⎟ − 10
⎝5⎠
6) y = 4 x −
3
4x
8) y = log 2 4 x − 1
9) a. Determina il dominio della funzione di equazione y = Log log 0.2 (1 − x)
b. Determina, al variare di n (numero naturale maggiore di 1), il dominio della funzione di
equazione y = n Log log 0.2 (1 − x) .
[ n pari 0.8 ≤ x < 1; n dispari 0 < x < 1 ]
10) y =
ln ( x + 3e ) − 1
Esercizi vari
1) Rispondi negli spazi indicati sul testo
1
• log 5 a =
vera se a .... perché
log 1 a
5
....................................................................................................................................................
falsa per ogni a perché
....................................................................................................................................................
•
log 5 a =
1
vera se a ... perché
log a 5
....................................................................................................................................................
falsa per ogni a perché
....................................................................................................................................................
•
Log(a) + Log(- a) = 0 vera se a ... perché
....................................................................................................................................................
falsa per ogni a perché
....................................................................................................................................................
⎛ 3⎞
Risolvi con il metodo che ritieni più opportuno la disequazione e < ⎜ ⎟
⎝5⎠
2x
x
2) Se a, b sono due numeri positivi, e k è un numero positivo diverso da 1, per quali valori di k si
ha: log k (a 2 + b 2 ) > 2 log k (a + b) ?
3) La disuguaglianza Log
vera solo per a > 0
1
2
< log 1 2
a +1
2 a +3
2
vera per ogni a
è
falsa per ogni a
vera solo per a ≠ 0
Quale risposta è esatta? Perché?
2
Risolvi la disequazione 7 x + 4− x > log 1 25
5
4) Decidi se la seguente affermazione è vera o falsa e motiva la risposta che hai dato: “ 4 − x
2
−1
è
minore di 1 per ogni x”
5) E’ assegnata la funzione che ha equazione y = e −1+ 2− x . Per ciascuna delle affermazioni che
seguono decidi se è vera o falsa e motiva la risposta
a) la funzione è definita su tutto l’asse reale come tutte le funzioni esponenziali
b) la funzione assume valore 1 per x = 1
c) la funzione assume valori negativi se x > 2
1
d) la funzione assume valori maggiori di se x < 2
e
6) Se a è numero positivo e diverso da 1, che relazione c’è tra i grafici delle funzioni
1
1
y = log a
y = log 1 x
y = log 1 ?
y = log a x
x
a
a x










