Federico Genzo
n.matr: 68000089
15/06/04
RELAZIONE LABORATORIO INFORMATICO
Il fenomeno dei battimenti
Scopo:
Lo scopo di questa esperienza è quello di capire tramite ascolto dei suoni prodotti a quale frequenza
non c’è più il fenomeno dei battimenti, ovvero quando raggiungiamo la zona normale in cui si
distingue a orecchio che il suono ha una frequenza diversa da quella base.
Zona normale Zona confusa Regione dei battimenti Zona confusa Zona normale
Quella sottolineata in giallo è la banda critica (BC) ed la zona che ci interessa per trovare la curva
critica dei battimenti.
Teoria sul fenomeno dei battimenti:
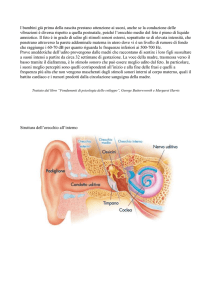
Il fenomeno dei battimenti è un fenomeno psicoacustico. Esso deriva dal fatto che se due suoni con
frequenze f0 ed f1 “vicine”, ovvero molto simili fra loro, vengono suonati assieme, il nostro sistema
uditivo percepisce un solo suono di frequenza pari alla semisomma ( f1 + f0 )/2, modulato in
ampiezza ad una frequenza pari alla semidifferenza ( f1 – f0 )/2.
Esempio:
Prendiamo due funzioni d’onda con frequenze “vicine”, le chiamiamo y1 ed y2
Y1( t ) = A * sin( 2πf0t )
Y2( t ) = A * sin( 2πf1t )
Ora, se si sommano queste due funzioni ( in altre parole come sovrapporre i due suoni ):
Ys( t ) = Y1( t ) + Y2( t )
=
=
A * sin( 2πf0t ) + A * sin( 2πf1t )
2 * A * cos( 2πΔft ) * sin( 2πfit )
E da qui ricaviamo la frequenza del suono da noi percepito ( fi ) e la sua modulazione in ampiezza
( Δf ).
fi =
f1 f 0
2
Δf =
f1 f 0
2
Ecco un grafico d’esempio che mostra la forma d’onda di un battimento:
2
1
0.05
0.1
0.15
0.2
0.25
0.3
-1
-2
L’esperienza di laboratorio:
Nell’esperienza di laboratorio informatico sui battimenti abbiamo creato uno script in cui da una
frequenza di partenza togliamo e aggiungiamo per 10 o più volte una quantità di 10 Hz.
In questo modo si riescono a produrre suoni diversi ma con frequenza vicina.
Ecco un esempio di script con frequenza base pari a 440 Hz:
#! /usr/local/bin/octave -qf
amp=1
f0=440;
durata=5;
rate=8000;
y=sinetone(f0,rate,durata,amp);
for a=1:10
f0=f0+10;
y1=sinetone(f0,rate,durata,amp);
z=[y,y1];
s=sprintf("file%d.wav",a);
ausave(s,z);
endfor
f1=f0;
for a=1:10
f1=f1-10;
y1=sinetone(f1,rate,durata,amp);
z=[y,y1];
s=sprintf("filen%d.wav",a);
ausave(s,z);
endfor
Come si può ben osservare sono stati usati due cicli “for” sia per aggiungere che per togliere 10 hz
alla frequenza base ( f0 ) per una decina o più volte, ad esempio 440 Hz si aggira tra 340 Hz ( limite
inferiore ) e 540 Hz ( limite superiore ).
Il lavoro sopra descritto è stato ripetuto con 4 frequenze base diverse rispettivamente di:
440,1000,1200,1500 Hz.
Tabella dati:
f
440
1000
1200
1500
f (inferiore)
400
910
1080
1370
f (superiore)
480
1090
1300
1610
BC
80
180
220
240
n. prove
20
20
30
30
f ( inferiore ) e f ( superiore ) rappresentano le frequenze dei suoni che per primi entrano a far parte
della zona normale, BC è la larghezza della banda critica ( la differenza fra le due frequenze appena
citate ). N. prove sono il numero di suoni che sono stati prodotti, ognuno con una frequenza sempre
più bassa o sempre più alta rispetto a quella base ( 20 prove, ovvero 10 suoni con incremento di 10
Hz ciascuno e 10 suoni con decremento di 10 Hz ciascuno ).
Il grafico che ne risulta dalla raccolta dati ha come ascissa le frequenze base utilizzate durante le
prove e come ordinata le larghezze di banda critica ottenute:
La linea rossa nel
grafico rappresenta la
banda critica delle
prove svolte. Essa può
essere confrontata con
quella teorica, ma
ovviamente sarà molto
difficile che le due
siano identiche.
Il grafico qui a fianco mostra la curva
di banda critica teorica.
Conclusioni:
Come più volte introdotto la curva di banda critica che si voleva ottenere non poteva, salvo
miracoli, essere perfettamente identica alla curva teorica rappresentata nel grafico sopra, questo è
dovuto principalmente al nostro sistema uditivo che in ogni persona reagisce in maniera diversa e
quindi anche l’ascolto e la valutazione del suono viene fatta in maniera diversa.
Comunque sia il grafico sperimentale sarebbe stato molto più preciso se si fossero elaborate molte
più frequenze base, alla fine sono state elaborate solo 4 perché il lavoro di elaborazione descritto
richiedeva molto tempo e soprattutto molta concentrazione d’ascolto, ma nonostante questo è
risultato chiaro e apprezzabile questo tipo di fenomeno.
Il grafico che mostra la curva teorica è stato fatto adottando una scala diversa, adesso ad occhio non
è facile stabilire un confronto fra le due curve, ma sono sicuro che la curva trovata per quanto ci si
possa avvicinare non sarà mai perfettamente identica a quella teorica e neanche ad altre curve
derivanti da altre esperienze di questo tipo. Come già detto più volte il nostro orecchio è soggettivo
e ognuno interpreta i suoni simili in maniera diversa.