Geodetiche

geo home | Simboli e convenzioni | Indice compatto | Indice esteso | Indice alfabetico | home page di www.batmath.it
Capitolo N
Geodetiche
Una delle proprietà essenziali della retta, nella geometria di Euclide, è che essa realizza il cammino
di minima distanza tra due suoi punti qualsiasi. Questo concetto di minima distanza ha
un'importanza cruciale in molte applicazioni e per questo vogliamo qui affrontarlo in maniera più
approfondita, anche se schematicamente e senza alcuna pretesa di completezza, raccogliendo anche
quanto abbiamo trattato altrove.
Data una superficie S, si dice geodetica una linea γ tracciata sulla superficie che gode
della seguente proprietà: ogni arco non troppo lungo di γ, i cui estremi siano A e B, realizza il
percorso di minima distanza tra A e B, per chi si muova senza uscire dalla superficie.
Definizione.
E' molto importante segnalare che, nel piano, la precisazione che l'arco sia non troppo lungo è
ininfluente, mentre ciò non accade su altre superfici. Per esempio, come vedremo, su una sfera una
geodetica è un cerchio massimo, ma se prendiamo su un cerchio massimo due punti A e B essi
dividono il cerchio stesso in due parti, una più lunga e una più corta se i punti non sono
diametralmente opposti: uno dei due archi realizza la minima distanza, l'altro no.
La cosa ragguardevole è che se consideriamo un essere bidimensionale, costretto a vivere sulla
superficie (come gli abitanti di Flatlandia), essi trattano le geodetiche, che per noi in generale
saranno curve, esattamente come noi trattiamo le rette: per questi esseri le geodetiche sono linee
"diritte".
Procediamo ora con qualche esempio.
Geodetiche su una sfera
Su una sfera di raggio r si possono tracciare delle
circonferenze che, dal punto di vista di chi abita sulla sfera stessa, sono definite esattamente come le
definiremmo noi, esseri tridimensionali che possiamo osservare la sfera "immersa" nello spazio. Se
osserviamo la figura qui a lato ci rendiamo facilmente conto che, per chi vive sulla sfera, la
circonferenza evidenziata ha centro nel punto A e i suoi "raggi" sono quelli indicati (li chiameremo
raggi intrinsechi). A differenza di quanto succede nel piano, però, il centro potrebbe essere anche il
punto B diametralmente opposto ad A, ed in questa diversa visione anche i raggi cambiano
opportunamente.
Per chi può guardare le cose dallo spazio, la stessa circonferenza ha un unico centro, diverso sia da
A che da B, e situato sul piano che contiene la circonferenza stessa. Anche il raggio che si misura
da questo punto di vista è diverso (lo potremmo chiamare raggio estrinseco). Non è difficile
rendersi conto, anche a livello intuitivo, che, in generale, gli archi di queste circonferenze non sono
i cammini più brevi tra due loro punti.
E' anche evidente che le circonferenze
tracciate sulla sfera non possono avere raggi intrinsechi arbitrariamente grandi e che anzi le
circonferenze più grandi sono quelle che hanno raggio estrinseco uguale al raggio della stessa sfera
e quindi raggio intrinseco uguale a πr/2: in questo caso, pur continuando le circonferenze ad avere
due possibili centri, hanno un unico raggio. Queste circonferenze sono dette circonferenze massime
o cerchi massimi. Esse sono, come è facile provare, e come è intuitivamente evidente, le geodetiche
della sfera: dati due punti A e B, non diametralmente opposti, esiste un unico cerchio massimo che
passa per entrambi, e il più piccolo dei due archi di questo cerchio individuati da A e B rappresenta
la linea di minima distanza tra A e B. Se i punti sono diametralmente opposti di cerchi massimi
passanti per A e B ce ne sono infiniti e la distanza tra A e B misurata lungo uno qualunque di essi è
πr.
E' interessante osservare anche che, dati due punti A e B sulla sfera, non diametralmente opposti, e
il cerchio massimo che passa per entrambi, i due archi individuati sul cerchio da A e B, pur avendo
diversa lunghezza, possono entrambi essere considerati "linee diritte" che congiungono i punti. Un
essere bidimensionale che parta da A cercando di muoversi "in linea retta" verso B, può
indifferentemente seguire uno dei due versi: raggiungerà comunque B. Questo fatto è
essenzialmente legato alla "limitatezza" della sfera, che la differenzia dal piano.
Per concludere osserviamo esplicitamente che, se si considerano due punti diametralmente opposti
sulla sfera e due semicerchi massimi (due "meridiani") che li colleghino, si viene a costruire una
figura interessante che non ha paragoni sul piano: un "poligono" (lo possiamo chiamare così perché
i suoi lati sono linee "rette") formato da due soli lati. La cosa è sorprendente perché nel piano
nessun poligono limitato può avere meno di tre lati.
Una volta introdotto il concetto di geodetica, cioè di "linea diritta",
sulla sfera possiamo costruire le altre figure tradizionali della geometria e chiederci che cosa
succede delle usuali proprietà a cui siamo abituati sul piano.
Nella figura qui a lato è rappresentato un triangolo costruito utilizzando tre archi di cerchio
massimo: si potrebbe provare che qualunque triangolo si costruisca, la somma dei suoi angoli
interni è sempre maggiore di 180°, ma questo è argomento della geometria sferica ed esula dagli
scopi di questa introduzione al concetto di geodetica.
In ogni caso è importante ripetere che, per chi vive sulla sfera, non c'è alcuna differenza tra questo
triangolo e quello che non siamo abituati a vedere nel piano: è solo la straordinaria circostanza che
ci permette di guardare le cose da una dimensione superiore, cioè di uscire dalla sfera o dal piano
della geometria di Euclide, che ci fa vedere queste situazioni come diverse.
Le immagini qui sotto mostrano tre esempi di archi di geodetica sulla sfera. La prima immagine è la
linea più breve tra Napoli e New York, che si trovano sullo stesso parallelo: la geodetica non
coincide con il parallelo. La seconda immagine collega due punti più vicini al Polo Nord: la
geodetica è notevolmente distante dal parallelo. La terza immagine mostra invece due punti
sull'equatore: la geodetica è l'equatore stesso, che è un cerchio massimo.
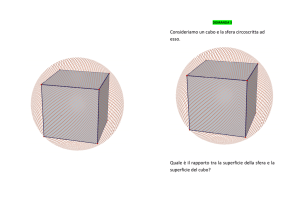
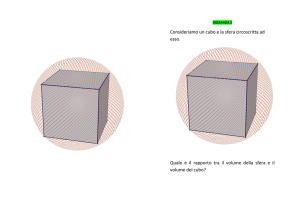
Geodetiche sul cubo
Se sostituiamo la sfera con un cubo potremo fare qualche ulteriore interessante osservazione
derivata dal concetto di linea più breve tra due punti.
Intanto possiamo cominciare con l'osservare che per due punti che stanno su una stessa faccia la
linea di minima distanza è sicuramente il segmento ordinario tra i due punti.
Per trattare il caso di due punti che stanno su
facce contigue basta pensare di sviluppare il cubo su un piano. La figura a lato mostra che la
distanza minima tra i due punti quando le facce sono sviluppate su un piano è il segmento AB, e che
questo forma con lo spigolo ON due angoli uguali. Una volta ripiegate le facce per ricostruire il
cubo, poiché naturalmente le lunghezze non variano, il percorso di minima distanza deve continuare
a mantenere gli angoli uguali: è questa la regola che devono seguire le geodetiche per passare da
una faccia ad una adiacente. Ci si può chiedere, a questo punto, se un essere bidimensionale che si
muove lungo la geodetica, si accorge oppure no della presenza dello spigolo. La risposta è no: la
linea ON, che per noi che vediamo il cubo immerso nello spazio ha un significato speciale, per chi
sta sulla superficie ha esattamente lo stesso valore di una qualunque altra linea ad essa parallela
tracciata su una delle due facce. Infatti ciò che conta è che gli angoli tra il tragitto AB e una di
queste linee siano uguali (in quanto opposti al vertice).
Chiediamoci ora come appaiano le "circonferenze" sul cubo. La cosa è
molto facile se consideriamo circonferenze con raggio tale da non uscire da una faccia: saranno le
ordinarie circonferenze del piano. Negli altri casi basterà agire come prima, sviluppando il cubo e
poi ripiegandolo.
Non è difficile rendersi conto intuitivamente delle figure che si possono ottenere e che, tutto
sommato, non sono sostanzialmente diverse dalle ordinarie circonferenze del piano.
Nella figura qui a lato abbiamo considerato tre diversi esempi, di cui uno tratta il caso di centro su
un vertice del cubo.
Vogliamo ora provare a costruire poligoni, cioè figure chiuse delimitate da "segmenti", ovvero parti
di geodetica. Naturalmente, come nel caso delle circonferenze, saranno interessanti solo le figure
che non hanno tutti i lati su una faccia, dove le cose vanno come nell'ordinario piano di Euclide.
Cominciamo a considerare la linea chiusa rappresentata in rosso nella
figura qui a lato: a chi la guarda dallo spazio tridimensionale, appare essere un quadrato ottenuto
per sezione del cubo con un piano. A chi vive sul cubo invece la linea appare come una linea
continua senza alcun vertice (ricordiamo che non è possibile apprezzare la presenza degli spigoli del
cubo, senza "uscire" dal cubo stesso): si tratta di un poligono chiuso con un solo lato!
Notiamo che i contorni delle facce del cubo, che per noi sono identiche al monogono precedente,
sono invece intrinsecamente diverse: in questo caso anche chi sta sul cubo può apprezzare la
presenza dell'angolo tra due spigoli della stessa faccia.
Per chi sta sul cubo il
bordo di una faccia è un quadrato esattamente come quello che uno potrebbe tracciare all'interno di
una faccia (vedi, nella figura a lato, il rettangolo interno alla faccia superiore). Per rendersi conto
ancora meglio del fatto che questa linea ha, vista dal cubo, un solo lato, si può pensare di sviluppare
il cubo, in modo che le quattro facce interessate siano adiacenti una all'altra: il quadrato si sviluppa
in un segmento.
Esistono anche altri monogoni sul cubo: l'esempio più semplice è l'esagono della figura qui a lato,
ottenuto congiungendo i punti medi di sei spigoli.
Anche sul cubo, come sulla sfera, si possono poi tracciare poligoni con due lati. Basta esaminare la
figura qui a sinistra, che non è, nella sostanza, molto diversa da quella che abbiamo indicato sulla
sfera (un "bigono" che ha come vertici due punti diametralmente opposti e come lati due meridiani
passanti per quei punti).
Proseguendo con il numero dei lati, ci si può chiedere come sono i triangoli tracciati
su un cubo. In generale non è difficile rendersi conto intuitivamente di come vanno le cose, magari
ragionando sullo sviluppo piano del cubo. Ci sono anche alcune situazioni interessanti (e
sorprendenti) come quella del triangolo equilatero tracciato qui a lato.
Geodetiche su altre superfici
In generale su superfici più complesse le linee geodetiche sono curve
più difficili da descrivere. Fanno eccezione le superfici che si possono sviluppare su un piano, come
i cilindri e i coni: in questo caso si potrà, dati due punti sulla superficie, svilupparla sul piano,
tracciare il segmento che unisce i due punti, e successivamente ricostruire la superficie di partenza.
Ci sono comunque alcune difficoltà, anche nel semplice caso del cilindro, di cui ci si può rendere
conto esaminando la figura qui a lato. Immaginiamo di arrotolare il rettangolo LMNP, facendo
coincidere i lati LP ed MN: i punti B e B' andranno a coincidere. Ora nel rettangolo i segmenti AB
e AB' sono entrambi "rettilinei", ma connettono due punti distinti. Dopo l'arrotolamento essi
dovranno continuare ad essere considerati "rettilinei", ma connetteranno lo stesso punto. E' ovvio
che solo uno dei due sarà il cammino più breve tra A e B sul cilindro, ma, poichè entrambi avranno
i titoli per essere chiamati "diritti", potremo concludere che tra i due punti potranno passare due
distinte "rette". La cosa è in realtà ancora più complessa: esaminando di nuovo la figura qui a lato ci
possiamo rendere conto che il percorso AC'+CB', che a noi appare "diritto", ma spezzato, sul
cilindro apparirà ancora "diritto", ma questa volta non più spezzato e collegherà ancora i due punti
A e B. Dati due punti esistono, in generale, infinite "rette" distinte che passano per entrambi (fanno
eccezione i punti che si trovano su una circonferenza ottenuta sezionando il cilindro con un piano
perpendicolare all'asse). Le curve del tipo di quelle tracciate si chiamano eliche circolari. La
"distanza verticale" tra due "spire" di una di queste curve si chiama passo dell'elica. Il segmento
verticale si usa interpretare come un'elica di passo infinito, mentre le circonferenze ottenute per
sezione con un piano "orizzontale" sono eliche di passo zero.
Insomma: estendere il concetto di "linea retta", così usuale e apparentemente semplice nel piano,
ad altre superfici, non è poi una cosa tanto banale!
Bibliografia per questa pagina


http://users.libero.it/prof.lazzarini/geometria_sulla_sfera/geo01.htm (Da questo bellissimo
ipertesto, completo di animazioni, abbiamo preso parecchie idee inserite in questa pagina.
Consigliamo anche la visita di un altro ipertesto, collegato a questo, su
http://users.libero.it/prof.lazzarini/geometria_sulla_sfera/modelli_noneuclidei.htm).
http://www.dm.unibo.it/matematica/GeometrieNonEuclidee/indice.html
Capitolo N
pagina pubblicata il 18/03/2004 - ultimo aggiornamento il 18/03/2004