Studio del grafico di una funzione. Attività 1
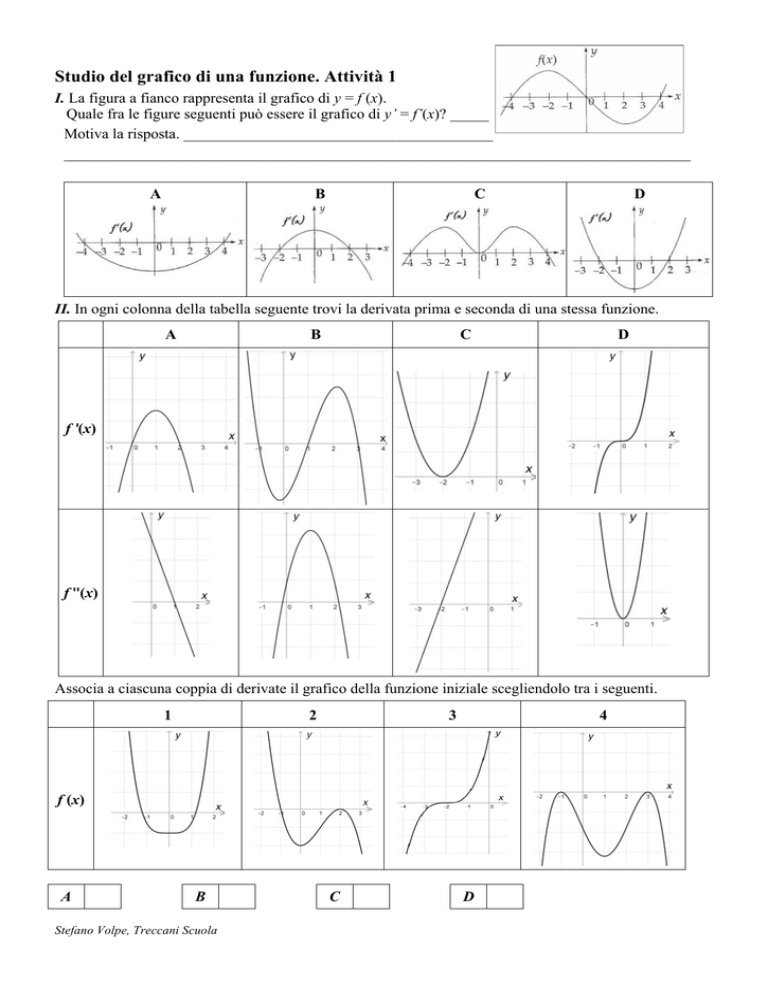
I. La figura a fianco rappresenta il grafico di y = f (x).
Quale fra le figure seguenti può essere il grafico di y’ = f’(x)? _____
Motiva la risposta. ________________________________________
_________________________________________________________________________________
A
B
C
D
II. In ogni colonna della tabella seguente trovi la derivata prima e seconda di una stessa funzione.
A
B
C
D
f '(x)
f ''(x)
Associa a ciascuna coppia di derivate il grafico della funzione iniziale scegliendolo tra i seguenti.
1
2
3
4
f (x)
A
B
Stefano Volpe, Treccani Scuola
C
D
III. Completa il procedimento per tracciare il grafico di y =
1 4
x − 2x 2 .
4
1. Prime caratteristiche del grafico
− Qual è l’insieme di definizione della funzione? _____________
− La funzione è pari o dispari? _________________
€
2. Completa lo studio del segno della funzione e riassumi i risultati nello schema a fianco.
- Scrivo la funzione come prodotto di due funzioni di 2° grado.
1
y = x 2 (.............)
4
1
- Studio il segno dei fattori F1 = x 2
F2 = ............
4
- Per ricavare il segno del prodotto y tengo presente che:
€ • y = 0 se almeno un fattore è zero;
• y > 0 se i fattori hanno segno concorde;
€ hanno segno discorde.
• y < 0 se i fattori
3. Calcola la derivata y’ = f’(x), studiane il segno e riassumi i risultati nello schema a fianco
y’ = ___________________________
- Scrivo la derivata come prodotto di due funzioni.
y' = x (..............)
- Studio il segno dei fattori F3 = x
F4 = ............
- Ricavo il segno del prodotto y’.
€4. Calcola la derivata y” = f”(x)
y” = _______________________
€
Studia segno di y” e descrivilo nello schema a fianco
5. Riassumi qui sotto in un unico schema (a sinistra) il segno della funzione e delle sue derivate.
6. Elenca qui sotto i punti notevoli (intersezioni con asse x, massimi o minimi relativi, flessi) e
determinane le ordinate. Scrivi l’elenco dei punti sotto lo schema riassuntivo del segno.
7. Nel piano cartesiano a destra disegna infine il grafico della funzione assegnata a partire da tutte le
informazione che hai ottenuto.
Spiega come puoi basarti sulla simmetria per disegnare più rapidamente il grafico.
_____________________________________________________________________________
Stefano Volpe, Treccani Scuola










