1
GENERALITÀ
Abbiamo visto che con le ruote di frizione si hanno dei limiti nella trasmissione di potenze
potenz
elevate a causa delle proibitive sollecitazioni radiali cui devono essere sottoposte per garantire
garantir
l'aderenza.
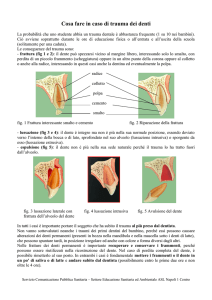
Fig. 1 – Principio di funzionamento
mento delle ruote dentate
dentat
A partire d a due ruote di frizione ideali, rappresentate dalle circonferenze tratteggiate nella
fig.1, immaginiamo di ricavare sulle loro superfici
superfici esterne una serie di denti alternati a spazi
vuoti, che durante il moto si compenetrano
compenetrano facilmente;
è evidente come, in tal caso, la
trasmissione della potenza non è più affidata all'attrito,
all'attrito ma alla spinta che ciascun dente della
ruota motrice esercita su quelli della ruota condotta. In
In tal modo, purché si costruiscano
costruisca denti
sufficientemente
ficientemente robusti, sarà possibile trasmettere potenze anche grandi.
Si definisce INGRANAGGIO un meccanismo composto da due ruote dentate,
dentate una delle quali
(motrice) trasmette il moto all'altra (condotta).
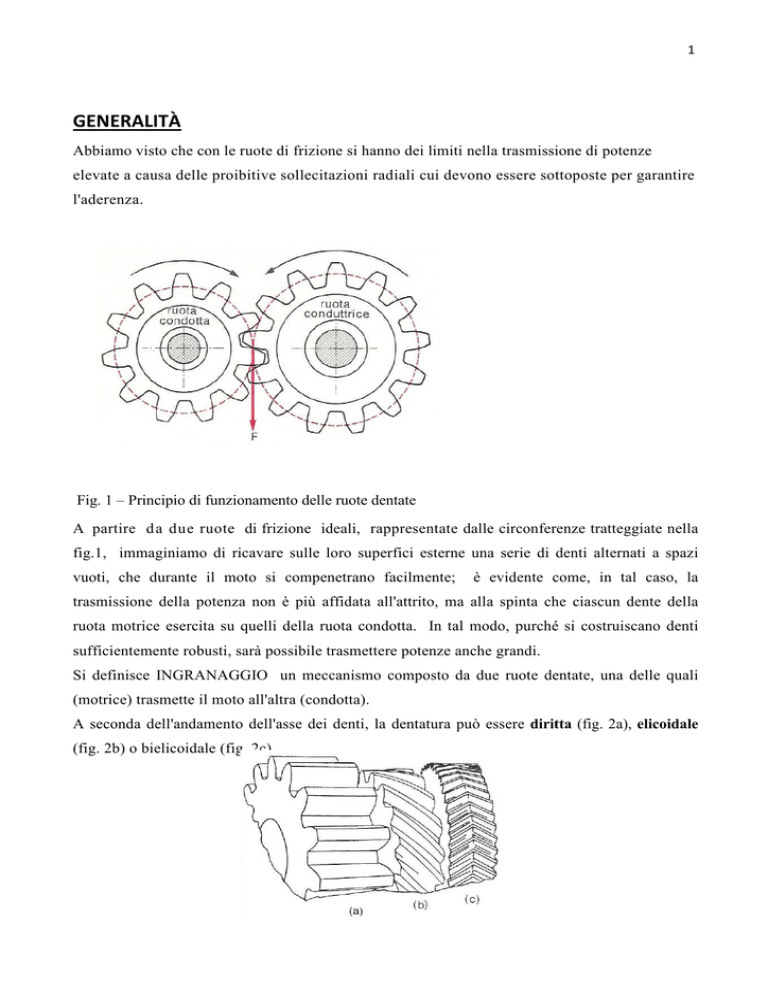
A seconda dell'andamento dell'asse dei denti, la dentatura può essere diritta (fig. 2a), elicoidale
(fig. 2b) o bielicoidale (fig. 2c)
2
Con gli ingranaggi si può trasmettere il moto, oltre che tra due alberi con assi paralleli (con ruote
cilindriche a denti diritti e a denti elicoidali), anche
anch tra alberi ad assi concorrenti (fig. 3:
3
Fig. 3 – Ruote coniche
utilizzando ruote coniche sia a denti diritti che elicoidali), tra alberi ad assi sghembi
(fig. 4a:
con ruote a denti elicoidali; fig. 4b: con coppie di ingranaggi conici; fig. 4c:
4c: con meccanismo vite
senza fine ruota elicoidale.
3
Fig. 4 - Trasmissione tra assi sghembi: a) con ruote a denti elicoidali; b) con coppie di ingranaggi
conici; c) con meccanismo vite senza fine/ruota elicoidale
Inoltre è possibile operare la trasformazione del moto da rotatorio a traslatorio con il meccanismo
pignone/cremagliera (fig. 5).
4
CARATTERISTICHE DELLA DENTATURA
DENTATUR
Elementi caratteristici di una ruota dentata
•
CIRCONFERENZA DI TESTA : è la circonferenza che limita la sommità dei denti.
•
CIRCONFERENZA PRIMITIVA : è la circonferenza lungo al quale avviene il contatto
della coppia di ruote dentate :
•
CIRCONFERENZA DI FONDO : è la circonferenza che limita la base dei denti.
•
PASSO (P)
P) : è la lunghezza dell'arco di circonferenza primitiva compresa tra gli assi di due
denti consecutivi.
•
SPESSORE (S) : è la lunghezza dell'arco di circonferenza primitiva delimitata da un dente.
•
VANO (V): è la lunghezza dell’arco di circonferenza primitiva
primitiva compresa tra due denti
consecutivi.
•
LARGHEZZA: è la larghezza della parte dentata della ruota.
5
•
ALTEZZA (h): è la distanza misurata lungo il raggio fra la circonferenza di testa e quella di
fondo.
•
COSTA: è la parte del dente compresa tra la circonferenza primitiva e quella di testa.
•
FIANCO: è la parte del dente compresa tra la circonferenza di fondo e quella primitiva.
•
ADDENDUM (add): è l’altezza della testa del dente.
•
DEDENDUM (ded): è l’altezza della base del dente.
Indicando con dp il diametro della circonferenza primitiva e con z il numero dei denti, per ogni
ruota dentata vale la seguente relazione per il calcolo del passo:
P=
π *dP
z
In cui :
π * dP
(rappresenta la lunghezza della circonferenza primitiva );
z (rappresenta il numero di denti).
Il Passo, precedentemente definito, è un elemento caratteristico della dentatura che un tempo veniva
utilizzato come riferimento per il dimensionamento di tutte le altre parti della ruota dentata.
Tuttavia il Passo presenta l’inconveniente di essere un numero con la virgola in quanto affetto della
irrazionalità del
π.
Allora è stato introdotto un nuovo parametro, caratterizzante per le ruote
dentate, chiamato modulo (m) espresso in mm.
m=
In cui
dP
z
d P = lunghezza del diametro primitivo; z = numero di denti.
Sostituendo la relazione che esprime il modulo (m)
p = π *m
da cui si ricava
m=
m=
dP
z
nella p =
π * dP
z
si ottiene che
p
π
Due ruote ingrananti tra di loro hanno lo stesso passo e quindi lo stesso modulo.
L’altezza dell’ ADDENDUM (add.) è pari al modulo (m), mentre l’altezza del DEDENDUM è
pari ad 1,25 volte il modulo (1,25 * m) .
Poiché l’altezza del dente non è altro che la somma tra l’altezza dell’ADDENDUM e l’altezza
del DEDENDUM :
ADDENDUM + DEDENDUM = m + 1,25 *m = m*(1+1,25) = 2,25 *m
6
Il diametro esterno chiamato anche diametro di testa si calcola con la relazione
d ( Testa ) = d (Pr imitivo ) + 2 * addendum = d (Pr imitivo ) + 2 * m
Il diametro interno chiamato anche diametro di piede si calcola con la relazione
d ( Piede ) = d (Pr imitivo ) − 2 * dedendum = d (Pr imitivo ) − 2 * 1, 25 * m
La larghezza della dentatura si calcola si indica con (b) e si calcola con :
b = (8 ÷ 12) * m
Lo spessore del dente si calcola con :
S =π *
m
2
7