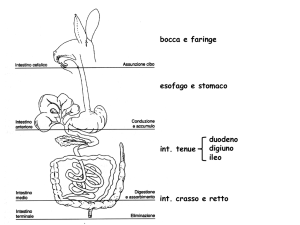
UdA n. 2: “Controllo dimensionale di un elemento esterno
(dente) di un organo meccanico (ingranaggio) prodotto in serie”
Classe 4^Am
Sottogruppo n° 5: Da Ros Lorenzo, Facchin Damiano, Zanchetta Edoardo
Relazione
Controllo della dentatura mediante micrometro a piattelli: problematiche
Durante lo svolgimento dell’UdA abbiamo inizialmente ipotizzato di poter eseguire il controllo
della dentatura seguendo il percorso di verifica di una ruota dentata a denti diritti.
Usualmente si ricorre al metodo di seguito illustrato che prevede
l’ausilio di una tabella come quella a lato.
Controllo della ruota a denti diritti con il micrometro a
piattelli:
per prima cosa ci si ricava mediante la tabella il numero
di denti da comprendere tra i piattelli del micrometro durante le
misurazioni (per 27 denti ed α = 20° si ha z = 4);
dalla tabella si assume il dato teorico dello scartamento
(nel caso di modulo 2 è Wt = 10,7106 * 2 = 21,42 mm);
si effettuano varie misurazioni e si calcola il valore medio
Wm;
si dà un giudizio di idoneità alla ruota se lo scartamento
Wm é compreso tra:
Wmax = Wt – (g/2) + t
Wmin = Wt – (g/2) – t
Con “g” il giuoco tra I fianchi dei denti e “t” la tolleranza sullo spessore cordale.
Ciò ha determinato dei risultati diversi da quelli indicati dall’azienda “Nuova Trasmissione”
(azienda fornitrice dei campioni di ruote), in quanto la dentatura delle nostre ruote é
elicoidale.
Abbiamo allora utilizzato un
metodo specifico per le ruote a
denti elicoidali, che hanno 3
passi:
- passo normale
- passo trasversale
- passo assiale
Quindi si hanno anche 3
moduli.
La ruota fornita dall’azienda ha:
- modulo normale mn = 2
- inclinazione dell’elica
β = 3° 22’ 35’’
- passo normale pn = 6,28
Il metodo di controllo utilizzato
prevede:
1) determinazione del valore dell’angolo di pressione trasversale:
tg αt = (tg αn) / (cos β)
2) calcolo del numero dei denti Z’ da prendere tra i piattelli:
Z’ = Z · (αt / 180) + 0,5
3) calcolo della funzione (tg αt - αt)
(tg αt - αt) = 0.364603 – (3,14·20.03°/180)
4) determinazione della corda primitiva teorica (scartamento) Wt:
Wt = mn · cos αn [(Z’ – 0,5) 3.14 + Z(tg αt - αt ]
6) determinazione degli scostamenti tollerati
Wmax = Wt – (g/2) + t
Wmin = Wt – (g/2) – t