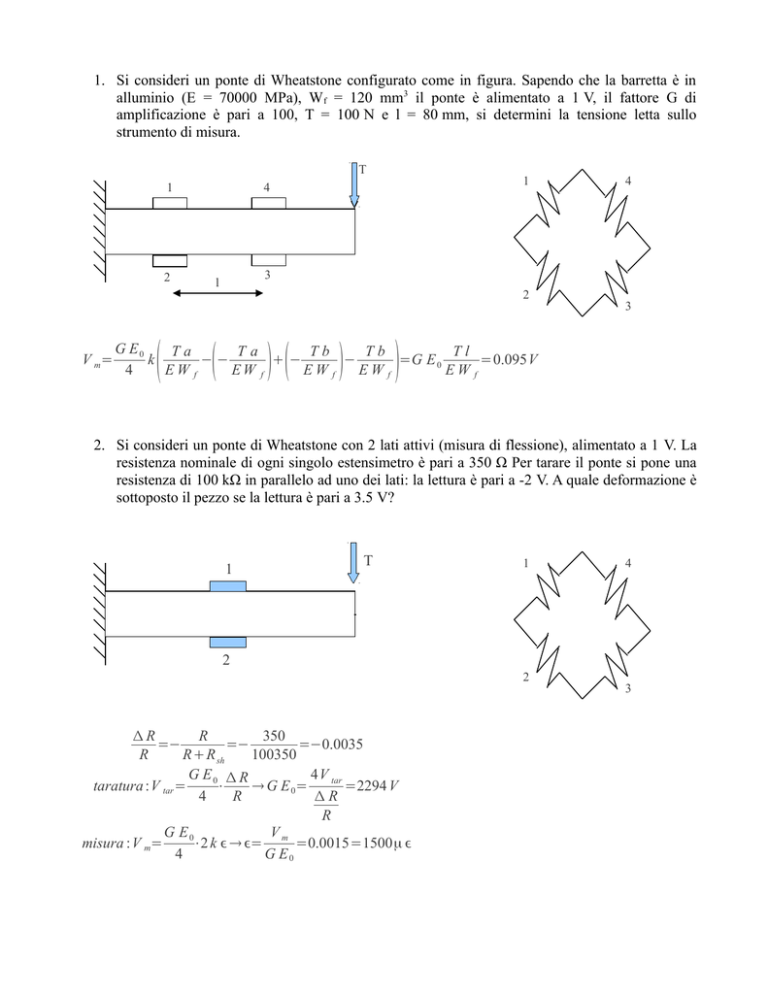
1. Si consideri un ponte di Wheatstone configurato come in figura. Sapendo che la barretta è in
alluminio (E = 70000 MPa), W f = 120 mm3 il ponte è alimentato a 1 V, il fattore G di
amplificazione è pari a 100, T = 100 N e l = 80 mm, si determini la tensione letta sullo
strumento di misura.
T
1
2
V m=
1
4
4
3
l
2
3
G E0
Ta
Ta
Tb
Tb
Tl
k
−−
+−
−
=G E 0
=0.095V
4
EW f
EW f
EW f
EW f
EW f
(
(
)(
)
)
2. Si consideri un ponte di Wheatstone con 2 lati attivi (misura di flessione), alimentato a 1 V. La
resistenza nominale di ogni singolo estensimetro è pari a 350 Ω Per tarare il ponte si pone una
resistenza di 100 kΩ in parallelo ad uno dei lati: la lettura è pari a -2 V. A quale deformazione è
sottoposto il pezzo se la lettura è pari a 3.5 V?
1
T
1
4
F
2
2
ΔR
R
350
=−
=−
=−0.0035
R
R+R sh
100350
G E0 Δ R
4V tar
taratura :V tar =
⋅
→ G E 0=
=2294 V
4
R
ΔR
R
G E0
Vm
misura :V m=
⋅2 k ϵ → ϵ=
=0.0015=1500μ ϵ
4
G E0
3
3. Sia una trave di alluminio (E = 70000 MPa) soggetta ad un’azione di compressione pari a
100 N; tale trave ha una sezione rettangolare la cui base è pari a 20 mm e l’altezza a 0.5 cm. La
misura è effettuata utilizzando una configurazione a mezzo ponte (2 estensimetri attivi, k=2),
alimentato a 1 V. Sapendo che la taratura ha evidenziato la presenza di un fattore di
amplificazione G = 1000 fra sbilanciamento del ponte e tensione letta, si indichi quale sarà il
valore di tensione letto sul voltmetro.
1
1
4
F F
3
2
V m=
3
G E0
F
100
2k
=1000⋅
=0.0143V
4
EA
70000⋅100
4. Si consideri un ponte di Wheatstone per misure estensimetriche con 4 lati attivi (misura di
flessione). La resistenza nominale di ogni singolo estensimetro è di 350 Ω, kest=2. Per tarare il
ponte si utilizza una resistenza in parallelo ad uno dei lati di 120 kΩ. Sul display si legge una
tensione pari a -3 V. A quale deformazione è sottoposto il pezzo se la lettura è pari a 3.5 V?
1
1+3
F
4
Mf
2+4
2
ΔR
R
350
=−
=−
=−0.0029
R
R+R sh
120350
G E0 Δ R
4V tar
taratura :V tar =
⋅
→ G E 0=
=4138 V
4
R
ΔR
R
G E0
Vm
misura :V m=
⋅4 k ϵ → ϵ=
=423μ ϵ
4
k G E0
3
5. Si voglia misurare la deformazione ottenuta da un’azione di trazione mediante un ponte
estensimetrico con quattro lati attivi. Si posizionino correttamente gli estensimetri sulla barra.
Tutte le resistenze del ponte hanno un valore nominale di 120 Ω. In fase di taratura è stata
utilizzata una resistenza di calibrazione di 10 kΩ, alla cui applicazione in parallelo ad un lato
del ponte è corrisposta una lettura pari a -3 V. Sapendo che il ponte è alimentato a 1 V, si
determini la deformazione della barra che corrisponde ad una tensione letta di 100 mV.
2
1
1
4
F
F
4
3
2
3
ΔR
R
120
=−
=−
=−0.0119
R
R+Rsh
10120
G E0 Δ R
4V tar
taratura:V tar =
⋅
→ G E 0=
=1012V
4
R
ΔR
R
G E0
Vm
misura :V m=
⋅2 k (1+ν) ϵ → ϵ=
=76 μ ϵ
4
1.3G E 0
6. Una trave di sezione rettangolare (base = 0.2 dm, altezza = 5 mm) in alluminio
(E = 70000 MPa) è sollecitata mediante una forza di taglio applicata al suo estremo non
vincolato. Per valutare la forza applicata si utilizza un opportuno ponte estensimetrico,
configurazione mezzo ponte, i cui estensimetri hanno una resistenza nominale pari a 120 Ω e
k = 2. In fase di taratura viene utilizzata una resistenza di shunt di 120 kΩ e la lettura
corrispondente è pari a -2.2 V.
•
•
•
•
Si indichi la posizione degli estensimetri sulla trave e nel collegamento elettrico.
Si valuti il valore della forza applicata sapendo che la tensione letta è pari a 3.0 V e il
braccio della forza (x nella soluzione) è pari a 20 mm.
Si valuti la sensibilità del ponte utilizzato come trasduttore di forza.
Si valuti se sono compensati gli effetti della temperatura. In caso negativo si suggerisca
almeno un modo per procedere alla compensazione.
1
1
T
4
F
2
2
ΔR
R
120
=−
=−
=−0.001
R
R+R sh
10120
G E0 Δ R
4 V tar
taratura : V tar =
⋅
→ G E0=
=8800 V
4
R
ΔR
R
2
bh
W f=
=83.3 mm3
6
G E0
EW f
Tx
misura :V m=
⋅2 k
→ T =V m
=99.4 N
4
EW f
G E0 x
V
G E0 x
V
S= m=
=0.03
T
EW f
N
Gli effetti della temperatura sono compensati
3