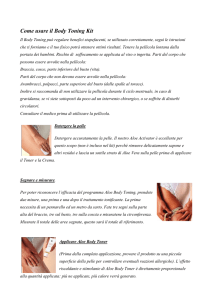
Sia R il raggio della sfera che rappresenta il mappamondo. Rappresentiamo la
geometria del contenitore,sapendo che il suo raggio di base è r e l’altezza è h.
I dati sono
Poniamo
Si ha che
Con
Da cui
Ma è
Inoltre
Da cui
Calcoliamo l’area della superficie laterale del cono con la formula
E quindi
E quindi
E quindi
Posto
La funzione diventa
Con
In questo intervallo la funzione è continua.
Calcoliamo la derivata
Quindi
Da cui
Ossia
E quindi
se e solo se
L’equazione associata è
Da cui
E quindi
Da cui risulta che t=-1 è un punto di massimo e
è il minimo. Quindi
Da cui
E
Da cui
E
La prima pellicola perde ogni anno il 3% della resistenza iniziale all’usura
Indicando con
Quindi
la resistenza iniziale all’usura si ha la seguente equazione ricorsiva
E quindi, analogamente, la pellicola che perde ogni anno il 5% avrà modello
Imponendo che
si ottiene
Cioè
Da cui
E quindi,la prima pellicola dovrà essere sostituita quando
Mentre la seconda pellicola dovrà essere sostituita quando
È chiaro che la prima pellicola è più vantaggiosa