Formato PDF

CAPITOLO 1
Equazione di Schrödinger in una dimensione. Problemi.
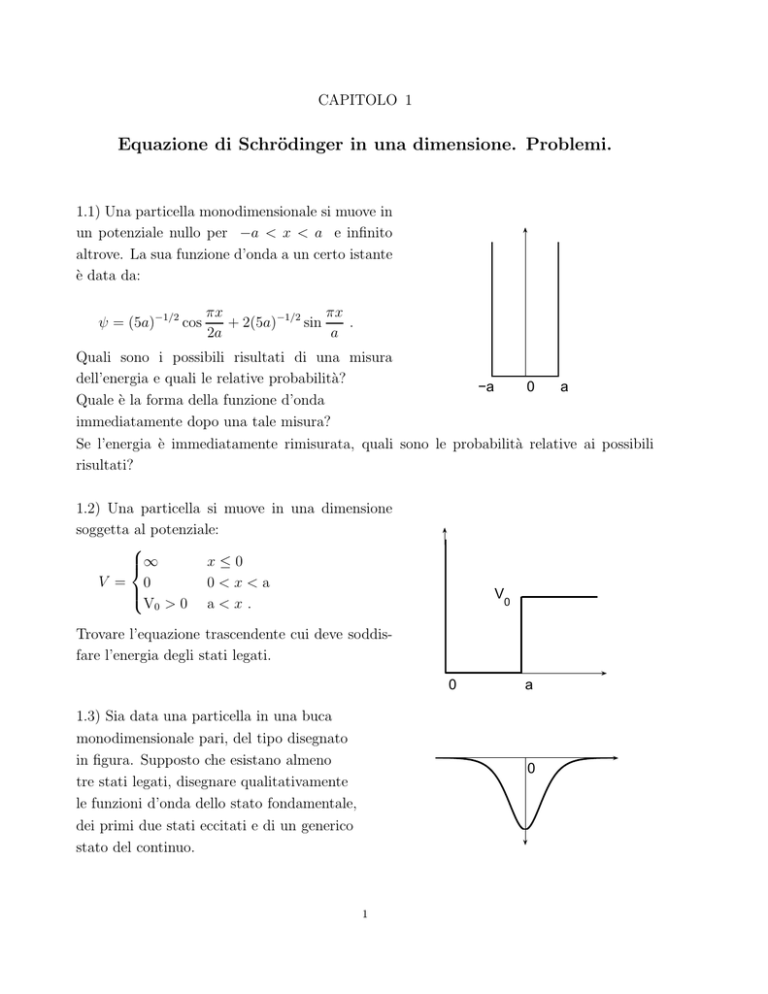
1.1) Una particella monodimensionale si muove in
un potenziale nullo per −a < x < a e infinito
altrove. La sua funzione d’onda a un certo istante
è data da:
ψ = (5a)−1/2 cos
πx
πx
+ 2(5a)−1/2 sin
.
2a
a
Quali sono i possibili risultati di una misura
dell’energia e quali le relative probabilità?
−a
0
a
Quale è la forma della funzione d’onda
immediatamente dopo una tale misura?
Se l’energia è immediatamente rimisurata, quali sono le probabilità relative ai possibili
risultati?
1.2) Una particella si muove in una dimensione
soggetta al potenziale:


x≤0
∞
V = 0
0<x<a

V > 0 a < x .
0
V
0
Trovare l’equazione trascendente cui deve soddisfare l’energia degli stati legati.
0
1.3) Sia data una particella in una buca
monodimensionale pari, del tipo disegnato
in figura. Supposto che esistano almeno
tre stati legati, disegnare qualitativamente
le funzioni d’onda dello stato fondamentale,
dei primi due stati eccitati e di un generico
stato del continuo.
a
0
1
2
1. EQUAZIONE DI SCHRÖDINGER IN UNA DIMENSIONE. PROBLEMI.
1.4) Per una barriera di potenziale V (x) sono
note le ampiezze di riflessione e di trasmissione
{ρ(k), τ (k)}.
Discutere l’effetto tunnel nel caso di
due barriere V (x) poste a distanza L .
1.5) Si consideri
a tratti):

∞



−V
0
V =

V1



0
V(x)
V(x)
L
il seguente potenziale (costante
x≤0
0<x<a
a < x < a+b
a+b<x ,
V1
0
a
a+b
dove tutte le costanti V0 , V1 , a, b sono positive.
−V0
i) Descrivere qualitativamente lo spettro
dell’Hamiltoniana H = p2 /2µ + V (x).
Discutere il caso limite V1 → ∞ .
ii) Risolvere l’equazione di Schrödinger agli stati stazionari e ricavare una equazione trascendente cui soddisfano gli autovalori dell’energia.
iii) Attraverso considerazioni semiclassiche (WKB) ottenere una condizione approssimata
per l’esistenza di almeno uno stato legato per a = 1.0Å e µ = 0.511MeV/c2 . (Si
rammenti che ~c ∼ 197MeVf m ).
1.6) Sia data una particella monodimensionale di massa
µ immersa nel potenziale:


∞
x≤0


V =


− λ 0 < x .
x
0
Determinare autovalori e autofunzioni con il metodo
dello sviluppo in serie.
√
Posto k = −2µW /~ , x0 = ~2 /(λµ) , b = 1/(kx0 ),
ξ = 2kx , sviluppare in serie la funzione u(aξ)
definita da ψ(x) = Ae−ξ/2 u(ξ) , con A costante di normalizzazione.
1.7) Discutere sia qualitativamente che quantitativamente lo spettro discreto del potenziale:
V (x) = −V0 e−|x|/a , con V0 e a costanti reali positive. (Cfr. il 1.8).
1. EQUAZIONE DI SCHRÖDINGER IN UNA DIMENSIONE. PROBLEMI.
1.8) Trovare l’energia e la funzione d’onda dello stato fondamentale di una particella
monodimensionale immersa nel campo:
3
0
V (x) = −V0 e−|x|/a
−V
Studiare in particolare il caso di una buca con
µa2 V0 /~2 1, sfruttando la relazione:
Jν0 (λ) ≈
ν
1
(λ/2)ν−1 −
(λ/2)ν+1
2Γ(ν + 1)
Γ(ν + 2)
0
λ 1.
(Cfr. A-S 9.1.7 e 9.1.27).
1.9) Determinare (implicitamente) autovalori
e autofunzioni di una particella soggetta
al potenziale:
V =
(
−λx
1/2 µω 2 x2
x≤0
0≤x.
0
1.10) Una particella si muove in una dimensione sotto
l’azione di forze aventi energia potenziale:


V1
V = −V0

0
|x| < a
a < |x| < b
b < |x| ,
V1
−b −a
0
a
b
−V
0
con a, b, V0 , V1 costanti positive. Si discutano le proprietà qualitative dello spettro di energia. Si trovi l’equazione che determina lo spettro per gli stati a parità −1, cioè tali che la
relativa autofunzione soddisfi ψ(−x) = −ψ(x).
1.11) Una particella di massa µ = 0.5 MeV/c2
V0
con energia W = 1 eV incide su una barriera di
W
potenziale di altezza V0 = 2 eV. Quanto deve
0
a
essere larga la barriera affinchè la probabilità di
trasmissione sia pari a 10−3 ? Per ottenere una probabilità cosı̀ piccola, la barriera
deve essere molto larga, e dunque si può considerare una riflessione quasi totale al primo
gradino, seguita da un ordinario fenomeno di riflessione e trasmissione al secondo.
4
1. EQUAZIONE DI SCHRÖDINGER IN UNA DIMENSIONE. PROBLEMI.
1.12) Consideriamo il seguente potenziale semiperiodico, cioè periodico a destra con barriera infinita
all’origine:


x≤0
∞
V = 0
2nL < x < (2n + 1)L

V
(2n + 1)L < x < (2n + 2)L
0
V
0
con L e V0 costanti positive, e n = 0, 1, 2, ... .
Dimostrare che esistono stati legati con
0 L 2L 3L 4L 5L
energia W per la particella quantistica
in corrispondenza alle soluzioni dell’equazione: k cot(kL) = −χ coth(χL) , dove
p
√
k = 2µW /~ e χ = 2µ(V0 − W )/~ . Discutere il problema degli autovalori dell’energia
nel caso in cui le barriere di potenziale V0 siano in numero finito, ossia V (x) = 0 per
x > 2N L , per qualche N intero positivo. [Per il primo quesito, provare a imporre la
condizione ψ(2L) = 0 ; giustificare questa ulteriore condizione sulla funzione d’onda in
base alla teoria dei potenziali periodici.]
1.13) Determinare il coefficiente di trasmissione di
una barriera di potenziale della forma:

x<0

0
V =

V (1 − x ) 0 < x ,
0
a
V0
0
a
con V0 > 0 e a > 0 .
[ Operare la sostituzione: y = ( 2µV0 /(a~2 ) )1/3 ( x − a + a W /V0 ) ] .
1.14) Una particella si muove in una dimensione
sotto l’azione di forze aventi energia potenziale:


|x| < a
V0
V = 0
a < |x| < b

+∞ b ≤ |x| ,
V
0
con a, b, V0 costanti positive.
Si trovi l’equazione che determina lo spettro,
tenendo conto della simmetria del potenziale.
−b
−a
0
a
b
Assumendo che la funzione d’onda iniziale sia:
ψ0 (x) = (b − x)(x − a) per a < x < b , e
ψ0 = 0 altrove, si discuta qualitativamente l’evoluzione temporale della funzione d’onda.
1. EQUAZIONE DI SCHRÖDINGER IN UNA DIMENSIONE. PROBLEMI.
5
1.15) Una pallina di massa µ soggetta solo al proprio
peso rimbalza sul pavimento in modo perfettamente
elastico.
V (z) = g µ z .
Trascurando le oscillazioni sul piano xy ,
calcolare l’energia dello stato fondamentale quantistico.
0
1.16) Si valuti la probabilità |τ (k)|2 di
trasmissione di una barriera di potenziale
definita da:
(
λ(x2 − a2 )2 |x| ≤ a
V =
0
a ≤ |x| ,
nell’approssimazione di Born, cioè per |λ|
sufficientemente piccolo.
Si discuta quale sia la scala di riferimento
per λ, cioè cosa significa “λ piccolo”.
−a
0
a
1.17) Una particella si muove in una dimensione
sotto l’azione del potenziale:

+∞



V
1
V =

0



+∞
x≤0
0<x<a
a<x<b
b≤x,
V
1
0
a
b
con a, b, V1 costanti positive. Si trovi
l’equazione che determina lo spettro di energia.
Assumendo che la funzione d’onda iniziale sia: ψ0 (x) = (b − x)(x − a) per a < x < b e
ψ0 = 0 altrove, si discuta qualitativamente l’evoluzione temporale della funzione d’onda.
Se la particella si trova nello stato fondamentale, e si conosce l’espressione esatta del suo
autovalore, si trovi una formula per la probabilità di trovarla nell’intervallo 0 < x < a .
6
1. EQUAZIONE DI SCHRÖDINGER IN UNA DIMENSIONE. PROBLEMI.
1.18) Per un certo sistema, l’Equazione di Schrödinger
in una dimensione ha la forma:
(−
d2
− 2 sech2 x) ψ = W ψ ,
dx2
~ = 1, µ =
0
1
.
2
- Provare che: ψ = exp[ikx] (tanh x + c) è soluzione per
un particolare valore della costante.
- Utilizzare questa soluzione per calcolare i coefficienti
di riflessione e trasmissione e la matrice S per questo problema.
- Anche la funzione d’onda ψ = sech x soddisfa tale equazione. Calcolare l’energia del
corrispondente stato legato, e dare a semplice argomento per ipotizzare che questo sia lo
stato fondamentale.
- Come si poteva procedere per valutare l’energia dello stato fondamentale nel caso non si
conoscesse l’autofunzione?
1.19) Calcolare livelli energetici ed autofunzioni di
una particella di massa µ in moto nel potenziale
V (x) = V0 (a/x − x/a)2 . Che legame esiste
tra lo spettro di questo sistema e quello di un
oscillatore armonico bidimensionale isotropo?
−a 0 a
1.20) Sia data una particella monodimensionale
immersa in un potenziale di Morse:
V (x) = V0 { exp(−2x/a) − 2 exp(−x/a) } .
Determinare autovalori e autofunzioni. Introdurre
p
la nuova variabile y = 2 2µa2 V0 /~ exp(−x/a) ,
e isolare i comportamenti asintotici, operando la
sostituzione: ψ = exp(−y/2) y β φ(y) , con
p
β = −2µa2 W /~ , e W l’autovalore.
1.21) Un fascio di particelle di massa µ
ed energia W è immerso in un potenziale a
gradino di altezza V0 < W , e proviene da sinistra.
a) Valutare la frazione di particelle riflessa.
b) Mostrare che la somma dei flussi delle particelle
riflesse e trasmesse è uguale al flusso delle
particelle incidenti.
W
V
0
0
1. EQUAZIONE DI SCHRÖDINGER IN UNA DIMENSIONE. PROBLEMI.
1.22) Determinare i coefficienti di trasmissione e
riflessione per un potenziale della forma:
V (x) = V0 /[1 + exp(−x/a)] , V0 > 0 , a > 0 .
[Operare le sostituzioni di variabile e funzione:
ψ(z) = z −ik1 a w(z) , z = − exp[−x/a] ,
p
k1 = 2µ(W − V0 )/~2 .]
1.23) Una particella si muove in una dimensione


∞
V (x) = 0

V > 0
0
7
V0
x
0
soggetta al potenziale:
x<0
0≤x≤a
x>a.
a) Data l’equazione trascendente cui deve soddisfare l’energia degli stati legati (vedi 1.2)),
discutere i valori possibili dell’energia, e determinare le autofunzioni normalizzate.
b) Per una particella proveniente da destra con energia W > V0 , determinare lo sfasamento
tra l’onda entrante da destra e quella uscente.
1.24) Determinare il coefficiente di trasmissione
attraverso la barriera:
(
0 x<0, x>a
V (x) =
V0 0 < x < a .
In particolare, discutere i casi:
i) W V0 ; ii) (V0 − W ) µa2 /~2 1 .
iii) W → 0 , ovvero W µa2 V02 /~2 e W V0 .
iv) µa2 V02 /~2 1 e µa2 W 2 /~2 1 .
V0
W
0
a
1.25) Data una buca quadrata, con V = 0 per |x| > b e V = −V0 per |x| < b ,
valutare interamente, a meno della normalizzazione, la funzione d’onda pari dello spettro
continuo. Mostrare che all’interno della buca le frequenze di oscillazione sono maggiori,
mentre i valori massimi sono inferiori.
CAPITOLO 2
Equazione di Schrödinger in due e tre dimensioni. Problemi.
2.1) Sia data la buca sferica, ovvero una particella
tridimensionale soggetta al potenziale:
(
−V0 0 ≤ r < a
V =
0
a<r.
Scrivere l’equazione trascendente che determina
gli autovalori dell’energia, in particolare per
l = 0 e per l = 1 . In questi due casi, individuare
le condizioni che determinano l’esistenza di n
stati legati.
2.2) Una particella bidimensionale si muove libera entro un cerchio, soggetta cioè a un potenziale
bidimensionale a uguale a zero per ρ < a e infinito altrove. Il laplaciano in coordinate polari è
dato da:
1 ∂
∂
1 ∂2
2
∇ =
ρ
+ 2 2 .
ρ ∂ρ ∂ρ
ρ ∂φ
r
0
a
−V0
a
i) Ricavare l’equazione per la funzione radiale
p
R(r) con r = 2µW/~2 ρ .
P
k
ii) Nel caso di autovalore zero per l’operatore angolare, mostrare che R = ∞
k=0 ck r
con ck = 0 se k è dispari e ck+2 = −ck /(k + 2)2 se k è pari.
iii) Dato che il primo zero della funzione R(r) si trova a r = 2.405 , trovare una espressione
per l’energia dello stato fondamentale del sistema.
2.3) Si consideri un atomo di idrogeno in due dimensioni immerso in un campo magnetico trasversale B. Adottando coordinate polari nel piano (r, φ) con momenti coniugati
(pr , pφ ) , determinare i livelli energetici con il metodo di Bohr-Sommerfeld nel limite di
campo debole, trascurando cioè il termine quadratico in B .
9
10
2. EQUAZIONE DI SCHRÖDINGER IN DUE E TRE DIMENSIONI. PROBLEMI.
2.4) Una particella di massa µ può ruotare in un
piano attorno a un punto fisso, collegata a questo
tramite un’asta senza massa di lunghezza λ .
Valutare autovalori e autofunzioni del sistema.
•
2.5) Trovare i livelli energetici dello stato s di una
particella tridimensionale nel campo:
r
V (r) = −V0 e
−r/a
.
Valutare la condizione di esistenza di almeno uno stato
legato. Valutare il numero di altri stati legati in onda
s in funzione di V0 . In particolare, per V0 1 .
[ Suggerimento: operare il cambio di variabile
ρ = λ e−r/2a , con un λ opportuno.]
0
−V0
2.6) Una particella di massa µ e carica elettrica
−e è soggetta a un potenziale
V =
(
0
+∞
ρa <
p
x2 + y 2 < ρ b
B
altrove .
ρa
Solo nel cilindro più interno agisce un campo
ρb
magnetico uniforme e costante nel tempo di
intensità B e direzione ẑ . Scrivere l’equazione di
Schrödinger in coordinate cilindriche e separare le variabili. Dimostrare che esiste un valore
B̄ tale che per B = nB̄ , n = 1, 2, ..., il campo B non altera lo spettro della particella.
(Vedi Olariu S. e Popescu I.I.: Rev. Mod. Phys. 57, 339(1985).)
2.7) Calcolare lo spettro di energia
di un atomo di idrogeno perturbato con
una interazione V = βr −2 , con
β costante positiva.
0
2. EQUAZIONE DI SCHRÖDINGER IN DUE E TRE DIMENSIONI. PROBLEMI.
11
2.8) Una particella di massa µ = 10−24 gr in una buca a simmetria sferica di profondità
−V0 e raggio a = 1.29 10−13 cm , si trova in uno stato legato di momento angolare l = 0
ed energia W = −1.M ev . Calcolare V0 e dire se lo stato legato è l’unico all’interno della
buca. (Sviluppare in serie al primo ordine le funzioni circolari.)
√
2.9) Una particella è descritta dalla Hamiltoniana H = λ p · p + 1/2 K q · q con
λ, K costanti positive. Discutere la dinamica del sistema secondo la meccanica classica.
Impostare il problema in meccanica quantistica, e valutare esplicitamente lo stato fondamentale, sia esattamente che applicando una conveniente approssimazione all’equazione
iterata. (Nel primo caso, quantizzare {qk , pk } nel modo opposto all’usuale.)
2.10) Determinare i livelli energetici discreti di una particella bidimensionale nel potenziale
centrale V (ρ) = −α/ρ . Determinare la loro degenerazione e confrontarla con quella del
caso Coulombiano.
2.11) Data una particella tridimensionale nella buca sferica:
(
−V0 0 < r < a
V (x) =
0
a<r.
determinare qualitativamente le condizioni sufficienti sotto le quali non esistono stati legati
di momento angolare l .
2.12) Determinare autovalori e autofunzioni di una
particella tridimensionale di massa µ immersa nel
pozzo sferico:
(
0
0<r<a
V (x) =
∞ a<r.
Calcolare il valore numerico approssimato per i due
autovalori più bassi nel caso di a = 10−8 cm .
2.13) Un elettrone è confinato in una regione cilindrica di lunghezza c e raggio di base ρb . Il
campo elettrico interno al cilindro è nullo; è presente invece un campo magnetico di cui si conosce
il potenziale:
A= −
F x
F y
, 2
, 0 ,
2
2
+y
x +y
x2
0
r
A
c
ρb
12
2. EQUAZIONE DI SCHRÖDINGER IN DUE E TRE DIMENSIONI. PROBLEMI.
dove F è una costante. Determinare le dimensioni fisiche di F . Scrivere l’Hamiltoniana
dell’elettrone e discutere la natura dello spettro.
2.14) Una particella di massa µ e carica e si trova immersa in un campo elettromagnetico
i cui potenziali vettore e scalare sono espressi in coordinate cartesiane da:
1 2 2
β2
ax − by ay + bx
2
2
,
,
0
V
(x,
y,
z)
=
µω
(x
+
y
+
z
)
+
.
A=
x2 + y 2 x2 + y 2
2
x2 + y 2
Si determini la Lagrangiana e la Hamiltoniana della particella secondo la meccanica classica. Si cerchi la forma più conveniente di entrambe le funzioni attraverso un’appropriata
trasformazione di gauge. Valutare lo spettro di energia sulla base della quantizzazione alla
Bohr-Sommerfeld, e dell’Equazione di Schrödinger.
2.15) Una particella di massa µ si muove su un piano sotto l’azione di una forza avente
energia potenziale (con V0 , a costanti reali positive):


0
V (r, ϕ) = V0 /r 2

∞
0 < r < a , |ϕ| < π/2
0 < r < a, π/2 < |ϕ| ≤ π
a<r
Discutere lo spettro dell’energia con
l’equazione di Schrödinger, oppure
con la quantizzazione di Bohr.
V0
φ
−π
−π/2
0
π/2
a
r
π
0
2.16) Determinare gli stati stazionari di una
particella bidimensionale immersa in un pozzo
circolare (vedi fig. 2.2). Valutare esplicitamente
i primi due autovalori dell’energia.
V (x) =
(
0
∞
0<ρ<a
a<ρ .
2.17) Un atomo di idrogeno è sottoposto a una perturbazione dovuta a un campo magnetico
statico avente potenziale vettore:
p
y
1
x
A = B r02 − 2 , 2 , 0
,
r = x2 + y 2 + z 2 ,
2
r
r
essendo B è una costante che caratterizza l’intensità del campo magnetico e r 0 il raggio
di Bohr. Trascurando i termini in B 2 , valutare autovalori e autofunzioni.
2. EQUAZIONE DI SCHRÖDINGER IN DUE E TRE DIMENSIONI. PROBLEMI.
13
2.18) Un elettrone si muove al di sopra di un conduttore infinito impenetrabile. Esso è
attratto dalla sua carica immagine, per cui classicamente rimbalza elasticamente sul piano.
Scrivere l’equazione di Schrödinger per l’elettrone e valutarne autovalori e autofunzioni,
trascurando gli effetti inerziali della carica immagine.
y
y
e (x,y,z)
z 0
x
x
e (x,−y,z)
2.19) Trovare autovalori e autofunzioni di una particella carica senza spin, immersa in un
campo magnetico uniforme B .
2.20) Una particella di massa µ si muove libera tra due sfere rigide concentriche di
raggi r = a e r = b . Trovare autovalore e autovettore normalizzati relativi allo stato
fondamentale.
2.21) Si consideri una particella carica vincolata a muoversi senza attrito su di una sfera
di raggio R e immersa in un campo magnetico uniforme e costante B. Si determini l’espressione dell’energia in funzione delle variabili di azione Jϑ e Jϕ e quindi si trovi lo
spettro di energia della particella secondo le regole di quantizzazione di Bohr-Sommerfeld.
Si trascurino termini quadratici nel campo B. Quale è il valore caratteristico del campo
per cui l’approssimazione si può considerare valida?
2.22) Si consideri l’Hamiltoniana dell’atomo di idrogeno cui si è aggiunta un potenziale
inversamente proporzionale a sin2 ϑ :
e2
~2 β 2
p2
− +
.
2µe
r
2µe r 2 sin2 ϑ
Si determini lo spettro dell’energia in approssimazione semiclassica, e mediante l’Equazione
di Schrödinger.
H=
2.23) Nel modello di Yukawa due nucleoni di massa M = 940 M ev/c2 si attraggono tramite
lo scambio di un mesone virtuale di massa mπ = 140 M ev/c2 , simulato dal potenziale
non relativistico:
~
g2
.
V (r) = − e−r/d con d =
d
mπ c
14
2. EQUAZIONE DI SCHRÖDINGER IN DUE E TRE DIMENSIONI. PROBLEMI.
Mediante il cambio di variabile x = α e−βr e una scelta opportuna dei parametri α e
β , mostrare che l’equazione radiale di Schrödinger con l = 0 si riduce a una equazione
di Bessel. Supponendo che questo sistema abbia un solo stato legato di energia 2.2 M ev ,
determinare graficamente g 2 /~c tramite le curve accluse delle 11 funzioni di Bessel Jν (x)
per ν = 0, 0.1, 0.2, ..., 0.9, 1 . Quale deve essere il valore minimo di g 2 /~c per avere due
stati legati a l = 0 ? Utilizzare il grafico seguente.
Jν(x)
ν=0
ν=1
x
0
|
|
|
|
|
|
|
|
|
|
|
0 1 2 3 4 5 6 7 8 9 10 11
2.24) Una particella è confinata in una scatola rigida di lunghezza a . i) Scrivere l’autofunzione corrispondente allo stato di minima energia. ii) Dare un valore approssimato del
numero N di stati aventi energia minore di un valore W fissato, nell’ipotesi di N 1 .
[ Sfruttare un’analogia geometrica. ]
2.25) Trovare le condizioni di esistenza di almeno
uno stato legato per una particella tridimensionale
soggetta al potenziale:
(
∞
r<a
V (r) =
−λ/r n r ≥ a , n > 2 .
Si tratta di un potenziale realistico, con una
parte attrattiva a corto raggio al di fuori di
un core repulsivo rigido. [Operare le sostituzioni:
p
y(r) = rR(r) , ν = 1/(n−2) , β = 2ν 2µλ/~2 ,
ρ = β r −1/2ν , y(ρ) = ρ−ν w(ρ) .]
0 a
−λ/r3
2. EQUAZIONE DI SCHRÖDINGER IN DUE E TRE DIMENSIONI. PROBLEMI.
15
2.26) Un oscillatore bidimensionale isotropo si trova nello stato ψ11 (x, y) relativo all’autovalore dell’energia W2 = 3 ~ω . Trovare i possibili valori di una misura del momento
c = −i~ ∂/∂ϕ , e relative probabilità . (Cfr. 2.4)).
angolare M
16
2. EQUAZIONE DI SCHRÖDINGER IN DUE E TRE DIMENSIONI. PROBLEMI.
CAPITOLO 3
Oscillatore Armonico. Problemi.
3.1) Data l’Hamiltoniana dell’oscillatore lineare armonico, l’operatore â :
r
i
µω
1 2
2 2 2
(p̂ + µ ω x̂ )
â =
x̂ + √
H=
p̂ ,
2µ
2~
2µω~
b = â† â .
e il suo aggiunto â† , l’Hamiltoniana si può riscrivere H = ~ ω (N̂ + 1/2) , con N
b e H
b per i quali
Indichiamo con | n i (n = 0, 1, 2, ...) gli autostati ortonormali di N
b |ni=n|ni , H
b | n i = ~ω (n + 1/2) | n i .
N
i) Verificare la regola di commutazione [â, â† ] = 1.
ii) Verificare che â e â† sono degli operatori di distruzione e di creazione con
√
√
â | n i = n | n − 1 i e â† | n i = n + 1 |n + 1 i .
iii) Verificare che lo stato (detto stato coerente)
∞
1 2 X αn
√ | n i,
| α i = exp[− |α| ]
2
n!
n=0
con α costante complessa, è normalizzato ed è autostato di â con autovalore α.
iv) Calcolare h α | β i, osservando che i due autostati non sono ortogonali.
v) Sullo stato | α i calcolare il valore di aspettazione dell’energia e gli scarti quadratici
medi ∆x e ∆p di posizione e momento, verificando che lo stato | α i è a indeterminazione
minima.
vi) Mostrare che, nella rappresentazione delle x , lo stato α è una gaussiana.
3.2) Determinare i livelli energetici dell’Hamiltoniana:
H = ~ω (â†1 â1 + â†2 â2 ) + λ (â†1 â2 + â†2 â1 ) .
Cosa si deve imporre a λ affinchè H abbia solo autovalori positivi.
3.3) Due oscillatori armonici monodimensionali di massa µ = 1 e frequenza ω1 e ω2
sono accoppiati tramite il potenziale V = gx1 x2 . Calcolare lo spettro del sistema.
3.4) Sia data una particella monodimensionale di carica e e massa µ soggetta a un
potenziale V (x) = 1/2 Kx2 e a un campo elettrico E diretto nel verso positivo x.
Determinare autovalori e autovettori dell’Hamiltoniana e i valori medi hxin , hx2 in , hpin , hp2 in ,
valutati sugli autovettori.
17
18
3. OSCILLATORE ARMONICO. PROBLEMI.
3.5) A un oscillatore armonico monodimensionale è sovrapposto un potenziale continuo, lineare
nell’intervallo (−a, a) e costante altrove:
H = p2 /2µ + k/2 x2 + V (x)


−F a x < −a
V (x) = F x
|x| < a

F a
x>a
_
|
F costante .
Fa
0
−a
_
|
a
−Fa
Si valuti la variazione degli autovalori dell’energia rispetto allo spettro dell’oscillatore puro,
prendendo in esame eventualmente qualche caso limite dei parametri a e F .
3.6) Risolvere l’oscillatore armonico tridimensionale isotropo in coordinate cartesiane, cilindriche e sferiche, controllando che le degenerazioni coincidano.
3.7) Un oscillatore armonico bidimensionale isotropo è soggetto a una perturbazione rappresentata dall’operatore: V = λ (â†1 â2 + â†2 â1 ) . Se lo stato del sistema al tempo t = 0 è
dato da | 1, 0 i , calcolare lo stato al tempo t > 0 . (Si intende con | m, n i la base degli
autostati dell’Hamiltoniana imperturbata.)
3.8) Trovare i primi autovalori dell’operatore:
∗ † 2
H = â†1 â1 + 2 â†2 â2 + λ â†2
1 â2 + λ â2 â1
3.9) Si discuta il problema agli autovalori per l’Hamiltoniana:
†2 2
2
H = â†1 â1 + â†2 â2 + λ â†2
â
+
â
â
.
1 2
2 1
3.10) Si determini lo spettro dell’Hamiltoniana:
H = â†1 â1 + â†2 â2 + â†3 â3 + λ Â + Â†
,
Â = â†1 â2 + â†2 â3 + â†3 â1 ,
con â1 , â2 , â3 commutanti tra loro. Si può utilizzare la teoria delle perturbazioni
(degeneri), che però fornisce la soluzione esatta, ottenibile da nuovi operatori diagonali.
3.11) Una particella tridimensionale di massa µ e carica elettrica e è soggetta a un
potenziale di oscillatore armonico isotropo, V = 1/2 k r 2 . Quali sono i livelli energetici e
le loro degenerazioni? Vedi il 3.6 . Se si applica un campo elettrico uniforme, quali sono
i nuovi livelli energetici e quali le loro degenerazioni? Se si applica un campo magnetico
uniforme, quali sono i nuovi livelli energetici e quali le loro degenerazioni? In questo caso,
non trascurare il termine quadratico e utilizzare coordinate cilindriche. Vedi il 2.6 .
3. OSCILLATORE ARMONICO. PROBLEMI.
19
3.12) Trovare gli autovalori dell’energia di una particella di massa µ soggetta al potenziale:
V = A x2 + y 2 + 2αxy + B z 2 + 2βz
A, B > 0 |α| < 1
β qualsiasi .
√
√
Passare alle nuove variabili: ξ = (x + y)/ 2 , η = (x − y)/ 2 , z = z .
3.13) Una particella monodimensionale di massa µ è soggetta a un potenziale V (x) , e si
trova in un autostato dell’energia
1/4
W = ~2 β 2 /2µ .
ψ(x) = β 2 /π
exp [− 12 β 2 x2 ]
Valutare le seguenti quantità: a) il valor medio della posizione, b) il valor medio del momento, c) il potenziale V (x) , d) la probabilità P (p)dp che il momento della particella
sia compreso tra p e p + dp .
3.14) L’Hamiltoniana di un oscillatore armonico in unità adimensionali (µ = ~ = ω = 1) è
p
p
b = â† â + 1/2 con â† = 1/2 (x̂ − ip̂) , â = 1/2 (x̂ + ip̂) . Controllare
il seguente: H
esplicitamente che la funzione ψ = (2x3 − 3x) exp[−x2 /2] , è una sua autofunzione non
normalizzata, valutandone contemporaneamente l’autovalore relativo. Tramite gli operatori
di creazione e distruzione, trovare l’espressione esplicita dei due autostati, non normalizzati,
con gli autovalori più vicini a quello appena calcolato.
3.15) Una particella monodimensionale di massa µ è immersa in un potenziale armonico
V = 1/2 µω 2 x2 . Scrivere la più generale soluzione dell’equazione di Schrödinger dipendente
dal tempo ψ(x, t) , in termini degli autostati dell’oscillatore armonico φn (x) .
Usando l’espressione precedente, mostrare che il valore di aspettazione h x i di x , come
funzione del tempo, può essere scritto come A+ cos ωt + A− sin ωt , con A± costanti.
p
p
p
[Utilizzare la relazione
µω/~ x φn = (n + 1)/2 φn+1 + n/2 φn−1 ]
20
3. OSCILLATORE ARMONICO. PROBLEMI.
CAPITOLO 4
Delta di Dirac. Problemi.
4.1) Discutere lo spettro di una particella in una “buca
quadrata” di semiampiezza b e profondità V0 nel
limite in cui V0 → ∞ , b → 0 con V0 b = λ/2 fissato.
Ricavare anche le condizioni al contorno cui soddisfa la
funzione d’onda nel solo limite b → 0.
−b
b
−V0
4.2) Dato il potenziale V (x) = −λδ(x), integrare l’equazione
di Schrödinger ottenendo le condizioni cui deve soddisfare la
funzione d’onda in x = 0.
a) Dimostrare che queste condizioni definiscono una derivata
seconda autoaggiunta. b) Trovare lo spettro applicando le
condizioni di raccordo ottenute. c) Ritrovare lo stesso
risultato operando la trasformata di Fourier dell’equazione,
e quindi la antitrasformata.
4.3) Si consideri una particella di massa µ in una dimensione
soggetta al potenziale
−x
o
0
x
o
V (x) = −λ+ δ(x − xo ) − λ− δ(x + xo ) ,
con λ+ , λ− , xo costanti positive assegnate.
Determinare gli stati legati della particella e in particolare
valutare la differenza tra i primi due livelli energetici nel
limite xo → ∞ nel caso λ+ 6= λ− e nel caso λ+ = λ− .
4.4) Considerare un oscillatore armonico monodimensionale cui è sovrapposto un potenziale
costante nell’intervallo (−d, d) e zero altrove:
H=
p2
µω 2 2
+
x + Kθ( |x| < d ) .
2µ
2
Si discuta lo spettro dell’energia nei due limiti:
i) d → +∞ , K qualunque;
21
22
4. DELTA DI DIRAC. PROBLEMI.
ii) d → 0 con Kd = λ/2 fissato (perturbazione ∝ δ(x) ).
Nel primo caso si dica rispetto a quale scala di lunghezze si deve intendere il limite.
K
K
−d
0
d
Nel secondo caso, con opportune sostituzioni ci si riduce all’equazione
ψ 00 + ε − ξ 2 − βδ(ξ) ψ = 0 .
Per le soluzioni del potenziale quadratico, vedere il problema 1.9). Per applicare le condizioni di discontinuità della derivata, confrontare A-S 13.4.21 e A-S 13.5.10.
4.5) Determinare i coefficienti di trasmissione e
di riflessione per una particella monodimensionale
soggetta al potenziale V (x) = λ δ(x).
Studiare il caso limite W → ∞ e W → 0 .
4.6) Discutere il problema agli autovalori, per una particella
di massa µ in un grado di libertà soggetta al potenziale
(
λ δ(x) |x| < a
V =
+∞
|x| ≥ a ,
dove δ(x) è la distribuzione di Dirac, e a, λ sono
costanti positive. Discutere inoltre il limite λ → ∞ .
−a
a
4.7) Dato il potenziale:
V (x) = λ[δ(x) + δ(x − a)]
λ > 0,
determinare per quale valore dell’energia
le particelle non si riflettono sulla barriera.
0
a
4. DELTA DI DIRAC. PROBLEMI.
23
4.8) Discutere l’eventuale effetto tunnel da una parte all’altra dell’origine per il potenziale:
(
λ δ(x)
V =
+∞
|x| < a
|x| ≥ a
vedi fig. 4 .6).
4.9) Una particella tridimensionale di massa µ
interagisce con un potenziale centrale:
V (r) = −λ δ(r − a) con a , λ > 0 .
Trovare il minimo di λ per cui esiste uno
stato legato.
a
r
0
4.10) Determinare i livelli energetici di una particella tridimensionale soggetta al potenziale:
V (r) = −λ δ(r − a) . Trovare la condizione di esistenza di stati legati di momento l .
[ Utilizzare il wronskiano Km (x)Im0 (x) − Km0 (x)Im (x) = 1/x ].
4.11) Sia data l’equazione di Schrödinger per
una particella di massa µ soggetta al potenziale:
V (x) = λ/2 [δ(x − a) − 2δ(x) + δ(x + a)] ,
0
−a
a
con λ > 0 .
Determinare lo spettro dell’energia e le
ampiezze di riflessione e trasmissione.
4.12) Una particella monodimensionale di massa µ si
muove nel potenziale periodico:
V (x) =
P∞
n=−∞
λ δ(x − na).
Trovare la diseguaglianza trascendente cui
soddisfa lo spettro a bande.
Nel caso µλa/~2 = 1, risolvere
graficamente lo spettro, indicando in modo
approssimato il primo autovalore dell’energia.
−3a −2a −a 0
a
2a 3a
24
4. DELTA DI DIRAC. PROBLEMI.
4.13) Discutere il problema agli autovalori, inclusa la
loro esistenza, per una particella di massa µ in un
grado di libertà soggetta al potenziale
(
∞,
x<0
V =
−λδ(x − a), 0 < x ,
a
0
dove δ(x) è la distribuzione di Dirac, e a, λ sono
costanti positive.
4.14) Una particella monodimensionale di massa µ è soggetta al potenziale V = −λ δ(x)
con 0 < λ (vedi fig. 4.2) ), e si trova in uno stato legato. Trovare il valore di x0 tale che
la probabilità di trovare la particella in |x| < x0 sia uguale a 1/2 .
4.15) Una particella monodimensionale di massa µ è
immersa nel potenziale
(
∞
x < −a
V =
λ δ(x) −a < x ,
con a, λ > 0 costanti, e al tempo t = 0 si
trova completamente confinata nella regione
−a
0
−a < x < 0 , con una funzione d’onda
uguale all’autofunzione della buca infinita a energia minima. Determinare le autofunzioni
normalizzate dell’Hamiltoniana, proprie e/o improprie. Determinare i coefficienti dello
sviluppo del vettore iniziale su queste autofunzioni. Esprimere la funzione d’onda al tempo
t > 0 , e descrivere qualitativamente il comportamento della particella a tempi grandi.
4. DELTA DI DIRAC. PROBLEMI.
25
26
4. DELTA DI DIRAC. PROBLEMI.
CAPITOLO 5
Perturbazioni indipendenti dal tempo. Problemi.
5.1) Al primo ordine perturbativo, calcolare
l’energia dei primi tre stati di una buca quadrata
infinita di larghezza a , cui sia stato asportato
[ .
il piccolo triangolo OAB
B
5.2) Sia data l’hamiltoniana di un sistema quantistico:
W 1 0
a
H = 0 W2 b a ∗ b∗ W3 0
a
A
con | a | , | b | | Wi − Wj |, per i 6= j . Calcolare autovalori e autofunzioni al primo
ordine della teoria delle perturbazioni.
5.3) Calcolare esplicitamente la separazione del
livello 2p dell’atomo di idrogeno
dovuto all’accoppiamento spin-orbita
(al primo ordine) e mostrare che in unità
dell’energia imperturbata vale e4 /(2~c)2 .
0
5.4) L’atomo idrogenoide è usualmente trattato
assumendo il nucleo a carica puntiforme.
Nell’ipotesi che la carica nucleare sia invece
⊕
⊗
distribuita su una superficie sferica di raggio
δ r0 (raggio di Bohr), calcolare
la variazione di energia dello stato fondamantale
al primo ordine della teoria delle perturbazioni.
Per l’atomo di idrogeno e per δ = 10−13 cm , valutare il risultato rispetto alle energie
imperturbate. (Ricordarsi che il potenziale creato da una distribuzione superficiale di
cariche è continuo).
27
28
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
5.5) Siano date l’hamiltoniana H e l’osservabile A di un certo sistema.
1 i 0
W −iχ
0
iχ .
A = −i 0 −i
H = iχ −W
0 i 1
0 −iχ −3W i) Valutare gli autovalori di H esattamente e, supposto χ piccolo, con la teoria delle
perturbazioni al secondo ordine. Confrontare i risultati.
ii) Al tempo t = 0 una misura di A fornisce come risultato il valore 1 . Calcolare al
tempo t > 0 la probabilitá di trovare il valore −W in una misura dell’energia.
5.6) Studiare lo spettro dell’Hamiltoniana:
H = â† â + λ ( â†2 â + â† â2 ) + â†2 â2
con
[ â, â† ] = 1
al secondo ordine in teoria delle perturbazioni nel parametro λ . Dimostrare inoltre (con
un calcolo esatto) che nel caso λ = 1 lo stato fondamentale è degenere.
5.7) Valutare le correzioni agli stati 1s e 2p
dell’atomo di idrogeno, supponendo la carica distribuita
uniformemente in un volume di raggio rp ≈ 10−13 cm .
Discutere quale sarebbe l’effetto, se al posto
dell’elettrone ci fosse un muone µ− di massa 210
volte superiore.
•
5.8) Una particella si muove in una dimensione soggetta
al potenziale
(
x
V0 cos π
2a
V =
∞
|x|<a
a<|x| ,
con V0 piccolo. Al primo ordine perturbativo in V0
trovare le correzioni alle energie degli stati legati.
−a
0
a
5.9) Una particella di massa µ può ruotare in un piano attorno a un punto fisso, collegata
a questo tramite un’asta senza massa di lunghezza λ . [Vedi 2.4)]
i) Valutare autovalori e autofunzioni del sistema.
ii) Introdotta una perturbazione V0 cos 2φ , con V0 piccolo, calcolare al primo ordine della
teoria delle perturbazioni le variazioni ai tre livelli inferiori di energia. Valutare al secondo
ordine perturbativo la correzione al livello fondamentale.
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
29
5.10) Le differenze ∆1 e ∆2 tra le energie dei primi due livelli eccitati e l’energia del livello
fondamentale di una molecola di massa µ stanno nel rapporto ∆2 /∆1 = 1.96 . Questo
valore è interpretabile entro il 2% schematizzando il moto vibrazionale della molecola
come quello di un oscillatore armonico semplice.
Si aggiunga al potenziale armonico V = 1/2 K x2 un potenziale “piccolo” V 0 = ax3 +bx4 .
Trattando V 0 al primo ordine perturbativo, si determinino, in funzione di ∆1 e ∆2 , le
costanti k, a , b , in modo da rendere esatto l’accordo con il valore sperimentale.
5.11) Due particelle identiche di massa µ e spin 1/2 si muovono in una scatola cubica
di lato 2l . Calcolare i primi due autovalori dell’energia. Al primo ordine perturbativo
dire se e come viene risolta la degenerazione del secondo livello in presenza del potenziale
V = λ δ3 (x1 − x2 ) , con λ > 0 . [Vedi fig. 4.6). ]
5.12) Per un potenziale di Morse:
V (x) = V0 { exp[−2(x − x0 )/a] − 2 exp[−(x − x0 )/a] }
relativo a una particella di massa µ , si possono studiare le piccole oscillazioni attorno al punto di equilibrio
x0 , riducendo il potenziale a quello di un oscillatore
armonico di opportuna frequenza. Dire se e per quali
stati legati tale approssimazione può essere valida
per un sistema caratterizzato dai seguenti valori:
V0 = 10−2 ev , µ = 10−23 gr , a = 5.10−8 cm . [Cfr. 1.20)]
x
|
0
5.13) L’Hamiltoniana di un sistema sia:
2 − i −
0
−i .
H = 2 + i
−
i
0
Trovare autovalori e autofunzioni del sistema per = 0 e le correzioni da apportare ai
livelli energetici, al primo ordine perturbativo in .
5.14) Si consideri una particella di spin 1/2 sottoposta a un campo magnetico Hx = B ,
Hy = 0 , Hz = A , e si supponga B A .
Calcolare i livelli energetici al primo e secondo ordine della teoria delle perturbazioni.
5.15) Si cosideri una particella su un segmento di lunghezza a con condizioni periodiche
al contorno. Si determinino le autofunzioni dell’energia e i corrispondenti autovalori.
Introdotta la perturbazione V = V0 exp[−λx] , calcolare al primo ordine perturbativo in
V0 le correzioni al primo livello eccitato, nell’ipotesi 1/a λ .
30
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
5.16) Calcolare al primo ordine perturbativo le correzioni ai primi due livelli di energia di
un atomo di idrogeno dovuti al momento di dipolo elettrico del nucleo.
5.17) Sia H0 = p2 /2µ + µ/2 ω 2 q 2 l’Hamiltoniana di un oscillatore armonico a un grado
di libertà. Sia V = â†2 â2 una perturbazione, essendo â l’operatore di annichilazione
√
â = (p − iµωq) / 2µ~ω .
i) Trovare la dipendenza funzionale di un generico livello di energia dell’Hamiltoniano
H = H0 + λV , cioè Wn = Φ(µ, ~, ω, λ) , con semplici considerazioni dimensionali.
ii) Calcolare la correzione al secondo ordine in teoria delle perturbazioni per l’autovalore e
per l’autovettore dello stato fondamentale.
5.18) Calcolare al primo ordine la correzione al livello n = 2 di un atomo di idrogeno
dovuta al potenziale: V = cos θ/r α , con 0 < e 0 < α ≤ 2 . (Vedi il 5.16).)
5.19) Sia data H0 = p2 /2µ + µ/2 ω 2 q 2 , Hamiltoniana di un oscillatore armonico ad un
grado di libertà. Sia inoltre V = λ1 q 3 + λ2 q 4 una perturbazione “piccola”.
Con semplici considerazioni dimensionali, trovare la dipendenza funzionale di un generico
livello di energia dell’Hamiltoniano H = H0 + V , cioè Wn = Φ(µ, ~, ω, λi ) .
Calcolare inoltre, al primo ordine perturbativo, la correzione agli autovalori dell’energia.
5.20) Calcolare la perturbazione al primo ordine dello stato fondamentale dell’atomo di
idrogeno dovuta alla correzione relativistica −p4 /8µ3 c2 .
5.21) L’Hamiltoniana di un sistema quantomeccanico a un grado di libertà è data da
H = p2 /2µ + µ/2 ω 2 q 2 + λq 4 dove {q, p} sono gli operatori canonici, e µ, ω, λ sono
costanti positive.
Dimostrare, attraverso considerazioni dimensionali, che ogni livello discreto di energia è
rappresentabile con l’espressione Wn = ~ω Φn (χ) , dove Φn è un’opportuna funzione
di χ = ~λ /µ2 ω 3 . Assumendo nota la funzione Φn , calcolare i valori di aspettazione
h n | q 2 | n i , h n | p2 | n i , h n | q 4 | n i , essendo | n i l’autostato dell’energia
appartenente a Wn . Determinare Φn (χ) al 20 ordine in teoria delle perturbazioni e
applicare il risultato al calcolo dei valori d’aspettazione ottenuti in precedenza.
5.22) Calcolare perturbativamente lo spettro dell’operatore H = â† â + λ | ψ ih ψ | , con
| ψ i vettore normalizzato e {â† , â} gli ordinari operatori di creazione e distruzione.
P∞
n
Considerare in particolare | ψζ i = N
n=0 (ζ /n!) | n i , con | n i autovettori di
H0 = â† â . Cosa si può dire per λ → ±∞ ?
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
31
5.23) Una particella si muove in una dimensione
soggetta al potenziale
(
x
V0 cos2 π
0<x<a
a
V =
∞
altrove ,
Al primo e al secondo ordine perturbativo in V0
trovare le correzioni alle energie degli stati legati.
Indicare le condizioni di validità del procedimento.
0
a
5.24) Valutare al primo ordine perturbativo le correzioni al secondo stato legato (n=2) dell’atomo di idrogeno, dovute a un campo elettrico e un campo magnetico uniformi, costanti
e parelleli tra di loro.
5.25) Una particella senza spin di massa µ si muove
in un campo centrale della forma:

V0


V (r) = − r/a
e −1
2


α = µa V0 1 .
~2
r
0
Al primo ordine perturbativo in 1/a , calcolare le
correzioni ai livelli energetici del potenziale
coulombiano Ve (r) = −V0 a/r . Notare la risoluzione
della degenerazione accidentale. [Sviluppare il potenziale in serie di r/a , giustificando il procedimento per i valori assegnati dei parametri. Ricordare che (unlm , r unlm ) =
1/2 [ 3n2 − l(l + 1) ] r0 con r0 raggio di Bohr. ]
5.26) Si consideri un oscillatore armonico perturbato in due gradi di libertà:
H0 = p21 /2µ1 + p22 /2µ2 + µ1 /2 ω12 q12 + µ2 /2 ω22 q22 + λ q12 q22
Determinare la correzione all’energia dello stato fondamentale al secondo ordine in λ .
Discutere il calcolo perturbativo dei livelli eccitati.
5.27) Consideriamo un oscillatore armonico isotropo perturbato:
†
†
†
†
†
H = ~ω â1 â1 + â2 â2 + â3 â3 + λ â1 â2 + â2 â1 .
(0)
Calcolare la correzione ai primi tre autovalori imperturbati WN = N ~ω, {N = 0, 1, 2} ,
sia mediante lo sviluppo perturbativo che in forma chiusa mediante un calcolo esatto.
32
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
5.28) Una particella di massa µ e carica −e0 è attirata nell’origine da una forza elastica
di intensità K/2 r . Il sistema è immerso in un campo magnetico uniforme e costante
di modulo B diretto lungo l’asse ẑ . i) Con un opportuno potenziale vettore, scrivere
l’Hamiltoniana del sistema. ii) Se B è molto piccolo, calcolare i primi autovalori dell’energia.
5.29) Un oscillatore armonico isotropo in due gradi
di libertàè soggetto ad una pertur
†2 2
2
bazione rappresentata dall’operatore V = λ â1 â2 + â†2
. Posta uguale a uno la
2 â1
frequenza dell’oscillatore e la costante di Planck ~ , si determini la correzione dei primi
livelli energetici, W ≤ 5 , al primo ordine in teoria delle perturbazioni.
5.30) Sia dato un atomo idrogenoide di carica Z nello stato fondamentale. Valutare i
valori di aspettazione dell’energia cinetica e potenziale. Con la tecnica perturbativa al
primo ordine, valutare la variazione di energia quando la carica del nucleo passa da Z a
Z + 1 , e confrontare con il dato esatto.
5.31) Si consideri un sistema quantistico caratterizzato dall’operatore Hamiltoniano
†2 2
2
H = â†1 â1 + â†2 â2 + λ â†2
â
+
â
â
.
1 2
2 1
Trovare gli autovalori di H che per λ piccolo tendono a W (0) = 0, 1, 2, 3 .
5.32) Considerare il seguente potenziale isotropo
tridimensionale:

1
2 2


a< |x|
 µω x
2
V =


V
|x| <a,
0
Si valuti la correzione ai primi due livelli energetici,
al primo ordine in V0 e nel limite di a molto piccolo
rispetto alla scala di lunghezza tipica dell’oscillatore.
5.33) Una particella tridimensionale di massa
soggetta al potenziale di Yukawa:
V (r) = −γ
e
µ
−a
0
a
è
−r/ρ
r
V0
.
Valutare al primo ordine perturbativo le correzioni ai
livelli energetici dell’atomo di idrogeno. Giustificare
l’approssimazione nel caso che i parametri soddisfino la
relazione µγρ/~2 1 .
r
0
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
33
5.34) Una particella è immersa in una buca di potenziale infinita di larghezza a ( 0 < x < a ).
Al primo ordine perturbativo valutare come si modificano i livelli energetici se si aggiungono
le perturbazioni del tipo:


0<x<b
0
V0
V1 = ( a − | 2x − a | )
V2 = V0 b < x < a − b

a
0
a−b <x<a .
V
V
1
0
2
a
0
b a−b a
5.35) Un rotatore piano di momento di inerzia I e di momento elettrico di dipolo d è
immerso in un campo elettrico omogeneo E giacente nel piano di rotazione. Mediante un
calcolo perturbativo, determinare le correzioni ai livelli energetici dello stato fondamentale,
del primo stato eccitato e di quelli successivi.
5.36) Consideriamo l’Hamiltoniana:
p2
1
+ µω 2 q 2 + λp4 .
2µ 2
Al secondo ordine in λ , valutare le correzioni agli autovalori dell’oscillatore armonico.
H=
5.37) Una particella di massa µ si muove su una circonferenza di raggio r̄ ed è soggetta
al potenziale: V = λ sin ϕ cos ϕ , dove ϕ individua la posizione angolare della particella.
Al secondo ordine della teoria delle perturbazioni, valutare i primi tre livelli energetici.
5.38) Un elettrone è confinato in una scatola cubica di lato a orientata con le facce
parallele agli assi x, y, z , e ha energia pari
a W = 3h2 /4µa2 . Ad un certo istante si
accende un campo elettrico E costante e
uniforme, parallelo all’asse z. i) Calcolare al
primo ordine perturbativo come si modifica
l’autovalore dell’energia. ii) Ripetere il
calcolo con la perturbazione H 0 = eExy .
34
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
5.39) Un atomo di idrogeno è sottoposto a una perturbazione dovuta a un campo magnetico
statico avente potenziale vettore:
y
p
1
x
A = Br02 − 2 , 2 , 0
, r = x2 + y 2 + z 2 ,
2
r
r
essendo B è una costante che caratterizza l’intensità del campo magnetico e r 0 il raggio
di Bohr. Determinare le correzioni perturbative ai livelli energetici al primo ordine in B ,
e discutere la validità dell’approssimazione. Confrontare il risultato con lo sviluppo in serie
dei valori esatti trovati nel 2.17) .
5.40) Risolto esattamente l’esercizio precedente al primo ordine in B , valutare al primo
ordine perturbativo le correzioni dovute al termine in B 2 .
5.41) Sia dato il potenziale
1
2
2
2
V (x, y, z) = K x + y + z + λxy ,
2
e una particella massiva immersa in esso. Nell’ipotesi di λ piccolo, valutare: i) al secondo
ordine in λ le correzioni all’energia dello stato fondamentale; ii) al primo ordine in λ le
correzioni all’energia del primo stato eccitato.
5.42) Con ~ω = 1 , sia H0 = â† â l’Hamiltoniana di un oscillatore armonico traslato.
Trovare lo spettro dell’operatore: H = H0 + λ (â†2 â + â† â2 ) in teoria delle perturbazioni
all’ordine λ3 . [Poichè l’operatore di parità Pb soddisfa alle relazioni Pb H0 = H0 Pb e
Pb â = −â Pb , si dimostra che gli autovalori di H dipendono solo da λ2 , e quindi...]
5.43) Una distribuzione continua di carica elettrica genera un campo centrale E che
corrisponde a un potenziale: V (x) = 21 K x2 . i) Scrivere l’Hamiltoniana quantistica per
una particella di carica e e spin ~/2 , tenendo conto anche della interazione spin-orbita.
ii) Determinare lo spettro di energia. iii) Se la carica è distribuita su un volume finito (una
sfera di raggio R), come si modifica lo spettro?
5.44) Un atomo di idrogeno è sottoposto all’azione del campo esterno E di componenti
xz yz
x2 + y 2
,
,
−
},
r3 r3
r3
con α costante positiva. Determinare se esiste un potenziale V tale che E = ∇ V ,
e individuare le costanti del moto in presenza del campo esterno. Determinare al secondo
ordine in α la correzione allo stato fondamentale e al primo ordine quella per il primo
livello eccitato, esprimendo formalmente il risultato in termini degli integrali:
Z ∞
Z ∞
dr unl un l+1 ,
dr unl u10 e dn,l =
cn,l =
E=α{
0
0
dove Rnl = unl /r è la parte radiale delle autofunzioni dell’atomo d’idrogeno.
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
35
[Si faccia uso della formula soddisfatta dalle armoniche sferiche:
p
cos ϑ Ylm (ϑ, ϕ) = (l + 1 − m)(l + 1 + m)/[(2l + 1)(2l + 3)] Yl+1,m +
p
+ (l − m)(l + m)/[(2l − 1)(2l + 1)] Yl−1,m . ]
5.45) Una particella di massa µ si muove in un potenziale di oscillatore armonico isotropo
perturbato:
1
κ2 2 2 2
V = µω 2 x2 + y 2 + z 2 + κ xyz +
x y z ,
2
~ω
con κ costante, il medesimo in entrambi i termini. Calcolare le correzioni all’energia dello
stato fondamentale al secondo ordine in κ .
5.46) Si consideri l’Hamiltoniana
p
1
p2
+ µω 2 q 2 + V0 cos ( µω 0 /~ q)
H=
2µ 2
dove p e q sono gli operatori canonici, µ, ω, ω 0 e V0 sono costanti positive. Si studi
lo spettro di energia nel limite V0 ~ω utilizzando la teoria delle perturbazioni. Si
discutano anche i limiti ω 0 → ∞ e ω 0 → 0 .
5.47) Sia dato l’Hamiltoniana:
p2
+ K ( 1 − cos (αq) ) ,
H=
2µ
con µ, K, α costanti positive. Si discutano le condizioni sui parametri affinchè sia possibile
considerare corretta l’approssimazione quadratica 1 − cos (αq) ≈ 1/2 α 2 q 2 .
5.48) Si determini lo spettro dell’Hamiltoniana
p2
1
+ µω 2 q 2 + F q + Gq 2
2µ 2
in teoria delle perturbazioni, considerando F e G costanti “piccole” con F 2 ≈ ~ωG .
H=
5.49) Si determini lo spettro di bassa energia dell’Hamiltoniana:
H = â†1 â1 + â†2 â2 + λ ( â†1 2 â2 + â†2 â21 ) ,
in teoria delle perturbazioni, e limitatamente ai primi quattro livelli.
5.50) Consideriamo l’oscillatore bidimensionale isotropo perturbato:
1
1
1
H = (p2x + p2y ) + (x2 + y 2 ) + λ xy (x2 + y 2 ) .
2
2
2
Al primo ordine perturbativo, valutare le correzioni ai primi due autovalori dell’oscillatore
armonico imperturbato. Dare una stima del valore di λ per cui l’approssimazione è valida.
36
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
5.51) Una particella monodimensionale carica è soggetta a un potenziale di oscillatore
armonico, ed è immersa in un campo elettrico E uniforme e costante. In teoria delle
perturbazioni fino all’ordine E 2 valutare le correzioni alle energie degli stati legati.
5.52) Consideriamo l’Hamiltoniana:
H=−
d2
+ x2 + αx3 .
dx2
Valutare la prima correzione perturbativa diversa da zero allo stato fondamentale dell’oscillatore armonico.
5.53) Una massa µ è collegata a un perno P da una barra
senza massa di lunghezza a .
i) Nella prima approssimazione di piccoli angoli,
trovare i livelli di energia quantistica del sistema.
ii) Trovare la prima correzione allo stato fondamentale
per l’approssimazione successiva.
⊕P
⊗
a
µ
5.54) Un oscillatore armonico monodimensionale è
soggetto a una piccola perturbazione del tipo:
V0 =
θ
•
2
λ/a
λ
.
x2 + a 2
Calcolare la correzione allo stato fondamentale
al primo ordine perturbativo, nel caso che:
p
p
i) a ~/µω , ii) a ~/µω .
5.55) Una particella monodimensionale di carica −e e
massa µ è immersa nel potenziale :

 K
x>0
−
V (x) =
x
∞
x≤0,
0
V′
x
con K costante positiva.
Calcolare l’energia dello stato fondamentale.
Nel caso venisse applicato un piccolo campo elettrico
in direzione x , valutare l’effetto Stark al primo ordine perturbativo.
5.56) Una particella di massa µ può ruotare in un piano attorno a un punto fisso, collegata
a questo tramite un’asta senza massa di lunghezza λ . i) Valutare autovalori e autofunzioni
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
37
del sistema. ii) Introdotto il potenziale V0 cos 2ϕ , calcolare al primo ordine in V0 della
teoria delle perturbazioni le variazioni agli autovalori e alle autofunzioni.
5.57) Consideriamo un atomo di Elio con 2 elettroni a spin zero. i) Trascurando la repulsione
Coulombiana, scrivere lo stato fondamentale dell’energia e il suo autovalore. ii) Con la
teoria delle perturbazioni al primo ordine, valutare la correzione dovuta alla repulsione tra
gli elettroni. ii) Con questo risultato, stimare l’energia di ionizzazione dell’Elio. [ Utilizzare
RR
la relazione:
d3 r1 d3 r2 exp{−a · (r1 + r2 )} / |r1 − r2 | = 20π 2 /a5 .]
5.58) Sia dato un oscillatore harmonico tridimensionale isotropo, di frequenza ω e massa
µ , perturbato da un potenziale V = λxy , con λ costante. Al primo ordine, trovare le
correzioni all’autovalore del primo stato eccitato imperturbato, e i relativi autostati.
5.59) Al primo ordine perturbativo, calcolare le correzioni al primo livello eccitato di un
oscillatore armonico bidimensionale isotropo soggetto alla perturbazione V 0 = λ xy .
Determinare le funzioni corrette all’ordine zero (λ → 0). Confrontare con la soluzione
esatta per λ 6= 0 .
5.60) Al primo ordine perturbativo, calcolare le correzioni all’energia del secondo livello
eccitato di un oscillatore armonico bidimensionale isotropo soggetto alla perturbazione
V 0 = λ xy . Determinare le funzioni corrette all’ordine zero (λ → 0 ). Confrontare con la
soluzione esatta per λ 6= 0 . (Vedi 5.59))
5.61) Una buca infinita in 0 < x < a è soggetta anche a V 0 (x) = λ δ(x − a/2) .
Considerando questo termine come una perturbazione, calcolare i contributi allo spettro al
primo e al secondo ordine. Indicare le condizioni di applicabilità del risultato ottenuto.
[ Sfruttare la relazione: [(2k + 1)2 − (2p + 1)2 ]−1 = [4(2k + 1)]−1 [(p + k + 1)−1 − (p − k)−1 ] .]
5.62) Un atomo mesico di numero atomico Z è costituito da un ordinario atomo nel
quale un mesone µ ha sostituito uno degli elettroni. Inizialmente il muone è catturato
su un’orbita eccitata simile a quella dell’elettrone espulso, per poi scendere rapidamente ai
livelli più bassi per emissione a cascata di raggi X , o di altri elettroni per effetto Auger.
A causa della sua massa elevata, mµ ≈ 206me , il suo raggio di Bohr è molto più piccolo
di quello degli elettroni, ovvero le sue orbite sono molto più vicine al nucleo di quelle di
tutti gli elettroni, e quindi risente in modo accentuato della distribuzione di volume della
carica nucleare, e molto poco della carica elettronica, per lo più esterna all’orbita µ .
Dunque, il potenziale di Coulomb effettivo sul muone interno può essere approssimato da:
V (r) = −Ze2 δ (3/2 − r 2 /2δ 2 ) per r < δ , e V (r) = −Ze2 /r per r > δ . Vedi 5.7).
a) Valutare l’energia dei livelli 1s , 2s e 2p dell’atomo mesico al primo ordine delle
perturbazioni per δ r0µ , dove r0µ è il raggio di Bohr del mesone.
38
5. PERTURBAZIONI INDIPENDENTI DAL TEMPO. PROBLEMI.
(1)
(1)
b) Posto che per Z = 5 si trovi W2s − W2p ≈ 2 · 10−2 eV , ricavare una stima di δ .
Ricordare che le prime funzioni d’onda dell’atomo mesico idrogenoide ( Z = 1 ) sono le
√
3/2
3/2
seguenti: ψ1s = 2 N0 e−ρ̃ Y00 , ψ2s = 1/ 2 N0 (1 − ρ̃/2) e−ρ̃/2 Y00 ,
√
3/2
ψ2p = 1/2 6 N0 ρ̃ e−ρ̃/2 Y1m , dove N0 = 1/r0µ , ρ̃ = r/r0µ , e le Y le armoniche
sferiche.
5.63) Un atomo di idrogeno è perturbato da un campo non centrale V 0 = f (r)xy , con f (r)
non specificata ma ovunque regolare. Al primo ordine perturbativo, valutare le correzioni
del livello con n = 2 e le loro eventuali degenerazioni residue, in funzione di un parametro
incognito legato ai valori di aspettazione della funzione f (r) .
CAPITOLO 6
Calcolo Variazionale. Problemi.
6.1) Volendo utilizzare il principio variazionale di Riesz per la valutazione approssimata
dello stato fondamentale di una buca infinita con 0 ≤ x ≤ a, dire quali dei due polinomi
seguenti può essere utilizzato come funzione di prova e perchè:
ψ1 = x(l − x)
ψ2 = x(l − x)(x − a) ,
essendo l un parametro variazionale.
6.2) Calcolare il valore approssimato dell’energia dello stato fondamentale di un oscillatore
armonico con il metodo variazionale, utilizzando le funzioni di prova:
x2
x2
a) ψ1 (x) = A(1 + 2 )−1
b) ψ2 (x) = B(1 + 2 )−2 ,
a
a
essendo a il parametro variazionale.
Dire per quali valori dei parametri a e b la funzione di prova:
x2 2
ψ(x) = C(1 + 2 )−b
a
riproduce meglio l’andamento della autofunzione esatta dello stato fondamentale, e valutare
l’errore minimo sull’autovalore.
[ Per la prima e per la seconda domanda, rispettivamente, utilizzare le formule:
Z
Z ∞
dx
1 d ∞
x
dx
=−
,
e−x = lim (1 + )−ν .]
2
n+1
2
n
ν→∞
n db −∞ (b + x )
ν
−∞ (b + x )
6.3) Una pallina di massa µ soggetta solo al proprio peso rimbalza sul pavimento in modo
perfettamente elastico. Trascurando le oscillazioni sul piano xy, valutare l’energia dello
stato fondamentale con il metodo variazionale, utilizzando come funzioni di prova:
ψ1 (z) = Aze−αz
ψ2 (z) = Bze−βz
2 /2
.
Confrontare con il valore esatto dell’esercizio 1.15).
6.4) Mediante il metodo variazionale ricavare il valore approssimato dell’energia dello stato
2p di una particella in campo coulombiano, utilizzando le funzioni di prova:
ψ(r) = a · r exp[−α2 r 2 ] ,
con a vettore costante e α parametro variazionale.
Confrontare con il valore esatto e giustificare la scelta delle funzioni di prova.
39
40
6. CALCOLO VARIAZIONALE. PROBLEMI.
6.5) Calcolare il valore approssimato dell’energia dello stato fondamentale di un oscillatore
armonico bidimensionale, utilizzando il metodo variazionale con le funzioni di prova:
p
ψα (ρ) = C exp(−αρ) ,
ρ = x2 + y 2 ,
con α parametro variazionale.
6.6) Con il principio variazionale di Riesz, stimare il primo stato eccitato dell’oscillatore
armonico, usando come funzioni di prova una delle due seguenti: ψ1 (x) = A x e−α|x| ,
ψ2 (x) = A x2 e−α|x| , con α parametro variazionale. Giustificare la scelta.
6.7) Applicare il principio variazionale di Riesz all’oscillatore armonico tridimensionale
isotropo, usando come funzioni di prova:
ψ(r) = a · r exp[−αr] ,
con a vettore costante e α parametro variazionale. Dire di quale autostato questa può
essere ritenuta una buona approssimazione, e calcolare gli autovalori approssimati.
6.8) Sia data l’Hamiltoniana:
H = p2 /2µ + λx2k ,
con k intero positivo. i) Con la semplice analisi dimensionale, dimostrare che per λ → ∞ ,
E0 ≈ λ1/k+1 . ii) Applicando il metodo variazionale con funzioni di prova gaussiane, dare
una stima approssimata dello stato fondamentale, autofunzione e autovalore.
6.9) Un elettrone senza spin si muove nel potenziale a simmetria sferica V = λr , con
λ > 0 . Con il metodo variazionale e una funzione di prova esponenziale, trovare un valore
approssimato per l’energia dello stato fondamentale.
6.10) - Mediante il metodo variazionale ricavare il valore approssimato dell’energia dello
stato fondamentale di una particella immersa in un campo coulombiano, utilizzando come
funzioni di prova:
(
A (α − r) r ≤ α
−α2 r 2
;
ψii (r) =
ψi (r) = A e
0
r≥α,
con α parametro variazionale. -Le funzioni di prova sono entrambe accettabili? -Ignorando
il valore esatto, quale dei due valori rappresenta una migliore approssimazione? -Era questo
prevedibile dalla forma delle funzioni di prova?
6.11) Una particella tridimensionale si muove nel potenziale: V (r) = −λ/r 3/2 .
Per valutare un limite superiore dell’energia dello stato fondamentale, utilizzare il calcolo
variazionale con una funzione idrogenoide quale funzione di prova.
6. CALCOLO VARIAZIONALE. PROBLEMI.
41
6.12) Una particella si trova in una buca infinita nell’intervallo 0 < x < a . Assumere come
approssimazione allo stato fondamentale una delle seguenti funzioni: 1) ψ1 (x) = A x(x−a) ,
2) ψ2 (x) = B sin2 (πx/a) , 3) ψ3 (x) = C (a/2 − |x − a/2|) , e valutare il relativo valore
di aspettazione dell’energia. Confrontare con il valore esatto. Sulla base del principio
variazionale di Riesz, dire se tutte le funzioni di prova rappresentano una scelta opportuna,
e spiegare perchè la prima fornisce un risultato migliore.
6.13) Calcolare il valore approssimato dell’energia dello stato fondamentale di una particella
nel campo V (x) = −λδ(x) , utilizzando a come parametro variazionale nelle funzioni di
prova: 1) ψ1 (x) = A(1 + x2 /a2 )−1
2) ψ2 (x) = B(1 + x2 /a2 )−2 .
Confrontare con il risultato esatto.
6.14) Data una buca infinita per −a < x < a , trovare il polinomio di grado minimo
adatto ad approssimare il primo stato eccitato. Confrontare la corrispondente energia
approssimata con il risultato esatto.
6.15) Sia dato il potenziale del problema 4.13). Mediante il metodo di Riesz, dare una stima
dei parametri del potenziale per i quali è garantita l’esistenza dello stato legato. Utilizzare
le seguenti funzioni di prova, con χ parametro variabile: ψ1 (x) = A x exp(−χx),
ψ2 (x) = B x exp(−χx2 /2) . Confrontare con il valore esatto trovato nel 4.13). (Notare le
√
2
diseguaglianze ey /y ≥ e , ey /y ≥ 2e .)
42
6. CALCOLO VARIAZIONALE. PROBLEMI.
CAPITOLO 7
Evoluzione temporale. Problemi.
7.1) La funzione d’onda a t = 0 per un elettrone libero è data da:
ψ0 (x) = (2πα2 )−1/4 e−x
2 /4α2
con α = 0.53 10−8 cm . Dopo quanto tempo ∆xt = 1cm ? E se fosse µ = 10−3 gr ?
7.2) Sia data l’hamiltoniana e altre tre osservabili di un sistema fisico:
0 1
−1 1
1 0 1 0
.
H = w A = a B = b C = c 1 0
1 1
0 −1
0 0
i) Determinare quali delle osservabili sono costanti del moto. ii) Una misura di C al tempo
t = 0 da per risultato il valore 0 . Quale sarà al tempo t > 0 il risultato di una misura
di A ? iii) Determinare almeno tre differenti sistemi completi di osservabili.
7.3) Siano date le matrici
matrice H relativa alla
sua
0 −i
A = a i 0
0 0
A e B relative
hamiltoniana:
1
0 0 B = b 0
0
−1
a due osservabili per un certo sistema, e la
0 0 1 0 0 −1
0 0 0
H = w 0 0 1 .
0 1 0
i) Verificare che le due grandezze sono compatibili.
ii) Supposto di avere eseguito al tempo t = 0 una misura delle due grandezze e trovato il
valore −a per la prima e b per la seconda, calcolare la funzione d’onda al tempo t > 0 .
7.4) Un pacchetto d’onde associato a particelle neutre
di spin 1/2 e momento magnetico intrinseco µ0 σ ,
attraversa un campo magnetico B = 0, 0, B(z) .
i) Scrivere l’equazione di Schrödinger per la funzione
d’onda:
ψ1 (t)
.
ψ(t) = ψ2 (t)
ψ1
B
ψ2
ii) Per un dato iniziale del tipo ψ0 = χσ φ(x ), con χσ
spinore arbitrario, e per h d/dz B(z) i ≈ d/dhzi B(hzi) , dimostrare che il fascio si separa,
ovvero che ψ1 (t) e ψ2 (t) rappresentano due pacchetti d’onde i cui due baricentri
h x ii,t = h ψi (t) | x | ψi (t) i (i = 1, 2) si muovono su traettorie divergenti.
43
44
7. EVOLUZIONE TEMPORALE. PROBLEMI.
7.5) Un oscillatore lineare armonico di massa µ e frequenza ω è descritto al tempo t = 0
dalla funzione d’onda normalizzata:
r
µω 1/4
√
√
µω
−ξ 2 /2
ψ0 (x) =
.
ξ=x
e
( 2 ξ − 3),
16π~
~
Trovare il valor medio della posizione e dell’energia in funzione del tempo.
7.6) Siano date le matrici A
matrice H relativa alla sua
0 1 0
A = a 1 0 1 B = b
0 1 0
, B e C relative a tre osservabili per un certo sistema, e la
hamiltoniana:
0
2 0 0 1 0
iw1 0 0 0 0 −1 C = c 0 3 0 H = −iw1 0
0 ,
0
0 0 3 0 −1 0 0 w2 con a, b, c > 0 . Osservato al tempo t = 0 il valore massimo di A , calcolare la probabilità
di trovare al tempo t > 0 :
i) il valore massimo di B ; ii) Contemporaneamente i valori massimi di B e C .
7.7) E’ data una particella di spin 1/2 e momento magnetico −µ0 σ , con σ matrici di
Pauli. Al tempo t = 0 una misura della componente dello spin lungo l’asse x dà come
risultato ~/2 . Per t > 0 su di essa agisce il campo magnetico B = 0, 0, B0 (1 − e−t ) .
Trovare i valori medi delle tre componenti dello spin in funzione del tempo e verificare che
questi, nel limite t → ∞ , sono funzioni periodiche del tempo.
7.8) Un elettrone si muove in un campo magnetico uniforme B0 diretto come l’asse z .
Dall’istante t0 = 0 agisce su di esso un altro campo magnetico uniforme B1 diretto
come l’asse x . Supposto lo spin dell’elettrone inizialmente orientato secondo la direzione
positiva dell’asse z , calcolare al tempo t la probabilità di trovare lo spin capovolto.
7.9) Una particella di spin 1 (di cui si considerano solo i gradi di libertà di spin) è immersa
in un campo magnetico statico diretto come l’asse y , ovvero H = τ sy , con s operatore
di spin. Se all’istante t = 0 una misura di sx fornisce come risultato ~ , quale è la
probabilità di ottenere ~ in una misura di sz al tempo t > 0 ?
7.10) Una particella di spin 1/2 e momento magnetico µ0 = 1/2 g~σ si trova immersa
in un campo magnetico oscillante nel tempo e di direzione costante B = (0, 0, B sin(ωt)) .
Se lo stato iniziale della particella è autostato della componente x dello spin, calcolare la
distribuzione di probabilità per tutte le componenti dello spin in funzione del tempo.
7.11) Sia data una particella di spin s = 1/2 e momento magnetico µ , immersa in un
campo magnetico omogeneo stazionario. Determinare l’operatore vettoriale di spin ŝ(t)
in rappresentazione di Heisenberg, con due procedimenti:
7. EVOLUZIONE TEMPORALE. PROBLEMI.
45
i) tramite la trasformazione unitaria che collega gli operatori delle osservabili in rappresentazione di Heisenberg e di Schrödinger, utilizzando il lemma di Baker-Hausdorff:
exp(A)B exp(−A) = B + [A, B] +
1
1
[A, [A, B]] + [A, [A, [A, B]]] + ...) ;
2!
3!
ii) risolvendo le equazioni del moto per gli operatori s± in rappresentazione di Heisenberg.
7.12) Studiare il moto di un pacchetto d’onde
gaussiano che evolve secondo l’equazione di
Schrödinger in un potenziale a una dimensione:
(
0 x<0
V (x) =
V0 x > 0,
V
p
0
0
0
dove V0 è una costante positiva. Il pacchetto è
inizialmente localizzato a sinistra dell’origine ed ha un momento medio p0 > 0 . Descrivere
qualitativamente l’evoluzione del pacchetto. Determinare le autofunzioni nei due casi
W > V0 e W < V0 . Nell’ipotesi di pacchetto molto concentrato attorno a p0 applicare
il metodo della fase stazionaria per studiare analiticamente il moto del pacchetto.
7.13) Sia data una particella monodimensionale
immersa nel potenziale
V (x) = −αx
,
0
α>0.
Calcolare la dipendenza temporale della
indeterminazione ∆p dell’impulso.
7.14) Una particella a spin 1/2 e momento magnetico µ , è immersa nel campo magnetico:
B = B0 ẑ+B1 cos ωt x̂−B1 sin ωt ŷ con {x̂, ŷ, ẑ} versori, e di essa consideriamo solo i gradi
di libertà di spin. Se al tempo t = 0 la particella ha spin sz = +~/2 , qual’è la probabilità
di trovarla al tempo t > 0 con sz = −~/2 ? Discutere in particolare il caso |B1 /B0 | 1 ,
stabilendo per quale valore di ω0 questa probabilità ha un comportamento risonante.
[Definito ψ T (t) = |a(t) b(t)| , porre a(t) = α(t) exp[ iω0 t] e b(t) = β(t) exp[−iω0 t] ,
con ω0 = µB0 /~ , e per le nuove incognite cercare una soluzione esponenziale .]
7.15) Come il 7.14), ponendo: a(t) = A(t) exp[ iω/2 t] e b(t) = B(t) exp[−iω/2 t] Cosı̀
facendo, ci si riconduce a un’Hamiltoniana indipendente dal tempo.
7.16) Come il 7.14), risolvendo in rappresentazione di interazione.
7.17) Un oscillatore armonico monodimensionale si trova a t = 0 nello stato
46
7. EVOLUZIONE TEMPORALE. PROBLEMI.
ψ(x) = N exp [−β 2 (x − x0 )2 /2 ] con β e x0 costanti reali. Calcolare l’indeterminazione
di posizione e momento lineare a un tempo t > 0 qualunque.
7.18) Lo stato di una particella immersa in una buca di potenziale di profondità infinita
e larghezza a ( 0 < x < a ) , è descritta all’istante t = 0 dalla funzione d’onda:
ψ(x) = A sin3 (πx/a) . Determinare la funzione d’onda a un istante t successivo, e
valutare dopo quanto tempo la particella ripassa per lo stato iniziale.
7.19) Sia data l’Hamiltoniana che descrive una particella di massa µ soggetta a un campo
di gravità H = p2 /2µ + µgz . (Vedi 1.15). Sapendo che lo stato della particella ad un
certo istante t0 è descritto dalla funzione d’onda
ψ(x, y, z, t0 ) = N exp −(x2 + y 2 + z 2 )/4σ + iκz
con κ reale positiva, valutare l’indeterminazione sulla posizione a un tempo t > t0 .
7.20) Una particella di massa µ è confinata in una regione monodimensionale 0 ≤ x ≤ a .
Al tempo t = 0 la sua funzione d’onda è data da:
r
πx i
πx
8 h
ψ(x; t = 0) = ψ0 (x) =
1 + cos
sin
.
5a
a
a
a) Valutare la funzione d’onda a un tempo t > 0 . b) Valutare l’energia media del sistema
al tempo t = 0 e al tempo t > 0 . c) Valutare la probabilità che la particella possa essere
trovata nella prima metà della buca ( 0 ≤ x ≤ a/2 ) al tempo t > 0 .
7.21) Sia data una particella di spin 1, soggetta all’Hamiltoniana H = A sx + B sy , con
s operatore di spin e A e B costanti reali. Calcolare i livelli energetici del sistema.
Calcolare il valore di aspettazione di sz al tempo t , nel caso che all’istante iniziale il
sistema sia in un autostato di sz con autovalore ~ .
7.22) Una particella di massa µ si muove in una buca infinita con 0 < x < a . All’istante
t = 0 la funzione d’onda della particella è data da: ψ0 (x) = N x(a − x) per 0 < x < a ,
e ψ0 (x) = 0 altrove. Esprimere la funzione d’onda ψ(x, t) al tempo t sotto forma di serie,
valutando esplicitamente i coefficienti dello sviluppo.
7.23) Come il problema precedente, con : ψ0 (x) = N (a/2 − | a/2 − x | ) per 0 < x < a ,
e ψ0 (x) = 0 altrove.
7.24) Al tempo t = 0 la funzione d’onda di un atomo di idrogeno è la seguente:
√
√
1 2 ψ100 + ψ210 + 2 ψ211 + 3 ψ21−1 ,
ψ(r, 0) = √
10
7. EVOLUZIONE TEMPORALE. PROBLEMI.
47
con gli indici riferiti ai numeri quantici {n, l, m} . Calcolare: i) il valore di aspettazione
dell’energia; ii) la probabilità di trovare il sistema con l = 1 , m = 1 , in funzione del
tempo; iii) la probabilità di trovare al tempo t = 0 l’elettrone a distanza inferiore a 10 −10
cm. dal protone (valutazione approssimata); iv) l’evoluto temporale ψ(r, t) .
7.25) Sia data l’Hamiltoniana:
H = â† â + λ (â2 + â†2 ) , λ reale .
Determinare lo spettro di H . Se al tempo t = 0 il sistema si trova nello stato fondamentale
di H0 = â† â , determinare lo stato al tempo t > 0 .
7.26) Un atomo di idrogeno è immerso in un campo magnetico debole B , diretto come
l’asse z . Se all’istante t = 0 il sistema si trova nello stato 2p , ed è autostato di Lx con
autovalore ~ , determinare il valore di aspettazione dello stesso operatore Lx al tempo
t > 0 . (Operare in rappresentazione di Schrödinger).
7.27) Un fascio di atomi di idrogeno eccitati nello stato
2s attraversa la zona compresa tra i piatti di un
z
condensatore, ove esiste un debole campo elettrico
v
E
uniforme E su di una lunghezza a . Gli atomi di
x
idrogeno hanno velocità v lungo l’asse x e il campo
a
0
E è diretto come z . Se gli atomi nello stato 2s
entrano tra i piatti all’istante t = 0 , determinare la funzione d’onda al tempo t < a/v .
Determinare inoltre la distribuzione di probabilità dei vari stati, al tempo t > a/v .
7.28) Sia dato un oscillatore armonico classico, inizialmente a riposo nel punto di equilibrio
stabile, soggetto alla forza esterna:


0


t
F (t) = F0

τ

F
0
t<0
0<t<τ
t
τ < t,
0
τ
con τ reale positivo. a) Determinare la legge oraria finale. Discutere il caso in cui τ è
molto minore del periodo naturale ω di oscillazione, e quello opposto in cui τ è molto
maggiore del periodo. [Passare all’incognita z(t) = dx(t)/dt + iωx(t) ].
b)Nel corrispondente problema quantistico, determinare la probabilità che il sistema, inizialmente nello stato fondamentale, si trovi nel nuovo stato fondamentale a tempi t > τ .
Discutere i due casi limite come nelle considerazioni classiche. [Si utilizzi la descrizione di
Heisenberg per l’operatore di annichilazione e si sfrutti l’idea degli stati coerenti].
48
7. EVOLUZIONE TEMPORALE. PROBLEMI.
7.29) Come il 7.27). Un atomo di idrogeno si trova nello stato 2p con mx = ~ . Al tempo
t = 0 si accende un campo magnetico diretto come z . Assumendo di poter trascurare
gli effetti dello spin dell’elettrone e i termini quadratici nel campo, calcolare la dipendenza
temporale del valore di aspettazione di Lx . (Operare in rappresentazione di Heisenberg).
Quanto deve essere l’intensità del campo magnetico affinchè l’interazione spin-orbita sia
effettivamente trascurabile. Esprimere la risposta in gauss.
7.30) Un fascio di neutroni viaggia con velocità v
dalla regione I , ove è completamente polarizzato
nella direzione +z , alla regione II dove è
acceso un campo magnetico B = B ex .
i) Assumendo che una data particella passa dalla
regione I alla regione II al tempo t = 0 , quale
è la funzione d’onda di spin di quella particella
a t > 0 ? ii) In funzione del tempo, quale è la
polarizzazione del fascio nella regione II nelle
direzioni +x , +y e +z ?
z
I
II
s
B
v
x
0
y
7.31) Sia dato un oscillatore armonico forzato, descritto dall’Hamiltoniana:
H = H0 + H1 (t) =
p2
1
+ µω 2 x2 − x f (t) .
2µ 2
Al tempo t = 0 il sistema si trovi in un autostato | n i dell’Hamiltoniana imperturbata
H0 . In rappresentazione di interazione, trovare la probabilità di trovare il sistema in un
altro autovettore | m i di H0 , con m 6= n .
7.32) Siano date l’hamiltoniana H e l’osservabile A di un certo sistema:
0 1 0
1 0 0 w A = α 0 0 0 H = √ 1 0 1 .
2 0 1 0
0 0 −1
Se al tempo t = 0 lo stato del sistema è autostato di A con autovalore α , si determini la
probabilità che la misura di A al tempo t > 0 dia ancora il valore A = α . Si determini
la probabilità dello stesso evento nel caso in cui si sia effettuata la misura dell’energia in
un tempo intermedio 0 < τ < t .
7.33) L’Hamiltoniano di un oscillatore con frequenza variabile nel tempo dato da:
H = ω(t) â† â + µ(t) (â + â† )
ω(0) = 1 ,
µ(0) = 0 .
Si consideri lo stato iniziale dato da | ψ(0) i = | z i essendo | z i autostato di â con
√
autovalore z . Si determini al tempo t > 0 : i) il valore medio di x = (â + â† )/ 2 , ii) il
valore medio dell’energia h H(t) i . [Utilizzare la descrizione di Heisenberg].
7. EVOLUZIONE TEMPORALE. PROBLEMI.
49
7.34) Una particella di massa µ si trova in una buca infinita di larghezza L . Assumendo
che la particella sia nello stato fondamentale e che al tempo t = 0 la buca venga trasformata
in modo infinitamente rapido in una nuova buca di ampiezza 2L , calcolare: i) la probabilità
che la particella si trovi nello stato fondamentale della nuova buca di potenziale, ii) il valor
medio dell’energia all’istante t > 0. Discutere come cambierebbero le risposte alle domande
i) e ii) nel caso che la transizione L → 2L avvenga in modo adiabatico, cioè in un tempo
molto lungo rispetto alla scala di tempi caratteristici della dinamica del sistema.
7.35) Un elettrone con lo spin diretto lungo l’asse z positivo attraversa un campo magnetico
B diretto come l’asse x . Dopo un tempo τ si misura nuovamente il suo spin. Quale è
la probabilità di trovare lo spin capovolto? Questa probabilità può essere uguale a 1 ?
7.36) Una particella di massa µ è soggetta al potenziale V = 1/2 µω 2 x2 , e al tempo
t = 0 è descritta dalla funzione d’onda:
X 1 n
√
ψ(x, 0) = N
ψn (x) ,
2
n
essendo ψn gli autostati dell’energia relativi agli autovalori Wn = (n+1/2) ~ω . Calcolare
la costante di normalizzazione N . Trovare il valore d’aspettazione dell’energia a t = 0 .
Trovare una espressione di ψ(x, t) per t > 0 . Mostrare che | ψ(x, t) | 2 è una funzione
periodica del tempo, e valutarne il periodo.
7.37) Un elettrone si trova con lo spin diretto verso l’asse z negativo. All’istante t = 0 , si
accende un campo magnetico B omogeneo e costante, diretto come l’asse x . Determinare
al tempo τ > 0 le probabilità relative a due misure dello spin lungo z e lungo l’asse x .
7.38) Il vettore di stato al tempo t = 0 di una particella immersa in un potenziale di
oscillatore armonico V = 1/2 kx2 è dato da:
sin β
−α2 x2 /2
ψ(x, 0) = N e
cos β H0 (αx) + √ H2 (αx) .
2 2
√
N e β sono costanti reali, α2 = µk/~ , e i polinomi di Hermite sono cosı̀ normalizzati:
√
Z ∞
π n
2
−α2 x2
2 n! .
dx e
| Hn (αx) | =
α
−∞
i) Scrivere una espressione per ψ(x, t) . ii) Quali sono i possibili risultati di una misura
dell’energia al tempo t , e quali sono le relative probabilità? iii) Quanto vale < x > al
tempo t ?
7.39) Una particella monodimensionale si muove in una buca infinita, nulla per 0 ≤ x ≤ a
e infinita altrove. La sua funzione d’onda all’istante iniziale è data da:
r h
πx i
8
πx
1 + cos( ) sin( ) .
ψ(x, t = 0) =
5a
a
a
50
7. EVOLUZIONE TEMPORALE. PROBLEMI.
a) Valutare la funzione d’onda al tempo t0 > 0 . b) Valutare l’energia media del sistema
al tempo t = 0 e al tempo t > 0 . c) Valutare la probabilità che al tempo t > 0 la
particella si trovi nella metà sinistra della buca, cioè con 0 ≤ x ≤ a/2 .
7.40) Siano date due particelle distinguibili di spin ~/2 . Valutare le probabilità che una
misura del quadrato dello spin totale S = S1 + S2 dia come risultato 2~2 nei casi in
cui gli spin delle due particelle puntano: i) entrambi nella direzione +z ; ii) quello della 1
nella direzione +z e quello della 2 nella direzione −z ; iii) quello della 1 nella direzione
+x e quello della 2 nella direzione +z .
Le due particelle interagiscono tramite l’Hamiltoniana: Ĥ = ω/~ S1 ·S2 . All’istante t = 0 ,
lo spin della particella 1 punta nella direzione +z e quello della particella 2 nella direzione
−z . A un generico istante t > 0 , valutare : i) lo stato del sistema; ii) la probabilità di
trovare z1 = + , cioè la prima particella con lo spin in su; iii) il valore di aspettazione della
componente z dello spin della particella 1.
7.41) Sia dato un oscillatore tridimensionale isotropo: H = p2 /2µ + 1/2 µ Ω2 r2 .
a) Trovare i primi tre livelli dell’energia, W0 , W1 , W2 . b) Se il sistema viene perturbato
con un campo magnetico B uniforme costante, valutare come viene perturbato il terzo
livello W2 . c) Nel caso che a t = 0 venga accesa la perturbazione H 0 = A x cos ωt ,
determinare tra quali stati del punto a) possono avvenire transizioni. d) Con riferimento al
punto c), se lo stato iniziale imperturbato è quello fondamentale, valutare la probabilità di
transizione verso W1 al tempo t . e) Per valori di ω e Ω molto grandi rispetto alle altre
grandezze in gioco, dire per quali valori di queste la probabilità è sensibilmente diversa da
zero. Valutarla in questo caso, e nel caso che anche t sia grande.
7.42) Una particella di spin 1/2 è immersa in un campo magnetico diretto lungo z . A
partire dall’istante t = 0 si eseguono a intervalli regolari di tempo τ misure ripetute dello
spin nella direzione x . Dopo N misure oltre la prima, determinare: 1) la probabilità delle
differenti configurazioni e come queste si caratterizzano; 2) quali condizioni determinano
l’esistenza di configurazioni deterministiche.
7.43) Determinare la variazione nel tempo della funzione d’onda di un rotatore piano che
all’istante iniziale si trova nello stato: Ψ(ϕ; t = 0) = N sin 2 (ϕ) . Trovare il periodo del
rotatore.
7.44) Determinare la variazione nel tempo della funzione d’onda di un rotatore tridimensionale che all’istante iniziale si trova nello stato: Ψ(ϑ, ϕ; t = 0) = N cos 2 (ϑ) . Trovare il
periodo del rotatore.
7. EVOLUZIONE TEMPORALE. PROBLEMI.
51
52
7. EVOLUZIONE TEMPORALE. PROBLEMI.
CAPITOLO 8
Perturbazioni dipendenti dal tempo. Problemi.
8.1) Una particella, inizialmente in un autostato
dell’energia di una buca quadrata infinita,
è soggetta a una perturbazione della forma
V0 x cos(ωt) . Mostrare quali transizioni
tra autostati um e un sono possibili.
xVo
0
t
8.2) Ricavare le regole di selezione per le transizioni di dipolo elettrico in un oscillatore
armonico monodimensionale.
8.3) E’ dato un oscillatore armonico lineare di frequenza ν . Al tempo t = 0 si trova nel suo
stato fondamentale e, a partire da questo istante, è soggetto alla forza F = F 0 cos(2πν̄t)
con ν 6= ν̄ . Trovare al tempo t la probabilità di transizione verso uno stato eccitato.
8.4) Sia dato un oscillatore armonico inizialmente nello stato fondamentale descritto in
opportune unità di misura da H0 = 1/2 (p2 + q 2 ) . All’istante t = 0 l’oscillatore è
sottoposto alla perturbazione HI = λ q sin ω̃t . a) Si determini quale la probabilità
P (W, t) di misurare un’energia W = n + 1/2 ad un qualsiasi istante t > 0 . b) Al
tempo τ = 2π/ω̃ la perturbazione viene spenta. Dire se la probabilità P (W, t) dipende
dal tempo per t > τ . c) Confrontare con il risultato esatto del 7.32).
8.5) Discutere l’oscillatore armonico quantistico avente massa µ e frequenza ω soggetto
a una perturbazione esterna che ne modifica la frequenza in modo tale da avere


ω
ω(t) = ω + δω

ω
t<0
0<t<T
T <t.
Se l’oscillatore si trova nello stato fondamentale per t < 0 , quale sarà la probabilità di
misurare un’energia pari a (n + 1/2) ~ω a un tempo maggiore di T ?
8.6) Una particella tridimensionale di massa µ e carica q è soggetta al potenziale armonico
isotropo: V (x) = K/2 (x2 + y 2 + z 2 ) . All’istante t = −∞ l’oscillatore è nel suo stato
fondamentale e viene perturbato dal un campo elettrico: E(t) = A exp[−(t/τ )2 ] ẑ , con ẑ
53
54
8. PERTURBAZIONI DIPENDENTI DAL TEMPO. PROBLEMI.
versore dell’asse z , A e τ costanti e A 1 . Al primo ordine perturbativo, calcolare
la probabilità che a t = +∞ l’oscillatore si trovi in uno stato eccitato .
8.7) Un atomo di idrogeno si trova nel suo stato fondamentale. Al tempo t = 0 viene acceso
un campo elettrico spazialmente uniforme dato da: E(t) = E0 exp[−t/τ ]. Determinare lo
stato dell’atomo ad un tempo t τ , valutando esplicitamente il primo coefficiente non
nullo in teoria delle perturbazioni dipendenti dal tempo.
8.8) Supponendo che l’Hamiltoniana H0 abbia spettro discreto, determinare la probabilità
di transizione dal livello n al livello k imperturbati, per un sistema sotto l’effetto delle
seguenti perturbazioni. i) Accensione istantanea: V (t) = V0 θ(t) , con θ(t) gradino
di Heaviside ( dθ(t)/dt = δ(t) ), e V0 indipendente dal tempo. ii) Impulso istantaneo:
V (t) = V0 δ(t) , con V0 indipendente dal tempo. Quali sono le condizioni di applicabilità
delle formule ottenute nel caso che i) oppure ii) si instaurino in un tempo finito τ ?
8.9) Una particella di massa µ = 0.511M eV si trova in [0, a] nello stato fondamentale
di una buca infinita di larghezza a = 1 Å. Al tempo t = 0 si attiva istantaneamente
un potenziale a buca quadrata, centrato in x = a/2 di profondità V0 = −104 eV e
larghezza 2b = 10−12 cm , che viene rimosso al tempo τ = 5·10−18 sec . Dopo la rimozione
della perturbazione, quale è la probalità di trovare il sistema in ciascuno dei primi tre stati
eccitati della buca infinita?
8.10) Una particella monodimensionale a carica negativa −e è immersa in una buca
di potenziale infinita per −a/2 < x < a/2 e si trova nel primo autostato dell’energia.
All’istante iniziale viene applicato un campo elettrico E diretto nel verso positivo delle
x , che viene poi rimosso al tempo τ > 0 . i) Con la teoria delle perturbazioni dipendenti
dal tempo, valutare le probabilità P2 e P3 che la particella si trovi al tempo t > τ
negli autostati della buca infinita con n = 2 e n = 3 , rispettivamente. ii) Dire se ci si
attende che queste probabilità dipendono da t . iii) Specificare le condizioni sui parametri
che giustificano l’approssimazione perturbativa.
8.11) Un elettrone è confinato in una scatola cubica di lato 2a . Da t = 0 in poi al sistema
si applica il campo elettrico uniforme: E = E0 e−α t , con α > 0 e E0 perpendicolare a
una delle facce della scatola. Al primo ordine in E0 valutare la probabilità di transizione
dallo stato fondamentale a t = 0 al primo stato eccitato al tempo t = ∞ .
8.12) Un atomo di idrogeno è immerso nel campo elettrico omogeneo di intensità :
E(t) = (E/πe) τ /(t2 + τ 2 ) , con E e τ costanti. Se a t = −∞ l’atomo si trova nello
stato fondamentale, quale è la probabilità di trovarlo nello stato 2p a t = ∞ ?
8. PERTURBAZIONI DIPENDENTI DAL TEMPO. PROBLEMI.
55
8.13) Una particella si trova al tempo t → −∞ nello stato fondamentale di una buca
infinita di larghezza a . Su di essa si esercita anche un potenziale variabile nel tempo, che
può assumere una delle seguenti forme: a) H1 (x, t) = −xV0 exp[−t2 /τ 2 ] ;
b) H1 (x, t) = −xV0 exp[−|t|/τ ] ; c) H1 (x, t) = −xV0 /[1 + (t/τ )2 ] . Al primo ordine delle
perturbazioni, calcolare le diverse probabilità di transizione della particella a stati eccitati
per t → +∞ . Indicare anche le condizioni di applicabilità dell’approssimazione.
8.14) Un rotatore piano di momento bipolare d , vedi 2.4), si trova nel suo stato fondamentale fintanto che non agisce un debole campo elettrico omogeneo di intensità E(t) = E(t) n ,
situato nel piano di rotazione e con:
(
0
t<0
E(t) =
E0 exp[−t/τ ] t > 0 .
Per t → ∞ e al secondo ordine della teoria delle perturbazioni dipendenti dal tempo, calcolare le probabilità di transizione proibite al primo ordine. Paragonarle con queste, e indicare
le condizioni di applicabilità dell’approssimazione. [ V = −d · E(t) = −d E(t) cos ϕ .]
56
8. PERTURBAZIONI DIPENDENTI DAL TEMPO. PROBLEMI.
CAPITOLO 9
Momento angolare e spin. Problemi.
9.1) Considerare una particella nello stato descritto da
ψ = N ( x + y + 2z ) e−αr ,
con N costante di normalizzazione. Indicare quali sono i possibili risultati di una misura
della terza componenete del momento angolare Lz , e quali le rispettive probabilità.
9.2) Sia dato un sistema descritto dall’Hamiltoniana:
H = p2 + a (x2 + y 2 ) + b z 2 .
i) Se eseguo una misura di H e immediatamente dopo una misura di L2 e dopo ancora
nuovamente di H , ritrovo necessariamente lo stesso valore dell’energia? ii) Come sopra
nel caso a = b . iii) Nel caso a = b , dopo una misura solo di L2 il vettore di stato si
trova necessariamente in un autostato dell’energia?
9.3) Al tempo t = 0 la funzione d’onda di una particella ha la forma ψ = N xye−r ,
p
dove r = x2 + y 2 + z 2 e N è una costante di normalizzazione. i) Quali sono i possibili
risultati di una misura del momento angolare L2 e di Lz e quali le loro probabilità? ii)
Se la particella si trova in un potenziale centrale, come variano tali probabilità nel tempo?
9.4) L’Hamiltoniana di un sistema di due spin è data da:
H = α S1 · S2 + β (S1z + S2z )
Calcolare lo spettro dell’energia per gli spin uguali a: i) {1/2, 1/2} , ii) {1/2, 3/2} .
9.5) Un sistema costituito da due particelle di spin 1/2 è descritto dalla funzione di spin
ψ(1, 2) = χ+ (1)χ− (2), dove χ± (i) , i = 1, 2 sono autofunzioni della componente lungo z
dello spin della particella i-esima. i) Se si esegue una misura di (S1 + S2 )2 , quali risultati
si possono ottenere e con quali probabilità? ii) Quale è il valor medio della componenente
lungo l’asse z dello spin totale del sistema?
9.6) Mostrare che la funzione ψ = N z exp[−α (x2 + y 2 + z 2 ) ] , con N costante di
normalizzazione, è autostato di L2 e di Lz . Ricavare le altre autofunzioni di Lz
appartenenti alla stessa rappresentazione irriducibile dell’algebra {Lx , Ly , Lz } .
57
58
9. MOMENTO ANGOLARE E SPIN. PROBLEMI.
9.7) Una particella di spin 1/2 , inizialmente in
un autostato di Sz con autovalore ~/2 , entra
dalla direzione y in un apparato di Stern-Gerlach
orientato per misurare il momento angolare in
una direzione sul piano x − z individuata
dall’angolo θ .
Calcolare le probabilità di ottenere i valori ±~/2 .
z
θ
⊕
y
x
9.8) La funzione d’onda di una particella è della forma ψ = f (r, θ) cosϕ . Cosa si può
predire circa il risultato di una misura della componente z del suo momento angolare?
9.9) Una particella di spin 1, si trova in un autostato di Sz . Valutare i valori di aspettazione
per Sx , Sy , Sx2 , Sy2 in corrispondenza ai diversi autovalori.
9.10) Una particella sulla sfera, descritta dalla Hamiltoniana H = L2 /2I + a Lz , con I e
a costanti numeriche, è caratterizzata dallo stato iniziale: ψ(0) = A sin 2θ sin ϕ , con A
costante di normalizzazione. Dimostrare che al generico istante t lo stato della particella è
dato da: ψ(t) = A exp[−i3~ t/I] sin 2θ sin(ϕ − at) .
9.11) Senza fare ricorso alla teoria generale dell’addizione di momenti angolari, determinare
autostati e autovalori relativi agli operatori S2 e Sz , essendo S = s1 + s2 , in termini
degli autostati | 1/2 ; ±1/2 ii degli operatori s2i e szi (i=1,2).
9.12) Per una particella di spin 1/2 si è osservata la proiezione dello spin sull’asse z , e si
è trovato il valore ~/2 . Calcolare: a) la probabilità di trovare lo stesso valore immediatamente dopo la prima misura per la proiezione di S sugli assi x , y e sull’asse r di
coseni direttori l, m, n ( l2 + m2 + n2 = 1 ); b) i valori medi delle proiezioni di S sugli
stessi assi x, y e r ; c) gli scarti quadratici medi delle proiezioni di S sugli assi x e y .
d) Se la seconda misura viene eseguita dopo un certo intervallo di tempo dalla prima e la
particella è libera, dire se sono variate le probabilità e i valori medi sopra considerati.
9.13) La funzione di spin di un sistema di N particelle a spin 1/2 è della forma:
1 1
1 0
0 0 ψ = ... ... .
01 02
0 n 1 n+1 1 n+2
1N
Valutare il valor medio del quadrato dello spin totale del sistema.
9.14) Dati N spinori ( s = 1/2 ) diversi tra di loro, calcolare quanti stati linearmente
indipendenti corrispondono all’autovalore Sz della terza componente dello spin totale.
9. MOMENTO ANGOLARE E SPIN. PROBLEMI.
59
9.15) Determinare lo stato a spin totale 0 , in funzione di due vettori di stato a spin 1 .
9.16) Sia data la funzione d’onda di due particelle di momento angolare j della forma:
P
ψ = (2j + 1)−1/2 jmj =−j (−)sj | j, mj i1 | j, −mj i2 ,
con sj = mj per j intero e sj = mj + 1/2 per j semintero. Dimostrare che tale stato
ha momento angolare totale zero.
9.17) Sia dato un sistema di due particelle (distinguibili) di spin 1 . Senza fare uso dei
coefficienti di Clebsch-Gordan, ricavare le autofunzioni dello spin totale e della sua terza
componente in funzione degli autostati di particella singola.
9.18) Due particelle di spin j1 e j2 si trovano nello stato jtot = mtot = j1 + j2 − 1 .
Determinare la probabilità di misurare m1 = j1 .
9.19) Una particella di spin 1/2 si trova nello stato ψ = | sin α i cos α |T . Calcolare la
probabilità che la misura di n̂ · s con n̂ = {n, m, l} dia il valore ±1/2 . Vedi 9.12).
9.20) Due particelle, di spin 1 e 1/2 , si trovano in uno stato a spin totale | 1/2, 1/2 i T .
Detti S1 e S2 gli operatori di spin 1 e 1/2 , rispettivamennte, valutare le probabilità
di misurare i valori possibili di S2z , S2y . Se in una prima misura di S2y si è trovato il
valore 1/2 , valutare le probabilità legate a successive misure di S1y .
9.21) Un oscillatore armonico tridimensionale isotropo è descritto all’instante t = 0 da:
ψ(x, y) = N Z(z) exp[−α(x − x0 )2 − β(y − y0 )2 + ik1 x + ik2 y ] ,
con Z(z) arbitrario normalizzato. Determinare il valore di aspettazione della componente
z del momento angolare a un tempo qualunque t > 0 .
9.22) Sia dato un sistema descritto dall’Hamiltoniana H = λ (L+ L− )2 e dalla funzione
d’onda all’istante iniziale ψ(0) = A sin θ sin ϕ . Determinare l’evoluzione temporale della
funzione d’onda e valutare a quale tempo essa diventa ψ(t) = A sin θ cos ϕ .
9.23) Una particella di massa µ senza spin si trova all’istante t = 0 nello stato:
z d
sin kr
ψ(x, y, z) = N
,
r dr
kr
p
con r = x2 + y 2 + z 2 . Si determinino i valori di aspettazione per la componente z del
momento angolare h Lz i , per il suo quadrato h L2 i e per l’energia cinetica h p2 /2µ i .
60
9. MOMENTO ANGOLARE E SPIN. PROBLEMI.
9.24) Si consideri il sistema composto da due particelle con spin ~/2 e momento magnetico
dato rispettivamente da µe σ e e µp σ p . L’hamiltoniano è dato da:
H = H0 + (µe σez + µp σpz )B + C σ e · σ p ,
dove B rappresenta un campo magnetico esterno costante diretto come l’asse z , C è una
costante positiva e H0 rappresenta la parte di hamiltoniano che non dipende dallo spin.
Quali sono gli autovalori dell’energia e quali le autofunzioni, limitatamente alla dipendenza
dallo spin? [ Separare le variabili e omettere H0 . ]
9.25) Un sistema di tre particelle di spin 1/2 possiede otto stati di spin linearmente
indipendenti. Determinare quali sono autostati degli operatori di spin totale S 2 e Sz .
9.26) Nello spazio di spin le rotazioni di un angolo β attorno all’asse y sono date
dall’operatore: Ry (β) = exp[−iβSy ] . Trovarne la rappresentazione matriciale nel caso di
s = 1/2 e s = 1 , con lo sviluppo in serie, e con lo sviluppo spettrale.
9.27) Dati due momenti angolari uguali l1 = l2 = l , determinare lo stato a momento angolare totale L = 0 nella rappresentazione prodotto diretto | l, m1 i | l, m2 i . [Utilizzare
l’operatore innalzatore L+ .]
9.28) Si consideri una particella in campo centrale, la cui funzione è data da:
ψ(r, θ, ϕ) = N f (r) cosn θ ,
con n intero e N costante di normalizzazione. Dimostrare che nel limite n → ∞
l’indeterminazione sulle componenti x, y del momento angolare tende all’infinito, mentre la posizione angolare della particella risulta sempre
l’asse z .
meglio collimata lungo
±iϕ
[Utilizzare l’espressione degli operatori: L± = ~ e
±∂/∂θ + i cot θ ∂/∂ϕ .]
9.29) Dati due momenti angolari uguali j1 = j2 = j , mostrare che gli autostati del
momento angolare totale J 2 e Jz con J = J 1 + J 2 , in termini del prodotto diretto
dei singoli momenti angolari, sono a simmetria definita nello scambio m1 ↔m2 . Dire quali
sono pari e quali dispari.
9.30) Una particella si trova in uno stato descritto dalla funzione d’onda:
Z ∞
ψ(x) = A cos θ + sin θ(1 + 2 cos θ) sin ϕ g(r) ,
dr r 2 | g(r) |2 = 1 .
0
2
Quali sono i possibili risultati di una misura di Lz e di L ? Quali sono le probabilità
relative? Quali soni i valori di aspettazione di Lz e di L2 ?
9. MOMENTO ANGOLARE E SPIN. PROBLEMI.
61
9.31) Due elettroni sono strettamente legati in due siti differenti in un solido e possono
pertanto essere trattati come distinguibili. Essi interagiscono con l’Hamiltoniana:
H = −β σ1x σ2x +σ1y σ2y , con β costante. i) Quanti livelli di energia possiede il sistema?
Quali sono le loro energie e le degenerazioni? ii) Se si aggiunge un campo magnetico B
nella direzione z , quali diventano i nuovi livelli di energia?
9.32) Tre particelle di spin ~/2 si trovano in equilibrio ai vertici di un triangolo equilatero.
L’interazione tra gli spin determina l’Hamiltoniana: H = β (s1 · s2 + s2 · s3 + s3 · s1 ) dove
β è una costante. Si determini lo spettro di energia e se ne discuta la degenerazione. Se si
accende un campo magnetico uniforme B ortogonale al piano che contiene le particelle,
trovare il valore minimo del campo per il quale esiste un livello di energia pari a zero.
9.33) Si consideri l’energia di accoppiamento di quattro spin s1 , s2 , s3 , s4 posti ai vertici
P
di un tetraedro H = −µ i,j si ·sj . Calcolare lo spettro dell’energia nel caso in cui ciascuno
spin abbia valore ~/2.
√
9.34) Sia data una coppia {e− , e+ } nello stato di puro spin |ψ i = 1/ 2 ( |+− i−|−+ i ).
Calcolare il valore di aspettazione di (n1 · s1 )(n2 · s2 ) , con n1 e n2 versori arbitrari.
9.35) Una particella senza spin è rappresentata dalla funzione d’onda (vedi 9.1)):
ψ = N (x + y + 2z) e−αr , con r 2 = x2 + y 2 + z 2 , e α reale. Trovare il valore
di aspettazione del momento angolare totale e della sua terza componente. Calcolare la
probabilità di trovare la particella nell’angolo solido dΩ individuato dagli angoli θ e ϕ .
9.36) Una particella è immersa in un potenziale centrale, e ha numeri quantici di momento
angolare orbitale l = 2 e di spin s = 1 . Trovare i livelli di energia e le degenerazioni
associate a una interazione spin-orbita della forma Hso = β L · S con β costante reale.
(1)
9.37) Due particelle di spin 1/2 si trovano una nello stato con sz = 1/2 e l’altra con
(2)
sx = 1/2 . Quale è la probabilità di trovare il valore S = 0 per lo spin totale?
9.38) Consideriamo una particella a spin 1/2 . Essendo sy e sz gli operatori di momento
angolare s = ~/2 σ , e A e B due costanti reali, quali sono gli autovalori e gli
autovettori normalizzati dell’operatore S = Asy + Bsz ? Se il sistema si trova nello stato
corrispondente all’autovalore superiore di S , quale è la probabilità che una misura di sy
dia come risultato ~/2 ?
9.39) Sia data una particella con momento angolare orbitale l e spin 1/2 . In funzione
degli stati prodotto diretto | l, ml ; s, ms i , determinare gli stati di momento angolare
62
9. MOMENTO ANGOLARE E SPIN. PROBLEMI.
totale | j / m i con m = l − 1/2 , utilizzando esplicitamente gli operatori di creazione e
distruzione J± | j / m i = [ j(j + 1) − m(m ± 1) ]1/2 | j / m ± 1 i , ( ~ = 1 ) .
9.40) Un atomo di idrogeno si trova nello stato 2 P1/2 ( n = 2, l = 1, j = 1/2 ). i) Quale
è la probabilità che lo spin si trovi in direzione opposta a quella del momento angolare
totale? Vedi 9.20). ii) Calcolare la densità di probabilità P (θ, ϕ) che l’elettrone si trovi
nell’angolo solido θ, ϕ , indipendentemente dalla distanza radiale e dallo spin.
9.41) Si consideri lo stato | l, m > , autostato degli operatori L2 e Lz , con:
L2 | l, m >= l(l + 1)~2 | l, m > ,
Lz | l, m >= m~ | l, m > .
Su questi stati, calcolare i valori di aspettazione < Lx > e < L2x > .
9.42) Un iperone Ω− (3/2, +) , (spin, parità intrinseca), può decadere via interazioni
deboli in un iperone Λ (1/2, +) e in un mesone K − (0, −) : Ω− → Λ + K − .
i) Supponendo il decadimento a riposo, determinare la forma più generale della distribuzione angolare del mesone K − relativa alla direzione z lungo la quale la Ω− ha
componente massima dello spin, assumendo cioè come stato iniziale | Ω−
3/2,3/2 > .
ii) Quale sarebbe invece la distribuzione se la parità venisse conservata?
9.43) Consideriamo le reazioni: a) π + p → π + p , b) π − p → π − p , c) π − p → π 0 n .
Queste reazioni possono avvenire per interazioni forti che conservano lo spin isotopico, e
possono formare una risonanza ∆ a spin isotopico I = 3/2 oppure una N ∗ a spin
isotopico I = 1/2 . Tenendo conto che all’energia di una risonanza si può trascurare il
contributo dell’altro canale, valutare il rapporto delle tre sezioni d’urto per i due casi.
9.44) Un fascio di particelle con momento angolare l = 1 si muove lungo una direzione che
indicheremo come asse y e attraversa un magnete Stern-Gerlach avente campo magnetico
in una direzione giacente nel piano ortogonale al movimento, e che chiameremo asse x .
Il fascio emergente risulta separato in tre componenti, corrispondenti a m = −1, 0, 1 , e
la componente m = 1 viene fatta passare attraverso un altro Stern-Gerlach con campo
magnetico lungo l’asse z. a) In quanti fasci si separa ulteriormente il fascio con m = 1 ,
e qual’è il loro numero relativo di atomi? b) Stesse domande per le altre due componenti
m = 0, −1 del fascio originario. c) Se consideriamo il fascio uscente con m0 = 1 dal
secondo Stern-Gerlach, possiamo affermare che le componenti x e z del suo momemto
angolare sono uguali a ~ ? Giustificare la risposta.
9. MOMENTO ANGOLARE E SPIN. PROBLEMI.
63
64
9. MOMENTO ANGOLARE E SPIN. PROBLEMI.
CAPITOLO 10
Molte particelle. Problemi.
10.1) Sia dato un atomo di elio in cui uno degli elettroni è stato sostituito da un muone
(stessa carica, massa 207 volte superiore). Si trovi un valore approssimato per lo spettro
dello stato fondamentale trascurando l’interazione e− µ− , e si discutano le differenze dal
caso di due elettroni. Si determini un’approssimazione migliore tenendo conto dell’effetto
di schermo che il muone esercita sul nucleo; si spieghi infine per quale motivo gli stati con
numero quantico principale del muone nµ > 1 sono instabili per ionizzazione.
10.2) Due particelle monodimensionali di massa µ1 e
µ2 si muovono nel potenziale:
(
0
|x12 | ≤ a
V =
x12 = x1 − x2 .
∞ |x12 | > a
Trovare autovalori e autofunzioni di questo
sistema nel caso di momento totale P , nella
ipotesi che le due particelle siano bosoni
indistinguibili o fermioni indistinguibili ( µ1 = µ2 ).
−a
0
a
10.3) Due fermioni identici di spin 1/2 interagiscono mediante il potenziale armonico:
V = K/2 (x1 − x2 )2 + V0 s1 · s2 ,
ove x1 , x2 , s1 , s2 , indicano gli operatori di posizione e di spin delle due particelle.
Determinare autovalori e autofunzioni del sistema.
10.4) Per l’atomo di Elio, valutando la repulsione coulombiana al primo ordine perturbativo,
calcolare le energie di legame e i potenziali di ionizzazione dello stato fondamentale e dei
primi stati eccitati, singoletto e tripletto, 2 1S e 2 3S . [ Per gli integrali diretti e l’integrale di
scambio utilizzare i valori (vedi l’Appendice): J1,0,0;1,0,0 = 5/4 Zw0 , J1,0,0;2,0,0 = 34/81 Zw0 ,
K1,0,0;2,0,0 = 32/729 Zw0 . ]
10.5) Un atomo di tre elettroni si trova nello stato fondamentale imperturbato (1s) 2 2s .
i) Scrivere la funzione d’onda dello stato sotto forma di determinante di Slater. ii) Esprimere
le correzioni all’energia dovute alla repulsione coulombiana tra gli elettroni, al primo ordine
perturbativo e tramite le sole funzioni d’onda orbitali u100 (ri ) e u200 (ri ) (i = 1, 2) .
65
66
10. MOLTE PARTICELLE. PROBLEMI.
10.6) Due particelle identiche di massa µ e spin
1/2 si trovano in una scatola cubica di lato 2a .
i) Determinare lo stato fondamentale e trovare la
probabilità di trovare una particella in un volume
dx attorno al punto x .
ii) Se si aggiunge una interazione della forma
V = A σ 1 · σ 2 , determinare come viene
modificata l’energia dello stato fondamentale.
10.7) Tre particelle identiche di massa µ = 10.8 · 10−28 gr e spin 1/2 si muovono libere
in una scatola cubica di lato 2l = 2 · 10−8 cm . Calcolare le energie necessarie per passare
dallo stato fondamentale al primo eccitato, e da questo al secondo.
10.8) Scrivere la forma più generale dello stato fondamentale di un atomo di boro (numero
atomico 5), trascurando la repulsione coulombiana tra gli elettroni.
10.9) Tre bosoni identici con s = 1 sono descritti dalla funzione d’onda
Ψ = φ(x1 )φ(x2 )φ(x3 )Σ(σ1 , σ2 , σ3 ) ,
con φ(x) funzione data, e {σ1 , σ2 , σ3 } terze componenti dello spin di ciascuna particella.
Determinare il numero degli stati indipendenti. Da tale numero e da semplici considerazioni
di simmetria, determinare i valori possibili per lo spin totale. Scrivere esplicitamente gli
autostati dello spin totale e della sua terza componente in funzione degli autostati dello
spin delle singole particelle. E per tre spinori identici con s = 1/2 ?
10.10) Calcolare l’energia dello stato fondamentale dell’atomo di Litio, al primo ordine
spe
perturbativo nella repulsione Coulombiana, e confrontare con il valore sperimentale WLi
≈
−203.4 ev . (Vedi 10.5) e 10.4) per gli integrali.)
10.11) Calcolare l’energia dello stato fondamentale dell’atomo di Litio, repulsione Coulombiana inclusa, mediante il metodo variazionale, utilizzando come funzioni di prova:
ψ ζ = uζ1 (r1 ) uζ1 (r2 ) uζ2 (r3 ) χ ,
dove χ è la funzione di spin e uζ1,2 (r) sono le due prime autofunzioni di un atomo idrogenoide a numero atomico ζ inteso quale parametro variazionale. Confrontare
con i risultati perturbativi dell’esercizio 10.10). [Notare che l’uso di funzioni d’onda non
simmetrizzate non implica avere trascurato completamente l’identità delle particelle: il
principio di esclusione di Pauli è infatti implicito nella scelta delle funzioni di prova.]
10.12) Come il problema precedente, ma con funzioni di prova antisimmetrizzate.
10. MOLTE PARTICELLE. PROBLEMI.
67
10.13) Quale può essere lo spin totale S di due bosoni identici di spin s, in uno stato a
momento orbitale relativo L?
10.14) Due bosoni identici a spin zero sono descritti dalla funzione d’onda ψ(r1 , r2 ). Determinare la probabilità di trovare una particella in un intorno infinitesimo del punto r1 e
l’altra in un intorno infinitesimo del punto r2 . Controllare la coerenza di questo valore con
la condizione di normalizzazione della funzione d’onda. Determinare la probabilità che le
due particelle si trovino all’interno dello stesso volume V . Determinare la probabilità che
le due particelle si trovino una all’interno e l’altra all’esterno del volume V .
10.15) Siano date due particelle identiche interagenti tramite il potenziale:
V (x) = K/2 (r1 − r2 )2 . Qual’è la degenerazione rispettivamente dello stato fondamentale
e del primo stato eccitato nei casi di particelle di spin 0 , 1/2 , 1 ? Dire come cambia
la risposta se le particelle fossero invece sottoposte al potenziale: V (x) = K/2 (r 12 + r22 ) .
Dire inoltre in entrambi i casi se e come viene risolta la degenerazione con l’introduzione di
un campo magnetico costante lungo l’asse z . [Per l’oscillatore tridimensionale, vedi 3.6).]
10.16) Due particelle di massa µ in una scatola rettangolare di lati a > b > c interagiscono
tra di loro tramite il potenziale V = A δ3 (r1 −r2 ) , e si trovano nello stato di minima energia.
Al primo ordine perturbativo, calcolare l’energia del sistema nelle seguenti condizioni:
i) particelle non identiche; ii) particelle identiche a spin zero; iii) particelle identiche a spin
1/2 , con gli spin paralleli.
10.17) Tre particelle monodimensionali di massa µ sono legate l’una all’altra da forze
armoniche, date dal potenziale: V = k/2 [ (x1 − x2 )2 + (x2 − x3 )2 + (x3 − x1 )2 ] .
Utilizzando le coordinate del centro di massa: y1 = x1 − x2 , y2 = (x1 + x2 )/2 − x3 ,
y3 = (x1 + x2 + x3 )/3 , risolvere il problema agli autovalori in modo esatto.
10.18) Utilizzando il risultato precedente, trovare l’energia dello stato fondamentale nel
caso di tre bosoni identici a spin zero. Analogamente nel caso di tre fermioni identici di
spin 1/2 .
10.19) 1) Due particelle identiche, non interagenti tra di loro, sono immerse in un potenziale
armonico isotropo (vedi 3.6)). Calcolare le degenerazioni dei primi tre livelli dell’energia
nei seguenti casi: a) le due particelle hanno spin 1/2 ; b) le due particelle hanno spin 1 .
10.20) Calcolare le degenerazioni delle due configurazioni elettroniche: a) 2s2p , b) 2p3p .
, e verificare che il numero degli
Per ciascuna di queste elencare i valori possibili di L2S+1
j
stati in questa rappresentazione è uguale alle degenerazioni viste prima.
68
10. MOLTE PARTICELLE. PROBLEMI.
10.21) Due particelle sono immerse in un potenziale nullo per 0 < x < 2a e infinito altrove.
a) Quali sono i valori dei primi quattro valori dell’energia? b) Quali sono le degenerazioni
di queste energie nel caso che le due particelle siano: i) identiche, con spin 1/2 ; ii) non
identiche, entrambe con spin 1/2 ; iii) identiche, con spin 1 .
CAPITOLO 11
Argomenti vari. Problemi.
11.1) Consideriamo le seguenti affermazioni. i) I polinomi di Laguerre costituiscono un
insieme completo in L2 [ 0, ∞) sulla misura opportuna. ii) Le autofunzioni dell’atomo di
idrogeno relative agli stati legati non costituiscono un insieme completo in L2 [ 0, ∞) .
Sono esse contradditorie? Si, No, Perchè.
11.2) Una particella di massa µ vincolata sul segmento [ 0, a ] dell’asse x si trova in un
autostato dell’energia. Calcolare h x i e ∆x .
11.3) Costruire due matrici 3 × 3 tali che nessuna delle due costituisca un set completo
di osservabili, ma che lo sia l’insieme delle due.
11.4) Di un sistema fisico siano dati il
0 1
1 0
A = a 0 0
0 0
vettore di stato al tempo t e l’osservabile A :
1 0 0 1 1
0 0 | ψ i = .
0 −i
2 1 1 i 0
Determinare i risultati di una misura di A sullo stato | ψ i e le relative probabilità.
11.5) La costante elastica k di un oscillatore armonico
unidimensionale nel suo stato fondamentale
improvvisamente si raddoppia. Immediatamente dopo
questo evento, quale è la probabilità che una
misura di energia sul nuovo oscillatore lo trovi:
i) nello stato fondamentale; ii) nel primo stato
eccitato; iii) nel secondo stato eccitato.
11.6) Una particella di massa µ è soggetta a un potenziale armonico di frequenza ω . Ad
un certo istante essa è descritta dalla funzione d’onda:
ψ(x) = N x2 exp[−µωx2 /2~ ] .
Calcolare il valore medio dell’energia a tale istante.
69
70
11. ARGOMENTI VARI. PROBLEMI.
11.7) Dire se sullo stato
q √
h
i
2
2
ψo (x) = a/ π exp −a /2 (x − x0 ) + i/~ p0 (x − x0 )
vale la uguaglianza h p2 i = h p i2 , essendo p l’operatore momento.
11.8) Per una particella senza spin in tre dimensioni, considerare le osservabili φ , angolo
equatoriale, e Mz , terza componente del momento angolare. Determinare per esse un
√
principio di indeterminazione, e verificarlo sugli stati um (φ) = 1/ 2π exp(imφ) .
11.9) L’elettrone di un atomo di idrogeno si trova nel suo stato fondamentale. Calcolare la
distribuzione di probabilità per il momento.
11.10) Dato un pacchetto d’onde nel potenziale V = k x2 /2 + ax3 , si dimostri che i valori
medi h x i e h p i non soddisfano le equazioni classiche del moto, se non nel caso a = 0 .
11.11) Sia data la funzione d’onda di una particella libera in una dimensione:
q √ Z ∞
1
1
i
p2 ψ(x) = √
β/ π
dp exp − β 2 (p − p0 )2 + (px −
t) .
2
~
2µ
2π~
−∞
Calcolare la densitá di probabilitá che al tempo t , fatta una misura di energia, si trovi un
valore compreso tra W e W + dW .
11.12) Sia H l’hamiltoniano di un sistema, X un’osservabile commutante con H , e Y
un’altra osservabile soddisfacente a [H, Y ] = iX . i) Dimostrare che anche Z = i[X, Y ]
è costante del moto. ii) Fornire un esempio concreto dei tre operatori H, X, Y .
11.13) Un sistema di due particelle a spin zero si trova nello stato
Ψ(x1 , x2 ) = N exp −α/2 x21 − β/2 x22 + γ x1 · x2
Si calcoli il valore di aspettazione del momento lineare e delle componenti del momento
angolare delle due particelle.
11.14) In uno scattering elettrone-protone, scrivere la più generale funzione d’onda iniziale
dell’elettrone in campo coulombiano, tale che questo in nessun istante successivo possa
essere catturato in uno stato legato.
11.15) Determinare la parità intrinseca del π − dalla reazione forte π − + d → 2n ,
supponendo che questa avvenga dopo formazione dell’atomo mesico π − d in onda S .
11. ARGOMENTI VARI. PROBLEMI.
71
Ricordare che: l’operatore di parità è definito da P̂ ψα (x, σ) = ηα ψα (−x, σ), con ηα=±1
detta parità intrinseca della particella α ; le interazioni forti conservano la parità; il π −
ha spin zero; il deutone e il neutrone hanno spin-parità 1+ e 1/2+ , rispettivamente.
11.16) Siano Wn = Wn (µ, ω, λ, ~) gli autovalori dell’Hamiltoniana
p2
1
1
+ µω 2 q 2 + λq 4 ,
[ q, p ] = i~.
2µ 2
4
Dimostrare che vale la relazione:
1/3
~λ
Wn (µ, ω, λ, ~) = ~
Wn ( ω 3 µ2 /~λ ) .
µ2
H=
[Utilizzare una semplice trasformazione canonica oppure considerazioni dimensionali.]
11.17) Sia data l’Hamiltoniano per una particella tridimensionale di massa µ:
p2
+ V (q2 ) ,
V (q2 ) = k | q | 2β , k > 0 ,
2µ
e un operatore autoaggiunto A soddisfacente le regole di commutazione:
[ A, pk ] = i~ pk , [ A, qk ] = −i~ qk . Ricavare da queste le relazioni:
H=
p2
β
1
|W i=
W ,
h W | V (q2 ) | W i =
W ,
2µ
1+β
1+β
essendo H | W i = W | W i . Ricavare inoltre una espressione esplicita per A .
hW |
11.18) Risolvere il problema agli autovalori per l’operatore
1
K = ( p4 + q 4 )
2
essendo p, q operatori canonici. Adottare una approssimazione che consista nel proiettare
P4
le autofunzioni nel sottospazio generato da
n=0 cn | n i, essendo | n i gli autostati
dell’oscillatore armonico.
11.19) Il principio di Heisenberg afferma che una particella confinata in un recipiente di
volume finito non può avere energia cinetica zero. Spiegare perchè, e valutare la pressione
esercitata dalla particella nello stato fondamentale.
11.20) Dati tre operatori hermitiani N-dimensionali A, B e C , soddisfacenti le regole
di commutazione: [A, C] = [B, C] = 0 , [A, B] 6= 0 , dire se può esistere una base nella
quale l’operatore C ammette la rappresentazione: Cik = δik k con k = 1, 2, ..., N .
11.21) Una particella immersa nel potenziale U (x) si trova in uno stato stazionario.
Mostrare che la forza media che si esercita su di essa è nulla, cioè che F = −dU/dx ha
valore di aspettazione nullo sugli stati stazionari.
72
11. ARGOMENTI VARI. PROBLEMI.
11.22) Sia data una particella quantistica in un solo
grado di libertà soggetta a un potenziale
(
−V0 |x| < a
V =
0
a < |x| ,
−a
a
con V0 e a costanti reali positive. Se la particella
si trova inizialmente nello stato rappresentato da un
pacchetto d’onde gaussiano
ψ(x, t = 0) = A exp[−
−V
0
(x − x0 )2
− ik0 x]
4σ
con A, k0 , x0 e σ costanti reali positive, valutare la probabilità che a t > 0 l’energia
sia quella dello stato fondamentale. Si approssimino le formule ottenute nel caso in cui
x0 a . La probabilità richiesta dipende dal tempo t > 0 a cui si effettua la misura?
11.23) Una particella senza spin è immersa in un potenziale V (x) , e ha spettro puramente
discreto. Sfruttando il doppio commutatore [ [ H, exp{ix · k} ] , exp{−ix · k} ] , calcolare:
P
S = m (Wn − Wm ) | h n | exp{ix · k} | m i|2 ,
essendo k un vettore costante e Wn gli autovalori di H .
11.24) Un fascio di elettroni monocromatici passa
attraverso due fenditure distanti 2a = 1mm , formando
frange di interferenza su uno schermo posto a distanza
L = 1m . La distanza fra le frange nella regione
centrale è di d = 0.15 µ . Qual’è l’ordine di grandezza
dell’energia degli elettroni?
d
2a
L
11.25) Un rotatore piano di momento di inerzia I e momento di dipolo elettrico dE è
immerso in un debole campo elettrico omogeneo E0 diretto lungo il piano del rotatore.
Valutare la prima correzione non nulla all’energia. In questa approssimazione valutare la
polarizzabilità pE = ∂hdE i/∂E0 del rotatore nello stato.
11.26) Stimare le dimensioni dell’atomo a Z 1 elettroni, con il modello di Bohr, il
principio di esclusione di Pauli senza repulsione coulombiana, e nell’ipotesi di livelli pieni.
11.27) Un oscillatore armonico di carica q si trova nello stato fondamentale. A un certo
istante si accende un campo elettrico uniforme diretto lungo il semiasse positivo della
coordinata x. Determinare la probabilità di transizione verso gli stati eccitati del nuovo
sistema. [Vedi 3.4). Utilizzare la forma differenziale dei polinomi di Hermite.]
11. ARGOMENTI VARI. PROBLEMI.
73
11.28) La fisica di bassa energia di un sistema quantistico è descritto dalla matrice
−W0
0
0 0
−W0 ,
H = W0 0 0
0 W0 con reale. i) Dimostrare attraverso un calcolo esplicito che, qualunque sia il valore di
, gli autovalori di H si presentano sempre a coppie di valori, opposti in segno, cioè
W1 = −W3 , W2 = −W4 . Stabilire se questo è vero anche in generale per una qualunque
−W0 1
V , dove 1 è la matrice unità di dimensione n , e
matrice del tipo H = V † W 0 1
V è una matrice n−dimensionale arbitraria.
11.29) La funzione d’onda di una particella immersa in una buca di potenziale di profondità infinita e larghezza a (0 < x < a), è data da: 1) φ1 (x) = N1 x(x − a) ,
2) φ2 (x) = N2 sin2 (πx/a) . Calcolare le distribuzioni di probabilità dell’energia, valutando
numericamente i primi due coefficienti non nulli. Valutare inoltre il valor medio dell’energia
P
P∞
−2
−4
e il suo scarto quadratico medio. [ ∞
= π 2 /8 ,
= π 4 /96 .]
k=0 (2k + 1)
k=0 (2k + 1)
11.30) A due osservabili α e β corrispondono gli operatori A e B , con due autovalori
distinti non degeneri ciascuno, {a1 , a2 } e {b1 , b2 } , e due autovettori { | a1 i , | a2 i}
e { | b1 i , | b2 i} , rispettivamente. Valgono le relazioni | a1 i = c1 | b1 i + c2 | b2 i e
√
√
| a2 i = c2 | b1 i − c1 | b2 i dove c1 = 2/ 13 e c2 = 3/ 13 . i) Dire se α e β sono
compatibili, ovvero se i corrispondenti operatori commutano. ii) Se si misura α ottenendo
il valore a1 e immediatamente dopo si esegue una misura di β seguita da un’ulteriore
misura di α , dire qual’è la probabilità di ottenere ancora a1 per quest’ultima misura.
11.31) La funzione φ0 = N (x2 + a2 )−1 è autofunzione, con’autovalore zero, di:
1 d2
3x2 − a2
+
2 dx2 (x2 + a2 )2
Dimostrare che non esistono stati a energia negativa. [Si può procedere in vari modi: ad es.
dimostrando che H = D † D per qualche operatore D da determinare; oppure tenendo
presente una proprietà degli zeri delle autofunzioni dell’equazione di Schrödinger.]
H=−
11.32) Determinare lo spettro di una particella monodimensionale in un potenziale di ampiezza 2b e profondità V0 : V = −V0 θ(b − |x|) nel limite in cui V0 → ∞ , b → 0 ,
con 2V0 b = λ fissato. Se la particella si trova inizialmente nello stato rappresentato da
un pacchetto d’onde gaussiano: ψ0 = ψ(x; t = 0) = A exp [−(x − x0 )2 /4σ + ik0 x] , con
A, k0 , x0 e σ costanti reali positive, e 4σ ~2 /µλ , valutare la probabilità che un misura
dell’energia all’istante t > 0 dia come risultato l’energia del primo stato legato.
74
11. ARGOMENTI VARI. PROBLEMI.
11.33) Un atomo di Trizio (Z = 1, A = 3) si trova nel suo stato fondamentale. A un
certo istante nel nucleo avviene un decadimento radioattivo con emissione di un elettrone
e formazione di un nucleo di Elio. La transizione avviene in un tempo molto breve sulla
scala dei tempi atomici. Trovare le probabilità che lo ione di Elio He+ si trovi nello stato
fondamentale, nello stato eccitato 2s , o in quello 2p .
11.34) Un sistema quantomeccanico possiede solo due autostati dell’energia, | 1 i e | 2 i .
Si conoscono altre tre osservabili, oltre l’energia, A , B , C . Gli stati | 1 i e | 2 i
sono normalizzati e non sono necessariamente autostati di A , B , C . Determinare gli
autostati e gli autovalori di A , B , C , a partire dai tre seguenti “risultati sperimentali”,
sapendo però che uno di questi è sbagliato:
i) h 1 | A | 1 i = 1/2 , h 1 | A2 | 1 i = 1/4 ; ii) h 1 | B | 1 i = 1/2 , h 1 | B 2 | 1 i = 1/6 ;
iii) h 1 | C | 1 i = 1 , h 1 | C 2 | 1 i = 5/4 , h 1 | C 3 | 1 i = 7/4 .
11.35) Si consideri una particella di massa µ , soggetta a un potenziale di tipo buca infinita,
con 0 < x < a . La funzione d’onda iniziale è data da
ψ(x; t = 0) = N [ 1 − cos(2πx/a) ]
essendo N una costante di normalizzazione. Si calcoli il valore medio dell’energia della
particella a un tempo t qualunque. Qual’è la probabilità di misurare un’energia pari a
quella dello stato fondamentale e a quella del primo stato eccitato?
11.36) Per un atomo a Z elettroni, valutare il raggio medio in funzione di Z , nel modello
a shells piene e nei due casi tipici, metalli alcalini o schermaggio parziale. (Vedi 11.26).)
11.37) Una particella monodimensionale di massa µ è confinata in una scatola di larghezza
a = 10−10 m , e si trova nel suo stato fondamentale con energia pari a 38 eV . Quale forza
esercita sulle pareti della scatola? Quale sarà la sua energia nel primo stato eccitato?
11.38) Un sistema quantistico finito dimensionale è soggetto all’Hamiltoniana:
H = H0 + W 1 A + A
†
= W0
N
X
n=1
| n ih n | + W1
N
X
n=1
( | n ih n + 1 | + | n + 1 ih n | )
con | N + 1 i = | 1 i . Dimostrare che AA† = A† A = I . Dimostrare inoltre che
[H0 , A] = [H0 , A† ] = 0 . Valutare autovalori e autofunzioni dell’Hamiltoniana totale.
11.39) Un oscillatore armonico si trova nello stato fondamentale. Quale è la probabilità di
trovarlo all’esterno della regione classica? Dare la stima numerica, utilizzando i valori della
funzione d’errore (vedi A-S 7.).
11. ARGOMENTI VARI. PROBLEMI.
75
11.40) Dato un oscillatore lineare armonico e dette ψ0 e ψ1 le autofunzioni reali normalizzate relative allo stato fondamentale e al primo stato eccitato. Sia φ = aψ 0 + bψ1
la funzione d’onda dell’oscillatore a un certo istante. i) Mostrare che il valor medio di x
è in generale diverso da zero. ii) Quali valori di a rendono massimo h x iφ , e quali lo
rendono minimo?
11.41) Una particella monodimensionale si trova inizialmente nello stato fondamentale di
una buca quadrata infinita con 0 ≤ x ≤ a . Improvvisamente (!) la parete destra della
buca viene spostata in x = 2a . a) Calcolare la probabilità che la particella possa venire
trovata nello stato fondamentale della buca espansa. b) Trovare lo stato della buca espansa
che ha maggior probabilità di essere occupato.
Supponiamo invece che la buca originale con 0 ≤ x ≤ a improvvisamente (!) si dissolva.
c) Se, come prima, la particella si trova nello stato fondamentale, quale sarà la distribuzione
di probabilità del momento della particella liberata?
11.42) Consideriamo la funzione d’onda monodimensionale ψ(x) = N (x/x0 )j e−x/xo , con
N , j , x0 costanti positive, con j = 1, 2, 3, ... a) Usando l’equazione di Schrödinger,
trovare il potenziale V (x) e l’energia W per i quali questa funzione d’onda è un’autofunzione, nell’ipotesi che V (x) → 0 per x → ∞ . b) Illustrare la differenza tra il potenziale
trovato e quello radiale efficace per uno stato idrogenoide di momento angolare l .
11.43) Una particella monodimensionale di massa µ è immersa in un potenziale V (x) ,
e la sua funzione d’onda è data da: ψ(x; t) = N x exp[−αx + iβt/~] per x > 0 , e zero
altrove, con N , α , β costanti positive. a) La particella è legata? Perchè ? b) Trovare il
potenziale V (x) e valutare il suo spettro. c) Per lo stato assegnato, valutare le probabilità
relative all’energia.
11.44) Sia dato un oscillatore armonico di massa µ e frequenza ω nello stato iniziale:
√ P +s
ψ(0) = 1/ 2s N
N s 1 , mostrare che il valore di
n=N −s | n i . i) Nel caso
aspettazione dell’osservabile x ha comportamento sinusoidale nel tempo con ampiezza
p
2~N/µω . ii) Confrontare con il comportamento dell’oscillatore classico di pari energia.
11.45) La parte angolare della funzione d’onda di una particella tridimensionale è data da:
ψ = A exp[2iϕ] . Qual’è la probabilità di trovare il valore l in una misura del momento
angolare totale? [ Suggerimento. Utilizzare le relazioni: (1 − ζ 2 )Pl00 = 2 ζPl0 − l(l + 1)Pl ,
e Pl (1) = (−)l Pl (−1) = 1 , dove i Pl (ζ) sono i polinomi ortogonali di Legendre.]
p
√
h
2
2
i
11.46) La funzione ψ(x) = a/ π exp −a /2 (x−x0 ) descrive lo stato di una particella
monodimensionale. a) Controllare che la funzione sia correttamente normalizzata.
76
11. ARGOMENTI VARI. PROBLEMI.
b) Valutare la probabilità che il momento lineare sia compreso tra p e p + dp . c) Valutare
per questa il principio di indeterminazione, cioè il valore del prodotto ∆x ∆p tra le radici
quadrate degli scarti quadratici di posizione e momento.