Circuito LC
Un condensatore di capacità C, inizialmente carico e un induttore L connessi in serie. L’equazione del
circuito può essere ricavata in due modi. Dal punto di vista della legge di Kirchhoff (delle maglie), la
d.d.p. ai capi del condensatore vale VC = q / C mentre la d.d.p. ai capi dell’induttanza vale V L = - L di /
dt. Non essendoci generatori, la legge di Kirchhoff si può scrivere:
di q
d2 q
q
0 cioè
– VC – VL = 0 cioè L
0 Dal punto di vista energetico, invece,
dt C
dt 2 L C
1 2 1 q2
Li
cost
L’energia totale del circuito è costante e pari a U = UC + UL cioè, sostituendo: U
2
2
C
di q dq
d 2q q
0 Li
0 L 2
Derivando :
dt C dt
dt
C
Un’equazione di questo tipo è analoga a quella del moto armonico oscillante e può essere scritta come:
d2 q
1
2
0 la cui soluzione è q Q cos t
è chiamata frequenza
0 q
2
dt
LC
dq
i
Q
sin
t
I sin t
caratteristica del circuito. La corrente è
dt
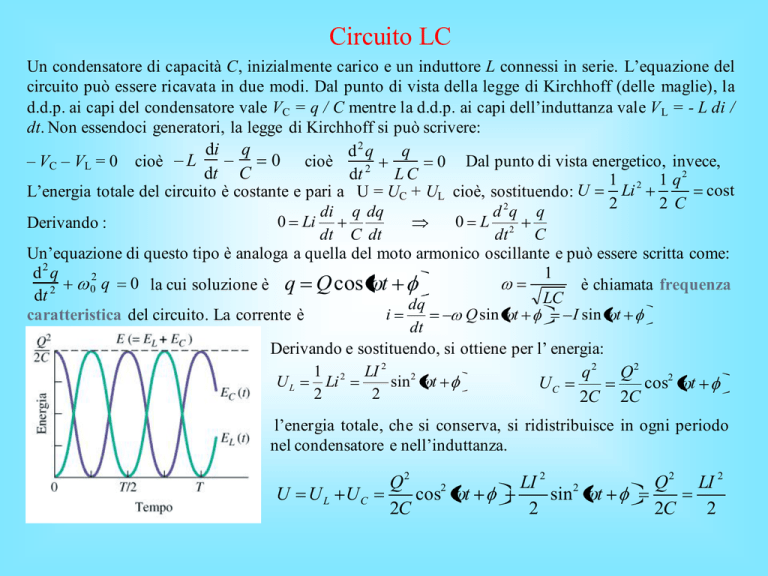
Derivando e sostituendo, si ottiene per l’ energia:
1 2 LI 2
q 2 Q2
2
UL
Li
sin t
UC
cos2 t
2
2
2C 2C
l’energia totale, che si conserva, si ridistribuisce in ogni periodo
nel condensatore e nell’induttanza.
U U L UC
Q2
cos2 t
2C
LI 2 2
sin t
2
Q2
2C
LI 2
2
q
Carica, corrente, energia nel circuito LC
i
Q
I
t
t
(a) Condensatore completamente
carico, i=0
(b) Condensatore in scarica, i aumenta
(c) Condensatore completamente
scarico, i=imax
(d) Condensatore in carica, i
diminuisce
(e) Condensatore completamente
carico ma con polarità opposta
rispetto ad (a), i=0
(f) Condensatore in scarica, i aumenta
ma nel verso opposto rispetto a (b)
(g) Condensatore completamente
scarico, i=imax
(h) Condensatore in carica, i
diminuisce
LC - analogia meccanica
L’equazione del circuito LC è formalmente uguale a quella dell’oscillatore armonico
d 2x
m 2 kx 0
dt
=0
in presenza di una E (f.e.m.) costante la
frequenza è la stessa ma Q oscilla intorno a
Q eq=EC. Per la molla-peso in verticale la
posizione di equilibrio trasla di x=mg/k
La corrente alternata
una spira rotante con velocità angolare costante di sezione
A immersa nel campo magnetico B. L’angolo
tra la
direzione del campo magnetico e la normale alla spira (che è
anche la direzione del momento magnetico ) varia nel
tempo come: = t per cui il flusso del campo magnetico
attraverso la spira vale:
A B cos
B
A B cos
t
la f.e.m. originata dalla variazione temporale del flusso del
campo magnetico è:
E=
d
B
dt
AB
sin
i
t
Nel caso di una bobina con N spire, si ha:
E=
R
E(
d B
N
dt
NAB
sin
t
se il circuito è connesso a un utilizzatore con carico R, la
corrente e la potenza possono essere espresse come:
i
E
i
E
R
NAB
R
E0
sin
I
t
t
pt
Ei
E0 I sin
2
p
E0 I
t
t
t
circuito resistivo in alternata
per la legge di Kirchhoff
E – vR = 0
dove la tensione alternata forzante del circuito vale
E = Em sin gt
il che porta a scrivere ovviamente
vR = Em sin gt
che può essere scritto come
vR = VR sin gt con VR = Em.
La corrente che fluisce nel circuito, per definizione di resistenza, vale:
iR = IR sin gt con VR = IR R
Questa equazione stabilisce che, in un circuito puramente resistivo, la
corrente ha la stessa fase della tensione applicata.
Le grandezze variabili tensione vR e corrente i R possono essere rappresentate
graficamente con il metodo dei fasori (vettore di fase rotante attorno
all’origine).
L’angolo di rotazione rispetto all’asse x fornisce un’indicazione della fase
( gt). La lunghezza del fasore rappresenta l’ampiezza (V R o IR), mentre la
sua proiezione sull’asse verticale rappresenta il valore della grandezza al
tempo t.
In questo caso i due vettori tensione e corrente sono sovrapposti.
circuito capacitivo in alternata
legge di Kirchhoff
E – vC = 0
dove
E = Em sin
gt
il che porta a scrivere
vC = VC sin gt con VC = Em.
la carica sulle armature del condensatore, è:
qC = C vC = C VC sin gt
la corrente nel circuito è la derivata di qC, cioè:
iC = dqC / dt = g C V C cos gt = VC / X C sin (
con
XC
1
gC
ed anche
gt
+ 90 )
VC = XC IC
dove XC è chiamata reattanza capacitiva del condensatore.
la reattanza capacitiva, grandezza che ha le dimensioni di una resistenza,
dipende non soltanto da C ma anche da .
in un circuito puramente capacitivo, la corrente e la tensione sono sfasate di
90 . In particolare, la corrente è in anticipo di fase di un quarto di
periodo.
il fasore della corrente è spostato di 90 verso sinistra (in anticipo) rispetto al
fasore della tensione.
circuito induttivo in alternata
legge di Kirchhoff
E – vL = 0
E = Em sin
dove
gt
vL = VL sin gt con VL = Em.
a tensione ai capi di un’induttanza è data dalla legge di Lenz:
vL
L
diL
dt
E combinando tali equazioni si ottiene:
diL
dt
VL
sin
L
gt
iL
diL
VL
sin
L
g tdt
VL
cos
gL
g
t
+costante (=0)
indicando la reattanza induttiva con:
XL = g L
si ha
e la corrente può essere espressa come:
iL = VL / X L sin (
VL = XL IL
gt
- 90 )
la reattanza induttiva ha le dimensioni di una resistenza e dipende non
soltanto da L ma anche da .
in un circuito puramente induttivo, la corrente e la tensione sono sfasate di
90 . In particolare, la corrente è in ritardo di fase di un quarto di periodo.
RLC serie in alternata
un circuito RLC serie forzato da una tensione alternata (sinusoidale)
E = Em sin gt ; i = I sin ( gt - )
si ha:
Em2 = VR2 + (VL - VC )2
Em2 = (I R)2 + (I XL - I XC )2
e, sostituendo i valori delle ampiezze delle d.d.p., si ottiene
Em
cioè: I
R
2
XL
XC
2
Em
dove
Z
Z
R2
XL
VL VC
VR
XL
XC
Per l’angolo di sfasamento si ha:
tg
XC
R
è chiamata impedenza.
Sfasamenti e risonanza
A seconda dei valori delle reattanze si hanno alcuni casi particolari.
Se X L > XC il circuito è prevalentemente induttivo la corrente è in
ritardo di fase rispetto alla tensione
Se XC > X L il circuito è prevalentemente capacitivo la corrente è
in anticipo di fase rispetto alla tensione
Se XL = XC il circuito è detto in risonanza e =0. In queste
condizioni è come se L e C non ci fossero ed inoltre si ha:
g
1
LC
transitorio RLC all’oscilloscopio
Metodo simbolico per i circuiti in corrente alternata
L’impedenza totale di un generico circuito ha sempre una parte reale
Zr, e una parte immaginaria Zi che viene chiamata reattanza e
indicata con la lettera X :
X
Z Z 0ei
Z r iX
,
Z0
Z r2 X 2
,
tg
.
Zr
Analogamente per l’ammettenza dello stesso circuito si scrive:
Y
Y0 e
i
G iB
,
Y0
G
2
B
2
,
tg
B
G
dove la parte reale G è detta conduttanza e la parte immaginaria B è
detta suscettanza.
,
http://www.ngsir.netfirms.com/englishhtm/RLC.htm
Identità di Eulero
Formula di Eulero
fasore un numero complesso,
rappresentabile come vettore nel
piano complesso. Con il metodo
simbolico rappresenta, in campo
complesso, tensione o corrente
alternata.












