Test di fisica sui circuiti – Classe 5E – 3 dicembre

Test di fisica sui circuiti
– Classe 5E – 3 dicembre 2015
Durata: 55 minuti. Soglia sufficienza: 60 pt. Punteggio massimo: 100 pt.
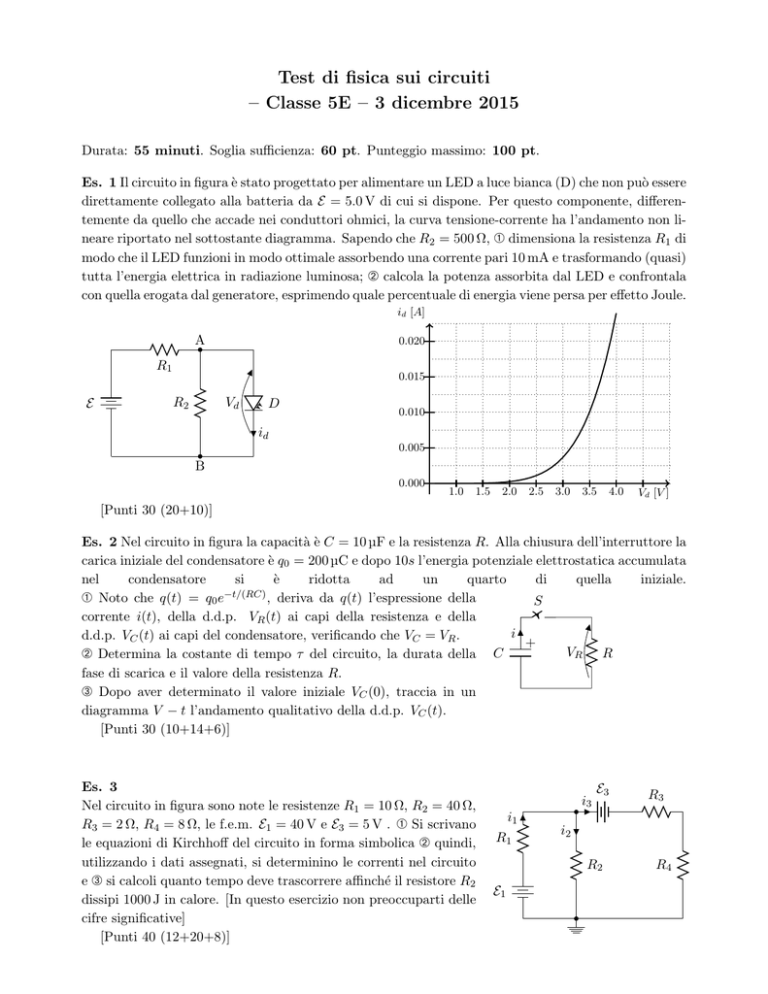
Es. 1 Il circuito in figura è stato progettato per alimentare un LED a luce bianca (D) che non può essere
direttamente collegato alla batteria da E = 5.0 V di cui si dispone. Per questo componente, differentemente da quello che accade nei conduttori ohmici, la curva tensione-corrente ha l’andamento non lineare riportato nel sottostante diagramma. Sapendo che R2 = 500 Ω, À dimensiona la resistenza R1 di
modo che il LED funzioni in modo ottimale assorbendo una corrente pari 10 mA e trasformando (quasi)
tutta l’energia elettrica in radiazione luminosa; Á calcola la potenza assorbita dal LED e confrontala
con quella erogata dal generatore, esprimendo quale percentuale di energia viene persa per effetto Joule.
id [A]
A
0.020
R1
E
0.015
Vd
R2
D
0.010
id
0.005
B
0.000
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Vd [V ]
[Punti 30 (20+10)]
Es. 2 Nel circuito in figura la capacità è C = 10 µF e la resistenza R. Alla chiusura dell’interruttore la
carica iniziale del condensatore è q0 = 200 µC e dopo 10s l’energia potenziale elettrostatica accumulata
nel
condensatore
si
è
ridotta
ad
un
quarto
di
quella
iniziale.
−t/(RC)
À Noto che q(t) = q0 e
, deriva da q(t) l’espressione della
S
corrente i(t), della d.d.p. VR (t) ai capi della resistenza e della
i
d.d.p. VC (t) ai capi del condensatore, verificando che VC = VR .
+
VR R
Á Determina la costante di tempo τ del circuito, la durata della C
fase di scarica e il valore della resistenza R.
 Dopo aver determinato il valore iniziale VC (0), traccia in un
diagramma V − t l’andamento qualitativo della d.d.p. VC (t).
[Punti 30 (10+14+6)]
Es. 3
Nel circuito in figura sono note le resistenze R1 = 10 Ω, R2 = 40 Ω,
R3 = 2 Ω, R4 = 8 Ω, le f.e.m. E1 = 40 V e E3 = 5 V . À Si scrivano
le equazioni di Kirchhoff del circuito in forma simbolica Á quindi,
utilizzando i dati assegnati, si determinino le correnti nel circuito
e  si calcoli quanto tempo deve trascorrere affinché il resistore R2
dissipi 1000 J in calore. [In questo esercizio non preoccuparti delle
cifre significative]
[Punti 40 (12+20+8)]
i3
i1
R1
E3
i2
R2
E1
R3
R4