s_040217

STATISTICA E MISURAZIONE
martedì 17 febbraio 2004
Prof. Cesare Svelto
Primo appello AA 2003/2004
Tempo a disposizione 2 ore e 45 min (1 ora e 30 min metà prova)
Aula Vs.8 ore 9.15
Cognome: __________________________
nome: _____________________
Matricola e firma __ __ __ __ __ __
(stampatello)
_____________________ (firma leggibile)
Esercizi svolti (almeno parzialmente): 1 2 3 4 5
(crocettare)
N.B. gli esercizi non crocettati non saranno corretti; quelli crocettati ma neanche iniziati comporteranno una
penalità.
Crocettare:
SOLO PRIMA PARTE (1a 2 3)  SOLO SECONDA PARTE(1bcd 4 5) 
ESAME INTERO 
PUNTEGGI: (10+11+11=32 p)
(11+10+11=32 p)
(9+6+6+6+6=33 p)
SOLUZIONI
Esercizio 1
(svolgere su questo foglio e sul retro)
1) Siamo incaricati di effettuare un controllo statistico su una ditta che imbottiglia acque minerali. Si vuole
controllare l’esatto livello medio di acqua presente in ogni bottiglia, dichiarato 1.5 l dalla ditta. È noto che le
macchine imbottigliatrici hanno una deviazione standard  = 10 ml. Prendiamo quindi due casse da 6
bottiglie e ne misuriamo il contenuto, ottenendo i seguenti valori:
Litri di acqua: 1.493, 1.503, 1.500, 1.483, 1.479, 1.496, 1.467, 1.501, 1.495, 1.502, 1.475, 1.486.
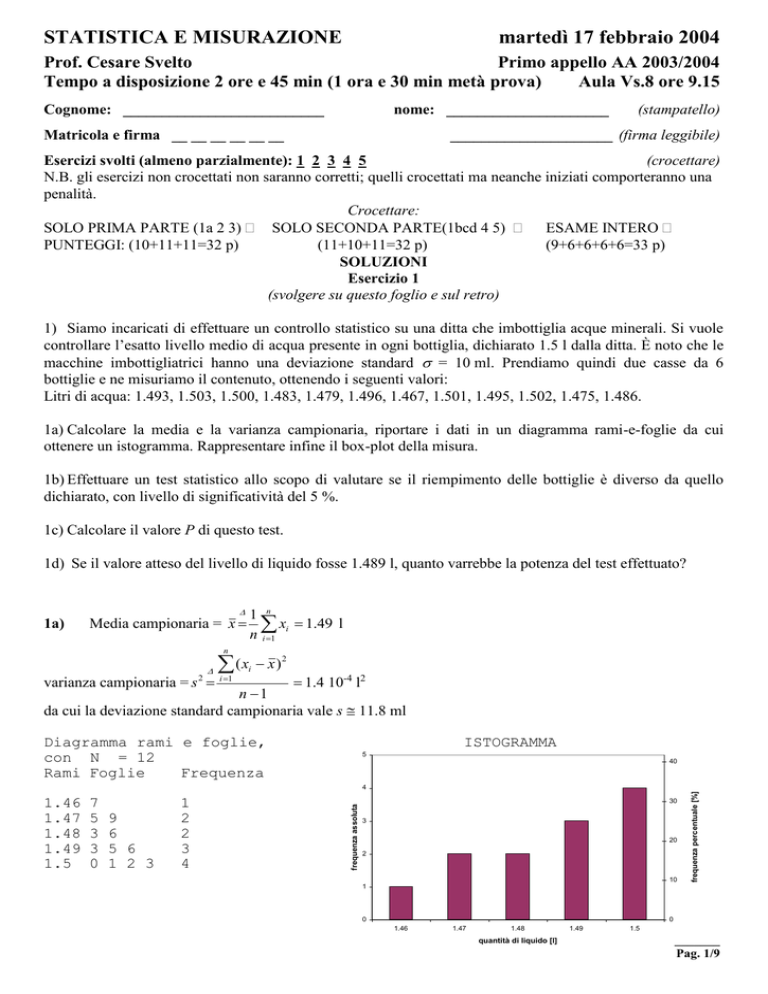
1a) Calcolare la media e la varianza campionaria, riportare i dati in un diagramma rami-e-foglie da cui
ottenere un istogramma. Rappresentare infine il box-plot della misura.
1b) Effettuare un test statistico allo scopo di valutare se il riempimento delle bottiglie è diverso da quello
dichiarato, con livello di significatività del 5 %.
1c) Calcolare il valore P di questo test.
1d) Se il valore atteso del livello di liquido fosse 1.489 l, quanto varrebbe la potenza del test effettuato?

1a)
Media campionaria = x 
1 n
 xi  1.49 l
n i 1
n

varianza campionaria = s 2 
(x  x)
2
i
 1.4 10-4 l2
n 1
da cui la deviazione standard campionaria vale s  11.8 ml
i 1
Diagramma rami e foglie,
con N = 12
Rami Foglie
Frequenza
ISTOGRAMMA
5
40
9
6
5 6
1 2 3
1
2
2
3
4
30
3
20
2
10
frequenza percentuale [%]
7
5
3
3
0
frequenza assoluta
4
1.46
1.47
1.48
1.49
1.5
1
0
0
1.46
1.47
1.48
quantità di liquido [l]
1.49
1.5
_______
Pag. 1/9
Esercizio 1 (continua)
BOX PLOT:
minimo= 1.467 l
primo quartile= 1.480 l
mediana= 1.494 l
terzo quartile= 1.5075 l
massimo=1.503 l
I baffi comprendono tutti i punti rimanenti, in quanto tutti i valori misurati sonocontenuti all’interno di 1.5
volte la dinamica interquartile.
1b) Dato che la varianza è nota, si può effettuare un test Z. Seguiamo gli 8 passi descritti nel libro di testo.
1. Il parametro di interesse è la quantità attesa di liquido 
2. H0:  = 1.5 l
3. H1:   1.5 l (il test è a due lati, in quanto espressamente richiesto dal testo: si vuole rivelare una
qualsiasi differenza)
4. livello di significatività richiesto  = 0.05
5. La statistica di test è la statistica Z: z0 
X 
X

X 
/ n
6. Rifiutiamo H0 se z0 > Z/2 = 1.96 oppure z0 < -Z/2 = -1.96 (questi valori si ricavano dalla tabella della
funzione cumulativa per una VNS in corrispondenza di un valore di probabilità /2=0.025)
7. Calcoliamo quindi z0, z0 
X 
X

X   1.49  1.5

 3.46
 / n 0.01 / 12
8. Conclusione: dato che z0 = -3.46 < -Z/2 = -1.96 possiamo rifiutare l’ipotesi nulla con livello di
significatività 0.05: c’è abbastanza evidenza che l’ipotesi nulla sia falsa.
Concludiamo che il livello di riempimento delle bottiglie è significativamente diverso da 1.5 l.
1c) Il valore P, che corrisponde al livello di significatività di soglia tra l’accettazione ed il rifiuto di H0, si
può ricavare direttamente dalla tabella dei valori della funzione cumulativa:
ZP/2 = z0 = 3.46, per cui il valore P =20.00027=0.00054.
L’interpretazione di questo valore è che l’ipotesi nulla è dichiarata falsa per qualsiasi livello di significatività
 maggiore dello 0.054 %. In questo caso, infatti, con  = 5 % abbiamo rifiutato H0.
1d) La potenza di un test statistico è la probabilità di rifiutare l’ipotesi nulla quando questa è falsa. È uguale
a 1- la probabilità  di errore di tipo II:
Potenza = 1 -  = 1 - P(errore di tipo II) = 1 - P(accettare H0 quando H0 è falsa)
 = probabilità che la media campionaria entri nella regione di accettazione, sapendo che il valore atteso della
popolazione è 1.489 l.
La regione di accettazione va calcolata a partire da  (prima l’abbiamo calcolata per la variabile
standardizzata):
X up  0  Z / 2   x  0  Z / 2   / n  1.5  1.96  0.01/ 12  1.5057 l
X down  0  Z / 2   x  0  Z / 2   / n  1.5  1.96  0.01/ 12  1.4943 l
(difatti prima abbiamo rifiutato l’ipotesi nulla, perché 1.49 l è al di fuori della regione di accettazione).
Continua all’ultimo foglio.......................
_______
Pag. 2/9
Esercizio 2
(svolgere su questo foglio e sul retro)
2) Si consideri il dado in figura.
2a) Quanto vale la probabilità che su venti lanci esca croce esattamente 9 volte?
2b) Quanto vale invece la probabilità che, su 10 lanci, si abbia almeno per tre volte testa?
Jolly
2c) Sapendo che la quantità di pacchi ricevuti da un magazzino segue una statistica poissoniana con valor
medio di 12 pacchi all’ora, quanto vale la probabilità che in 2 ore vengano ricevuti esattamente 20 pacchi?
2d) Supponendo che l’addetto si assenti per 10 minuti, quanto vale invece la probabilità che in quel tempo
non arrivi neanche un pacco?
2a) Dato che ogni prova è un processo di Bernoulli (o esce o non esce croce), le 20 prove sono indipendenti e
la probabilità di successo in ogni prova è costante p =2/6=0.333, la probabilità di x volte testa su n estrazioni
segue la distribuzione binomiale:
 n
 20 
P(9 successi su 20 prove )    p x (1  p)n x   0.3339 (0.667)20 9  0.099  10 %
 x
9
n
n!
ricordando che   
 x  x!(n  x)!
2b) La probabilità di avere testa su una singola estrazione è p = 3/6=0.5.
P(almeno 3 volte testa) = 1 – P(2 volte testa) – P(1 volta testa) – P(mai testa) =
10 
10 
2
1
=1-  0.5 (0.5)102   0.5 (0.5)101  (0.5)10  94.5 %
2
1
2c) La funzione di probabilità di una variabile poissoniana X vale f ( x) 
Il valor medio di pacchi in 2 ore vale  = 12 pacchi/h ∙ 2 h = 24 pacchi.
La probabilità che in 2 ore arrivino esattamente 20 pacchi è pari a
e  20 e 24 2420
P( x  20) 

 0.0624  6.24 %
20!
20!
e   x
,
x!
x  0,1,2...
2d) Il valor medio di pacchi in 10 minuti vale  = 12 pacchi/h ∙ 1/6 h = 2 pacchi.
La probabilità che arrivino esattamente 0 pacchi in 10 minuti è pari a
e  0 e 2
P( x  0) 

 0.1353  13.53 %
0!
1
_______
Pag. 3/9
Esercizio 3
(svolgere su questo foglio e sul retro)
3a) Descrivere le proprietà della distribuzione di probabilità normale, indicando i motivi della sua
importanza. Si riporti prima l’espressione analitica di questa distribuzione e se ne descrivano i parametri
caratteristici.
3b) Una ditta di elettrodomestici produce un frullatore che emette in prossimità un campo elettrico di 4 V/m,
con deviazione standard di 0.8 V/m (dovuta alla variabilità della produzione). Sapendo che la normativa
vigente impone un limite massimo pari a 6 V/m, che percentuale di elettrodomestici verrà scartata in quanto
fuori norma?
3a) Una variabile casuale X con funzione di densità di probabilità
p ( x)  f  x   g  x  
 x- 2 
1
per - < x <+ ha una distribuzione normale, o gaussiana, ed è
exp 
2 
2π σ
 2 
chiamata variabile casuale normale, con parametri  (media) e  (deviazione standard), dove - <  <+ e 
>0. Inoltre
E(X) =  e V(X)=  2.
La distribuzione è unimodale e simmetrica e dunque la media  coincide anche con la moda (valore più
probabile) e la mediana (50° percentile). La deviazione standard  indica, al solito, la “larghezza della curva”
e in questo caso l’intervallo di valori compresi tra - e + corrisponde a una probabilità del 68.7 % circa.
Il principale motivo dell’importanza della distribuzione normale è la sua applicabilità a moltissimi casi reali:
tutti i processi che sono determinati da diverse cause indipendenti (e non deterministiche) tendono ad avere
una distribuzione di probabilità gaussiana (si pensi al teorema del limite centrale: il valor medio di una
qualsiasi popolazione tende ad avere una distribuzione normale, indipendentemente dalla distribuzione di
probabilità di origine).
3b) Il problema si riduce al calcolo della probabilità di oltrepassare la soglia della normativa (campo elettrico
E > 6 V/m).
Per calcolare la probabilità standardizziamo la variabile casuale gaussiana, sapendo che  = 4 V/m e
 = 0.8 V/m, ricorriamo quindi alla tabella dei valori della distribuzione cumulativa normale standard
6
64


P( E  6 V/m )  P z 
  P z 
  P( z  2.5)  1  P( z  2.5)  1  Φ(2.5)  1  0.9938  0.62 %
 
0.8 


_______
Pag. 4/9
Esercizio 4
(svolgere su questo foglio e sul retro)
4a) Si spieghi perché uno strumento che esegue misure quantizzate presenta una incertezza intrinseca. A
quale categoria appartiene questa incertezza?
4b) Si dimostri, mostrando tutti i passaggi svolti, che uno strumento con misura uniformemente quantizzata
presenta una incertezza intrinseca direttamente proporzionale alla larghezza dell’intervallo di quantizzazione.
Per la dimostrazione si consideri un intervallo di quantizzazione uniforme tra i valori a (estremo inferiore) e b
(estremo superiore), come mostrato in figura. N.B. Si ricavi la varianza della misura; la sua incertezza tipo.
a
b
x
4c) Si ricavi il valore atteso per una misura che cade nell’intervallo.
4d) Un uomo di massa 78,115 kg (nota con incertezza trascurabile) sale su una bilancia elettronica digitale
con portata 150,0 kg e risoluzione 100 g. Si indichi la misura dello strumento (ideale) e la sua incertezza
standard. Quali altri errori potrebbero portare, per uno strumento reale, a una diversa lettura e/o a una
maggiore incertezza di misura?
4a) Lo strumento con misura quantizzata presenta una incertezza intrinseca in quanto a un’intera fascia di
valori del misurando lo strumento associa un unico valore numerico misurato. Pertanto il valore di misura è
rappresentativo di un intervallo di valori, per ipotesi con densità di probabilità (PDF) di tipo uniforme, e la
sua media e la deviazione standard (incertezza tipo) si possono calcolare mediante analisi statistica su una
PDF assunta a priori (incertezza di categoria B). Questa incertezza viene solitamente chiamata incertezza di
quantizzazione ed è intrinseca a tutti i fenomeni e misure che riportano su una scala di valori discreti una
grandezza originariamente continua.
4b) È noto che un intervallo di quantizzazione uniforme di larghezza x=(b-a) ha valore centrale (medio)
(x)=(b+a)/2 e varianza 2(x)=(x)2/12 da cui una deviazione standard o incertezza tipo (x)=u(x)=x/ 12 .
Per dimostrare questi risultati, cominciamo riportando la funzione analitica che descrive la PDF uniforme
nell’intervallo [a, b]:
 0
 1
px   
b  a
 0
xa
a xb
xb
Calcoliamo quindi la sua varianza:


2
UNI
b

x     x  b  a  px dx    x  b  a  1 dx 
2 
2  ba
a 
 
2
  x  b  a 
1 
2 

ba 
3

3




2
b
1

ba
1  b  a   a  b 
 


3  2   2 
3
3
2

1 1

b  a
3
2b  a  

12
 24 b  a
a
da cui l’incertezza tipo è appunto u(x)=(x)=
ba
12
e risulta direttamente proporzionale alla larghezza
dell’intervallo.
_______
Pag. 5/9
Esercizio 4 (continua)
4c) Il valore atteso della misura si calcola come:

b
1

 UNI x    xpx dx   x
dx 
a b  a

1  x2 

ba
 2 
b

a


1 1 2
ba
b  a2 
ba 2
2
4d) Il valore numerico letto dalla bilancia è di 78,1 kg. Il valore misurato dallo strumento digitale ideale è
m=78,100 kg0,029 kg, avendo ricavato l’incertezza tipo u(m)=m/ 12 =(100 g)/ 12 =29 g=0,029 kg e
avendo espresso il valore numerico di m con un numero di cifre significative proporzionate al livello di
incertezza della misura (quest’ultima espressa, come dalle raccomandazioni internazionali in materia, con 2
cifre significative: nel caso specifico, le decine e le unità di grammi).
_______
Pag. 6/9
Esercizio 5
(svolgere su questo foglio e sul retro)
5a) Si dia la definizione dei seguenti termini metrologici:
 Risoluzione
 Sensibilità
 Riproducibilità
5b) La formula che descrive la capacità di un condensatore in funzione delle sue dimensioni fisiche è la
seguente:
S
C   0  r , dove 0 ed r sono rispettivamente la costante dielettrica del vuoto e del materiale contenuto tra
d
le piastre del condensatore, S è l’area delle piastre e d la loro distanza. In un laboratorio vengono eseguite
misure di capacità di N=10 condensatori contenenti un determinato dielettrico (ossido di tantalio) del quale si
vuole determinare al costante dielettrica  r . La superficie S misura 15% mm2 (dato fornito dal costruttore),
mentre la distanza d è pari a 45 m (misurata con uno strumento a display digitale con risoluzione di 1 m).
La costante dielettrica del vuoto è  0 = 8.8542 10-12 F/m e la sua incertezza relativa dovrebbe essere nota a chi
abbia studiato i fondamenti di misurazione. Le 10 letture di capacità hanno fornito un valor medio pari a 5 pF
con deviazione standard campionaria di 0.40 pF.
Ricavate il valore di misura della costante dielettrica  r del materiale, la sua incertezza tipo u(  r ) e
l’incertezza relativa uR(  r ).
5a) Si vedano gli appunti e le dispense del corso
5b) Calcoliamo il valore atteso della misura:
Cd
1  1012  45  106
r 

 25.41 (si ricordi che  r è un numero puro).
S 0 1  10 6  8.8542  1012
Lo scarto tipo del valor medio (incertezza di categoria A) si ricava dalla deviazione standard campionaria
dividendola per la radice del numero di campioni:
u(C)=
sCi  400
fF=0.13 pF

N
10
L’incertezza relativa vale uR(C)=
u C  0.13

 2.6 % .
C
5
L’incertezza relativa della superficie S è data dal testo uR(S)=5 %, mentre  0 è esente da incertezza, in quanto
deriva direttamente dalla velocità della luce e dalla permeabilità magnetica, entrambe grandezze definite
senza incertezza.
_______
Pag. 7/9
Esercizio 5 (continua)
L’incertezza sulla misura dello spessore è dovuta alla quantizzazione dello strumento digitale ed è pari
all’ampiezza dell’intervallo divisa per
uR(d)=
12 : u(d)=
1
12
m= 0.29 m. Da cui un’incertezza relativa pari a
u d  0.29

 0.64 % .
d
45
Dato che la relazione funzionale che lega  r alle altre grandezze implica solo prodotti e divisioni con
esponenti unitari, è possibile ottenere direttamente l’incertezza relativa come somma quadratica delle
incertezze relative (si vedano le dispense del corso):
[ uR(r) ]2 = [ uR(S) ]2 + [ uR(d) ]2 +[ uR(C) ]2 = 0.052 + 0.00642+ 0.0262  3.2210-3
da cui uR(r) = 5.7 %
e u(r) = uR(r) r =1.4
La misura effettuata ha fornito quindi il seguente risultato: r = 25.4  1.4.
_______
Pag. 8/9
Esercizio _1_ (continua)
[foglio addizionale per eventuale esercizio “lungo”]
X up   

X

  P z  down






X
X






1.5057  1.489 
1.4943  1.489 
 P z 
  P z 
 
0.01 / 12 
0.01 / 12 


 Pz  5.785  Pz  1.836  1  0.967  3.3 %

  PX down  X  X up con   1.489  P z 
Per cui la potenza del test è
Potenza = 1 -  = 1-0.033=96.7 %
Questo significa che il test effettuato ha il 96.7 % di probabilità di rifiutare l’ipotesi nulla se il valore atteso
della popolazione vale 1.489 l.
_______
Pag. 9/9