esperienze

UNIVERSITA’ DEGLI STUDI DI LECCE
DIPARTIMENTO DI FISICA
ESPERIMENTAZIONI DI FISICA III
Foto di una bobina di Rogowski per la diagnostica di fasci di elettroni
ESPERIENZE
Limiti di misura dell’oscilloscopio
Circuito derivatore CR
Circuito integratore RC
Circuito Oscillante
Studio del campo elettro-magnetico prodotto
da una bobina
Caratteristica statica e dinamica di un diodo
Capacita’ della giunzione di un diodo
Raddrizzatore di tensione
Progetto di un Luxmetro con l’ausilio
dell’autocad
Raddrizzatore stabilizzato
Polarizzazione di un transistor ad emitter
comune
Amplificatore ad emettitore comune
Amplificatore a collettore comune
Amplificatore
ad
emettitore
comune
autopolarizzato
Oscillatore a sfasamento
Multivibratore astabile
Studio dei fenomeni di diffrazione
Studio dei fenomeni di interferenza
Monocromatore
Determinazione della costante di Planck ed
effetto fotoelettrico
V. Nassisi
1
Strumenti di misura
Operare in un laboratorio di fisica significa condurre delle esperienze e quantificare le
grandezze che le caratterizzano. Allora, i risultati possono essere dei semplici valori o leggi di
comportamento, ma in ogni caso si devono eseguire misure di: dimensioni, tempi, correnti
elettriche, tensioni, ecc. Per misurare la dimensione fisica di un oggetto reale o di
un’immagine si usano gli strumenti convenzionali meccanici: metro, doppio decimetro,
calibro, compasso, ecc. Il tempo si misura con il cronometro o con frequezimetri quando
l’evento è ripetitivo. I tester e i multimetri sono strumenti universali. Essi misurano molte
grandezze elettriche: tensioni, correnti, resistenze, capacità ecc. I tester sono strumenti
elettromeccanici in cui una bobina mobile immersa in campo magnetico ruota se in essa
fluisce una corrente. In linea di principio misura la corrente elettrica ma, con opportune reti
resistive, il tester misura anche valori di tensione. Il multimetro è molto simile al tester ad
eccezione della lettura del valore da quantificare che è dato da un display digitale che
converte il parametro incognito in un numero. L’oscilloscopio è uno strumento che misura
solo valori di tensioni con qualsiasi variabile temporale, la corrente può essere dedotta da una
misura indiretta. Esistono due tipi di oscilloscopi: L’oscilloscopio a raggi catodici e
l’oscilloscopio digitale (il primo è in via d’estinzione). L’oscilloscopio a raggi catodici
utilizza un generatore di elettroni, due coppie di placchette deflettrici ed un schermo
fluorescente. Applicando un potenziale alle placchette deflettrici il fascio di elettroni cambia
direzione ed illumina lo schermo in un punto differente da quello iniziale. Orizzontalmente il
pennello elettronico si muove con velocità costante a causa della differenza di potenziale
linearmente crescente tra la coppia di armature verticali. Proprio lo spazzolamento orizzontale
determina il modo di sincronismo. Il modo di sincronismo può essere automatico, normale o
a singolo impulso. Il primo modo condiziona lo spazzolamento orizzontale del pennello
elettronico in maniera automatica in funzione del segnale d'ingresso ed in particolar modo
dalla frequenza e forma d'onda. Questo modo esegue lo spazzolamento anche in assenza di
segnale da misurare o con segnali continui ed il risultato in questo caso è una linea
orizzontale sullo schermo. Quando il segnale d'ingresso non è ripetitivo o è ripetitivo ma con
una forma d’onda variabile o complessa, allora è necessario utilizzare il modo normale. In
questo modo è necessario fissare dall'esterno le condizioni di spazzolamento del fascio
elettronico. Cioè, si condiziona il fascio ad eseguire lo spazzolamento ogni qulavolta il
segnale d'ingresso presenta un fissato valore di ampiezza e una derivata positiva o negativa.
Infine, il modo a singolo impulso prevede pure la predeterminazione delle condizioni del
segnale d'ingresso come nel caso del modo normale ma necessita di un ok da parte
dell'operatore per ogni spazzolamento che si vuole eseguire; praticamente si deve armare lo
strumento prima di registrare un segnale poiché lo spazzolamento viene eseguito una sola
volta. Questo sistema è molto utile quando si lavora in ambienti molto disturbati
elettromagneticamente ed è necessario che lo spazzolamento sia unico.
Il display dell’oscilloscopio è diviso in quadratini e ogni quadratino è diviso in cinque
parti. Pertanto dal valore della scala orizzontale e della scala verticale si può risalire al valore
della più piccola divisione che corrisponde, per ogni asse, ad un quinto del valore di ogni
quadratino. Chiaramente anche il più piccolo valore di lettura corrisponde ad un quinto del
valore della scala e poiché l’errore associato è la metà del più piccolo valore di lettura, esso
corrisponde a  un decimo del valore della scala. Se la misura prevede due letture allora
l’errore associato è  2*1/10 del valore della scala; se invece la misura prevede un valore di
riferimento fissato dall’operatore, allora si può considerare la misura come determinata da
una sola lettura e l’errore associato è  1/10 del valore della scala.
2
Un limite dell’oscilloscopio è il valore massimo della frequenza del segnale che può
registrare; la banda passante. Questo valore è condizionato sia dall’amplificatore verticale che
dalle placchette deflettrici; cioè se le placchette sono lunghe ed il tempo degli elettroni per
attraversarle è più grande del tempo con cui il segnale cambia valore, allora il risultato di
lettura è un fallimento. Una soluzione a questo problema è diminuire la lunghezza delle
placchette ma si perde in sensibilità. Gli ultimi oscilloscopi convenzionali erano corredati da
un sistema multiplo di placchette formanti una linea di trasmissione. Questo sistema aveva
permesso di aumentare la banda passante fino a 100MHz. La caratteristica della banda
passante può anche essere espressa con un tempo, cioè il tempo di salita del fronte di un
impulso pari a circa un quarto del periodo di un’onda sinusoidale; cioè la variazione della
tensione nel tempo è approssimativamente la stessa nei due casi. In pratica si usa la seguente
relazione per passare dalla banda passante al tempo di salita;
350
tr 
(ns )
f ( MHz )
t r è il tempo di salita. Il tempo di salita è definito come il tempo necessario a portare il
valore dell’impulso dal 10% al 90%. Dalla relazione sopra, possiamo concludere che
l’oscilloscopio non può visualizzare impulsi con tempi di salita più piccoli di t r .
Ammettendo un tempo di salita, t s , intrinseco all’impulso da diagnosticare, il tempo di salita
dell’impulso mostrato dall’oscilloscopio dipenderà sia da t s che da t r mediante la seguente
relazione:
t t  t s2  t r2
t t è il tempo totale.
L’oscilloscopio digitale consta principalmente di un amplificatore verticale, di un clock
circuito, di una memoria ecc. Il segnale viene campionato con una velocità di campionamento
chiamata sampling rate. In pratica l’oscilloscopio registra i valori del segnale d’ingresso non
in maniera continuativa come nell’osciloscopio tradizionale, ma a determinati intervalli di
tempo. Successivamente questi valori vengono visualizzati dal dispay come singoli punti o
uniti con una spezzata o con una curva. Il modo real time sampling acquisisce la forma
d’onda dell’impulso registrando un solo “spazzolamento”. Il segnale ideale ( t s =0) può essere
presentato dal display con tempo di salita di circa 0.8 a 1.6 l’intervallo di campionamento in
funzione del trigger.
3
Misura della differenza di potenziale mediante l’oscilloscopio
Per la misura della d.d.p. si usano delle sonde per collegare il circuito elettrico
all’oscilloscopio; esse sono di due tipi: semplici e compensate. Le prime introducono una
capacita’ di 100 pF/m mentre le seconde un’impedenza resistiva molto alta.
Avendo a disposizione un generatore di segnale, prima di iniziare l’esperimento misurare
la resistenza interna del generatore quando questi fornisce un segnale sinusoidale con un
valore di frequenza ~ 1 kHz .
Fissare una tensione Vi di ingresso ed azzerare l’oscilloscopio nella parte bassa del display
in modo da leggere solo la tensione massima dell’onda ed associare un solo errore di lettura.
Fare misure con la sonda semplice e graficare i dati con scale semi-log.
Determinare la frequenza di taglio utilizzando (al valore V0/) i due valori sperimentali
della frequenza letti con l’oscilloscopio e i due sperimentali letti con il generatore piu`
prossimi al valore teorico.
Utilizzare il metodo della propagazione degli errori e dei minimi quadrati, per determinare
il risultato finale:
x
i 2i
1
1
i
 i 2
Xi = xi + i ; X 
;
2
1
m
i

i
2
i
dove xi e’ il valore della frequenza, i e’ l’errore massimo associato, X e` il valore medio e
m e` il suo errore.
Tarare la sonda compensata e fare le stesse misure.
Graficare i risultati
R0
Sonda s emplic e
Ci rcuito equival ente
OS
R0
OS
Ro s
Cos
Ros
Ceq=Ccavo + Cos= 1/Rceq
4
Ceq
Circuito CR
C
R
Vi
VU
Fig. 1
Schema elettrico di un circuito CR
Scegliere un condensatore C ed un resistore R in modo che il prodotto RC sia compreso tra
10 ms e 1s; (1  50 k, 1  200 nF). Trovare la funzione di trasferimento e la funzione di
trasferimento approssimata per |p
Utilizzare una sonda semplice ed una compensata per la misura, rispettivamente, di Vi e
Vu.
Verificare se e’ un filtro passa alto.
Calcolare il valore della frequenza di taglio e confrontarlo con quello teorico.
Calcolare lo sfasamento alla frequenza di taglio e confrontarlo con quello teorico. Per fare
questa misura sincronizzare l’oscilloscopio con la traccia che risulta in anticipo e misurare la
differenza di tempo t di slittamento delle due onde. Lo sfasamento risulta =t .
Trovare il range di frequenza dentro cui la tensione di uscita e’ la derivata dell’ingresso.
Confrontare i risultati sperimentali con i valori teorici.
Studiare il comportamento del circuito quando e` eccitato con un gradino di potenziale.
(Per ottenere quest’ultimo si puo` utilizzare anche un’onda quadra con un offset negativo.)
Determinare sperimentalmente l’insieme dei valori della durata dell’impulso che subisce
una derivata dal circuito.
Per la misura del tempo  fare una foto e determinare l’intersezione con l’asse x della
derivata calcolata al tempo t=0.
5
Circuito RC
R
C
VU
Vi
Fig. 2
Schema elettrico di un circuito RC
Scegliere un condensatore C ed un resistore R in modo che il prodotto RC sia compreso tra
10 ms e 1s; (1  50 k, 1  200 nF).
Utilizzare una sonda semplice ed una compensata per la misura, rispettivamente, di Vi e
Vu. Trovare la funzione di trasferimento e la funzione di trasferimento approssimata per
|p
Verificare se e’ un filtro passa basso e calcolare il valore della frequenza di taglio.
Confrontarlo con quello teorico. Calcolare lo sfasamento alla frequenza di taglio e
confrontarlo con quello teorico. Per fare questa misura sincronizzare l’oscilloscopio con la
traccia che risulta in anticipo e misurare la differenza di tempo t di slittamento delle due
onde. Lo sfasamento risulta =t .
Trovare il range di frequenza dentro cui la tensione di uscita e` l’integrale del segnale di
ingresso. Confrontare i risultati sperimentali con i valori teorici, cioè verificare il rapporto
Vu/Vi e lo sfasamento.
Studiare il comportamento del circuito quando e` eccitato con un gradino di potenziale.
Determinare sperimentalmente l’insieme dei valori della durata dell’impulso la cui uscita
rappresenta un segnale integrato. Poichè in questo caso non si ha un singolo impulso di
tensione ma bensì un’onda quadra, allora fissando il tempo t=0 come in Fig. 3 considerare
t
l’integrale proprio da questo punto. La Vu(T) corrisponde all’integrale di
 Vidt . Verificare
0
ciò per t=T; cioè l’area tratteggiata in Fig. 3 deve corrispondere all’ampiezza del segnale di
uscita al tempo T.
Vi
Vu
uu
T
3T
Fig. 3
Forme d’onda della tensione di ingresso e di uscita in funzione del tempo
6
Circuito LC Oscillante
Scopo di questa esperienza e’ lo studio di un circuito oscillante realizzato mediante un
condensatore e un induttore (Fig. 1).
Rg
cv
c0
L
VU
Vi
Fig. 1
Schema elettrico di un circuito LC oscillante
Si ha a disposizione un generatore di onde quadre Stanford con impedenza di uscita di 50
 un condensatore di capacita’ 10 - 500 nF, una sonda compensata, un cavo coassiale e il
materiale per la realizzazione di un induttore.
Realizzare un induttore costruendo un solenoide sul supporto a disposizione.
Il valore teorico di L e’ dato dalla relazione L = Kon2 A = KoN2A/ dove o=1.26 10-6
H/m e’ la permeabilita’ magnetica, n la densita’ di spire, la lunghezza A la sezione, N il
numero di spire del solenoide e K un coefficiente adimensionale (Fig. 2) dipendente dal
rapporto diametro/lunghezza del solenoide.
K
1
0.8
0.6
0.4
0.2
0.1
0. 2
0.5
1
2
5
10
20
D/
Fig. 2
Dipendenza del fattore K dal rapporto diametro/lunghezza
Realizzare il circuito come mostrato in Fig. 1.
Applicando in ingressso un’onda quadra di ampiezza massima Vo, la tensione di uscita
2V  t
1
1
sara` Vu  0 e  sin(t ) dove =2RC (costante di tempo) e  
(la

2 2

LC
4R C
pulsazione).
Il valore della resistenza R corrisponde al parallelo Rg//Rp, dove Rp e’ la resistenza
equivalente parallela dell’induttore e il valore della capacita’ C=C0+Cv dove Cv e’ la capacita
del cavo coassiale di collegamento.
7
Rp
Rg
I
C
Rp
L
C
R
VU
L
I
a
VU
b
Fig. 3
a) schema elettrico del circuito oscillante; b) schema elettrico equivalente
Supponendo di conoscere la capacita` C, dalla pendenza dell’inviluppo della forma d’onda
di uscita ricavare il valore R e di conseguenza calcolare Rp . Per valutare la resistenza del filo
che costituisce il solenoide e’ necessario trasformare il circuito Rp //L in un circuito Rs serie
L.
Rp
L
Rs
L
a
b
Fig. 5
a) Rappresentazione parallelo di Rp //L; b) Rappresentazione serie di Rp //L
Confrontando il valore teorico di  con quello sperimentale e` possibile avere
informazioni sulla corretteza del valore di L.
8
Studio del campo elettro-magnetico prodotto da una bobina
Si ha a disposizione una bobina principale con le caratteristiche geometriche ed elettriche
indicate sul supporto, una bobina rivelatrice, un generatore di segnali, elementi di circuito e
strumenti.
Per generare un campo magnetico alimentare la bobina con un’onda sinusoidale fornita dal
generatore. Per misurare la corrente circolante nella stessa inserire in serie alla bobina un
resistore in modo che dalla caduta di potenziale sullo stesso si possa risalire alla corrente
nella bobina. La scelta della resistenza deve essere fatta tenendo presente la resistenza interna
del generatore che non deve risultare piu` piccola dell’impedenza del circuito RLp. Realizzare
il circuito di Fig. 1 facendo attenzione alla posizione della massa.
Lp
Lr
SC
R
Fig. 1 Circuito generatore di campo e circuito rivelatore: Lp induttanza della bobina
principale R resistore, Lr induttanza della bobina rivelatrice ,SC sonda compensata
Dalla teoria calcolare l’intensita` del campo magnetico all’interno della bobina.
Misurare la f.e.m. indotta nella bobina rivelatrice in punti vicini alla bobina principale e
confrontare il segnale indotto con quello di corrente presente nel resistore e verificare se la
f.em. indotta soddisfa alla seguenta relazione
Vfem=cost d/dt
Per questa misura utilizzare la sonda compensata onde evitare effetti di assorbimento che
potrebbero intervenire a causa della capacita` della sonda semplice.
Approssimando la bobina rivelatrice ad N spire uguali avvolte sullo stesso punto, valutare
l’intensita` e la direzione del campo magnetico nello spazio intorno alla bobina principale.
Fare una mappa dell’intensita` e direzione del campo magnetico.
Per misuarare direttamente il campo magnetico e` necessario integrare il segnale della
bobina rivelatrice. Progettare pertanto un circuito integratore RC alla frequenza da voi scelta
e collegarlo in cascata alla bobina rivelatrice (Fig. 2).
R
C
Lr
Fig. 2
Schema elettrico del circuito RC integratore
Affinche` il nuovo circuito RC funzioni correttamente da integratore del segnale indotto la
sua impedenza deve essere molto maggiore dell’impedenza della bobina rivelatrice. Per
9
valutare la presenza del campo magnetico collegare un elettrodo sonda al conduttore centrale
della sonda compensata. A distanze piu` lontane dalla sorgente il campo elettrico sara`
sicuramente molto basso e pertanto e` piu` conveniente utilizzare una sonda semplice con un
elettrodo di pochi centimetri di lunghezza. In questo modo si evita l’attenuazione della sonda
compensata ma non si puo` evitare la presenza della capacita` della sonda ed affinche` si
abbia un segnale leggibile con l’oscilloscopio scegliere una frequenza del segnale del
generatore che porti in risonanza il circuito rivelatore e che enfatizzi il segnale di uscita.
10
Caratteristica statica e dinamica di un diodo
Si ha a disposizione un diodo di cui si vuole conoscere la caratteristica. Per determinare la
caratteristica in polarizzazione diretta montare il circuito come in Fig. 1a, dove
l’amperometro e` a monte mentre l’oscilloscopio e` direttamente collegato al diodo. Lo scopo
di questo collegamento e` di evitare la lettura della c.d.p. nell’amperometro da parte
dell’oscilloscopio. L’alimentatore a disposizione fornisce una tensione da 0 a 40 V. Pertanto,
nonostante questa peculiarita` dell’alimentatore, e` necessario introdurre una resistenza in
serie all’alimentatore onde permettere un miglior controllo della tensione applicata al diodo e
limitare la massima corrente. La scelta della resistenza RL e` vincolata dalla potenza del diodo
e dal valore massimo di tensione di alimentazione che si vuole utilizzare. Per esempio, in un
diodo al Si da 1W la corrente massima e` ~ 1600 mA, pertanto se la tensione massima di
alimentazione e` 20 V il valore della resistenza necessaria affinche` la corrente non superi i
600 mA deve essere maggiore di 13 . E` comunque buona norma sperimentale scegliere
valori di resistenze limitatrici piu` alti di quelli calcolati e solo durante l’esperienza si valuta
l’opportunita` di scegliere valori piu` bassi.
RL
A
ID
G
D
VD
V
Fig 1a
RL
A
ID
G
D
VD
V
Fig. 1b
Schema elettrico del circuito utilizzato per misurare un diodo in polarizzazione diretta
(Fig. 1a) ed in polarizzazione inversa (Fig.1b)
Per determinare la caratteristica in polarizzazione inversa si modifica il circuito come in
Fig 1b. In questo caso la strumentazione a disposizione potrebbe non permetterci di rilevare i
valori di corrente essendo questi troppo bassi. Comunque il valore di corrente che si deve
attribuire e` inferiore al valore dell’errore di lettura.
Conoscere la caratteristica di un elemento circuitale in condizioni dinamiche, cioe` con
correnti alternate, e` spesso di grande utilita`. Percio` proviamo ad ottenere la catteristica
dinamica di un diodo polarizzandolo con tensioni alternate e ponendo la corrente sull’asse y e
la tensione sull’asse x dell’oscilloscopio. Essendo l’oscilloscopio uno strumento con un
terminale a massa e` necessario avere il segnale di tensione e quello di corrente riferiti alla
massa.
Realizzare il circuito di Fig 2.
Come si vede dalla Fig. 2 solo il valore di corrente e` riferito alla massa mentre la c.d.p. ai
capi del diodo e` sovrapposta al potenziale presente sulla resistenza Rl. Solo se la c.d.p. su Rl
e` trascurabile rispetto alla c.d.p. ai capi del diodo allora possiamo approssimare la tensione
misurata dall’oscilloscopio come la tensione ai capi del diodo. Come si sceglie il valore di Rl
11
? Il valore di Rl deve essere inferiore a Req. Quest’ultimo valore lo si puo` valutare dalla
caratteristica statica determinata precedentemente. Per esempio supponendo una tensione di
0.7-0.8 V, in corrispondenza di questi valori la caratteristica statica fornisce il corrispondente
valore di corrente e dal rapporto V/I si conosce il valore di Req. Puo` succedere di scegliere un
valore di R2 molto piccolo e di non essere in grado di misurare la corrente, in questo caso si
consiglia di valutare la scelta caso per caso durante l’esperienza.
ID
D
VD
RF
y
F
RI
x
O
Fig. 2
Schema elettrico del circuito utilizzato per determinare la caratteristica di un diodo in
condizioni dinamiche
Iniziare l’esperienza ponendo il segnale di corrente sulle ordinate e quello di tensione sulle
ascisse via il canale a e centrare il fascio elettronico al centro del display fissando la
frequenza del segnale di alimentazione a 50 Hz. Aumentare gradualmente il valore di
tensione fino alla comparsa della curva caratteristica. Graduare correttamente le scale x-y,
fare una foto e studiare il comportamento della curva in funzione della frequenza.
12
Capacita’ della giunzione di un diodo
La capacita` della giunzione di un diodo e` C =  s/w dove  e` la costante dielettrica, s e`
la sezione e w e` la larghezza della giunzione.
Il circuito equivalente di un diodo in regime dinamico e’ illustrato in Fig. 1
C
RS
D
RP
Fig. 1
Circuito equivalente di un diodo in regime dinamico
con Rs resistenza del corpo del diodo ~ 0 e Rp resistenza della giunzione. Rp e` ~ 0 per
polarizzazione diretta e  per polarizzazione inversa.
D
F
B
R
V
Fig. 2
Schema elettrico del circuito
Montare il circuito come in Fig 2 con R =500 - 500 k e alimentare con un onda quadra.
Studiare il comportamento della corrente nel circuito al variare della tensione di ingresso:
a) fissare prima la tensione a valori inferiori di quello di conduzione del diodo e rilevare i
valori di tensione ai capi della resistenza R. Da questi ultimi ricavare i relativi valori della
capacita` in polarizzazione diretta ed inversa, cioe` dalla costante di tempo della risposta (Cdir
= dir/R e Cinv = inv/R).
b) fissare la tensione a valori superiori a quello di conduzione e rilevare i valori di tensione
ai capi della resistenza R. Da questi ultimi ricavare i relativi valori della capacita` in
polarizzazione diretta ed inversa. In questo caso il valore della resistenza Rp cambia
sensibilmente al variare del segno della tensione, pertanto durante la fase di interdizione la
capacita` si calcola come nel caso precedente mentre in polarizzazione diretta e` necessario
risolvere il circuito di Fig. 3, dove Rp e ` differente da 0.
13
C
R
RP
Fig. 3
Circuito equivalente in polarizzazione diretta
Per esercitazione risolvete il circuito e confrontate il risultato con la soluzione qui sotto
riportata:
t
Rp  ReC
V0
I0 
(1 
e
)
R  Rp
R
dove Re e` data da (RpR)/(R+Rp).
Dal risultato sperimentale potete notare che in fase di polarizzazione diretta la corrente nel
circuito ha un picco in corrispondenza del fronte negativo dell’onda quadra e dopo un po` si
stabilizza ad un valore costante determinando una c.d.p. in R che chiamiamo Vc. Sapendo che
la costante di tempo in questa fase e` dir = Re Cdir determinare Cdir.
Comporre la seguenta tabella con almeno tre valori di tensione nel caso a) e tre nel caso b):
V0(V)
Vinv(V)
Vdir(V)
Vc(V)
14
Cinv(pF)
Cdir(pF)
Raddrizzatore di tensione
L’esperienza si propone di studiare un raddrizzatore di tensione a singola e a doppia
semionda.
Per la realizzazione dell’esperienza si ha a disposizione l’oscilloscopio, multimetri digitali
e un trasformatore di tensione con doppia uscita da 5 e 10 V.
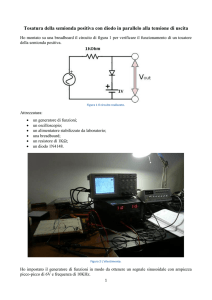
Montare il circuito come in Fig. 1 utilizzando un diodo raddizzatore (1N4007) e l’uscita a
10 V del trasformatore. Il valore della resistenza Rc deve essere compreso tra 100 e 560 .
D
220 V ~
50 Hz
Vi
Rc
i
Vu
T
Fig. 1
Schema elettrico di un circuito raddrizzatore a singola semionda
Studiare il comportamento del segnale ai capi di Rc. Scegliere un condensatore elettrolitico
di capacita’ compresa tra 47 F e 470 F e collegarlo come in Fig. 2.
D
220 V ~
50 Hz
C
Vi
Rc
Vu
T
Fig. 2
Schema elettrico di un circuito raddrizzatore a singola semionda
Studiare il segnale di tensione ai capi di Rc. Calcolare il fattore di ripple dalla relazione
teorica r=5.8/RC e confrontarlo con il valore sperimentale r  V
, dove V e` la
2 3Vm
parte variabile della tensione e Vm il suo valore medio.
Ripetere lo stesso esperimento utilizzando un ponte di diodi (WL10F) realizzando il
circuito di Fig. 3.
220 V ~
50 Hz
Vi
 +
-
C1
Rc
Vu
T
Fig. 3
Schema elettrico di un circuito raddrizzatore a doppia semionda
15
Raddrizzatore stabilizzato con diodo Zener
Questo circuito lo si realizza con un diodo zener. Graficare la curva caratteristica del diodo
zener che si ha a disposizione (BZY 97C12) e determinare il valore di Izmin necessario per
avere la conduzione di zener.
Progettare il valore di Rs da porre in serie al circuito come illustrato in Fig. 1
D
220 V 

50 Hz
Rs
C1
V
Iz
Dz
VZ
Rc
T
Fig. 1
Schema elettrico di un circuito raddrizzatore a singola semionda stabilizzato
con Rs  (Vmin-Vz)/(Izmin+Ic)
Montare il circuito come in Fig. 1. Ora lo stesso carico Rc e` sottoposto ad una tensione
piu` stabile. Misurare il fattore di ripple e confrontatelo con quello della precedente
esperienza.
Per migliorare ulteriormente il fattore di ripple provare ad aggiungere ai capi di Rc un
condensatore con valore di capacita` circa uguale a C1.
Fare attenzione alla potenza dissipata da Rs.
16
Luxmetro
Un diodo p-n se polarizzato inversamente conduce la bassissima corrente di
saturazione. Se invece è illuminato la corrente inversa aumenta e può essere utilizzato come
misuratore di flusso luminoso. Al buio la corrente inversa è dovuta ai portatori minoritari
generati termicamente. Quando la giunzione è illuminata con radiazione che genera coppie la
corrente inversa aumenta. Cioè, immaginando la generazione di coppie elettrone-lacuna nel
semiconduttore esse portano ad una nuova concentrazione delle cariche che non rispetta
quella dovuta dalla statistica di Fermi-Dirac. Pertanto i portatori minoritari migrano verso la
giunzione per ristabilire l’equilibrio.
Fig. 1. Livelli energetici e migrazione di cariche
corrente
Fig. 2. Circuito per la misura della
In un fotodiodo inversamente polarizzato la corrente inversa resta constante con la
tensione applicata. D’altronde la corrente è dovuta alla disponibilità delle cariche e non alla
tensione di accelerazione. Aumentando la tensione di accelerazione aumenta,
contemporaneamente, anche il livello di saturazione della giunzione.
La risposta, S, di un fotodiodo è data in A/W cioè la corrente in funzione del flusso
luminoso. Il diodo S1336 dell’Hamamatsu ha una risposta di circa 0.4 A/W e l’aria sensibile
è 1,2 mm2.
Illuminando il diodo possiamo rilevare la corrente e determinare il valore di S. Si può
notare che la corrente generata è insensibile al valore della tensione applicata. Per bassi
livello del flusso incidente si rischia di non essere capaci di leggere la bassa corrente fornita.
Allora, è necessario utilizzare la differenza di potenziale che la corrente provoca nel fluire in
una resistenza. Poiché V=RI per raggiungere valori accettabili di tensione si gioca col valore
della R che aumentandola aumenta pure la caduta di potenziale fino a portarla a valori
leggibili con la strumentazione a disposizione. Questa configurazione può portare il diodo in
saturazione. Cioè, la corrente generata provoca una caduta di potenziale sulla resistenza
uguale alla f.e.m. dell’alimentatore. Essa non può aumentare se non si aumenta la f.e.m.
Ponendo una resistenza di circa 1M la sensibilà dello strumento aumenta notevolmente.
Fig. 3. Circuito luxmetro per la
rivelazione di bassi flussi luminosi.
Fig. 4 Configurazione fisica TO-18
Valutare la luce del sole a circa 500W/m2 ( giornata solare a Lecce ) e ricordare che
1 lux=5x10-6 W/cm2, V0  5 V, S=0,4 A/W.
17
Polarizzazione di un transistor ad emitter comune
Scopo dell’esperienza e’ la polarizzazione di un transistor, ovvero la scelta dei valori di
tensione e di corrente e le relative resistenze di connessione, mediante il metodo grafico ed
analitico.
Per quest’esperienza si ha a disposizione:
a) un generatore di tensione continua
b) un multimetro digitale
c) un transistor con le relative curve caratteristiche
d) oscilloscopio
IB
RB
IC
RC
C
+
B
Vcc
VB
E
VC
TR
IE
Fig. 1
Schema elettrico del circuito utilizzato per polarizzare un transistor nella configurazione
ad emettitore comune
Metodo grafico
Tenendo conto della potenza massima dissipabile dal transistor scegliere un punto di
lavoro P(VCEL, ICL, IBL) sulle caratteristiche di uscita. Scelto il valore di VCC tracciare la retta
di carico e determinare il valore di RC.
Dalla relazione VCC=RBIBL + VBE determinare il valore di RB.
Montare il transistor nella configurazione ad emettitore comune come in Fig. 1, misurare
le tensioni VBE, VCEL, ricavare le correnti ICL e IBL ed il parametro hFE e confrontarli con i
valori di progetto.
Metodo analitico
Determinare VCEL , ICL ed hFE dalle condizioni di test fornite dal costruttore.
Determinare RC dalla relazione RC=(Vcc-VCEL)/ICL e RB dalla relazione RB=(VccVBE)hFE/ICL.
Montare il transistor nella configurazione ad emettitore comune come in Fig. 1, misurare
le tensioni VBEL, VCEL , ricavare le correnti ICL e IBL ed il parametro hFE e confrontarli con i
valori di progetto.
18
Amplificatore ad emettitore comune
Scopo dell’esperienza e’ di costruire e studiare un circuito amplificatore utilizzando un
transistor, modello 108 B, collegato nella configurazione ad emettitore comune.
Per quest’esperienza si ha a disposizione:
a) un generatore
b) un alimentatore
c) un multimetro digitale
d) un transistor con le relative curve caratteristiche
e) un oscilloscopio
Scegliere un punto di lavoro nel mezzo della regione attiva e calcolare il valore delle
resistenze di polarizzazione RB ed RC tenendo conto della potenza massima dissipabile dal
transistor.
Montare il circuito come in Fig. 1.
+
VCC
IB
RB
vi
R1

IC
RC
C
Ci
vu
B
R2
VBE
TR
E
VCE
IE
Fig.1
Schema elettrico dell’amplificatore ad emettitore comune
.
+
VCC
RB
C
R1

RX
R2
vi'
Ci
iu
RC
vU
B
vi
ii'
TR
E
Fig. 2
Schema elettrico dell’amplificatore ad emettitore comune modificato per la misura della
resistenza di ingresso Ri.
Scegliere il valore di capacita` del condensatore tra 10 e 1000 nF. Se necessario costruire
un partitore di tensione per diminuire la tensione di ingresso in modo da evitare il
19
funzionamento del transistor in interdizione o in saturazione. Fissare la frequenza del
generatore a qualche kHz e calcolare l’amplificazione di tensione, Av=vu/vi misurando la
tensione di ingresso vi e quella di uscita vu .
Inserire una resistenza nota, Rx, con valore poco piu` alto di hie, tra il condensatore e il
partitore come in Fig. 2. e misurare la corrente di ingresso ii.=(v`i - vi)/Rx. Determinare
l’amplificazione di corrente e la resistenza di ingresso Ri=vi/ii.
Confrontare i valori sperimentali ottenuti con quelli teorici.
20
Amplificatore a collettore comune
Scopo dell’esperienza e’ di costruire e studiare un circuito amplificatore utilizzando un
transistor, modello 108 B, collegato nella configurazione a collettore comune.
Per quest’esperienza si ha a disposizione:
a) un generatore
b) un alimentatore
c) un multimetro digitale
d) un transistor con le relative curve caratteristiche
e) un oscilloscopio
Scegliere un punto di lavoro nel mezzo della regione attiva e calcolare il valore delle
resistenze di polarizzazione RB = (Vcc - VBE)/IB - hFE RE ed RE = (Vcc - VCE)/IC.
Montare il circuito come in Fig. 1.
+
VCC
RB
IB
TR
vi
R1
IC
C
Ci
VCE
B

E
R2
vu
VBE
RE
IE
Fig.1
Schema elettrico dell’amplicatore a collettore comune.
Scegliere il valore di capacita` del condensatore tra 10 e 1000 nF. Se necessario costruire
un partitore di tensione per diminuire la tensione di ingresso in modo da evitare il
funzionamento del transistor in interdizione o in saturazione.
Fissare la frequenza del generatore a qualche kHz e calcolare l’amplificazione di tensione,
Av=vu/vi misurando la tensione di ingresso vi e quella di uscita vu .
21
+
VCC
RB
TR
C
R1
Ci
Rx
B

vU
ii
R2
E
vi'
vi
iu
Fig. 2
Schema elettrico modificato per la misurazione di Ai e Ri.
Inserire una resistenza nota, Rx, di valore poco piu` alto di hic, tra il condensatore e il
partitore come in Fig. 2. e misurare la corrente di ingresso ii.=(v’i - vi)/Rx. Determinare
l’amplificazione di corrente, la resistenza di ingresso Ri=vi/ii e quella di uscita Ru.
+
VCC
RB
TR
C
R1
Ci
A
B

E
R2
RE
B
vU
Rx
v' u
Fig.3
Schema elettrico modificato per la misurazione di Ru.
Per la misura di quest’ultima inserire una resistenza di valore noto come in Fig. 3 e
misurare il valore della tensione di uscita v`u con la resistenza Rx collegata e la tensione vu
quando Rx non e` collegata. Il parallelo R`u = Ru // RE sara` dato dalla relazione:
v  v'
R 'u  n ' u Rx
vu
Determinare la resistenza di uscita Ru.
Confrontare i valori sperimentali ottenuti con quelli teorici.
22
Amplificatore ad emettitore comune autopolarizzato
Scopo dell’esperienza e’ di costruire e studiare un circuito amplificatore autopolarizzato
utilizzando un transistor modello 109 C nella connessione ad emettitore comune.
Per quest’esperienza si ha a disposizione:
a) un generatore
b) un alimentatore
c) un multimetro digitale
d) un transistor 109 C con le relative curve caratteristiche
e) un oscilloscopio
Scegliere un punto di lavoro e calcolare il valore delle resistenze di polarizzazione R1, R2,
RE ed RC dalle relazioni:
RC+ RE = (VCC - VCE)/ IC con RE IE ~ 1 - 2 V
R1 = (VCC - VB)/ (IB +I1)
R2 = VB/I1
VB = VBE + REIC
I1 > 8 IB
Montare il circuito come in Fig. 1 senza il condensatore CE, senza il carico RL. Verificare
il punto di lavoro.
+
VCC
R1
I1
RC
IC
C
Rs
Ci
CU
RL
B

R2
I1
TR
vu
E
IE
RE
CE
Fig. 1
Schema elettrico dell’amplificatore autopolarizzato
Determinare l’amplificazione di tensione e di corrente e confrontarle con i valori teorici.
Aggiungere un condensatore CE di capacita` compresa tra 40 nF e 100 F e un carico RL di
circa 1000 ; misurare l’impedenza di ingresso e di uscita vista da RL e l’amplificazione di
tensione in funzione della frequenza.
Verificare i risultati con quelli teorici ricordando che il valore della frequenza di taglio
inferiore 1 e` limitato da 1/hie Ci, 1/((Ru+RL)Cu), hfe/(hie CE).
23
Oscillatore a sfasamento
Scopo dell’esperienza e` di progettare e costruire un oscillatore sinusoidale a sfasamento
utilizzando un amplificatore a transistor.
Per quest’esperienza si ha a disposizione:
a) un alimentatore
c) un multimetro digitale
e) un oscilloscopio
Per realizzare l’oscillatore utilizzare l’amplificatore con transistor 109C ed una rete
sfasatrice formata da tre celle CR uguali collegate in cascata come mostrato in Fig. 1.
+
VCC
RB1
RC
C1
C2
C3
C
vu
B
R1
RB2
TR
R2
R3
E
CE
RE
Fig. 1
Schema elettrico di un oscillatore a sfasamento
Scegliere il valore della capacita` compreso tra 10 nF e 1 F ed il valore della resistenza
tra 1 e 5 k. Verificare che la seguente relazione sia soddisfatta:
hfe > 4RC/R + 23 + 29 R/RC
Visualizzare la forma d’onda presente sul collettore e verificare che la frequenza di
oscillazione sperimentale sia uguale a quella teorica:

1
R 
2RC 6  4 C 
R
Fare una foto della forma d’onda.
24
Multivibratore astabile
Scopo dell’esperienza e` di progettare e costruire un miltivibratore astabile a transistor.
Per quest’esperienza si ha a disposizione:
a) un alimentatore
c) un multimetro digitale
e) un oscilloscopio
Realizzare il multivibratore seguendo lo schema di Fig. 1 utilizzando transistor BC108 o
un integrato TBA 331.
RC
RB
RB
C1
RC
C2
+
VCC
VU
TR2
TR1
Fig. 1
Schema elettrico di un multivibratore astabile
Calcolare le resistenze di polarizzazione RC dalla relazione:
RC = VCC/ICmax
La corrente di base e` calcolata dal valore di ICmax/hFE. Poiche` hFE ha valori massimi e
minimi dobbiamo assicurare il funzionamento anche per valori minimi di hFE. Pertanto il
minimo valore di IB che dobbiamo assicurare risulta da IB=ICmax/hFEmin .
La resistenza RB e` data dalla relazione:
RB  (VCC-VBE)/IB
Verificare che all’uscita vi sia un’onda quadra e confrontare i valori sperimentali della
tensione alta TH e del periodo avente tensione bassa TL con le relazioni:
TH = ln2 RBC1 e TL = ln2 RBC2.
Fare una foto della forma d’onda.
25
Studio dei fenomeni di diffrazione
Scopo di questa esperienza e` lo studio dei fenomeni diffrazione prodotta da aperture
circolari e da una fenditura stretta.
Utilizzare come sorgente luminosa un laser He-Ne (=632.8 nm) e dirigere il fascio
luminoso perpendicolarmente verso un foro circolare, raccogliendo la luce su di uno schermo
posto come in Fig. 1.
d
x

o
Laser He-Ne
Perturbazione
Schermo
Fig.1
Schema dell’apparato sperimentale utilizzato per lo studio dei fenomeni di diffrazione
La legge che governa i fenomeni per una perturbazione circolare e` dalla dalla relazione:
D sin=1.22 
dove D e` il diametro del foro e  e` l’angolo sotteso dal raggio del disco di Airy visto
dalla perturbazione.
Determinare il diametro D dell'apertura.
La misura deve essere eseguita ponendo lo schermo a distanze d sufficientemente grandi in
modo da avere una dimensione del disco di Airy accettabile che renda gli errori non troppo
grandi e di essere in condizioni di diffrazione di Fraunhofer.
Utilizzare adesso una fenditura stretta e verificare la legge della diffrazione
a sin= n 
dove a e` la larghezza della fenditura, n l’ordine dei minimi e  l’angolo sotteso dall’asse
principale ed il raggio in corrispondenza del minimo n.
26
Studio dei fenomeni di interferenza
Scopo di questa esperienza e` lo studio dei fenomeni di interferenza prodotti da una doppia
fenditura e da un reticolo di diffrazione in trasmissione ed in riflessione.
Utilizzare come sorgente luminosa un laser He-Ne (=632.8 nm) e dirigere il fascio
luminoso perpendicolarmente verso la pertubazione e raccogliere la luce su di uno schermo
posto come in Fig. 1.
d
x

o
Laser He-Ne
Perturbazione
Schermo
Fig.1
Schema dell’apparato sperimentale utilizzato per lo studio dei fenomeni di interferenza.
Doppio foro: La perturbazione è una coppia di fori investiti dal facsi laser. In questo
esperimento si deve misurare l’intensità luminosa nei punti di interferenza costruttiva e
distruttiva mediante il fotodiodo. I risultati poi, devono essere confrontati con quelli ottenuti
dalla figure di diffrazione da un singolo foro.
Doppia fenditura: Verificare se la posizione dei massimi principali e dei minimi seguono
le leggi :
a sin = n
b sin = n
con a distanza tra le due fenditure, b larghezza della singola fenditura e  angolo sotteso
dalla distanza tra il fascio non perturbato e i massimi o minimi considerati.
Utilizzare adesso un reticolo di diffrazione in trasmissione posto perpendicolarmente al
fascio come in Fig. 1.
Per controllare la posizione del reticolo posizionare il reticolo stesso sul rotatore e
controllare il fascio riflesso di ordine zero che coincida con il fascio laser non perturbato. Il
valore dell’angolo letto sul nonio corrisponde all’angolo di incidenza zero. Per la misura degli
angoli dei fasci utilizzare gli schermi perpendicolari e paralleli al fascio principale come in
Fig. 2.
Verificare che i massimi seguano la legge a sin = n con a distanza tra due fenditure
adiacenti e  l’angolo compreso tra il raggio del massimo di ordine n e la normale al reticolo.
Ruotare ora il reticolo di un angolo a piacere e verificare che i massimi seguono la legge:
a (sin i + sin d) = n
dove i e` l’angolo di incidenza del fascio laser rispetto alla normale del reticolo, d e`
l’angolo sotteso dalla distanza tra la normale e i massimi principali.
Ripetere l’esperimento con un reticolo in riflessione con le stesse modalita` prima esposte.
27
Schermo Parallelo
0
x
Schermo Perpendicolare
x
i
0
Laser He- Ne
Reticolo
d
Fig 2.
Schema dell’apparato sperimentale utilizzato per lo studio dei fenomeni di interferenza da
un reticolo in trasmissione ed in riflessione
28
Monocromatore
Scopo dell’esperienza e` la determinazione dello spettro di emissione di una lampada a gas
incognita utilizzando un monocromatore. Questo dispositivo permette di selezionare una
fascio luminoso avente lunghezza d’onda ben definita.
Porre una lampada vicino alla slit di ingresso del monocromatore ed il fotodiodo vicino
alla slit di uscita come mostrato in Fig. 1.
Monocromatore
Fotomoltiplicatore
Lampada
Oscilloscopio
Fig. 1
Schema dell’apparato sperimentale utilizzato
Prima di iniziare la misura e` indispensabile calibrare lo strumento. Un metodo grossolano
consiste nel portare il valore della lunghezza d’onda letta sulla manopola del monocromatore
al valore =0. In queste condizioni il reticolo funziona da specchio, cioe` tutti i raggi di
qualsiasi lunghezza d’onda emergono dalla slit di uscita. Per essere sicuri che cio` avvenga
ruotare la manopola fino ad ottenere il massimo segnale dalla fotocellula. Assegnare questo
valore letto sul monocromatore come =0. La differenza tra lo zero della manopola e quello
assegnato servira` per correggere tutte le letture.
Ruotare la manopola del monocromatore fino ad avere un massimo registrato dal
fotodiodo ed associare ad esso la lunghezza d’onda letta sul monocromatore. La serie di
massimi cosi` individuata permette, per confronto con valori gia` tabulati, di determinare il
tipo di lampada impiegata.
29
Misura sperimentale della costante di Planck
Scopo di questa esperienza e` determinazione sperimentale della costante di Planck.
Porre la lampada al mercurio vicino la slit di ingresso del monocromatore e la fotocellula
vicino la slit di uscita come in Fig. 1.
+
V
A
Monocromatore
A
Lampada
a
mercurio
K
Fotocellula
Fig. 1
Schema dell’apparato utilizzato
Quindi polarizzare la fotocellula in modo da avere un controcampo che si opponga al
flusso di elettroni uscente dal catodo ed utilizzare un voltmetro ed un amperometro per
leggere la tensione di polarizzazione e la corrente anodo - catodo.
Utilizzando il monocromatore selezionare una delle lunghezza d’onda di emissione della
lampada e leggere la tensione di controcampo alla quale la corrente si annulla.
Ripetere la stessa operazione per le diverse lunghezze d’onda.
Riportare in un grafico le tensioni di controcampo al variare delle lunghezza d’onda
selezionata con il monocromatore e verificare che si abbia un andamento lineare.
Essendo la relazione teorica V = (h/e)  - w dove V e` il potenziale, h la costante di
Planck, e la carica elettrica,  la la frequenza e w la funzione, lavoro ricavare h dalla
pendenza della retta.
In quest’esperienza controllare se esistono correnti di verso opposto aumentando
ulteriormente la tensione. Questa corrente potrebbe essere emessa dall’anodo o dal bulbo
della fotocellula. In questo caso quando l’amperometro legge una corrente nulla non significa
che il catodo non emette ma che la sua corrente e` controbilanciata da quella dell’anodo o da
bulbo.
La tensione da considerare in questa esperienza e` quella che annulla l’emissione dal
catodo e che corrisponde a quel valore di tensione per cui la corrente diviene opposta e
costante.
30