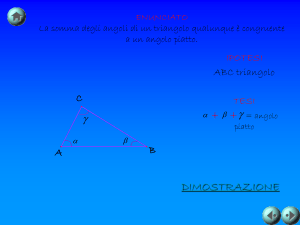
Le rette nella geometria iperbolica
In queste note vediamo alcune prime conseguenze sul comportamento delle rette, che
seguono dalla negazione del quinto postulato euclideo. Per approfondimenti si può fare
riferimento a numerosi testi, tra i quali, ad esempio, segnaliamo Nikolaj Vladimirovic Efimov,
Higher Geometry, Mir, Moscow, 1980; Evandro Agazzi e Dario Palladino, Le geometrie non
euclidee e i fondamenti della geometria, ETS Mondadori, Milano 1978; Roberto Bonola. La
geometria non-euclidea. Esposizione storico-critica del suo sviluppo, Zanichelli, Bologna, 1906
(testo di cui ci sono numerose traduzioni in lingua inglese, più recenti ed ampliate, con il titolo
Non-euclidean geometry) .
Assumiamo tutti i postulati euclidei (espliciti ed impliciti) con l’eccezione del quinto, ossia
assumiamo gli assiomi di Hilbert di appartenenza, di ordinamento, di congruenza e di
continuità e tutte le loro conseguenze. Per indicare due rette complanari e prive di punti in
comune non useremo l’espressione euclidea di “rette parallele” ma diremo semplicemente
“rette che non si intersecano”, riservando la prima espressione ad una situazione particolare
che sarà evidenziata nel corso della trattazione. Quindi le proposizioni 27 e 28 del primo libro
degli Elementi di Euclide, condizioni sufficienti al parallelismo euclideo, continuano a valere
come condizioni sufficienti al non intersecarsi: in particolare due rette aventi una
perpendicolare comune non si intersecano. Assumiamo inoltre la negazione del quinto
postulato euclideo, nella forma del postulato di unicità, e la chiamiamo
Assioma di Lobatchevski - forma debole. Nello spazio esistono una retta r ed un punto P
esterno ad essa tali che per P passano almeno due rette distinte complanari con r e non
intersecanti r.
Enunciamo anche il seguente
Assioma di Lobatchevski - forma forte. Data una qualsiasi retta r nello spazio, per ogni
punto P esterno ad essa passano infinite rette distinte complanari con r e non intersecanti r.
1. Osservazione. E’ chiaro che la forma forte dell’assioma di Lobatchevski implica quella
debole. Tuttavia è vero anche il viceversa come segue dalle successive proposizioni 2 e 3.
La geometria, che assume assieme a tutti gli altri postulati ordinari la negazione del quinto,
viene detta geometria iperbolica.
2. Proposizione. Se esistono una retta r ed un punto P esterno ad essa tali che per P passano
almeno due rette distinte complanari con r e non intersecanti r, allora per P ne passano infinite
con la stessa proprietà.
Dim. Dall’assioma di Lobatchevski, per P passano due rette distinte s e t, complanari con r e
non intersecanti r. La retta s divide il piano in due semipiani e la retta r è contenuto in uno
solo di questi. Prendiamo su t un punto T appartenente al semipiano individuato da s e non
contenente r. Se congiungiamo T con qualsiasi punto R sulla retta r il segmento TR deve
intersecare la retta s in un punto: S infatti tale segmento congiunge punti in semipiani opposti
rispetto ad s.
1
T
P
t
M
S
s
r
R
Sia ora M uno qualsiasi degli infiniti punti interni al segmento ST e consideriamo la retta w
supporto di ST.
Notiamo che w è distinta da s e da t, perché passa per il punto M che non appartiene né a s né
a t e distinti punti interni a ST individuano distinte rette.
Allora w non interseca r. Infatti se la intersecasse in un punto R’ sulla semiretta di origine P e
contenente M, allora avremmo un triangolo MRR’ il cui lato MR è attraversato dalla retta s in un
punto interno e quindi per l’assioma di Pasch la retta s dovrebbe attraversare anche un altro
lato. Ma s non può attraversare MR’, altrimenti s e w coinciderebbero, avendo due punti in
comune. Quindi s attraverserebbe il lato RR’ e quindi intersecherebbe r contro l’ipotesi.
T
P
t
M
w
S
s
r
R
R’
w
Se invece w intersecasse r in un punto R” sulla semiretta di origine P opposta a M allora a M
allora questa volta sarebbe la retta t ad entrare nel triangolo RMR” attraverso un punto interno
del lato MR” e si conclude analogamente a prima, perché t passerebbe per il lato RR” e quindi
intersecherebbe r.
w
T
P
t
M
w
S
s
R”
R
r
w
2
3. Proposizione. Se vale assioma di Lobatchevski forma debole per una retta ed un punto
fuori di essa, allora vale per ogni altra retta ed ogni altro punto fuori di essa.
Dim. Infatti se esistessero una retta s ed un punto R fuori di essa tali che per R passasse
un’unica retta s’ non intersecante s consideriamo allora la perpendicolare RS condotta da R alla
retta s e consideriamo su s anche un altro punto S’ diverso da s. L’angolo SS’R è congruente
all’angolo S’RA, dove A è un opportuno punto della retta s’ in modo tale che con il precedente
si formi una coppia di angoli alterni interni tra la trasversale S’R e le rette s ed s’. Infatti se
così non fosse, sarebbe possibile tracciare per R un'altra retta s”, distinta da s’, formante con
RS’ un angolo congruente a SS’R, allora anche s” ed s non si intersecherebbero, come previsto
dalla proposizione I.27 degli Elementi di Euclide (che è un teorema nella geometria assoluta)
A
R
s’
s”
S’
S
B
s
Un’analoga considerazione porta a concludere che l’angolo SRQ sarebbe retto, come il suo
alterno interno BQR. Torniamo ora al triangolo rettangolo S’SR: per quanto appena visto la
somma dei suo angoli interni varrebbe allora due angoli retti, risultato che come abbiamo già
visto è equivalente al quinto postulato.
4. Osservazione. La dimostrazione della proposizione 2 prova anche fatto seguente:
siano r una retta e P un punto esterno ad essa e sia H il piede della perpendicolare condotta da
P ad r. Se s e t sono due rette per P che non intersecano r e formano con PH e dalla stessa
parte due angoli ,
, con < , allora nessun’altra retta uscente da P e formante con PH e
dalla medesima parte un angolo compreso fra e , incontra r.
5. Osservazione. Consideriamo ancora una retta siano r una retta e P un punto esterno ad
essa e sia H il piede della perpendicolare condotta da P ad r. Consideriamo per la retta s per P
e perpendicolare a PH. Le rette r ed s non si intersecano (ad esempio perché formano angoli
alterni interni congruenti). Sia poi K un punto di s da una delle due parti (a destra nel disegno)
rispetto a P. Consideriamo ora le rette del fascio per P, che passano internamente all’angolo
HPK. Tali rette possono essere ripartite in due classi contigue, contenenti la prima classe tutte
le rette che incontrano la retta r, e la seconda tutte le rette che non incontrano la retta r.
P
K
’
s
T’
t’
H
r
3
Poiché si ammette l’assioma di continuità, la ripartizione definisce una retta t’, elemento
separatore delle due classi, la quale gode delle seguenti proprietà:
1) t’ non incontra la retta r
2) detto ’ := ∢HPT’, l’angolo che t’ forma con PH nel semipiano fissato è: 0 < ’ < /2
3) ogni semiretta per P interna all’angolo ’ incontra la retta r, ogni semiretta per P esterna
all’angolo ’ interna all’angolo T’PK non incontra la retta r.
Infatti basta considerare gli angoli che le semirette per P interne all’angolo HPK formano con la
semiretta PH, e in corrispondenza poi alle semirette che non intersecano la r, prendere
l’estremo inferiore ’ dell’insieme di tali angoli (esiste per l’assioma di continuità).
Risulta allora ’ > 0, poiché ’ è maggiore dell’angolo HPM che si ottiene prendendo un punto
M della retta r nel semipiano fissato, dunque è: 0 < HPM < ’. Inoltre è ’ < /2, altrimenti la
retta s sarebbe la sola retta per P che non incontra la retta r. Si noti che ’ è anche l’estremo
superiore degli angoli formati dalle rette per P, che invece intersecano r.
6. Proposizione. La retta t’, introdotta nell’osservazione precedente, non incontra la retta r,
ossia appartiene alla seconda delle due classi.
Dim. Infatti se la intersecasse in un punto R, allora basterebbe prendere un punto M su r,
esterno al segmento HR dalla parte di R, e la retta supporto di PR intersecherebbe la retta r
pur formando con PH un angolo superiore a ’
P
s
’
t’
H
r
R
M
contro le proprietà di ’ come estremo superiore.
7. Osservazione. Gli argomenti sviluppati in uno dei due semipiani individuati da PH possono
essere ripetuti anche nell’altro semipiano e ciò consente di trovare una retta t” ed un angolo ”
aventi le stesso proprietà di t’ e di ’. Considerazioni di simmetria portano a concludere che
come angoli non orientati ’ = ”. Le due rette risultano simmetriche rispetto all’asse PH.
P
”
’
t”
t’
H
4
8. Definizione. Entrambe le rette t’ e t” si dicono rette parallele alla retta r per il punto P, ma
ciascuna relativamente ad uno dei due possibili versi di r. L’angolo non orientato ’ = ” (0,
/2) viene detto angolo di parallelismo della coppia (P, r). Le altre rette per P che non
intersecano r si dicono iperparallele (o ultraparallele o divergenti).
9. Osservazioni. a) Le parallele ad una retta data ed uscenti da un punto sono così due: una
per ciascuno dei versi della retta. Continua quindi a sussistere allora l’unicità della parallela
passante da un punto esterno da un punto esterno alla retta, ma solo relativamente ad un
verso fissato della retta.
b) Senza postulare né il quinto postulato, né la sua negazione (ossia nella geometria assoluta)
può essere definito l’angolo di parallelismo di una coppia (P, r), di ampiezza in (0, /2].
L’angolo di /2 corrisponde al caso euclideo e comporta la coincidenza delle due
nei due distinti versi in un’unica retta.
c) Ogni semiretta uscente dal punto esterno ad una retta data e contenuta
parallelismo interseca la retta ed il risultato continua a valere anche in
apparentemente più generale, ma equivalente ad esso, a cui ci riferiremo spesso
rette parallele
nell’angolo di
una versione
nel seguito:
siano r una retta, P un punto fuori da essa e t l’unica retta passante per P e parallela ad r in un
verso fissato, preso un punto R su r ed un punto T su t che segue P nel verso del parallelismo
(a destra nel disegno), allora ogni semiretta uscente da P ed interna all’angolo RPT interseca r.
P
T
t
R
r
d) La definizione di parallelismo va ulteriormente indagata in almeno due direzioni che
comportano in un certo senso la possibilità di svincolare da un particolare punto il parallelismo
di una retta nei confronti di un’altra relativamente ad un verso e la possibilità di re ndere
invertire il ruolo delle due rette e quindi di poter parlare di rette parallele fra di loro in un
determinato verso, come precisato nelle proposizioni 10 e 12.
10. Proposizione. Se s è la parallela condotta da un punto P ad una retta data r in un verso
assegnato, e Q è un punto qualunque di s, la parallela condotta per Q alla r, nel verso
considerato coincide con s.
Dim. Distinguiamo due casi.
Q segue P nel verso considerato (a destra nel disegno).
Indichiamo con H il piede della perpendicolare abbassata da P sul r, e congiunto Q con H, sia
QC una qualunque semiretta interna all’angolo PQS con S ulteriore punto di s che segue anche
Q nel verso considerato
5
s
P
Q
S
C
r
H
Tale semiretta interseca r. Infatti il risultato è vero se QC sono in semipiani opposti rispetto a
r. Altrimenti se, come nel disegno, sono dalla stessa parte basta considerare la semiretta di
origine P passante per C, questa essendo interna all’angolo HPS, angolo di parallelismo, deve
intersecare r in un punto D ed essendo interna al triangolo PHQ deve passare per un punto
interno E del lato HQ.
P
Q
S
s
E
C
r
H
D
Allora la semiretta QC ha un punto in comune C col lato ED del triangolo EDH quindi , per
l’assioma di Pasch, deve passare per un punto di un altro lato. Questo non può essere EH,
altrimenti la semiretta QC conterrebbe il lato EH, avendo due punti comuni col suo supporto e
quindi passa per un punto del lato HQ ed allora interseca r. Dati che ciò vale per ogni semiretta
uscente da Q ed interna all’angolo HQS mentre non vale per la semiretta estrema QS, s è la
retta per Q parallela ad r nel verso considerato.
Q precede P nel verso considerato.
Prendiamo ora la semiretta QC interna all’angolo HQP ed un punto D sul suo prolungamento
nel verso opposto tale retta entra nel triangolo HQP quindi passa per un punto F del lato PH. La
retta DP passa internamente all’angolo HPS (angolo di parallelismo) e quindi interseca r in un
punto E. La retta QC entra ora nel triangolo HPE attraverso il lato PH non può uscire da esso
attraverso il lato PE altrimenti le rette QC e PE coinciderebbero, mentre hanno il solo punto D
in comune ed allora QC interseca il lato HE e quindi la retta r.
D
Q
P
S
s
F
C
H
E
6
r
Si conclude come nel caso precedente.
11. Osservazione. Se una retta r è parallela ad una retta in un dato verso, allora le due rette
non hanno nessuna perpendicolare comune. Infatti la perpendicolare condotta da un qualsiasi
punto di r ad s, individua con r l’angolo di parallelismo relativo a quel punto che è acuto.
12. Proposizione (simmetria o reciprocità del parallelismo) Se r è parallela a s, allora s è
parallela ad r (in un verso assegnato).
Dim. Sia r una retta parallela ad una retta s in un verso assegnato (a destra nel disegno) e
fissiamo dei punti A, R su r e B, S su s con R, S oltre A e B nel verso del parallelismo. Le due
bisettrici interne agli angoli BAR e ABS si intersecano in un punto M: infatti dato che s è
parallela ad r allora la bisettrice uscente da A deve intersecare r in quanto forma un angolo
minore dell’angolo di parallelismo e così la bisettrice uscente da B entra in un triangolo e deve
quindi intersecare il lato opposto supportato dall’altra bisettrice
A
R
r
M
B
S
s
Da M conduciamo le tre perpendicolari MH, MK, ML ai lati BS, AR, AB. Per la proprietà di
equidistanza della bisettrice dai lati dell’angolo risulta MH ML MK. Notiamo che i punti HMK
non sono allineati, infatti se lo fossero HK sarebbe una perpendicolare comune alle rette r e s,
ma r è parallela e quindi ciò è impossibile per l’osservazione 11.
A
K
R
L
r
M
B
H
S
s
Sia ora HX una semiretta uscente da H internamente all’angolo HKS; è sufficiente dimostrare
che tale semiretta interseca r: infatti il fatto che r ed s non si intersecano comporta allora che s
sia parallela ad r. Notiamo anche che gli angoli KHS e HKR sono congruenti in quanto
differenza di angoli congruenti: gli angoli retti MBS e MKR meno gli angoli congruenti MHK e
MKH angoli alla base di un triangolo isoscele. Facciamo uscire da K una semiretta interna
all’angolo HKR e formante con HK un angolo congruente a XHK. Tale semiretta deve
intersecare la retta s in un punto E in quanto risulta interna all’angolo di parallelismo fra r ed s.
Preso poi un punto F su r oltre K nel verso del parallelismo con HF EK i triangoli KHE e HKF
risultano congruenti per LAL. In particolare l’angolo FHK è congruente all’angolo EKH il quale è
7
congruente a XHK e quindi la semiretta HX contiene il lato HF e perciò interseca r esattamente
in F.
A
K
F
R
M
B
r
X
H
E
S
s
13. Proposizione (transitività del parallelismo). Due rette parallele ad una terza in un
determinato verso sono parallele fra loro nello stesso verso.
Dim. Siano r, s rette parallele alla stessa retta t nel medesimo verso (nel disegno a destra) e
distinguiamo due casi.
Se r e s sono in semipiani opposti rispetto a t, prendiamo due punti R, S sulle rette r, s. Il
segmento RS interseca t in un punto T prendiamo poi degli ulteriori punti R’, S’ sulle stesse
rette r, s, che seguono i punti precedenti nel verso del parallelismo. Consideriamo una
semiretta uscente da S ed interno all’angolo RSS’. Poiché è interna all’angolo di parallelismo
essa deve intersecare la retta T in un punto M, la stessa semiretta, uscendo da M, è interna
all’angolo RMT’ dove T’ è un punto su t che segue M nel verso del parallelismo. Quindi la
semiretta interseca anche r in un punto N. Dato che ciò si verifica con ogni semiretta uscente
da S ed interna all’angolo RSS’ e non con la semiretta SS’, ne risulta il parallelismo fra r ed s
S
s
S’
M
t
T
T’
R
N
R’
r
Se invece r e s sono nello stesso semipiano individuato da t, allora non possono incontrarsi
perché altrimenti dallo stesso punto uscirebbero due distinte rette parallele nello stesso verso.
Ora una delle due rette r o s lascerà in semipiani opposti le altre due e con un ragionamento
analogo si ha il risultato voluto.
14. Osservazioni-Definizioni (elementi impropri). Il sistema di tutte le rette del piano
parallele in un determinato verso ad una retta assegnata sullo stesso piano, gode di due
proprietà: 1) per un punto del piano passa una ed una sola retta del sistema; 2) due rette
qualunque del sistema lo individuano completamente.
Queste proprietà appartengono anche al fascio di rette per un punto, dunque estendendo il
significato della parola fascio, si parlerà di fascio (improprio) di rette parallele.
8
Tutte le rette di un fascio proprio hanno in comune un punto, detto il centro del fascio. Le rette
di un fascio improprio hanno in comune il verso di parallelismo. Un punto improprio (o ideale)
è allora il verso comune delle rette di un fascio improprio; tale punto improprio, comune a
tutte le rette del fascio, verrà ancora detto centro del fascio e sarà indicato con una lettera
maiuscole dell’alfabeto greco. Una retta è completamente individuata anche da un suo punto
proprio P e da un punto improprio , per l’unicità della parallela per un punto in un
determinato verso ad una retta assegnata. La retta P indicherà la retta passante per il punto
proprio P ed avente il punto improprio , le rette P e Q indicheranno due rette passanti per i
punti P e Q rispettivamente e parallele tra di loro relativamente al loro punto improprio
comune .
15. Proposizione. La somma degli angoli coniugati interni formati da una trasversale con due
parallele nel verso comune di parallelismo è minore di due angoli retti.
Dim. Siano P e Q due rette parallele e sia M il punto medio del segmento PQ. Da P
conduciamo le perpendicolari P’ e Q’ alle rette P e Q.
P
P’
M
Q’
Q
Se la somma degli angoli PQ e QP fosse di due angoli retti, allora gli angoli P’PM e Q’QM
risulterebbero congruenti e quindi tal sarebbero anche i triangoli rettangoli (con ipotenuse
congruenti) P’PM e Q’QM, quindi sarebbero congruenti anche gli angoli in M dei due triangoli e
pertanto, essendo i punti P, M, Q allineati, lo sarebbero anche P’, M, Q’ e quindi le rette
parallele P e Q avrebbero una perpendicolare comune contro l’osservazione 11. Se invece la
somma degli angoli fosse maggiore di due angoli retti allora potremmo considerare una
semiretta P’ uscente da P e formante con PQ un angolo QP’ la cui somma con PQ sarebbe
uguale a due angoli retti e quindi P’ sarebbe interna all’angolo di parallelismo (osservazione 9
(c)) e quindi intersecherebbe Q. Ma, come prima, si avrebbe che le perpendicolari condotte
da M alle rette Q e P’ sarebbero allineate e quindi Q e P’ avrebbero una perpendicolare
comune, ma rette che si intersecano non hanno perpendicolari comuni nemmeno nella
geometria assoluta.
16. Osservazione. Nella corso della dimostrazione precedente abbiamo visto un risultato, che
può essere così generalizzato (verificare i dettagli):
due rette che formano con una trasversale angoli coniugati supplementari, o alterni interni
congruenti o corrispondenti congruenti non si intersecano nella geometria assoluta e sono
iperparallele nella geometria iperbolica.
9
17. Proposizione. Le distanze fra i punti di due rette parallele decrescono procedendo sulle
rette nel verso del parallelismo.
Dim. Siano r, s due rette parallele nel verso comune e siano R, R’ due punti di r che si
succedono nel verso e prendiamo su s i punti S, S’, piedi delle perpendicolari da essi
condotte su s. Se RS fosse congruente a R’S’, allora ne risulterebbe che l’asse del segmento
SS’ sarebbe perpendicolare a RR’ e questo fatto è impossibile per l’osservazione 11. Infatti sia
HK l’asse del segmento SS’ con K punto del segmento RR’. I triangoli RSH e R’S’H sarebbero
congruenti per LAL e quindi per LAL sarebbero congruenti i triangoli RHK e R’HK: infatti per la
congruenza dei triangoli precedenti, sarebbero congruenti i lati RH e RH’ e gli angoli RHK e
R’HK (in quanto differenze di angoli congruenti).
R
K
R’
S
H
S’
Se invece RS fosse minore di R’S’, allora prendendo un punto R” interno al segmento R’S’ e
tale che R”S’ sia congruente a RS, la semiretta uscente da R, RR” allora intersecherebbe S
(per l’osservazione 9 (c)), mentre, argomentando come sopra, l’asse di SS’ sarebbe
perpendicolare a RR” e ciò è impossibile perché l’esistenza di una perpendicolare comune
impone che due rette non si intersechino.
R
R’
R”
S
H
S’
18. Osservazione. Si potrebbe dimostrare un risultato più preciso:
la distanza di un punto variabile su una delle due rette parallele dall’altra è una funzione
continua dell’ascissa del punto, che tende a zero quando l’ascissa tende all’infinito nel verso del
parallelismo, diverge a + ∞ nel verso opposto.
19. Definizioni. Date due rette parallelo r, s nel verso comune di parallelismo , la striscia di
lati r, s è la parte di piano formata dai punti di r e di s e dai punti che si trovano, rispetto a
ciascun lato, nel semipiano contenente anche l’altro lato.
Presi poi due punti R, S sulle rette r ed s rispettivamente diremo trilatero (o triangolo aperto)
la figura formata dal segmento RS e da quella parte della striscia limitata da AB e
dalle semirette R e S. RS, R, S si dicono i lati del trilatero.
10
R
S
20. Osservazione. Due trilateri RS, R’S’’ sono congruenti se hanno congruenti i lati RS,
R’S’, la coppia di angoli RS, R’S’’ e la coppia di angoli SR, S’R’’. Vale di più la seguente
21. Proposizione (criterio di congruenza fra i trilateri). Due trilateri RS, R’S’’ cono
congruenti se sono congruenti i lati RS, R’S’ ed una delle due coppie di angoli.
Dim. Per fissare le idee supponiamo che siano congruenti gli angoli SR, S’R’’. Se gli angoli
dell’altra copia non fossero congruenti, ad esempio RS < R’S’’, allora sarebbe possibile fare
uscire dal vertice S’ una semiretta interna all’angolo R’S’’ e formante con R’S’ un angolo
congruente a RS. Tale semiretta dovrebbe incontrare allora R’’ in un punto T’. Preso poi un
punto T sulla semiretta R tale che i segmenti RT ed R’T’ siano congruenti.
R
T
_
S
R’
T’
’
_
S’
Allora i triangoli SRT e S’R’T’ risulterebbero congruenti per LAL (attorno agli angoli in R ed R’)
da cui per congruenza degli angoli RS e R’S’T’ anche R ed S dovrebbero intersecarsi in T.
22. Proposizione (teorema dell’angolo esterno per trilateri). In ogni trilatero ciascun angolo
esterno è maggiore dell’angolo interno non adiacente.
Dim. Sia RS un trilatero e sia T un punto allineato con R e S esterno al segmento RS dalla
parte di R. Si ha ∢SR + ∢TR = due angoli retti, mentre per la proposizione 15 ∢SR +
∢RS < due angoli retti, sottraendo le due relazioni si ottiene: ∢TR > ∢RS
11
T
R
S
23. Proposizione. L’angolo di parallelismo della parallela ad una retta r da un punto P esterno
ad essa è funzione solo della distanza di P dalla retta r ed è funzione decrescente della
distanza.
Dim. Infatti se P’ è un altro punto distante da un’altra retta r’ come P da r consideriamo le
parallele per P e P’ alle rette r ed r’ nei versi ed ’. Presi H ed H’ i piedi delle perpendicolari
condotte da P ad r e da P’ ad r’ rispettivamente allora i trilateri PH e P’H’’ sono congruenti in
quanto sono congruenti i lati PH e P’H e gli angoli (retti) PH e P’H’’.
P
H’
P’
|
_
H
’
Grazie alla proposizione 21 possiamo concludere che gli angoli di parallelismo sono congruenti.
Sia ora r una retta e sulla perpendicolare per un suo punto O prendiamo due punti P e Q sulla
stessa semiretta per O con P interno a OQ. Da P e da Q mandiamo le due parallele ad r nello
stesso verso .
Q
P
O
Gli angoli di parallelismo OP e OQ sono angolo esterno ed interno non adiacente del trilatero
PQ, quindi OP > OQ per la proposizione 22.
12
23. Osservazione. Si potrebbe dimostrare in modo più preciso e meno banale che
l’angolo di parallelismo è una funzione continua della distanza fra il punto e la retta che
/2 e quindi (poiché è decrescente) tende a /2 quando la distanza
tende a 0 e tende a 0 quando la distanza tende a + .
assume tutti i valori tra 0 e
È la relazione tra le grandezze angolari e lineari, determinata dalla funzione α = Π (x) che
definisce il carattere eminentemente originale della geometria iperbolica. La similitudine delle
figure, ad esempio, non esiste in tale geometria, poiché le grandezze angolari e le grandezze
lineari sono legate tra loro da equazioni, dunque definire tutti gli angoli di un triangolo implica
la definizione di tutti i suoi lati, così che due triangoli aventi gli angoli ordinatamente
congruenti, hanno congruenti anche i lati.
Un’altra particolarità della geometria iperbolica è legata alla scelta dell’unità di misura della
lunghezza. In geometria euclidea si trovano delle costanti angolari assolute, vale a dire degli
angoli la cui costruzione si presta ad una descrizione astratta (senza che sia necessario
attribuire un contenuto concreto agli enti geometrici); l’arbitrarietà ammessa nella costruzione
non influisce sulla grandezza degli angoli ottenuti, vale a dire che essi risultano congruenti tra
loro. A titolo di esempio è sufficiente citare l’angolo retto. Se si adotta l’angolo retto come
unità degli angoli, tutte le misure divengono possibili senza che sia necessario un “campione”
di angolo retto, prestandosi questo ogni volta ad una costruzione precisa, al contrario, le
costanti lineari assolute non esistono in geometria euclidea. Per poter esprimere la lunghezza
di un segmento per mezzo di una quantità, siamo obbligati ad avere una unità di lunghezza
convenzionale sotto forma di un segmento arbitrario. Non si può descrivere il segmento scelto:
per confrontarlo con altri segmenti bisogna mostrare il suo campione. In pratica, per la misura
delle lunghezze, si utilizzano delle copie del metro campione, la scelta del quale non è soggetta
ad alcun imperativo geometrico. La geometria di iperbolica prevede, al contrario, a fianco delle
costanti angolari assolute, anche delle costanti lineari assolute. Così dunque un segmento il cui
angolo di parallelismo associato, sia /4 è definito nella misura in cui la funzione “angolo di
parallelismo” è definita. Abbiamo visto che questa funzione è completamente definita per ogni
valore positivo, per la proprietà del piano iperbolico, vale a dire per la proprietà della varietà
degli enti geometrici descritti dagli assiomi della geometria iperbolica.
24. Proposizione. Il quarto angolo di ogni quadrilatero trirettangolo è acuto.
Dim. Sia ABCD un quadrilatero trirettangolo, rettangolo in A, B, D Prolunghiamo i lati CD e BA
dalle parti di A e di D e prendiamo i punti B’ e C’ tali che D’A AB e C’D DC.
C’
D
C
B’
A
B
I triangoli ACD e AC’D’ sono congruenti per LAL e quindi per lo stesso criterio lo sono i triangoli
ABC e AB’C’. Quindi B’C’ è congruente a BC e anche l’angolo AB’C’ è retto.
Conduciamo ora le parallele per C e C’ alla retta BB’ nel verso da B’ a B e sia il loro punto
improprio. Sia X un punto sul prolungamento di DC.
13
C’
D
C
X
B’
A
B
Si ha allora ∢XC > ∢CC’, poiché XC angolo esterno del trilatero CC’, ed inoltre ∢B’C’ =
∢BC, in quanto angoli di parallelismo relativi alla stessa distanza (proposizione 23). Pertanto
∢BCD = ∢B’C’D < ∢BCX e dato che la somma degli angoli BCD e BCX vale due angoli retti
ne segue che ∢BCD è acuto.
25. Corollario. Ogni quadrilatero birettangolo isoscele ha due angoli acuti.
26. Osservazione. Nella dimostrazione della proposizione 24 avremmo potuto ricondurci ad
un quadrilatero birettangolo isoscele (dove esattamente?) e concludere con il risultato che
abbiamo visto a suo tempo essere valido in quel caso, ma abbiamo seguito una strada
autonoma per dimostrare la proposizione sul quadrilatero trirettangolo. Dopo averla
dimostrata, è possibile enunciare come corollario l’analogo risultato per l’altro quadrilatero,
invitando ad esplicitare i dettagli della dimostrazione.
Nel seguito di queste note esamineremo alcune proprietà delle rette divergenti cominciando da
un paio di risultati che in realtà abbiamo già visto nelle pagine precedenti. Li riportiamo qui per
completezza invitando ad esplicitare nuovamente le dimostrazioni.
27. Proposizione. Due rette perpendicolari ad una terza sono divergenti.
28. Proposizione. Due rette che formano angoli alterni o corrispondenti uguali con una
secante sono divergenti.
29. Proposizione. Due rette divergenti hanno una ed una sola perpendicolare comune.
Dim. L’unicità segue dal risultato sul quadrilatero trirettangolo: infatti due distinte
perpendicolari individuerebbero un quadrilatero con quattro angoli retti.
Siano ora a e b due rette divergenti A e A1 due punti su a e B e B1 i piedi delle perpendicolari
per quei punti alla b. Se fosse AB A1B1 l’asse del segmento BB1 sarebbe la perpendicolare
cercata (ricordare quanto visto nel caso del quadrilatero di Saccheri)
a
A1
A
b
B1
B
14
Altrimenti uno dei due è maggiore dell’altro: diciamo A1B1 > AB.
Indichiamo con il punto improprio della semiretta di origine A1 e passate per A. Su B1A1
prendiamo un segmento B1A’ BA e per A’ si mandiamo dalla parte di il raggio A’’ formante
con A’B1 un angolo congruente a BA. Poi congiungiamo i punti impropri , ’ con B e B1
rispettivamente.
A1
A
A’
’ _
_
’
*
B1
*
B
I due trilateri AB, A’B1’ sono congruenti poiché A’B’ e AB sono congruenti e così anche gli
angoli in A e in A’. Ne segue la congruenza fra gli angoli AB e A’B1’. Dunque B e B1’ sono
divergenti poiché formano angoli corrispondenti * congruenti con la trasversale B1B. Allora
anche A’’ e B sono non secanti poiché stanno da parti opposte rispetto alla B 1’.
Ciò posto è facile dimostrare anche che A’’ e A si incontrano. Infatti la retta A’’ se non
interseca il lato A1A del quadrilatero A1B1BA (nel qual caso avremmo che A’’ e A si
incontrerebbero) incontrerà il lato AB del trilatero AB, e poiché non incontra il lato B,
incontrerà necessariamente il terzo lato, cioè A, infatti altrimenti si avrebbe = ’ e quindi
B e B1’ sarebbero parallele invece che divergenti. Indichiamo con M’ il punto comune ad A
e A’’ e P’ il piede della perpendicolare calata da M’ su b. Sulla semiretta A prendiamo il
segmento AM A1M’ e sia P il piede della perpendicolare condotta da M a b.
A1
A
A’
M’
’
M
B1
B
P’
P
I due quadrilateri AMPB, A1M’P’B1 sono congruenti (perché?) da cui MP M’P’. Allora il
quadrilatero P’PMM’ è birettangolo isoscele sulla base P’P e quindi, come noto, l’asse della base
P’P è perpendicolare anche ad MM’.
30. Osservazione-definizione. Data una retta le rette perpendicolari ad essa (ce n’è una ed
una sola per ogni punto della retta) sono tutte divergenti fra loro e costituiscono ancora una
ulteriore tipo di fascio: il fascio (improprio) delle rette (divergenti) ortogonali ad una retta
data.
15
31. Proposizione. Date due rette divergenti, la distanza da una di esse di un punto P
dall’altra aumenta quando P si allontana dal piede della perpendicolare comune. La
perpendicolare comune dunque dà la minima distanza tra due divergenti.
Dim. Consideriamo due rette divergenti a e b, con AB la loro perpendicolare comune. Da un
altro punto P su b abbassiamo la perpendicolare PC su a. Prendiamo sulla semiretta di origine
C che contiene P il punto E tale che CE sia congruente ad AB. Allora ACEB è un quadrilatero
birettangolo isoscele sulla base AC quindi gli altri angoli in B ed in E sono acuti e pertanto
l’angolo in B è contenuto nell’angolo retto ABP ed il punto E è interno al segmento CP, dunque
AB CE < CP.
P
B
E
_
_
A
C
Preso ora un altro punto P’ sulla semiretta di origine B passante per P in modo che BP < BP’, e
indicata con C’ la sua proiezione ortogonale sulla retta a, indichiamo con E’ un punto sulla
semiretta C’ P’ tale che E’C’ PC, si trova analogamente CP < C’P’. Infatti l’angolo E’PC è acuto
(il quadrilatero CC’E’P è birettangolo isoscele sulla base CC’), mentre CPP’ è ottuso (infatti è
acuto l’angolo CPB: quarto angolo del quadrilatero trirettangolo BACP), quindi l’angolo CPE’ è
contenuto nell’angolo CPP’ ed il punto E’ è interno al segmento C’P.
B
P
P’
E’
E
_
_
A
C
C’
Dunque, allontanandosi da B, la distanza tra le due rette aumenta.
32. Osservazione. Si potrebbe anche dimostrare che:
la distanza tra due rette divergenti tende a + ∞ quando il punto P si allontana dal piede della
perpendicolare comune, cioè si può trovare per ogni numero m positivo un punto P sulla b,
dall’una e dall’altra parte della perpendicolare comune, che ha distanza da a maggiore di m.
Ed anche che:
le proiezioni dei punti di una delle due rette divergenti sull’altra coprono solo un segmento di
lunghezza finita sulla seconda retta. Esistono cioè due punti, C 1 e C2 sulla a, simmetrici rispetto
al piede H della perpendicolare comune, per i quali, e oltre i quali, ogni perpendicolare alla a
non interseca la b.
16