Funzioni elementari (e funzioni definite a tratti notevoli)

Funzioni elementari
1 Funzioni elementari . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 1
1.1. Potenze ad esponente naturale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .pag. 1
1.2. Potenze ad esponente intero negativo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 2
1.3. Potenze ad esponente razionale positivo non intero . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 2
1.4. Potenze ad esponente razionale negativo non intero . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 3
1.5. Potenze ad esponente irrazionale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 4
1.6. Funzioni esponenziali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 5
1.7. Funzioni logaritmiche. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .pag. 5
1.8. Funzioni trigonometriche . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 6
1.9. Funzioni trigonometriche inverse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 7
1.10. Funzioni iperboliche e loro inverse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 8
2 Funzioni definite a tratti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 9
2.1. Segnante . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 9
2.2. Valore assoluto . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 9
2.3. Parte intera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 10
2.4. Mantissa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . pag. 10
1. FUNZIONI ELEMENTARI
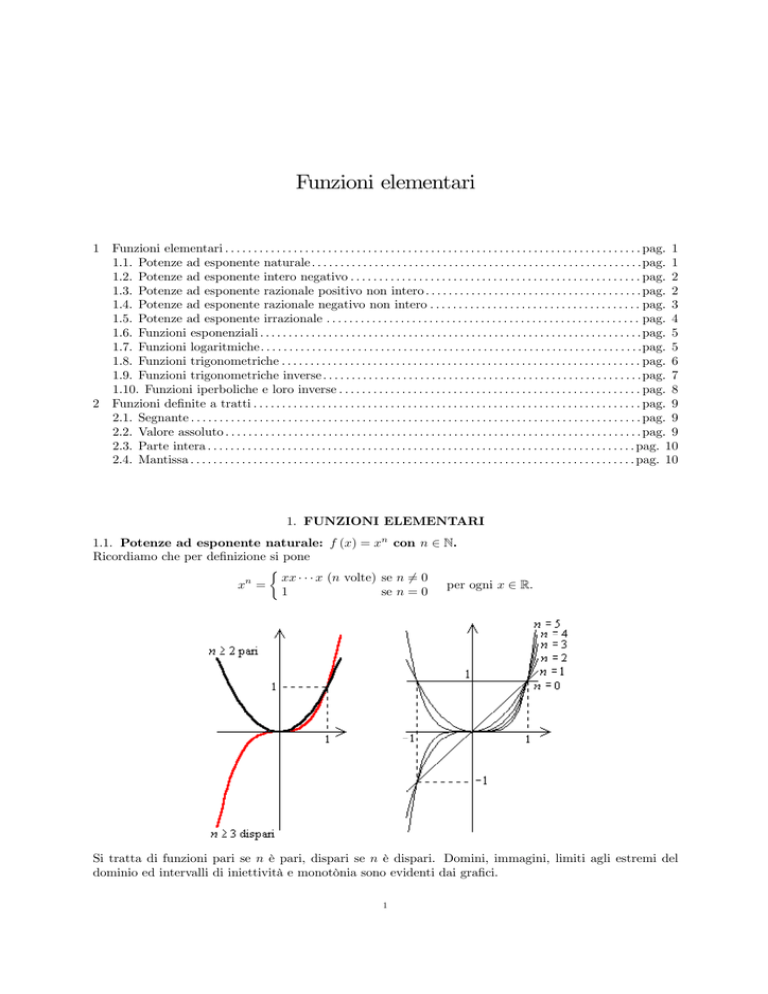
1.1. Potenze ad esponente naturale: f (x) = xn con n 5 N.
Ricordiamo che per definizione si pone
xx · · · x (n volte) se n 9= 0
per ogni x 5 R.
xn =
1
se n = 0
Si tratta di funzioni pari se n è pari, dispari se n è dispari. Domini, immagini, limiti agli estremi del
dominio ed intervalli di iniettività e monotònia sono evidenti dai grafici.
1
2
M .GUIDA, S.ROLANDO
1.2. Potenze ad esponente intero negativo: f (x) = xn con n 5 N .
Ricordiamo che per definizione si pone
xn =
1
xn
per ogni x 5 R, x 9= 0.
Sono funzioni pari se n è pari, dispari se n è dispari. Domini, immagini, limiti agli estremi del dominio
ed intervalli di iniettività e monotònia sono evidenti dai grafici.
m
1.3. Potenze ad esponente razionale positivo non intero: f (x) = x n con m, n 5 N primi tra
loro, n 9= 1.
Ricordiamo che per definizione si pone
m
xn =
s
n
xm
per ogni x 5 R tale che la radice abbia senso.
Occorre allora distinguere vari casi, sulla base della parità o disparità di m ed n.
m pari Si tratta di funzioni pari, con dom f = R.
FUNZIONI ELEM ENTARI
3
m dispari ed n dispari Si tratta di funzioni dispari, con dom f = R.
m dispari ed n pari Risulta dom f = [0, +4).
Immagini, limiti agli estremi del dominio ed intervalli di iniettività e monotònia sono evidenti dai grafici.
m
1.4. Potenze ad esponente razionale negativo non intero: f (x) = x n con m, n 5 N primi
tra loro, n 9= 1.
Ricordiamo che per definizione si pone
m
1
x n = s
n
xm
per ogni x 9= 0 tale che la radice abbia senso.
Occorre ancora distinguere vari casi, sulla base della parità o disparità di m ed n.
m pari Si tratta di funzioni pari, con dom f = R \ {0}.
4
M .GUIDA, S.ROLANDO
m dispari ed n dispari Si tratta di funzioni dispari, con dom f = R \ {0}.
m dispari ed n pari Risulta dom f = (0, +4).
Immagini, limiti agli estremi del dominio ed intervalli di iniettività e monotònia sono evidenti dai grafici.
1.5. Potenze ad esponente irrazionale: f (x) = x con 5 R \ Q.
La potenza x è definita tramite un procedimento di approssimazione mediante potenze ad esponente
razionale, che non richiamiamo. Risulta dom f = (0, +4) se < 0, dom f = [0, +4) se > 0.
Immagini, limiti ed intervalli di iniettività e monotònia sono evidenti dai grafici.
FUNZIONI ELEM ENTARI
5
1.6. Funzioni esponenziali: f (x) = ax con a 5 R, a > 0.
Risulta dom f = R in ogni caso e particolare rilevanza ha la base irrazionale e = 2.718281828459...
(numero di Nepero).
Immagini, limiti agli estremi del dominio ed intervalli di iniettività e monotònia sono evidenti dai grafici.
Valgono le seguenti proprietà:
1
• per ogni x 5 R si ha ax = x ;
a
• per ogni x, y 5 R si ha
ax
= axy e (ax )y = axy ;
ax ay = ax+y ,
ay
• per ogni x 5 R e b 5 R, b > 0 si ha
ax a x
ax bx = (ab)x e
=
.
bx
b
1.7. Funzioni logaritmiche: f (x) = loga x con a 5 R, a > 0, a 9= 1.
Sono le funzioni inverse delle funzioni esponenziali:
loga ax = x per ogni x 5 R,
aloga x = x per ogni x > 0.
Risulta dom f = (0, +4) in ogni caso. Immagini, limiti agli estremi del dominio ed intervalli di iniettività
e monotònia sono evidenti dai grafici.
Valgono le seguenti proprietà:
• loga x + loga y = loga (xy)
per ogni x, y > 0;
x
• loga x loga y = loga
per ogni x, y > 0;
y
6
M .GUIDA, S.ROLANDO
• loga (x ) = loga x per ogni x > 0 e 5 R;
logb x
• loga x =
per ogni x > 0 e b 5 R, b > 0, b 9= 1 (cambiamento di base).
logb a
1.8. Funzioni trigonometriche: sin x, cos x, tan x, cot x.
Le funzioni seno (dispari) e coseno (pari) sono definite per ogni x 5 R, tramite il procedimento geometrico
seguente: (cos x, sin x) sono le coordinate del punto P (x) che si rintraccia sulla circonferenza goniometrica
X 2 + Y 2 = 1, partendo dal punto (1, 0) e percorrendo un arco di lunghezza pari a |x|, in senso antiorario
se x 0, in senso orario se x < 0.
Si tratta di funzioni limitate e periodiche di periodo minimo 2: per ogni x 5 R si ha infatti
e
|sin x| 1 e
sin (x + 2) = sin x e
|cos x| 1
cos (x + 2) = cos x.
Immagini ed intervalli di iniettività e monotònia sono evidenti dai grafici.
Sono notevoli le seguenti identità:
FUNZIONI ELEM ENTARI
7
• cos2 x + sin2 x = 1 per ogni x 5 R;
• sin (x + y) = sin x cos y + cos x sin y per ogni x, y 5 R;
• cos (x + y) = cos x cos y sin x sin y per ogni x, y 5 R.
Le ultime due relazioni sono note come formule di addizione e da esse discendono numerose altre identità
di uso frequente, tra cui ad esempio le cosiddette formule di duplicazione, bisezione, prostaferesi e Werner.
Ci limitiamo qui a ricordare le seguenti formule di duplicazione: per ogni x 5 R risulta
cos (2x) = cos2 x sin2 x.
sin (2x) = 2 sin x cos x e
Vale inoltre la disuguaglianza
sin x |sin x| |x| cos x per ogni x 5 ,
.
2 2
Le funzioni tangente e cotangente sono definite da
tan x =
sin x
cos x
per ogni x 5 R tale che cos x 9= 0
cot x =
cos x
sin x
per ogni x 5 R tale che sin x 9= 0
e
e risultano dispari e periodiche di periodo minimo .
Immagini, limiti agli estremi del dominio ed intervalli di iniettività e monotònia sono evidenti dai grafici.
1.9. Funzioni trigonometriche inverse: arcsin x, arccos x, arctan x.
Le funzioni
x 5 2 , 2 :$ sin x 5 [1, 1] ,
x 5 [0, ] :$ cos x 5 [1, 1] ,
x 5 2 , 2 :$ tan x 5 R
sono iniettive (e suriettive sugli insiemi di arrivo indicati) e possono quindi essere invertite, ottenendo
rispettivamente le funzioni arcoseno (dispari), arcocoseno e arcotangente (dispari):
arcsin (sin x) = x per ogni x 5 2 , 2 , sin (arcsin x) = x per ogni x 5 [1, 1] ,
arccos (cos x) = x per ogni x 5 [0, ] ,
cos (arccos x) = x per ogni x 5 [1, 1] ,
arctan (tan x) = x per ogni x 5 2 , 2 , tan (arctan x) = x per ogni x 5 R.
8
M .GUIDA, S.ROLANDO
Immagini, limiti agli estremi del dominio ed intervalli di iniettività e monotònia sono evidenti dai grafici.
1.10. Funzioni iperboliche e loro inverse: sinh x, cosh x, tanh x.
Per ogni x 5 R, per definizione si pone
sinh x =
ex ex
,
2
cosh x =
ex + ex
,
2
tanh x =
sinh x
ex ex
.
= x
cosh x
e + ex
Seno e tangente iperbolici sono funzioni dispari, mentre il coseno iperbolico è pari. Segnaliamo inoltre le
seguenti identità:
• cosh2 x sinh2 x = 1 per ogni x 5 R;
• sinh (x + y) = sinh x cosh y + cosh x sinh y per ogni x, y 5 R;
FUNZIONI ELEM ENTARI
9
• cosh (x + y) = cosh x cosh y + sinh x sinh y per ogni x, y 5 R.
Immagini, limiti agli estremi del dominio ed intervalli di iniettività e monotònia sono evidenti dai grafici.
Le funzioni
x 5 R :$ sinh x 5 R,
x 5 [0, +4) :$ cosh x 5 [1, +4) ,
x 5 R :$ tanh x 5 (1, 1)
sono iniettive (e suriettive) e possono quindi essere invertite, ottenendo rispettivamente le funzioni
s
sinh1 x = log x + x2 + 1
per ogni x 5 R
s
cosh1 x = log x + x2 1
per ogni x 5 [1, +4)
1
1+x
tanh1 x = log
per ogni x 5 (1, 1)
2
1x
di cui omettiamo i grafici. Tali funzioni sono spesso chiamate settore seno iperbolico (sett sinh), settore
coseno iperbolico (sett cosh) e settore tangente iperbolica (sett tanh), rispettivamente.
2. FUNZIONI DEFINITE A TRATTI
2.1. Funzione segnante: f (x) = sgn (x).
Per definizione, si pone
;
? 1 se x > 0
0 se x = 0
sgn (x) =
=
1 se x < 0
per ogni x 5 R.
Osserviamo che lim sgn (x) = 1 9= 0 = sgn (0) e lim+ sgn (x) = 1 9= 0 = sgn (0).
x$0
x$0
2.2. Funzione valore assoluto: f (x) = |x|.
Per definizione, si pone
|x| =
x se x 0
x se x < 0
per ogni x 5 R.
Si osservi che risulta |x| = sgn (x) x per ogni x 5 R e sgn (x) =
x
per ogni x 9= 0.
|x|
10
M .GUIDA, S.ROLANDO
2.3. Funzione parte intera: y = [x].
Per definizione, la parte intera [x] di un qualunque x 5 R è il massimo intero che non supera x, ossia
;
...
A
A
A
A
2 se x 5 [2, 3)
A
A
A
A 1 se x 5 [1, 2)
A
A
?
0 se x 5 [0, 1)
per ogni x 5 R.
[x] = max {k 5 Z : k x} =
1
se x 5 [1, 0)
A
A
A
A
2 se x 5 [2, 1)
A
A
A
A
3 se x 5 [3, 2)
A
A
=
...
Osserviamo che
• se k 5 Z, allora lim [x] = k 1 9= k = [k] e lim+ [x] = k = [k] (continuità da destra in k);
x$k
x$k
• se x0 5 (k, k + 1) con k 5 Z, allora lim [x] = k = [x0 ] (continuità in x0 ).
x$x0
2.4. Funzione mantissa: y = M (x).
La mantissa M (x) di un qualunque x 5 R è definita da
M (x) = x [x]
da cui segue la decomposizione
x = [x] + M (x)
per ogni x 5 R.
Osserviamo che la funzione mantissa risulta limitata e periodica di periodo minimo 1. Inoltre
• se k 5 Z, allora lim M (x) = 1 9= 0 = M (k) e lim+ M (x) = 0 = M (k) (continuità da destra in k);
x$k
x$k
• se x0 5 (k, k + 1) con k 5 Z, allora lim M (x) = x0 k = M (x0 ) (continuità in x0 ).
x$x0