Funzione Valore Assoluto
PROPRIETÀ:
• |x| ≥ 0 , ∀x ∈ R
• |x| = 0 se e solo se x = 0
• |x1 · x2| = |x1| · |x2| , ∀ x1, x2 ∈ R
y
x |x |
• 1 = 1 , ∀ x1 , x2 ∈
x2 |x2|
1
O
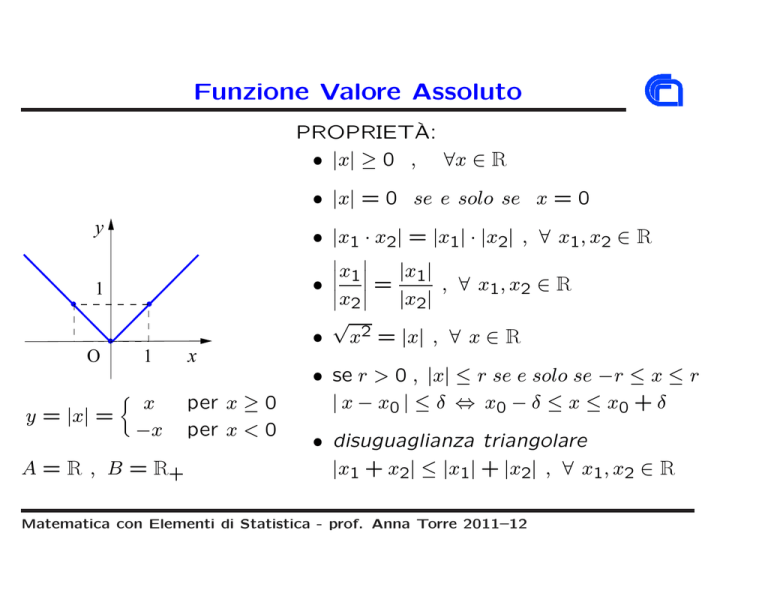
y = |x| =
1
x
−x
A = R , B = R+
x
per x ≥ 0
per x < 0
•
√
R
x2 = |x| , ∀ x ∈ R
• se r > 0 , |x| ≤ r se e solo se −r ≤ x ≤ r
| x − x0 | ≤ δ ⇔ x0 − δ ≤ x ≤ x0 + δ
• disuguaglianza triangolare
|x1 + x2| ≤ |x1| + |x2| , ∀ x1, x2 ∈ R
Matematica con Elementi di Statistica - prof. Anna Torre 2011–12
Funzioni Pari e Dispari
R
una funzione f :
R
→
R
si dice
• PARI:
se ∀x ∈ , f (−x) = f (x)
il grafico della funzione è simmetrico rispetto all’asse y
• DISPARI: se ∀x ∈ , f (−x) = −f (x)
il grafico della funzione è simmetrico rispetto all’origine O
• ESEMPI:
y = x2 , y = x2n ,
y = |x| , f unzioni pari
1
y = x , y = x2n+1 , y = , f unzioni dispari
x
R
y
y
y = f(x)
f(x)
y = f(x)
-x
f(x)
x
x
-x
O
x
O
- f(x)
x
Matematica con Elementi di Statistica - prof. Anna Torre 2011–12
Potenze ad esponente intero
y
y
x
O
O
y = x2
R → R+
x
f unzione pari
y = x3
R→R
f unzione dispari
• il grafico di xn è qualitativamente simile a quello di x2
quello di x3 se n è dispari.
Matematica con Elementi di Statistica - prof. Anna Torre 2011–12
se n è pari o a
Ancora Potenze
1
• POLINOMI: con operazioni di somma e prodotto si costruiscono polinomi, cioè
le funzioni del tipo:
x 7→ Pn(x) = a0 + a1 x + a2 x2 · · · an−1 xn−1 + an xn
polinomio di grado n.
• FUNZIONI RAZIONALI: facendo il quoziente di due polinomi P (x) e Q(x) si
ottengono le funzioni razionali del tipo:
R(x) =
P (x)
Q(x)
def inita su {x ∈
R / Q(x) 6= 0}.
• CASO PARTICOLARE: come caso particolare abbiamo le funzioni potenza
1
con esponente intero:
y = x−n = n def inita su
− {0}.
x
• POTENZE AD ESPONENTE RAZIONALE: per m ∈ − {0}, n ∈ − {0} e
x > 0 si definisce√la potenza ad esponente razionale come segue:
m
n
y = x n = xm .
• POTENZE AD ESPONENTE REALE: per estensione si può definire la potenza
ad esponente reale:
R
Z
y = xα
per ogni x > 0 e α ∈
R
N
resta indef inito 00 !!!.
Matematica con Elementi di Statistica - prof. Anna Torre 2011–12
Ancora Potenze
y
y
b>1
2
b=2
b<0
1
O
y = xb
0< b < 1
1
R+ → R+
x
per b > 0
1
O
y = xb
b=1/2
1
R+ → R+
PRODOTTO DI POTENZE DI ESPONENTE b :
se x, y, b ∈
R
con x > 0 e y > 0 , valgono le seguenti regole:
b
b
x
x
.
=
xb y b = (xy)b ,
yb
y
Matematica con Elementi di Statistica - prof. Anna Torre 2011–12
x
per b < 0
Funzione Esponenziale
y
y
1
1
O
y = ax
R → R+
x
con a > 1
• a0 = 1 , a1 = a
• ax > 0 , ∀x ∈
• x1 < x2 ⇒ ax1 < ax2 strettamente
crescente
• se x tende a +∞ ax tende a +∞
• se x tende a −∞ ax tende a 0
R
POPRIETÀ DELL’ESPONENZIALE:
axay = ax+y (prodotto) ,
O
y = ax
R → R+
x
con 0 < a < 1
• a0 = 1 , a1 = a
• ax > 0 , ∀x ∈
• x1 < x2 ⇒ ax1 > ax2 strettamente decrescente
• se x tende a +∞ ax tende a 0
• se x tende a −∞ ax tende a +∞
(ax )y = axy (composizione) ,
R
a−x =
Matematica con Elementi di Statistica - prof. Anna Torre 2011–12
1
(reciproco).
ax