RELAZIONE LINEARE: I MINIMI QUADRATI (cenni)
Spesso si ha a che fare con grandezze legate tra loro da una relazione lineare.
E possibile ricavare la relazione funzionale tra le grandezze tramite la misura
delle stesse.
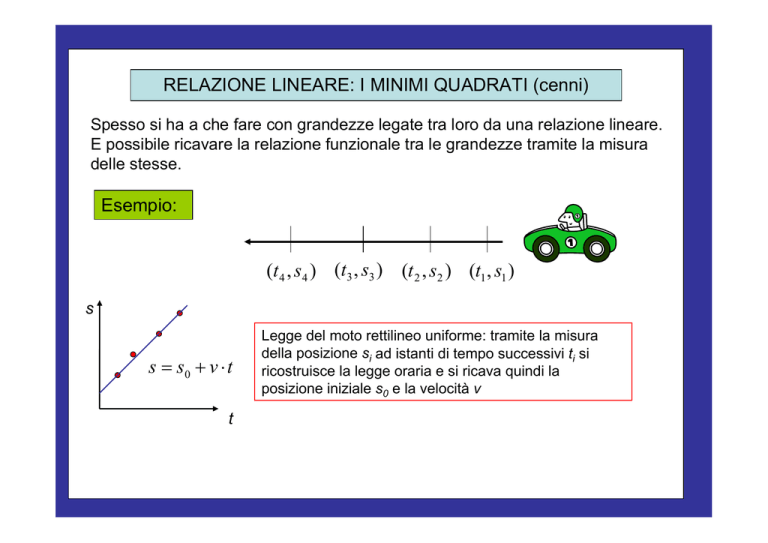
Esempio:
(t 4 , s4 ) (t3 , s3 ) (t 2 , s2 ) (t1 , s1 )
s
s s0 v t
t
Legge del moto rettilineo uniforme: tramite la misura
della posizione si ad istanti di tempo successivi ti si
ricostruisce la legge oraria e si ricava quindi la
posizione iniziale s0 e la velocità v
RELAZIONE LINEARE: I MINIMI QUADRATI (cenni)
Misurando le coppie di valori:
( xi , yi i )
dove in genere gli xi sono supposti con errore trascurabile, mentre agli yi
viene associato un errore sperimentali i
si vuole ricavare l’equazione della retta che meglio interpola (fitta) i
dati sperimentali.
In pratica considerata la retta:
Y=A+B·x
si vogliono ricavare i valori
(e i rispettivi errori) dei
parametri A e B
RELAZIONE LINEARE: I MINIMI QUADRATI (cenni)
Si dimostra che la miglior retta (e quindi i valori dei parametri della retta)
si ottiene andando a minimizzare la seguente quantità:
Chi-quadrato
RELAZIONE LINEARE: I MINIMI QUADRATI (cenni)
Si possono quindi ricavare delle formule per calcolare i parametri A e B
della retta, ed i rispettivi errori.
RELAZIONE LINEARE: I MINIMI QUADRATI (cenni)
Nel caso semplificato: i valori yi abbiano anch’essi errore trascurabile, o tutti
gli errori sono uguali tra loro, le formule si “riducono” a:
A
2
x
i yi xi yi xi
A
i
i
i
N xi2 xi
i
i
y2 xi2
i
N xi2 xi
i
i
B
i
2
2
B
N xi yi xi yi
i
i
i
N xi2 xi
i
i
2
N y2
N xi2 xi
i
i
2
Tali analisi vengono in genere affrontate mediante l’uso di opportuni software
di statistica, che forniscono i valori dei parametri, e dei loro errori, unitamente
a indici di bontà del fit
Test del chi quadrato (cenni)
Il fatto di avere delle formule o degli algoritmi che permettono di ricavare i
valori incogniti dei parametri non significa automaticamente che le misure
sperimentali sono in accordo con la relazione funzionale ipotizzata.
Un primo, banale test per verificare l’esistenza della relazione è mettere in
grafico i valori delle misure e confrontarli con la curva prevista (es. retta).
12
14
12
10
10
8
8
6
6
4
4
2
2
0
0
0
2
4
6
8
10
12
0
2
4
6
8
10
12
Test del chi quadrato (cenni)
Un metodo quantitativo è statisticamente corretto per verificare l’accordo
dei dati con una determinata relazione funzionale è il test del chi quadrato
Idealmente il numeratore (e quindi anche il chi quadrato) dovrebbe essere
uguale a zero (se tutti i punti giacessero sulla retta).
In realtà ci si aspetta che la differenza tra la misura (yi) e la previsione
(A+B·xi) sia dello stesso ordine di grandezza dell’error sperimentale i
pertanto ci si aspetta che ogni termine della sommatoria sia uguale a 1.
Di conseguenza è ragionevole aspettarsi che il chi quadrato sia circa uguale
al numero di misure effettuate (il numero cioè di addendi che sommo)
Test del chi quadrato (cenni)
Per generalizzare il discorso risulta quindi utile considerate il chi quadrato
ridotto, definito come rapporto tra il chi quadrato e il numero di gradi di libertà:
2
2
ng
Il numero di gradi di libertà ng lo possiamo considerare
come il numero di misure, meno il numero di parametri
ricavati a partire da tali misure
Il numero di gradi di libertà ng lo possiamo considerare come il numero di
misure, meno il numero di parametri ricavati a partire da tali misure
Di conseguenza è ragionevole aspettarsi che il chi quadrato ridotto sia poco
superiore a 1.
Anche per il chi quadrato (ridotto) esiste una funzione di densità di probabilità
(analogamente alla gaussiana) e, a partire da questa funzione è possibile
calcolare quanto vale la probabilità di trovare un certo valore di chi quadrato.
Test del chi quadrato (cenni)
Probabilità percentuale di trovare un valore di chi quadrato ridotto maggiore o
uguale a valori prefissati, in funzione del numero di gradi di libertà. Con tale
tabella si ricava quindi la probabilità che le misure fatte siano regolate dalla
relazione che era stata ipotizzata (ipotesi verificata se P>5%)
Test del chi quadrato (cenni)
In corrispondenza dei seguenti valori delle ascisse (tempo): 0s, 2s, 3s, 5s, sono misurati I seguenti
valori della variabile y (spazio =: -1.3 cm, 4.5 cm, 6.3 cm, 11.8 cm).
L’errore sulle x è trascurabile, quello sulle y è pari a 0.4 cm per tutti I punti.
Si suppone l’esistenza di una relazione lineare y=A+Bx con A=-1 e B=2.5. Verificare tale ipotesi
mediante il test del chi quadrato
13
11
9
7
5
3
1
-1 0
-3
1
2
3
4
5
6
Test del chi quadrato (cenni)
In corrispondenza dei seguenti valori delle ascisse (tempo): 0s, 2s, 3s, 5s, sono misurati I seguenti
valori della variabile y (spazio =: -1.3 cm, 4.5 cm, 6.3 cm, 11.8 cm).
L’errore sulle x è trascurabile, quello sulle y è pari a 0.4 cm per tutti I punti.
Si suppone l’esistenza di una relazione lineare y=A+Bx con A=-1 e B=2.5. Verificare tale ipotesi
mediante il test del chi quadrato
Calcoliamo il chi quadrato:
y1 A B x1
y A B x
2
2
y3 A B x3
y4 A B x4
1.3 1 2.5 0
0.3 cm
4.5 1 2.5 2
6.3 1 2.5 3
0.5 cm
0.2 cm
11.8 1 2.5 5 0.3 cm
yi A B xi
0.3 0.5 0.2 0.3
2
2.94
2
2
2
2
2
i
i
0.4 0.4 0.4 0.4
2
2
2
2
2
I gradi di libertà sono 4 (ho quattro misure e nessun parametro
ricavato dai dati, A e B infatti sono noti (ipotizzati): Il chi quadrato
ridotto è quindi pari a:
2
2
2.94
0.73
ng
4
Test del chi quadrato (cenni)
In corrispondenza dei seguenti valori delle ascisse (tempo): 0s, 2s, 3s, 5s, sono misurati I seguenti
valori della variabile y (spazio =: -1.3 cm, 4.5 cm, 6.3 cm, 11.8 cm).
L’errore sulle x è trascurabile, quello sulle y è pari a 0.4 cm per tutti I punti.
Si suppone l’esistenza di una relazione lineare y=A+Bx con A=-1 e B=2.5. Verificare tale ipotesi
mediante il test del chi quadrato
Dalla tabella si ricava che la probabilità di avere un valore di chi quadrato ridotto
con 4 gradi di libertà pari a 0.73 è circa 59% (interpolando i valori tabulati per
0.6 e 0.8). L’ipotesi di linearità con i parametri dati può quindi dirsi ben verificata.
Test del chi quadrato (cenni)
Abbiamo introdotto il test del chi quadrato nel caso specifico di una relazione
lineare. E’ tuttavia possibile generalizzare il discorso e usare il test per
valutare quanto i dati misurati si adattano bene ad una funzione teorica
ipotizzata f(x) qualsiasi (retta, parabola, esponenziale, ecc…)
25
20
15
10
5
0
0
100
200
Post-administration time (min)
300
400
FORMULE ED ELEMENTI DA RICORDARE -1
errore (assoluto): x
errore relativo:
media aritmetica: x
errore%: 100
x
xi
i 1 N
x
x
N
N
dev. standard
della media: S x
N
dev. standard: S x
x
(x x)
i 1
2
i
( N 1)
propagazione degli errori:
(x x)
2
i
i 1
N ( N 1)
Sx
N
f ( x1 , x2 ,....x N )
somma e differenze:
prodotti e rapporti:
f ( x1 , x2 ) K x1 x2
n
m
x1
n
f
x1
f
x2
m
x2
2
2
FORMULE ED ELEMENTI DA RICORDARE -2
f ( x)
Gaussiana:
compatibilità: x1 S1
t
media pesata:
X best
N
xi
2
i
e
x 2
2 2
(significato dei parametri e uso
della tabella delle probabilità)
; x2 S 2
S S
2
1
2
2
P (t ) CL 100 P (t )
errore sulla media pesata:
X
best
1
i 1
2
x1 x2
i 1
N
1
2
i
rappresentazione dei risultati FINALI con il corretto numero di
CIFRE SIGNIFICATIVE
1
N
1
i 1
2
i












