La Temperatura termodinamica

La Temperatura termodinamica
p
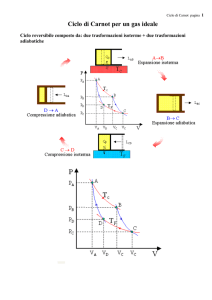
Si considerino i due cicli bitermici reversibili
ABCD e AB’C’D (cicli di Carnot) che lavorano tra
le isoterme T1 e T2 (con T1 > T2): è evidente che il
ciclo AB’C’D, avendo un’area maggiore di quella
del ciclo ABCD produce più lavoro. Nello stesso
tempo esso riceve dall’esterno lungo l’isoterma
AB’ più calore di quanto ne riceva il ciclo più
piccolo.
A
Q1
B
Q1’
B’
LAB’C’D > LABCD
D
Q2
T1
Q2’ C C’
T2
;
Q1’ > Q1
I rendimenti dei due cicli sono rispettivamente:
v
ηAB'C'D =
Q1 ' − Q 2 '
Q '
= 1− 2
Q1 '
Q1 '
ηABCD =
Q1 − Q 2
Q1
= 1−
Q2
Q1
Per il Teorema di Carnot, questi due rendimenti devono essere eguali, perché i due cicli lavorano
tra le stesse temperature. Si ha allora
Q2
Q '
= 2
Q1
Q1 '
;
Q2
Q
= 1
Q 2 ' Q1 '
Pertanto : dato un ciclo di Carnot che lavora tra due isoterme assegnate, lo spostamento di una
delle due linee adiabatiche comporta la variazione proporzionale dei calori scambiati ma non fa
cambiare il rendimento del ciclo.
p
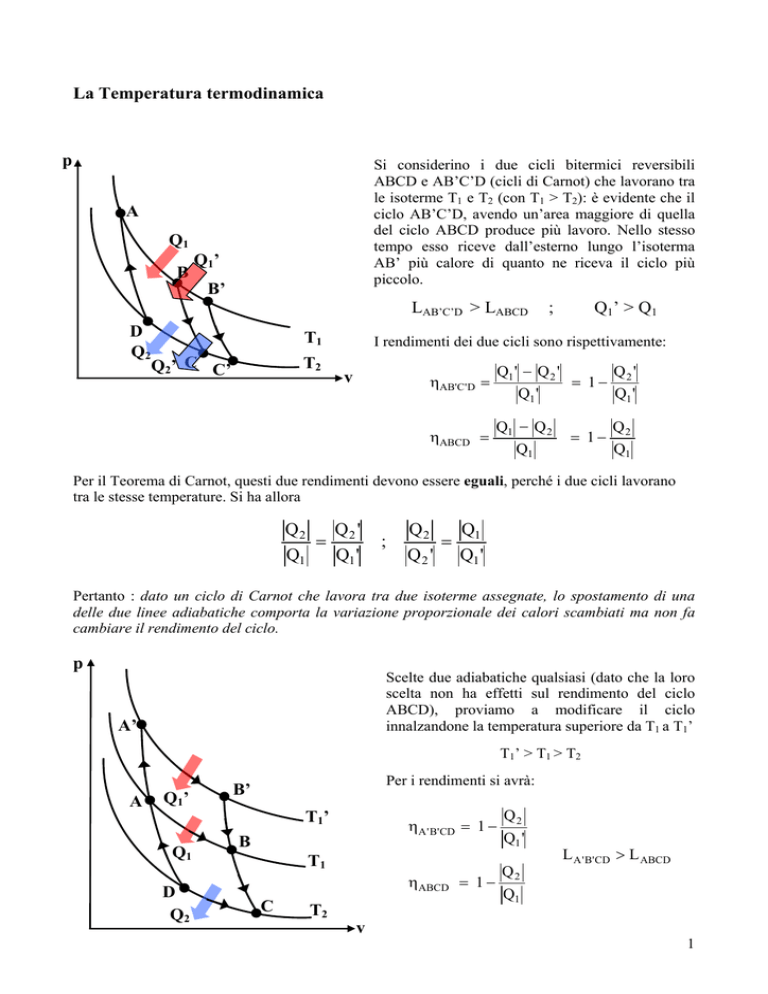
Scelte due adiabatiche qualsiasi (dato che la loro
scelta non ha effetti sul rendimento del ciclo
ABCD), proviamo a modificare il ciclo
innalzandone la temperatura superiore da T1 a T1’
A’
T1’ > T1 > T2
A
Q1’
Per i rendimenti si avrà:
B’
T1’
Q1
D
Q2
ηA ' B' CD = 1 −
B
T1
ηABCD
C
T2
Q2
Q1 '
L A ' B' CD > L ABCD
Q
= 1− 2
Q1
v
1
Essendo LA’B’CD = |Q1’| − |Q2| maggiore di LABCD = |Q1| − |Q2|
si ha
: |Q1’| > |Q1| e quindi:
ηA’B’CD > ηABCD
Pertanto : dato un ciclo di Carnot che lavora tra due adiabatiche assegnate, lo spostamento di una
delle due linee isoterme comporta la variazione del rendimento del ciclo.
In particolare, se si aumenta la temperatura superiore lasciando invariata quella inferiore, il
rendimento del ciclo aumenta.
Questa osservazione indica che il rendimento di una macchina di Carnot, una volta fissata una delle
due temperature (p.es. quella inferiore) ad un valore, peraltro arbitrario, è una funzione (incognita)
della temperatura alla quale il calore viene ricevuto:
ηCarnot = ƒincognita (T1) [fissata T2] = ƒincognita (T1 , T2)
p
Per evitare riferimenti a particolari scale
termometriche, si consideri una scala di
riferimento qualsiasi e si indichino con θ i suoi
valori.
Consideriamo i tre cicli di Carnot rappresentati in
figura che si svolgono tra le stesse adiabatiche e le
tre isoterme θH, θC e θ0 con θH > θC > θ0
QH
1Q
C
3
2
-
θH
-
θC
-
Q0
θ0
v
Il ciclo 1, lavorando tra θH e θC assorbe
QH e cede QC
Il ciclo 2, lavorando tra θC e θ0 assorbe
QC e cede Q0
Il ciclo 3, lavorando tra θH e θ0 assorbe
QH e cede Q0
I tre rendimenti saranno rispettivamente:
Ciclo 1)
η1 = 1 −
Ciclo 2)
η2 = 1 −
Ciclo 3)
η3 = 1 −
QC
QH
Q0
QC
Q0
QH
Considerando la relazione η1 = ϕ (θH , θC) si può scrivere
QH
QC
=
1
= f(θ H , θ C )
1 − ϕ(θ H , θ C )
2
θH
QH
QH
1
QH
Ciclo 1)
QC
QC
θC
3
QC
= f (θ C , θ 0 )
Q0
Ciclo 2)
QC
Q0
2
= f (θ H , θ C )
QH
Ciclo 3)
Q0
Q0
= f (θ H , θ 0 )
θ0
Dalle precedenti relazioni si può ricavare:
QH
QC
⋅
QC
Q0
= f (θ H , θ C ) ⋅ f ( θ C , θ 0 ) =
QH
Q0
= f (θ H , θ 0 ) e quindi : f (θ H , θ C ) =
f (θ H , θ 0 )
f (θ C , θ 0 )
Osservando che θH, θC e θ0 sono tra loro indipendenti e che il rendimento della macchina che opera
tra θH e θC è del tutto indipendente da θ0, la relazione precedente è soddisfatta se la forma della
funzione incognita f(θi , θj) è data dal rapporto di due funzioni semplici ed identiche di θi o θj.
f (θ i , θ j ) =
ψ (θ i )
ψ (θ j )
Si può dimostrare che questa condizione, oltre ad essere sufficiente, è anche necessaria.
E’ importante osservare che nella relazione precedente non appare la temperatura θ0 presa come
riferimento (peraltro arbitrario).
Indicando con T (Temperatura Termodinamica) la funzione ψ(θ), si perviene alla relazione, valida
per la macchina di Carnot che lavora tra le temperature TH e T0:
QH
Q0
=
TH
T0
Questa nuova relazione stabilisce che il rapporto tra due Temperature Termodinamiche è eguale al
rapporto che sussiste tra i calori scambiati dalla Macchina di Carnot che opera tra queste due
Temperature.
3
Fissando una delle due Temperature ad un punto standard T0 (p. es. uno standard fisico) è possibile
fare misure di temperatura “assolute” ed attribuire un preciso valore numerico Ti ad una
temperatura misurando i calori Qi e Q0 scambiati dalla macchina di Carnot che opera tra Ti e T0
Ti = T0 Qi/Q0
Questa scala è indipendente dalla sostanza termometrica, infatti, invece di valutare la dipendenza
dalla temperatura di una particolare caratteristica fisica di una particolare sostanza, si fanno misure
di Energia.
Dalle relazioni trovate precedentemente, che mostrano come la quantità di calore scambiata da una
macchina di Carnot che lavora tra due generiche adiabatiche, vada aumentando con l’aumentare
della temperatura superiore del ciclo, si evince anche che al diminuire della temperatura inferiore
diminuisce il calore ceduto.
Poiché la quantità di calore più piccola che può essere ceduta è zero, esisterà una temperatura
minima (zero assoluto) al di sotto della quale non è consentito andare.
ηC = 1 −
Q2
Q1
= 1−
T2
T1
Al tendere di Q2 → 0 anche T2 → 0.
Lo Zero assoluto non è raggiungibile :
perché T2 = 0 implicherebbe ηC = 1
perché Q2 = 0 implicherebbe che la macchina è monoterma
perché il migliore frigorifero (una macchina di Carnot a funzionamento invertito)
diventa sempre meno efficace al diminuire della temperatura inferiore (ad un dT dallo
Zero assoluto estrarrebbe un δQ)
Lo Zero assoluto è lo stesso per tutte le sostanze :
perché il rendimento della macchina di Carnot è indipendente dalla sostanza lavorante
Lo Zero assoluto ha lo stesso valore di quello dei gas perfetti :
perché il gas perfetto è una delle sostanze che possono essere usate nella macchina di
Carnot
Le temperature della scala termodinamica assoluta sono tutte di un solo segno (o tutte positive
o tutte negative):
perché l’esistenza di un solo valore di segno opposto agli altri comporterebbe la
possibilità di costruire una macchina di Carnot con un rendimento maggiore di uno!
Assegnazione dei valori numerici alla scala assoluta
Thomson (Lord Kelvin) suggerì di usare come punto fisso della scala (a cui attribuire ad arbitrio
un valore numerico) il punto triplo dell’acqua a cui si attribuisce il valore numerico 273,16 K e di
prendere come ampiezza del grado quella della scala centigrada.
Assegnando invece il valore 491,69 al punto triplo dell’acqua si ottiene la scala assoluta Rankine
che ha come ampiezza del grado quella della scala Fahreneit
4
Punto Triplo dell’acqua
T
= 273.16
K
p
= 611,73
Pa
vsolido = 0.0010905125 m3/kg
vliquido = 0.0010002110 m3/kg
vvapore = 206.015657 m3/kg
Si immagini di porre in cascata n macchine di Carnot, in
modo che ogni macchina riceva il calore scaricato dalla
macchina precedente. Ovviamente i serbatoi, cedendo le
stesse quantità di calore che acquistano, non hanno alcun
ruolo tranne quello di fissare i valori delle diverse
temperature alle quali operano le macchine.
T0
Q0
L1
Quali valori devono avere le
temperature affinché le macchine
producano tutte la stessa quantità di
lavoro ?
William Thomson (Lord Kelvin)
1824-1907
Q1
⎛ T ⎞ Q
⎛
Q ⎞
L1 = Q 0 − Q1 = Q 0 ⎜⎜1 − 1 ⎟⎟ = Q 0 ⎜⎜1 − 1 ⎟⎟ = 0 (T0 − T1 )
⎝ T0 ⎠ T0
⎝ Q0 ⎠
T1
Q1
⎛
⎛ T ⎞ Q
Q ⎞
L 2 = Q1 − Q 2 = Q1 ⎜⎜1 − 2 ⎟⎟ = Q1 ⎜⎜1 − 2 ⎟⎟ = 1 (T1 − T2 )
Q1 ⎠
T1 ⎠ T1
⎝
⎝
L2
Q2
Avendo posto, per ipotesi, L1 = L2 = L3 = ...
T2
si ha :
Q2
L3
Q3
Q0
(T0 − T1 ) = Q1 (T1 − T2 ) = Q 2 (T2 − T3 ) = L
T0
T1
T2
ed essendo:
Q 0 Q1
=
nella prima macchina ,
T0
T1
T3
Q3
L4
Q4
Q1 Q 2
=
nella sec onda , e cos ì via L
T1
T2
sarà anche : (T0 − T1 ) = (T1 − T2 ) = (T2 − T3 ) = L
A pari intervalli di temperatura sulla scala assoluta, corrispondono eguali
lavori fatti da macchine di Carnot che lavorano tra gli estremi dell’intervallo
assorbendo il calore scaricato dalla macchina precedente.
5
Notiamo ancora che essendo:
Q0
(T0 − T1 ) = Q 0 ∆T
T0
T0
Q
Q
L 2 = 1 (T1 − T2 ) = 1 ∆T
T1
T1
L1 =
.............................................
Posto ∆T = 1 K (p.es.) i lavori L1, L2, ……. sono eguali e, facendo variare la temperatura in modo
lineare, anche i calori varieranno linearmente.
La scala della temperatura Termodinamica assoluta è lineare nei confronti dei calori
scambiati dalle Macchine di Carnot.
6
EGUAGLIANZA DI CLAUSIUS
Mediante una macchina di Carnot, usata in un ciclo bitermico
reversibile, abbiamo dimostrato che sussiste la proporzionalità tra
i calori scambiati dalla macchina
e le temperature
termodinamiche delle due sorgenti:
Q1
Q2
=
T1
T2
;
Q1
T1
=
Q2
T2
;
Q1
T1
−
Q2
=0 ;
T2
Q1 Q 2
+
=0
T1
T2
In conclusione: in una macchina di Carnot (diretta o inversa) la
somma algebrica dei rapporti tra i calori scambiati alle due
sorgenti con le temperature termodinamiche delle sorgenti, è
nulla.
Consideriamo ora il ciclo ABCDEFGA: si tratta certamente di un
ciclo politermico, in quanto la macchina che lo compie viene
successivamente a contatto con quattro termostati.
Rudolph Gottlieb (Clausius)
1822 - 1888
p
p
A Q11
A
T1
T1
Q1
Q12
G
T4
Q4
G
T4
B
F
T3
Q3
C
T2
Q4
B
Q2
D
F Q
31
T3
E
Q2
C
D
T2
Q32
E
v
v
Il ciclo è composto da quattro isoterme e quattro adiabatiche. E’ facile vedere come il ciclo possa
essere scomposto in tre cicli di Carnot, per ciascuno dei quali vale la relazione trovata sopra.
Si avrà allora per le tre macchine:
Q11 Q 4 Q12 Q 31 Q 2 Q 32
Q
+
=
+
=
+
= 0 e quindi : ∑ i = 0
T1
T4
T1
T3
T2
T3
Ti
7
Se la macchina (lavorando in maniera internamente reversibile) venisse in contatto con infiniti
termostati, le cui temperature differiscono tra loro di una quantità infinitesima, scambiando con
ciascun serbatoio una quantità infinitesima di calore (in maniera esternamente reversibile ossia
essendo il sistema alla stessa temperatura del serbatoio con cui scambia calore), si avrebbe il ciclo
(motore) disegnato in figura.
p
p
v
v
adiabatica
isoterma
E’ possibile immaginare di ridurre il ciclo politermico ad una somma di infiniti termini, ciascuno
dei quali è una macchina di Carnot di area infinitesima.
Le macchine sono ottenute tracciando sul ciclo una serie (infinita) di linee adiabatiche che
individuano i cicli infinitesimi composti dalle adiabatiche stesse e chiuse dai due tratti infinitesimi
della trasformazione originale seguita dal fluido nel percorrere il ciclo.
Essendo infinitesima la trasformazione lungo la quale si scambia il generico elemento di calore δQ,
essa può essere considerata come un tratto di isoterma.
Tuttavia, qualora si volesse verificare di poter scomporre sempre un ciclo politermico in una somma
(anche finita) di cicli di Carnot, senza commettere alcun errore o approssimazione, si potrebbe
considerare la possibilità di chiudere ciascun ciclo elementare sostituendo il tratto di trasformazione
originale con due tratti di linee isoterme
Resta da dimostrare che questa sostituzione non modifica in nulla l’elemento di ciclo originale.
Per far ciò occorre dimostrare che è possibile individuare sempre un ciclo di Carnot che possa
scambiare gli stessi calori impegnati dal generico elemento del ciclo politermico e produrre la stessa
quantità di lavoro.
La somma di questi cicli di Carnot fornirà allora lo stesso lavoro fornito dal ciclo politermico e
scambierà con le sorgenti le stesse quantità di calore.
8
δQ1
T1
p
T2
δQ2
C
A
−
v
adiabatica
isoterma
O
+
D
B
Si consideri il ciclo intrecciato ABOCDOA:
La trasformazione BC rappresenta il tratto di trasformazione del ciclo politermico
Le linee AB e CD sono due tratti di adiabatica
La trasformazione AD è il tratto di isoterma con la quale vogliamo sostituire la
trasformazione BC
Si scelga opportunamente la posizione della isoterma, in modo da creare due aree AOB e COD
eguali.
Percorrendo il ciclo dovrà essere ∑ Q e = ∑ L e e poiché il lavoro, rappresentato dall’area totale del
ciclo, è nullo perché le due aree sono eguali ma percorse in senso opposto, dovrà essere ∑ Q e = 0
Poiché il calore è scambiato solo lungo i tratti BC e AD dovrà essere anche |QAD| = |QBC|
Per ogni macchina di Carnot infinitesima si avrà:
δQ1 δQ 2
+
=0
T1
T2
E per il ciclo politermico reversibile si avrà:
∫rev
δQ
=0
T
Equazione di Clausius per i cicli reversibili
9
δQ
∫
p
ACB
B
C
∫
AB
A
T
δQ
T
δQ
+ ∫
BDA
= ∫
AB
T
δQ
T
=0
non dipende dal percorso
D
v
L’equazione di Clausius mostra pertanto che la quantità (δQ/T)rev gode delle proprietà di una
funzione di stato, è essa stessa una funzione di stato ed è quindi idonea a misurare le variazioni di
Entropia così come si era assunto nella definizione assiomatica del Secondo Principio.
⎛ δQ ⎞
⎟ = S B − SA
∫⎜
T
⎝
⎠ rev
A
B
Nell’espressione (δQ/T)rev la temperatura T è la Temperatura Termodinamica assoluta, infatti
l’espressione stessa è stata ottenuta attraverso la relazione di proporzionalità che esiste tra i calori
scambiati da una macchina di Carnot e le temperature Termodinamiche delle sorgenti.
10
SUPERIORITA’ ASSOLUTA DEL CICLO DI CARNOT
(Rispetto a tutte le macchine politermiche reversibili)
Si è già dimostrato che tutte le macchine bitermiche reversibili che lavorano tra le stesse (due)
temperature devono avere lo stesso rendimento, sia che seguano cicli diversi da quello di Carnot
(cicli a rigenerazione completa) sia che seguano lo stesso ciclo (in questo caso esse potrebbero
differire per la sostanza lavorante).
p
Si consideri un ciclo politermico reversibile in cui
un sistema (per comodità di rappresentazione
supposto p,v,t) compie una serie di trasformazioni
in maniera (internamente) reversibile scambiando
quantità infinitesime di calore in maniera
(esternamente) reversibile con infiniti termostati
aventi temperature differenti di una quantità
infinitesima l’una dall’altra.
T1
Le condizioni di reversibilità impongono che il
sistema lavorante sia sempre in equilibrio con se
stesso e si porti anche in equilibrio termico con le
sorgenti con le quali va a scambiare calore.
T2
v
E’ sempre possibile individuare la temperatura più alta e la temperatura più bassa alle quali si porta
il sistema lavorante durante lo svolgimento del ciclo.
Nella figura le temperature T1 e T2 sono le isoterme tangenti al ciclo politermico nei punti di
massima e minima temperatura.
Supponendo – ed anche questo è sempre teoricamente possibile – di poter distinguere i tratti
infinitesimi di trasformazione in cui il sistema lavorante assorbe o cede calore agli infiniti serbatoi
esterni, si potrà spezzare l’integrale di Clausius in due integrali, l’uno esteso agli infiniti contributi
di calore ricevuti dal sistema (calore positivo entrante) e l’altro ai calori ceduti (calore negativo
uscente).
δQ r
δQ c
δQ
=0= ∫
− ∫
rev T
ricevuto Tr
ceduto Tc
∫
Sostituendo nella relazione di sopra, alle generiche (infinite) temperature Tri e Tci i singoli valori
T1 ≥ Tri e T2 ≤ Tci
si ha :
δQ r
δQ r
>∫
T1
ricevuto Tr
∫
;
∫
ceduto
δQ c
δQ c
<∫
Tc
T2
1
1
∫ δQr − ∫ δQc < 0
T1 r
T2 c
11
Si avrà allora:
Qr
T1
−
Qc
T2
<0 ;
Qr
T1
<
Qc
T2
;
T2 Q c
<
T1 Q r
; 1−
Q
T2
> 1− c
T1
Qr
; ηC > η MRP
Che dimostra che il rendimento della macchina di Carnot che lavora alle due temperature T1 e
T2 è superiore a quello della macchina politermica che lavora tra le temperature estreme T1 e
T2
12
HEAT ENGINE
Ein Bokek Solar Thermal Power Plant
(Israel)
Dead Sea Solar Thermal Power Plant
(Israel)
CANDU PHW Nuclear Reactor
(Canada)
Dungeness “A” Nuclear Reactor
(U.K.)
Larderello Geothermal Steam Plant
(Italy)
West Turrock Conventional coal-fired Steam Plant (U.K.)
Central Steam Power Station
(U.K.)
Calder Hall Nuclear Reactor
(U.K.)
Steam Power Plant
(U.S.A.)
Combined Cycle (Steam & Mercury) Plant
(U.S.A.)
Closed Cycle Gas Turbine
(Switzerland)
Closed Cycle Gas Turbine
(France)
T2 (low)
[K]
303
300
298
298
353
298
298
298
298
298
298
298
T1 (high)
[K]
350
358
573
663
523
840
698
583
923
783
963
953
ηimp ηCarnot
[%]
6
8
27
33
16
36
28
19
40
34
32
34
[%]
13.43
16.20
47.99
55.05
32.50
64.52
57.31
48.89
67.71
61.94
69.06
68.73
Scarto%
[%]
55.3
50.6
43.7
40.1
50.8
44.2
51.1
61.1
40.8
45.1
53.7
50.5
La tabella riporta i valori del rendimento globale (ηimp) di alcuni impianti per la produzione di
potenza.
I valori del rendimento sono stati calcolati mediante il rapporto tra l’energia termica fornita
all’impianto dall’esterno in un certo periodo di tempo (calore solare, quantità di combustibile,
peso di Uranio fissionato, etc.) e l’energia meccanica fornita, nello stesso tempo, dall’impianto
all’esterno, generalmente attraverso una turbina.
Dall’analisi del ciclo termodinamico dei diversi impianti è stato quindi ricavato il valore minimo e
quello massimo delle temperature delle varie sorgenti con le quali il fluido di lavoro scambia calore
durante il ciclo. Con questi due valori è stato calcolato il rendimento teorico (ηCarnot) dell’ipotetico
ciclo di Carnot corrispondente.
Si può osservare che i rendimenti effettivi degli impianti presi in esame risultano molto più bassi dei
corrispondenti valori offerti dalla macchina di Carnot.
Nell’ultima colonna sono riportati infatti i valori degli scarti relativi percentuali, così definiti :
Scarto % =
η Carnot − η Im p
η Carnot
⋅ 100
si nota che la differenza tra il rendimento effettivo dell’impianto e quello (massimo possibile)
offerto dalla macchina di Carnot che lavora tra le temperature estreme del ciclo, è pari mediamente
al 50%.
E’ lecito allora chiedersi a cosa sia imputabile questa differenza tra i rendimenti degli impianti reali
ed il rendimento massimo teorico raggiungibile nelle stesse condizioni dalla macchina di Carnot.
Poiché è evidente che una differenza così notevole non può essere dovuta soltanto a problemi
di natura tecnologica (attriti meccanici, dispersioni termiche, etc.) dobbiamo concludere che il
rendimento di Carnot non è il giusto parametro a cui fare riferimento per giudicare
l’efficienza di una macchina termica per la produzione di potenza.
13
Consideriamo allora:
-
Una macchina bitermica reversibile che opera secondo un ciclo di Carnot
-
Una macchina internamente reversibile che opera secondo un ciclo di Carnot
Ambedue le macchine seguono un ciclo formato da due isoterme e due adiabatiche e scambiano
calore soltanto con l’esterno, rappresentato dalle due sorgenti T1 e T2, ma con la seguente
differenza:
quando la prima scambia calore con l’esterno, essa, oltre ad
essere in equilibrio termico interno, è anche in equilibrio termico
esterno con la sorgente utilizzata. Il ciclo è pertanto internamente ed
esternamente reversibile, infatti si ha:
T1
|Q1|
T1
C
L
T2
|Q2|
∆S tot =
Q1
T1
−
Q2
T2
−
∆S macchina = 0
Q1
T1
+
Q2
T2
=0
∆Sesterno = 0
T2
quando la seconda scambia calore con l’esterno, essa è soltanto
in equilibrio termico interno ma non è in equilibrio termico con la
sorgente utilizzata, ed il suo ciclo internamente reversibile si
svolge tra le temperature T’1 < T1 e T’2 > T2 mentre la macchina,
nel suo complesso, risulta non reversibile per irreversibilità
termiche esterne, infatti si ha:
T1
|Q1|
T’1
C
L
T’2
|Q2|
T2
∆S tot =
Q1
T '1
−
Q2
T'2
∆S macchina = 0
−
Q1
T1
+
Q2
T2
>0
∆Sesterno > 0
Si tratta pertanto di un motore endoreversibile, utilizzato in un ciclo non
reversibile per irreversibilità termiche esterne.
E’ facile rendersi conto che le irreversibilità termiche esterne, quelle dovute ad
una differenza finita di temperatura tra il motore endoreversibile ed i serbatoi,
sono necessarie se vogliamo che la macchina produca un flusso di lavoro, ossia
produca potenza.
14
Abbiamo dimostrato che la Macchina di Carnot è quella che, per date temperature dei due serbatoi
esterni, produce il massimo lavoro possibile per ciclo, realizzando quindi, in maniera continuativa,
la migliore conversione in lavoro del calore prelevato dal serbatoio a temperatura più elevata.
Se vogliamo utilizzare la Macchina di Carnot in un ciclo bitermico reversibile, dobbiamo garantire
che durante le trasformazioni isoterme sussista l’equilibrio termico tra i serbatoi ed il fluido che
evolve nella macchina o almeno che la differenza di temperatura sia infinitesima.
Quest’ultima condizione ci assicura che uno scambio termico tra termostato e fluido può avvenire,
anche se, per trasferire una quantità di calore finita tra i due elementi, è necessario attendere un
tempo infinito o utilizzare scambiatori con superfici infinite.
Una macchina che fornisce una quantità di lavoro finita in un tempo infinito ha
ovviamente potenza nulla.
Se vogliamo realizzare una macchina in grado di produrre una quantità di lavoro finita in un
tempo finito, quindi una macchina in grado di produrre potenza, è necessario mantenere una
differenza finita di temperatura tra la macchina ed i serbatoi.
Questa differenza di temperatura ci assicura che possa scorrere un flusso di calore verso la
macchina che a sua volta produrrà un flusso di lavoro e quindi la potenza richiesta.
Per quello che riguarda la macchina, faremo l’ipotesi che essa sia un motore endoreversibile
funzionante secondo un ciclo di Carnot, mentre l’irreversibilità termica esterna alla macchina
sarà dovuta ad una resistenza termica localizzata tra la macchina ed i serbatoi.
Semplificando al massimo, cioè riducendo il motore endoreversibile ad un cilindro munito di
pistone, si ha la situazione descritta in figura, dove:
Tx è la temperatura (p.es.) della sorgente a temperatura più alta che cede calore al fluido di lavoro
TxC è la temperatura del fluido di lavoro, in equilibrio
TxC
Rx
d
Tx
termico con se stesso ma non in equilibrio con la sorgente. In
questo caso (p. es, per flusso entrante nel motore) Tx > TxC
Rx è la resistenza termica globale (considerata esterna alla
macchina) attraverso la quale il serbatoio e la macchina sono
posti in contatto termico. Supporremo, per ipotesi, che il
valore di Rx non sia dipendente dalla temperatura.
d
è il flusso di calore che si trasmette attraverso la
resistenza termica Rx .
Come sarà chiarito meglio in seguito, il Flusso Termico d
che si trasmette attraverso un elemento di superficie S, di conducibilità K, sulle cui facce è
mantenuta una differenza di temperatura ∆T, può scriversi:
(Fourier)
d = K S ∆T = Cx ∆T = ∆T/ Rx
essendo Cx ,conduttanza globale, l’inverso della resistenza termica globale Rx .
15
Nello schema di figura è possibile individuare le parti che
compongono la macchina:
- il motore endoreversibile C che evolve secondo un ciclo
R1
di Carnot tra le temperature T1C e T2C. producendo la
d1
∆T1
potenza W.
T1C
- le resistenze termiche R1 ed R2, esterne al motore.
W
- i due serbatoi (termostati) a temperatura T1 e T2 che
T2C
scambiano rispettivamente i flussi termici d 1 e d 2 con
il motore.
∆T2
d2
Come nella legge di Ohm (∆V = I R), il flusso termico d
R2
(nell’analogia, la corrente I) attraversando la resistenza termica
R (elettrica) produce ai suoi capi una differenza di Temperatura
T2
∆T (di Tensione ∆V).
Secondo quanto stabilito dal primo Principio, usando le Conduttanze termiche C al posto delle
Resistenze R , si ha anche:
T1
C
W = d 1 - d 2 = C1 ∆T1 - C2 ∆T2
Facendo variare opportunamente il Flusso Termico estratto dalla sorgente a temperatura
superiore si possono avere le seguenti situazioni:
quella della macchina bitermica reversibile, in cui il calore, attraversando le resistenze
termiche in un tempo infinito, non produce alcuna differenza di temperatura ai capi delle
resistenze stesse. In questa situazione viene prodotto il massimo lavoro ma nessuna
potenza.
-
-
infinite situazioni intermedie in cui il flusso termico estratto dalla sorgente superiore
produce un flusso finito di lavoro nel motore endoreversibile e quindi una potenza finita.
quella in cui la somma dei due ∆T è pari alla differenza di temperatura T1 - T2; in questo
caso il salto di temperatura a disposizione del motore endoreversibile è nullo ed esso non
produce alcun lavoro. In questa situazione si ha ancora potenza nulla.
p T1 ≡ T1C
A
T1C
Nelle figure sono rappresentati i
casi sopra descritti:
-
A’
T2CA’’≡ D’’
-
D’
T2 ≡ T2C
D
B
B’
B’’≡ C’’
C’
C
v
-
Ciclo ABCD = caso
estremo della macchina
bitermica reversibile
Ciclo
A’B’C’D’(uno
degli
infiniti
cicli
possibili) = macchina con
irreversibilità
termiche
esterne.
Ciclo A”B”C”D” = caso
estremo
del
motore
endoreversibile di area
nulla.
16
R1
d1
∆T1=0
Q1
T1
T1
T1
T1C = T1
R1
∆T1
T1C
T1C= T2C
W=0
d 1=d 2
T2C
T2C = T2
∆T2=0
Q2
W
C
Lmax
C
d2
R2
∆T2
R2
Lavoro finito L= Lmax
Tempo infinito
Potenza W=0
∆T2
T2
T2
T2
∆T1
Lavoro finito L
Tempo finito
Potenza W
Lavoro L = 0
Tempo finito
Potenza W=0
Ora è evidente che il motore endoreversibile produce una potenza finita nei casi intermedi e non
produce potenza nei casi estremi.
Pertanto è possibile ipotizzare l’esistenza di una relazione tra la potenza W ed i due ∆T o, più
precisamente, con uno solo dei due ∆T, poiché essi sono legati tra loro dalle relazioni valide per la
macchina di Carnot.
Riprendiamo quindi in considerazione il principio di conservazione dell’energia (scritto nell’unità
di tempo).
W = d 1 - d 2 = C1 ∆T1 - C2 ∆T2
per la macchina di Carnot vale la relazione:
d 2 / d 1 = T2C / T1C
Da cui, considerando i ∆T intrinsecamente positivi, si ha:
T1
C 2 ∆T2 T2C T2 + ∆T2
=
=
C1∆T1 T1C
T1 − ∆T1
∆T1
T1C
W
C
T2C
∆T2
ricavando ∆T2 in funzione di ∆T1 si ottiene la seguente relazione:
∆T2 =
C1 T2 ∆T1
C 2 T1 − (C1 + C 2 ) ∆T1
T2
17
che consente di esprimere W in funzione di ∆T1 soltanto:
W (∆T1 ) = C1∆T1 ⋅
C 2 (T1 − T2 ) − (C1 + C 2 ) ∆T1
C 2 T1 − (C1 + C 2 ) ∆T1
Questa espressione consente di calcolare la potenza meccanica che si può ottenere da un motore
endoreversibile di date caratteristiche termofisiche costruttive (le caratteristiche C1 e C2),
sfruttando due termostati aventi rispettivamente temperature T1 eT2, al variare della differenza di
temperatura ∆T1 tra la sorgente superiore ed il motore stesso (essendo ∆T2 fissato in conseguenza
delle relazioni valide per la Macchina di Carnot).
La funzione W=f(∆T1) si annulla ovviamente per ∆T1 = 0, cioè quando la macchina, nel suo
complesso, è una macchina bitermica reversibile, ma anche nel caso in cui:
∆T1 =
C2
(T1 − T2 )
C1 + C 2
∆T2 =
C1
(T1 − T2 )
C1 + C 2
ma in questo caso si ha anche:
e quindi:
∆T1 + ∆T2 = T1 − T2
E’ facile vedere che questa condizione corrisponde all’altro caso estremo sopra evidenziato, quello
per cui il motore endoreversibile lavora tra due temperature eguali, senza produrre alcun lavoro per
ciclo.
Indicando con ∆T1LIM il valore limite del ∆T1 per il quale la funzione W=f(∆T1) passa per lo
zero, poiché tra ∆T1 = 0 e ∆T1 = ∆T1LIM la macchina produce una potenza diversa da zero, essa
deve esibire almeno un punto di massimo.
Allo scopo di semplificare i calcoli considereremo C1 = C2, posizione che trae la propria
giustificazione dal fatto di avere precedentemente supposto che il valore della resistenza termica
interposta tra termostati e cilindro di lavoro non dipenda dalla temperatura.
Si ha allora:
C ∆T1 (T1 − T2 ) − 2C ∆T12
W (∆T1 ) =
T1 − 2 ∆T1
W
La funzione, che ha evidentemente la
forma di un’iperbole non equilatera, è
sempre positiva tra ∆T1 = 0 e ∆T1 =
∆T1LIM e possiede un solo punto
massimo che può ottenersi facilmente
eguagliando a zero la sua derivata prima.
∆T1
0
∆T1MAX
∆T1LIM
18
[
]
dW [C (T1 − T2 ) − 4 C ∆T1 ] ⋅ [T1 − 2 ∆T1 ] + C ∆T1 (T1 − T2 ) − 2 C ∆T12 ⋅ 2
=
d∆T1
(T1 − 2 ∆T1 ) 2
posto eguale a zero il numeratore si ha la seguente equazione di secondo grado:
T1
(T1 − T2 ) = 0
4
∆T12 − T1∆T1 +
che ammette due soluzioni:
∆T1MAX =
(
1
T1 ±
2
(
1
T1 +
2
)
1
(T1 − T2 ) è evidente che la soluzione positiva
2
e ricordando che, con le ipotesi fatte, ∆T1LIM =
∆T1MAX =
T1 T2
)
T1 T2 si trova a destra di ∆T1LIM che è il valore limite di utilizzazione
della macchina come motore termico ed è pertanto da scartare.
Resta la soluzione negativa:
(
∆T1MAX =
1
T1 −
2
∆T1MAX =
C2
T1 −
C1 + C 2
ed anche :
T1 T2
)
(
(
con C1 = C 2
T1 T2
∆T2 MAX =
1
− T2 +
2
∆T2 MAX =
C1
− T2 +
C1 + C 2
T1 T2
(
)
)
in generale
con C1 = C 2
T1 T2
)
in generale
Dai valori di ∆T1MAX e di ∆T2MAX si possono ricavare i valori di temperatura con cui lavora la
macchina endoreversibile di Carnot che produce la massima potenza:
T1C = T1 − ∆T1MAX
T2C = T2 + ∆T2 MAX
Si ha quindi:
=
=
T2C
=
T1C
1
T1 ⋅
2
(
1
T2 ⋅
2
T1 + T2
(
)
T1 + T2
)
T2
T1
19
Pertanto il rendimento ηCTF della Macchina di Carnot che lavora “a tempo finito”, producendo la
massima potenza, utilizzando due sorgenti attraverso due opportune resistenze termiche e quindi
con irreversibilità di tipo termico esterno, può esprimersi sia in funzione delle temperature ai capi
del motore endoreversibile sia direttamente in funzione delle temperature delle sorgenti.
ηCTF = 1 −
T2C
T2
= 1−
T1C
T1
(Curzon & Ahlborn)
Si può dimostrare che questo risultato, ottenuto nell’ipotesi C1 = C2 vale anche per
C1 ≠ C2.
Si ha pertanto:
Il rendimento a potenza massima di un motore endoreversibile funzionante con un
ciclo di Carnot è funzione esclusivamente delle temperature dei serbatoi e non
dipende né dalle caratteristiche termofisiche dei materiali impiegati per costruirlo né
dal fluido lavorante.
Così come il rendimento della macchina di Carnot, il rendimento a potenza
massima è una caratteristica termodinamica.
HEAT ENGINE
Ein Bokek Solar Thermal Power Plant
(Israel)
Dead Sea Solar Thermal Power Plant
(Israel)
CANDU PHW Nuclear Reactor
(Canada)
Dungeness “A” Nuclear Reactor
(U.K.)
Larderello Geothermal Steam Plant
(Italy)
West Turrock Conventional coal-fired Steam Plant (U.K.)
Central Steam Power Station
(U.K.)
Calder Hall Nuclear Reactor
(U.K.)
Steam Power Plant
(U.S.A.)
Combined Cycle (Steam & Mercury) Plant
(U.S.A.)
Closed Cycle Gas Turbine
(Switzerland)
Closed Cycle Gas Turbine
(France)
T2 (low)
[K]
303
300
298
298
353
298
298
298
298
298
298
298
T1 (high)
[K]
350
358
573
663
523
840
698
583
923
783
963
953
ηimp
ηCTF
[%]
6
8
27
33
16
36
28
19
40
34
32
34
[%]
6.96
8.46
27.88
32.96
17.84
40.44
34.66
28.51
43.18
38.31
44.37
44.08
Scarto%
[%]
13.7
5.4
3.2
-0.1
10.3
11.0
19.2
33.3
7.4
11.2
27.9
22.9
La tabella riporta nuovamente i valori del rendimento globale (ηimp) degli impianti per la
produzione di potenza presi in considerazione all’inizio del capitolo, rivisti alla luce del rendimento
a massima potenza.
Si può osservare che i rendimenti effettivi degli impianti presi in esame risultano ora paragonabili
con i corrispondenti valori (ηCTF) offerti dalla macchina di Carnot funzionante “a tempo finito”
grazie alle irreversibilità termiche esterne opportunamente aggiunte.
Nell’ultima colonna sono riportati infatti i valori degli scarti relativi percentuali, così definiti :
Scarto % =
ηCTF − ηIm p
ηCTF
⋅100
si nota che la differenza tra il rendimento effettivo dell’impianto e quello a massima potenza offerto
dal motore endoreversibile è pari mediamente al 14%.
20
Supponiamo che la sorgente superiore abbia la temperatura T1 = 1000 K (la più alta tra quelle
indicate nella tabella) e quella inferiore sia alla temperatura T2 = 300 K (praticamente quella
dell’ambiente) e che i valori delle conducibilità C1 e C2 siano entrambi pari a 1 W/K, valore scelto
soltanto per semplificare i calcoli.
Il grafico mostra l’andamento della funzione W= f (∆T1) calcolata con i dati sopra indicati.
E’ facile osservare che la funzione si annulla per ∆T1=0 e per ∆T1=∆T1(LIM) ed esibisce un
massimo per ∆T1=∆T1(MAX) , questi valori possono calcolarsi attraverso le relazioni:
∆T1( LIM) =
C2
(T1 − T2 ) = 1 (1000 − 300) = 350 K
C1 + C 2
2
∆T1( MAX) =
(
)
C2
1
T1 − T1T2 = (1000 − 547.72) = 226.14 K
C1 + C 2
2
mentre la potenza massima fornita dalla macchina è:
WMAX= f [ ∆T1(MAX)] = 102.27 Watt
21
Nel punto di massimo la temperatura più alta del motore endoreversibile è :
T1C = T1- ∆T1(MAX) = 1000 – 226.14 = 773.9 K
Mediante la relazione di Fourier è possibile calcolare il flusso termico entrante :
d 1 = C1 (T1-T1C) = 1·(1000-773.9) = 226.14 Watt
Da questi dati può ricavarsi il rendimento del motore endoreversibile funzionante a massima
potenza :
ηCTF = Wmax /d 1 = 102.27 / 226.14 = 0.452
Che è (ovviamente) lo stesso valore che si poteva ottenere immediatamente dalla relazione di
Curzon & Ahlborn:
η CTF = 1 −
T2
300
= 1−
= 1 − 0.548 = 0.452
T1
1000
Se il motore endoreversibile lavorasse come una macchina di Carnot inserita in un ciclo
bitermico reversibile, il suo rendimento sarebbe :
ηC = 1 −
T2
300
= 1−
= 0.7
T1
1000
22
DISEGUAGLIANZA DI POTIER & PELLAT
Consideriamo un ciclo politermico non reversibile per irreversibilità di tipo termico esterno.
Si tratta di un ciclo motore internamente reversibile (il sistema segue trasformazioni isoterme ed
adiabatiche restando sempre in condizioni di equilibrio interno) in cui gli scambi di calore tra il
sistema lavorante ed i serbatoi (termostati) esterni avvengono sotto una differenza finita di
temperatura.
Nella figura, che rappresenta un possibile ciclo non reversibile per irreversibilità di tipo termico
esterno, le temperature T’i rappresentano le temperature (assolute) dei quattro serbatoi esterni che
scambiano calore con il sistema, mentre le Ti rappresentano le temperature (assolute) alle quali si
trova il sistema mentre scambia calore con il serbatoio T’i.
I calori Qei sono i calori scambiati tra i quattro serbatoi ed il sistema lavorante. Si consideri il segno
(implicito) dei calori Qei riferito al sistema lavorante.
p
Sarà pertanto:
Qe1
T’4
Qe4
T4 T1
T’1
Qe2
T2
Qe3
T3
-
Qe1 > 0 essendo T’1 > T1
-
Qe2 > 0 essendo T’2 > T2
-
Qe3 < 0 essendo T’3 < T3
-
Qe4 < 0 essendo T’4 < T4
il sistema produce il lavoro L (positivo)
dato dall’area del ciclo.
T’2
-
L>0
T’3
v
Un sistema lavorante con n serbatoi potrà essere così schematizzato:
T’2
T’1
Qe1
Qe2
T’3
Qe3
T’n
Qen
I segni dei calori
scambiati sono impliciti
e riferiti al sistema
lavorante :
Qei > 0 se entrante nel
sistema
Qei < 0 se uscente dal
sistema
Sistema lavorante
L
(Ovviamente i calori
non potranno essere
tutti entranti o tutti
uscenti)
23
Il nostro obiettivo è quello di trovare una relazione tra le temperature T’i dell’ambiente esterno che
interagisce con il sistema lavorante e l’energia termica Qe fornita al sistema dall’esterno.
Si osservi che le temperature T’i potrebbero essere le uniche temperature accessibili (misurabili) in
quanto messe a disposizione da sorgenti esterne (una caldaia, un reattore nucleare), mentre le
temperature alle quali si svolge il ciclo (internamente reversibile) del sistema potrebbero non essere
accessibili.
Per ottenere la relazione cercata ricorriamo ad un artifizio : supponiamo di collegare tutti i serbatoi
T’i ad un unico termostato a temperatura T0 attraverso altrettante macchine di Carnot mediante le
quali – per ogni ciclo compiuto dal sistema - ciascun serbatoio riceverà la quantità di calore che ha
ceduto al sistema o perderà la quantità di calore che ha ricevuto dal sistema, tornando perciò nelle
condizioni iniziali.
T0
q1
Lc1
C1
q2
Lc2
-Qe1
C2
-Qe2
T’2
T’1
Qe1
Qe2
q3
Lc3
C3
-Qe3
qn
Lcn
-Qen
T’3
Qe3
Sistema lavorante
Cn
T’n
Qen
Ls
Per ottemperare a questa condizione le macchine di Carnot dovranno ricevere una certa quantità di
lavoro dall’esterno o produrre lavoro all’esterno, in relazione al loro tipo di funzionamento.
Nell’esempio che segue si è fatta l’ipotesi che il serbatoio T’i abbia ceduto il calore Qei al sistema
lavorante e quindi sia stato reintegrato con il calore qui (pari a |Qei|) dalla macchina di Carnot Ci.
La macchina Ci potrà fornire il calore qui al serbatoio T’i, lavorando da macchina, nel caso che la
temperatura T0 si trovi ad essere maggiore di T’i (come avviene nell’esempio), assorbendo il calore
24
qei dal termostato T0 e producendo verso l’esterno il lavoro LCi oppure, nel caso che la temperatura
T0 si trovi ad essere minore di T’i lavorare da pompa di calore, assorbendo dall’esterno il lavoro LCi
e scaricando il calore qei nel termostato T0
Nel caso considerato come esempio può scriversi, riferendosi
alla relazione valida in generale per la macchina di Carnot:
T0
q ei q ui
+
=0
T0 T 'i
qei
Lci
Ci
ma anche :
q ei (− Q ei )
+
=0
T0
T 'i
La seconda espressione evidenzia il fatto che il calore qui è
sempre eguale a |Qei| ma, per il serbatoio T’i (e quindi anche per
il sistema lavorante) è di segno opposto.
qui [ -Qe1 ]
Questa relazione può essere scritta per tutte la macchine di
Carnot ed è sempre valida, a prescindere dal vero segno che
hanno i calori scambiati rispetto al sistema lavorante.
T’i
Potremo scrivere allora:
Qei
q1 ⎛ − Q e1 ⎞
⎟=0
+⎜
T0 ⎜⎝ T '1 ⎟⎠
q 2 ⎛ − Qe2 ⎞
⎟=0
per la macchina C 2 :
+⎜
T0 ⎜⎝ T '2 ⎟⎠
per la macchina C1 :
Sistema lavorante
Ls
per la macchina C3 :
q 3 ⎛ − Q e3 ⎞
⎟=0
+⎜
T0 ⎜⎝ T '3 ⎟⎠
...............................
...............................
per la macchina C n :
q n ⎛ − Q en
+⎜
T0 ⎜⎝ T 'n
⎞
⎟⎟ = 0
⎠
e sommando :
Q
1
∑i q i = ∑i ei
T0
T 'i
Facendo compiere un ciclo completo al sistema lavorante ed alle macchine di Carnot, dovrà aversi,
in accordo con il Primo Principio della termodinamica,:
∑i q i = ∑i L tot = LS + ∑i LCi ≤ 0
Infatti :
-
Il lavoro Ltot è dato dalla somma del lavoro prodotto dal sistema lavorante (Ls > 0 per
ipotesi) più i lavori prodotti/assorbiti dalle macchine di Carnot.
25
-
Gli unici calori che possono essere utilizzati per produrre lavoro sono quelli (qi)
scambiati dal termostato T0, infatti tutti i serbatoi T’i hanno compiuto un ciclo ritornando
nelle loro condizioni iniziali.
L’unica sorgente attiva è allora il termostato T0 e quindi tutto il complesso sistema
lavorante + macchine di Carnot è una macchina monoterma.
Il secondo Principio della termodinamica stabilisce che una macchina monoterma non
può fornire lavoro (positivo), pertanto Ltot deve essere nullo o negativo.
Si ha quindi:
∑ i q i = T0 ∑ i
Q ei
=L≤0
T 'i
ed essendo T0 > 0
si ha :
∑i
Q ei
≤0
T 'i
L’ultima disequazione, detta “Diseguaglianza di Potier e Pellat” esprime la relazione esistente in
una macchina politermica non reversibile per irreversibilità di tipo termico esterno, tra i calori
scambiati dalla macchina (col segno riferito alla macchina) e le temperature delle sue sorgenti
esterne.
Supponendo che gli scambi siano invece reversibili, e quindi che la temperatura del sistema sia
eguale a quella del serbatoio col quale il sistema si trova a scambiare calore (T’i = Ti), si potrebbe
invertire il funzionamento della macchina facendola funzionare da pompa di calore, invertendo
anche il funzionamento delle macchine di Carnot.
Tutti i calori cambierebbero segno, invertendo così anche il senso della disuguaglianza finale;
dovrebbe aversi allora contemporaneamente:
∑i
Q ei
≤0
Ti
e
∑i
Q ei
≥0
Ti
da cui : ∑ i
Q ei
= 0 ( rev )
Ti
Estendendo ad infinito il numero dei serbatoi, si hanno le due relazioni fondamentali:
δQ
<0
irrev T '
Potier & Pellat
∫
δQ
=0
rev T
Clausius
∫
E’ opportuno osservare che la diseguaglianza di Potier e Pellat non ha nulla a che fare con
l’Entropia, essa infatti esprime il rapporto tra i calori scambiati dal sistema (con il segno riferito al
sistema) e le temperature dei serbatoi esterni.
Qualora si volesse calcolare la variazione di Entropia dell’ Universo in seguito all’esecuzione di
un ciclo non reversibile per irreversibilità di tipo termico esterno, si dovrebbero valutare
separatamente la variazione di Entropia del sistema e quella dell’esterno, rappresentato dai
serbatoi che lavorano col sistema.
E’ facile vedere che la variazione di Entropia del sistema è nulla (perché il sistema compie un
ciclo) mentre quella dei serbatoi è espressa sempre dalla diseguaglianza di Potier e Pellat nella
quale però è necessario invertire i segni dei calori per riferirli ai serbatoi.
essendo ∆Sest = ∫
− δQ
> 0 si ha : ∆S tot = ∆Sest + ∆Ssist > 0
T'
26
Riepilogo delle relazioni esistenti tra le temperature della generica macchina e
quelle delle sorgenti esterne
p
p
A
Q1
T1MAX
B
D
Q2
+
T1=T1
C
T2=T2C
T2MIN
v
Macchina Bitermica reversibile
Macchina Politermica reversibile
Q1 Q 2
+
=0
T1 T2
p
v
∫
δQ
=0
T
p
T1
A
T’i
δQ1
Ti
A’
T’i > Ti
Q1
D’
T2
D
T1
Q2
B
T2
Ti
B’
T’i δQ
2
C’
C
Macchina di Carnot in un ciclo bitermico
non reversibile per irreversibilità termiche
esterne
Q1 Q 2
+
<0
T1 T2
T’i < Ti
v
v
Macchina Politermica in un ciclo non
reversibile per irreversibilità termiche
esterne
∫
δQ
<0
T 'i
27
DIAGRAMMI ENTROPICI
Il diagramma di Clapeyron ci ha consentito di rappresentare sul piano Pressione, Volume (o volume
specifico se ci riferiamo ad 1 kg di sostanza) il lavoro scambiato da un sistema P,V,T durante una
trasformazione aperta quasi-statica mediante l’area sottesa dalla trasformazione stessa o il lavoro
fornito da un sistema motore mediante l’area racchiusa dal ciclo eseguito - sempre in maniera quasistatica - dalla macchina.
Riportando su un diagramma l’Entropia (entropia specifica se ci riferiamo ad 1 kg di sostanza) in
ascissa e la Temperatura (termodinamica) in ordinata, otteniamo il diagramma Entropico o
diagramma T,S.
Nel diagramma Temperatura-Entropia è possibile valutare il calore scambiato da un sistema P,V,T
durante una trasformazione aperta reversibile mediante l’area sottesa dalla trasformazione stessa o il
lavoro fornito da un sistema motore, mediante l’area racchiusa da un ciclo eseguito - sempre in
maniera reversibile - dalla macchina.
Il fatto che in ambedue i diagrammi l’area di un ciclo rappresenti sempre il lavoro fornito dalla
macchina è conseguenza evidente del I° Principio:
Qe = ∆U + Le
Si noti che sul diagramma P,V l’area del ciclo misura il lavoro in unità meccaniche mentre sul
diagramma T,S il lavoro è rappresentato in unità termiche, le aree sono quindi proporzionali.
Usando le stesse unità per l’Energia, le due aree saranno eguali.
⎛ δQ ⎞
dS = ⎜
⎟
⎝ T ⎠ rev
;
(δQ )rev = TdS
T
B
; Q AB = ∫ TdS
B
A
Sul piano T,S le linee isocore hanno inclinazione maggiore
rispetto alle isobare; infatti, essendo :
T
⎛ ∂S ⎞
⎛ δQ ⎞
cp = ⎜
⎟
⎟ = T⎜
⎝ ∂T ⎠ p
⎝ dT ⎠ p
⎛ δQ ⎞
⎛ ∂S ⎞
cv = ⎜
⎟ = T⎜
⎟
⎝ dT ⎠ v
⎝ ∂T ⎠ v
poichè c p è sempre > c v si ha :
A
dS
T
S = cost
⎛ ∂S ⎞
⎛ ∂S ⎞
⎟
⎟ >⎜
⎜
⎝ ∂T ⎠ p ⎝ ∂T ⎠ v
S
v = cost
p = cost
T = cost
⎛ ∂T ⎞ ⎛ ∂T ⎞
⎜
⎟ <⎜
⎟
⎝ ∂S ⎠ p ⎝ ∂S ⎠ v
P
S
28
Per un ciclo si ha:
T
L
η=
Q1
B
essendo
C
Q1 = ∫ T dS calore ricevuto
A
ABC
Q 2 = ∫ T dS calore ceduto
D
–
CDA
L = Q1 − Q 2
+
l' area del ciclo
S
E’ facile dedurre dal diagramma quali parti del ciclo corrispondono a trasformazioni nelle quali il
calore viene ceduto dal sistema alle sorgenti esterne e quelle in cui il sistema riceve calore dalle
sorgenti esterne.
Basta osservare infatti che a partire dal punto A e fino al punto C, che corrispondono a tratti
infinitesimi di adiabatica, il dS è positivo (calore ricevuto), mentre nel tratto CDA il dS è negativo
(calore ceduto).
Sul diagramma T,S il ciclo di Carnot assume una forma
particolarmente semplice.
T1
Il rendimento del ciclo può essere valutato direttamente
dal rapporto dei segmenti (T1-T2) e T1
T
+
T2
–
S
29