CHEMIOMETRIA
Federico Marini
La misura chimica: base per prendere decisioni
• Le misure chimiche spesso rappresentano la base su cui
prendere importanti decisioni in diversi ambiti:
–
–
–
–
Analisi cliniche
Controllo e monitoraggio di processi industriali
Protezione dell’ambiente
Controllo di qualità degli alimenti e delle merci in genere
• Chiaramente, per poter fornire la base a tali processi
decisionali, la misura chimica deve essere affidabile.
La misura chimica - 2
• La quantità e qualità delle informazioni sulla base delle quali
si prendono le decisioni dipende da tre fattori critici legati al
processo di misura:
– Proprietà chimiche (stechiometria, cinetica, bilanci di massa, equilibri)
– Proprietà fisiche (p, T, bilanci energetici, transizioni di fase)
– Proprietà statistiche (fonti di errore, controllo di fattori interferenti,
calibrazioni, modelli di risposta)
• Un’informazione affidabile può essere ottenuta solo quando
ciascuno di questi fattori sia compreso e controllato.
• Ruolo della statistica – e soprattutto della chemiometria – è
affrontare i problemi legati al terzo di questi fattori.
La chemiometria
• Termine coniato nel 1971 per descrivere l’uso crescente di
modelli matematici, principi statistici ed altri modelli logici
nell’ambito della chimica, e in particolare della chimica
analitica.
• Ambito interdisciplinare che coinvolge statistica multivariata,
modellazione matematica, computer science e chimica
analitica.
• Tra i principali campi:
– Calibrazione, validazione e prove di significatività
– Ottimizzazione di misure chimiche e di procedure sperimentali
– Estrazione della massima informazione chimica rilevante dai dati
analitici a disposizione
La chemiometria - 2
• Per molti aspetti, figlia della statistica, dei computer e
dell’”era informatica”
• Il suo sviluppo è stato reso necessario dai rapidi avanzamenti
tecnologici soprattutto nell’ambito della strumentazione
analitica negli ultimi 40 anni.
• Queste strumentazioni hanno reso possibile l’estrazione di
più dati simultaneamente da una misura (ad es registrazione
dell’intero spettro vs lettura di A ad una singola l).
• Poter considerare la distribuzione di più variabili
simultaneamente fornisce maggior informazione che
considerare una variabile alla volta (vantaggio multivariato).
• Questa informazione aggiuntiva si presenta nella forma della
correlazione
Ulteriori vantaggi dell’approccio multivariato
• Possibilità di ridurre il rumore sperimentale, quando
molte variabili “ridondanti” sono misurate allo
stesso tempo.
• Possibilità di usare misure non completamente
selettive, lasciando alle tecniche di analisi dei dati
la possibilità di eliminare il contributo degli
interferenti.
• Possibilità di identificare campioni non autentici o
anomali in maniera più efficace (attraverso i residui
del modello).
Richiami di statistica di base
Introduzione
• Immaginiamo di voler confrontare un metodo analitico
innovativo con uno di routine.
• Per far questo, preleviamo diverse aliquote di campioni che
analizziamo con entrambi e utilizziamo i risultati ottenuti per
verificare quale metodo sia il “migliore” [NOTA: migliore può
significare tante cose: limite di rivelabilità, errore, purezza,
rapidità]
• Tuttavia, un confronto effettuato in questa maniera può non
rispondere all’interrogativo che ci si pone:
– Chi ha messo a punto il metodo innovativo è particolarmente esperto
nell’utilizzarlo e lo ha ottimizzato; questo può non dirsi se gli stessi
ricercatori applicano il metodo di routine
• La domanda che ci si dovrebbe porre:
– I dati ottenuti dalla misura dei campioni con i due metodi sono
sufficienti a dirmi quale sia il migliore o rifletteranno solamente il fatto
che i ricercatori sono più bravi a far funzionare il loro metodo?
Importanza delle ipotesi
• Senza un’opportuna progettazione, si può buttar via un
sacco di tempo e denaro e si è più soggetti ad errori.
• Le scienze applicate non dovrebbero mai partire dalla
raccolta dei dati, ma dalla formulazione di ipotesi.
• Una volta formulate una serie di domande, si possono
progettare esperimenti per esser sicuri che i dati raccolti
servano a rispondere a queste domande.
• Con un approccio di questo tipo si può ad esempio verificare
che alcune variabili non abbiano effetto sul risultato e quindi
che non sia più necessaria la loro misura.
• La qualità di ogni modello è strettamente dipendente dalla
qualità dei campioni utilizzati per costruirlo.
• Ottenere campioni rappresentativi senza una progettazione
opportuna degli esperimenti è difficile se non impossibile.
Misure ed errori
• La scienza sperimentale è una disciplina quantitativa che
spesso dipende dall’esecuzione di misure numeriche.
• Una misura numerica non è significativa senza una stima
dell’errore o dell’incertezza associata
• La statistica è un valido strumento per descrivere alcuni tipi di
errori o incertezze nei dati.
• Tuttavia non bisogna mai utilizzare la statistica in maniera
cieca, ma sempre collegarne i risultati ai dati che si sono
misurati e alla nostra conoscenza del problema.
• Es: Se misuro l’altezza media di una classe e trovo 234 cm,
o sto insegnando ad una squadra di basket oppure quella
media è per qualche motivo sbagliata:
– errore nel calcolo della media
– dati iniziali
Misure ed errori - 2
• L’errore numericamente più grande domina.
• Se si usa una bilancia accurata al centesimo di grammo per
pesare un grammo di standard purissimo, l’accuratezza con
cui conosciamo la quantità di standard sarà comunque l’1%.
• La statistica non può essere considerata un metodo per
trovare un senso anche a partire da dati cattivi
• I risultati di qualsiasi test statistico riflettono la qualità dei dati
di partenza: se i dati sono cattivi, anche le conclusioni che se
ne possono trarre saranno povere.
Tipi di errore
• Errore grossolano: causato ad esempio da un problema
strumentale, quale calo di tensione, rottura di una lampada, o
da contaminazione del campione o errata etichettatura. La
loro presenza rende l’esperimento inutile. Se non si
effettuano misure replicate sono difficili da identificare.
• Errore sistematico: derivano da imperfezioni nella procedura
sperimentale che possono risultare in bias, ovvero gli errori
hanno tutti la stessa direzione. Possono risultare da
un’errata calibrazione, dall’uso incorretto della vetreria
volumetrica o dalla presenza di interferenti. Possono essere
identificati e corretti.
• Errore casuale: produce risultati che si distribuiscono attorno
al valore medio. Si usa la statistica per descrivere questo tipo
di errori, che in genere non possono essere controllati.
Idealmente dovrebbe essere il minore possibile.
Un po’ di nomenclatura
• Esattezza: Definisce quanto le misure ottenute siano vicine al
valor vero. Piccolo errore sistematicoè grande esattezza.
• Precisione: Definisce la dispersione dei valori attorno alla
media. Piccolo errore casuale è grande precisione.
• Ripetibilità: Definisce l’accordo tra misure replicate utilizzando
gli stessi: metodo, campione, operatore, strumentazione,
laboratorio, tempo, etc.
• Riproducibilità: Definisce l’accordo tra misure replicate
utilizzando gli stessi metodo e campione, ma variando:
operatore, strumentazione, laboratorio, tempo, etc.
• Media, varianza e deviazione standard: Tre utili statistiche che
possono essere facilmente calcolate e utilizzate per valutare la
bontà di un dataset o confrontare più dataset tra di loro.
La media
• È un indice della tendenza centrale di una distribuzione di
dati.
• La sua implementazione più comune è la media aritmetica
∑
x=
N
x
i =1 i
N
• Esistono alternative più utili nel caso di data set particolari,
quali la media geometrica (utile quando una serie di numeri è
interpretata secondo il loro prodotto e non somma) :
xgeom = N ∏i =1 xi
N
• E la media armonica (utile per i casi in cui la variabile sia
riferita ad un’altra unità (es. velocità, m/s):
⎛ N 1⎞
xarm = N ⎜⎜ ∑i =1 ⎟⎟
xi ⎠
⎝
−1
La varianza
• È una misura della dispersione dei dati attorno al valore
centrale.
• È inversamente legata alla precisione: maggiore è la
varianza minore è la precisione.
• Matematicamente si esprime secondo la formula:
2
(
)
x
−
x
∑i =1 i
N
σ2 =
N
• In realtà, quando il numero di campioni è piccolo (in genere,
minore di 30-40), è necessario correggere la stima, per il
corretto numero di gradi di libertà:
2
(
)
x
−
x
∑i =1 i
N
s2 =
N −1
La deviazione standard
• È la radice quadrata della varianza
• Ha le stesse unità di misura della variabile che si sta
considerando, quindi è più utile per definire l’intervallo di
valori compatibili con la variabile.
2
(
)
x
−
x
∑i=1 i
N
σ=
N
• Anche in questo caso, quando il numero di misure è piccolo è
necessario correggere la stima per il numero opportuno di
gradi di libertà:
2
(
)
x
−
x
∑i=1 i
N
s=
N −1
Deviazione standard relativa
• È un numero adimensionale, che dà conto del contributo
relativo del “segnale” e del “rumore”
RSD =
s
x
• Quando è espressa in percentuale prende il nome di
coefficiente di variazione:
CV = 100 × RSD = 100 ×
s
x
Misure ripetute
• Nel caso il risultato sia l’esito di misure ripetute, è possibile
calcolare anche la deviazione standard associata alla media:
sx =
s
N
• Questa grandezza, in alcuni testi viene definita come errore
standard, anche se si tratta di un’incertezza.
• Ripetere le misure permette di aumentare la precisione di un
fattore !N
• Es: Immaginiamo di misurare la temperatura di un sistema e
di fare 6 misure replicate:
– 78.9 79.2 79.4 80.1 80.3 80.9
– Media = 79.8 Dev. St. = 0.69
Dev.st(media)=0.28
Precisione e accuratezza
• La qualità di un dato analitico può essere espressa in diverse
maniere
• Precisione ed accuratezza sono due concetti chiave
• Precisione esprime l’accordo tra i risultati di prove
indipendenti ottenuti in condizioni stabilite.
• Accuratezza esprime l’accordo tra il risultato ottenuto ed
“un” valore vero del misurando.
• In una situazione ideale i dati dovrebbero mostrare elevata
accuratezza e precisione (un valor medio vicino al “valor
vero” e una minima dispersione).
• Nella pratica si possono verificare 4 tipi di scenari.
Precisione e accuratezza - 2
Precisione e accuratezza - 3
• In molti casi non è possibile ottenere allo stesso tempo
un’elevata precisione e accuratezza e l’attenzione si
focalizza sulla precisione.
accuratezza
xi = µ + esist ,i + ecas ,i
esattezza
precisione
• La mancanza di accuratezza (a rigori di esattezza) può
essere corretta a posteriori (ad es. con un materiale o
metodo di riferimento)
• Una volta raccolti i dati, invece, non si può fare nulla per
compensare la mancanza di precisione.
Determinare la precisione
• Bisogna conoscere la distribuzione dei dati
• Infatti, sebbene la dev.st. dia un’informazione sulla
dispersione dei dati, non dice nulla su come essi siano
distribuiti
• Distribuzione: associare a ciascun valore che può assumere
la grandezza un numero che quantifichi il nostro grado di
fiducia sulla sua realizzazione.
• La distribuzione dei dati può essere ricostruita
sperimentalmente (ma serve un numero sufficiente di misure)
o si può far riferimento a distribuzioni statistiche note.
• Si è visto che gli errori casuali seguono una distribuzione
caratteristica, detta normale o gaussiana.
La distribuzione degli errori
esempio
Combinazioni di 4 incertezze di uguale entità
Combinazione incertezze
Grandezza errore
Numero combinazioni
Frequenza relativa
+U1+U2+U3+U4
+4U
1
1/16 = 0.0625
+2U
4
4/16 = 0.250
0
6
6/16 = 0.375
-2U
4
4/16 = 0.250
-4U
1
1/16 = 0.0625
-U1+U2+U3+U4
+U1-U2+U3+U4
+U1+U2-U3+U4
+U1+U2+U3-U4
-U1-U2+U3+U4
+U1+U2-U3-U4
+U1-U2+U3-U4
-U1+U2-U3+U4
+U1-U2-U3+U4
-U1+U2+U3-U4
+U1-U2-U3-U4
-U1+U2-U3-U4
-U1-U2+U3-U4
-U1-U2-U3+U4
-U1-U2-U3-U4
La distribuzione normale
1
f(x)=
e
2πσ
(
x −µ )2
−
2σ2
m=10 s=3
0.14
m=40 s=3
0.12
0.1
f(x)
0.08
0.06
m=40 s=6
0.04
m=40 s=12
0.02
0
-10
0
10
20
30
40
x
50
60
70
80
90
Proprietà della distribuzione normale
• Dipende esclusivamente dai parametri µ e σ.
• Simmetrica rispetto al valore atteso µ.
Intervallo di confidenza
• È l’intervallo di valori all’interno del quale possiamo
ragionevolmente assumere si trovi il valor vero.
• I valori estremi dell’intervallo sono detti limiti di confidenza.
• Il termine confidenza indica che possiamo associare al
risultato una certa probabilità.
• Data la simmetria della distribuzione, se non specificato
altrimenti, l’intervallo si intende centrato sul valore atteso m.
• Ad es: assumendo una distribuzione normale, il 95% dei
valori della x si troverà nell’intervallo:
µ − 1.96σ < x < µ + 1.96σ
• E nel caso faccia più misure sullo stesso campione:
σ
σ
µ − 1.96
< x < µ + 1.96
N
N
Intervallo di confidenza - 2
µ − 1.96σ < x < µ + 1.96σ
• La probabilità di osservare un valore della x compreso in
questo intervallo è 95%.
• Questa probabilità rappresenta l’area (integrale) della
distribuzione gaussiana calcolata tra i due valori estremi.
• A qualsiasi intervallo, anche non simmetrico posso associare
un valore di probabilità (grado di fiducia, livello di confidenza)
0.07
0.07
0.06
0.06
0.05
0.05
0.04
f(x)
f(x)
0.04
0.03
0.03
0.02
0.02
0.01
0.01
0
-10
0
10
20
30
40
x
50
60
70
80
90
0
-10
0
10
20
30
40
x
50
60
70
80
90
Inferenza
• Il nostro scopo è ricostruire la distribuzione del valore vero,
date le misure effettuate sui nostri campioni.
• L’espressione della distribuzione gaussiana è simmetrica
rispetto allo scambio di x e m.
(
µ − x )2
−
1
2
f (µ) =
e 2σ
2πσ
• Se assumiamo che i dati seguano una distribuzione normale,
per stimare la probabilità che il valor vero della variabile x sia
un determinato valore, è necessario calcolare, a partire dai
dati misurati:
– La media aritmetica
– La deviazione standard
x
s
Inferenza - Esempio
• Immaginiamo di fare 100 misure di una variabile x (ad
esempio, la concentrazione di principio attivo in un formulato)
14
115
12
110
10
x
frequenza
105
8
6
100
4
95
2
90
0
10
20
30
40
50
replica
60
70
80
90
0
90
100
x = 100.2
95
100
105
x
σ = 3.5
1
f (µ) =
e
2π 3.5
(
µ −100.2 )2
−
2 (3.5 )2
110
115
Inferenza – Esempio 2
0.12
Intervallo simmetrico rispetto alla media:
0.1
P(100.2-3.5<m<100.2+3.5)=0.6827
0.08
P(100.2-3*3.5<m<100.2+3*3.5)=0.9973
f(m)
P(100.2-2*3.5<m<100.2+2*3.5)=0.9545
0.06
0.04
0.02
0
70
80
90
100
m
110
120
130
110
120
130
0.12
Se invece volessi sapere la probabilità di
osservare un valore tra 96 e 101:
0.08
f(m)
P(96<m<101)=0.4753
0.1
0.06
0.04
0.02
0
70
80
90
100
m
La distribuzione normale standardizzata
• Al variare dei valori di µ e σ possono esistere ∞2 distribuzioni
normali.
• L’integrazione di questa distribuzione non può darsi in forma
analitica ma richiede un’integrazione numerica.
• È possibile ricondurre tutte le infinite distribuzioni normali ad
un’unica distribuzione, ricorrendo alla trasformazione:
x −µ
z=
σ
• In questo caso, si ottiene una nuova variabile, z, che è
distribuita secondo una distribuzione normale con µ=0 e σ=1.
f(z)=
1
e
2π
−
z2
2
La distribuzione normale standardizzata - 2
0.4
0.35
0.3
f(z)
0.25
0.2
0.15
0.1
0.05
0
-5
-4
-3
-2
-1
0
z
1
2
3
P(-1<z<1)=0.6827
P(-2<z<2)=0.9545
P(-3<z<3)=0.9973
4
5
La distribuzione normale standardizzata - 3
• L’integrale della distribuzione normale standardizzata è
calcolato per via numerica.
• In particolare, la probabilità che z sia minore o uguale ad un
certo valore z* prende il nome di funzione di distribuzione
cumulativa (cdf):
z
( )
z*
z*
−∞
−∞
Φ z* = ∫ f ( z )dz = ∫
1
e
2π
2
−
2
dz
• Per la distribuzione normale standardizzata, questa funzione
assume la forma di una sigmoide e i suoi valori in funzione di
z sono tabulati.
1
0.9
0.8
0.7
phi(z)
0.6
0.5
0.4
0.3
0.2
0.1
0
-5
-4
-3
-2
-1
0
z
1
2
3
4
5
Alcune proprietà della cdf
• Per la simmetria della distribuzione normale,
– P(z<0)=Φ(0)=0.5
– P(z<-z*) =Φ (-z*)=1-P(z<z*)=1-Φ (z*)
con z*>0
• Per le proprietà degli integrali e della probabilità,
– P(a<z<b)=Φ (b)-Φ (a)
• Se invece fossi interessato a conoscere la probabilità che z
assuma un valore maggiore di z*, allora per le proprietà della
probabilità:
– P(z>z*)=1-Φ (z*)
• Dal momento che sono i valori di Φ (o talvolta di 1-Φ ad
essere spesso tabulati, queste uguaglianze sono utili per
poter procedere con l’inferenza.
I valori della cdf
Tabella
z
.0
.1
.2
.3
.4
.5
.6
.7
.8
.9
0.0 .5000 .5398 .5793 .6179 .6554 .6915 .7257 .7580 .7881 .8159
1.0 .8413 .8643 .8849 .9032 .9192 .9332 .9452 .9554 .9641 .9713
2.0 .9772 .9821 .9861 .9893 .9918 .9938 .9953
3.0 .9987 .9990 .9993 .9995 .9997
.996
.9974 .9981
Esempio
• Avete acquistato un elettrodo per la misura del pH con
garanzia di funzionamento di 8000 ± 200 ore (µ ± σ).
• Qual è la probabilità che lo dobbiate cambiare prima di aver
raggiunto le 7500 ore (x) di utilizzo?
• z* = (x-m)/s = (7500 - 8000)/200 = - 2.5
• Dal momento che nella tabella sono riportati solo i valori
positivi, dobbiamo sfruttare la proprietà vista in precedenza:
• P(z<-2.5)=1-P(z<2.5)=1-0.9938=0.0062
• La probabilità che l’elettrodo si rompa prima che siano state
raggiunte le 7500 ore di utilizzo è dello 0.62%
Esempio - 2
• Avete acquistato un elettrodo per la misura del pH con
garanzia di funzionamento di 8000 ± 200 ore (µ ± σ).
• Qual è la probabilità che l’elettrodo si rompa non prima che
siano state raggiunte le 8300 ore (x) di utilizzo?
• z* = (x-m)/s = (8300 - 8000)/200 = 1.5
• In questo caso, voglio conoscere la probabilità:
• P(z>z*)=P(z>1.5)=1-F(1.5)=1-0.9332=0.0668
• La probabilità che l’elettrodo si rompa dopo che siano state
raggiunte le 8100 ore di utilizzo è del 6.68%
Esempio - 3
• Avete acquistato un elettrodo per la misura del pH con
garanzia di funzionamento di 8000 ± 200 ore (µ ± σ).
• Qual è la probabilità che l’elettrodo si rompa tra le 7940 e le
8560 ore (x) di utilizzo?
• In questo caso voglio conoscere la probabilità:
• P(z1<z<z2) con:
• z1 = (x1-m)/s = (7940 - 8000)/200 = -0.3
• z2 = (x2-m)/s = (8560 - 8000)/200 = 2.8
• Per quanto detto in precedenza:
• P(z1<z<z2) = P(z<z2)-P(z<z1)
• P(z<z2) =P(z<2.8)=0.9974
• P(z<z1) =P(z<-0.3)=1-P(z<0.3)=1-0.6179=0.3821
• P(z1<z<z2) =0.9974-0.3821=0.6153
• La probabilità che l’elettrodo si rompa tra le 7940 e le 8560
ore di utilizzo è del 61.53%
La variabile t di Student
• Le considerazioni fatte finora valgono nel caso in cui la
deviazione standard sia nota, o sia stata stimata a partire da
un numero sufficientemente alto di misurazioni.
• Nel caso questo non accada, è necessario tener conto del
fatto che anche la stima della deviazione standard a partire
dai dati è affetta da incertezza.
• Questa incertezza tende a diminuire all’aumentare del
numero di determinazioni effettuate.
• È stato dimostrato che, nel caso in cui la variabile che si
vuole studiare segua una distribuzione normale
standardizzata, la sua stima su un campione reale segue una
distribuzione chiamata t di Student.
La t di Student - 2
t=
x−x
s
n = gradi di libertà= N-1
⎛ ν +1⎞
ν +1
−
Γ⎜
⎟
2
2 ⎠ ⎛ t ⎞ 2
⎝
⎜⎜1 + ⎟⎟
f (t ) =
ν⎠
⎛ν⎞
νπΓ⎜ ⎟ ⎝
⎝2⎠
Alcune proprietà della t di Student
• La distribuzione non dipende da m e s (o dalle loro stime sul
campione statistico).
• È una distribuzione simmetrica e il suo valore atteso è 0
• La sua forma dipende dal numero di misurazioni fatte per
stimare la deviazione standard (correlate al numero di gradi
di libertà)
• Man mano che il numero di misurazioni aumenta, la
distribuzione tende alla distribuzione normale standardizzata
• Anche la t non è integrabile analiticamente, ma richiede
un’integrazione numerica, per cui i valori dei suoi integrali
sono spesso riportati in tabelle apposite.
La t di Student
Interpretare la tabella
• Nella tabella, sono riportati i valori di t* corrispondenti a
particolari percentuali della cdf (una coda).
• Inoltre è considerata la possibilità di definire un intervallo
simmetrico attorno alla media (due code).
• I ragionamenti che si possono fare sono analoghi a quanto
visto per z.
Due code
0.35
0.35
0.3
0.3
0.25
0.25
0.2
0.2
0.15
0.15
0.1
0.1
0.05
0.05
0
-8
-6
-4
-2
Una coda
0.4
f(t)
f(t)
0.4
0
t
2
4
6
8
0
-8
-6
-4
-2
0
t
2
4
6
8
Esempio
• Immaginiamo di aver misurato il pH di una soluzione tampone
e di aver trovato i seguenti valori:
• 11.2 10.7 10.9 11.3 11.5 10.5 10.8 11.1 11.2 11.0
x = 11.02
s = 0.30
s
10 = 0.10
• Avendo fatto 10 misure il numero di gradi di libertà è 9, che
corrispondono a valori di t (a due code) di:
• 1.833 (90%)
• 2.262 (95%)
• 3.690 (99.5%)
Esempio – 2 (dalla t alla variabile)
• Con 9 gdl, la t* corrispondente al 90% di probabilità è 1.833
(due code).
• Questo significa che, al 90%
•
– -t*< t < t*
Ma t = pH − x = pH − 11.0
0.1
s 10
• Quindi
(
x − t* s
)
(90%):
(
)
10 < pH < x + t* s 10 ⇒ 11.02 − 1.833 × 0.10 < pH < 11.02 + 1.833 × 0.10
11.02 − 0.18 < pH < 11.02 + 0.18 ⇒ 10.84 < pH < 11.20
• (95%, t*=2.262):
11.02 − 2.262 × 0.10 < pH < 11.02 + 2.262 × 0.10
11.02 − 0.23 < pH < 11.02 + 0.23 ⇒ 10.79 < pH < 11.25
• (99.5%, t*=3.690):
11.02 − 3.690 × 0.10 < pH < 11.02 + 3.690 × 0.10
11.02 − 0.37 < pH < 11.02 + 0.37 ⇒ 10.65 < pH < 11.39
Esempio - 3
• A partire dagli stessi dati, ma considerando l’approccio ad
una coda, potremmo affermare che:
– Nel caso di 9 gdl, il 90% dei valori di t è inferiore a 1.383, che riportato
nella scala della variabile significa
pH < 11.02 + 0.14 ⇒ pH < 11.16
– C’è una probabilità del 90% che il pH della soluzione non ecceda
11.16
– Analogamente si può procedere se si desidera un valore diverso di
probabilità. t=1.833 se si vuole una probabilità del 95%:
pH < 11.02 + 0.18 ⇒ pH < 11.20
– O t= 3.250 nel caso del 99.5%:
pH < 11.02 + 0.32 ⇒ pH < 11.34
Test statistici
• In molti casi, possiamo essere interessati a verificare se ci sia
differenza tra i valori misurati e valori standard o di riferimento.
• In termini più rigorosi: se la differenza che si osserva tra i
risultati delle misure e i valori di riferimento possa essere
spiegata esclusivamente in termini degli errori casuali.
• Per far questo si adottano dei test, detti test statistici.
• Nell’eseguire un test statistico si valuta la verità di un’ipotesi,
detta ipotesi nulla.
• Il termine “nulla” vuole significare che non vi sia differenza tra
i valori osservati e quelli di riferimento se non quella dovuta al
solo effetto dell’errore casuale.
• Di solito, questa ipotesi è respinta se la probabilità che la
differenza osservata sia dovuta al caso è minore del 5% (ma si
possono scegliere altri valori).
Test statistici - 2
• Questo significa anche che c’è una probabilità del 5% di
trarre conclusioni errate a partire dai dati osservati.
• I test statistici più comunemente usati si dividono in due
categorie:
– Test che valutano l’esattezza (t-test)
– Test che valutano la precisione (F-test)
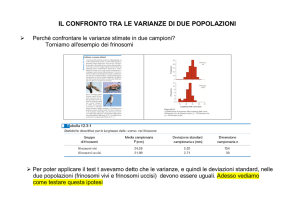
Confronto tra varianze (F test)
• Per confrontare la precisione – e quindi i valori delle varianze
– si impiega un test statistico chiamato F test.
• Il nome deriva dal fatto che la distribuzione di probabilità
associata all’ipotesi nulla prende il nome di distribuzione F di
Fisher.
• Se si vogliono confrontare tra loro due varianze, si costruisce
il rapporto:
s12
2
2
F=
s
2
2
s1 > s2
• dove, per definizione, la varianza numericamente più grande
viene scritta al numeratore.
• Se l’ipotesi nulla è verificata, questo rapporto avrà un valore
prossimo ad 1.
Digressione – la distribuzione F
Rappresenta la distribuzione del rapporto tra due varianze provenienti dalla
stessa popolazione statistica e stimate rispettivamente con n1 e n2 gdl
3.5
(ν1F )
ν1
3
f(F )=
2.5
f(F)
2
v1=1;v2=1
v1=2;v2=2
v1=5;v2=3
v1=3;v2=7
v1=10;v2=10
v1=20;v2=10
v1=30;v2=30
v1=50;v2=50
v1=100;v2=100
ν2
ν2
(ν1F + ν 2 )ν +ν
1
2
⎛ν ν ⎞
FΒ⎜ 1 ; 2 ⎟
⎝2 2⎠
1.5
1
0.5
0
0
0.5
1
1.5
2
2.5
F
3
3.5
4
4.5
5
Confronto tra varianze (F test) - 2
• Il test può essere condotto in due maniere:
– Per verificare se esista una differenza significativa tra le due varianze
(due code).
– Per verificare se una delle due varianze sia sistematicamente
maggiore o minore dell’altra (una coda).
0.6
0.6
0.5
0.5
0.4
0.4
f(F)
0.7
f(F)
0.7
0.3
0.3
0.2
0.2
0.1
0.1
0
0
1
2
3
4
5
F
6
due code
7
8
9
10
0
0
1
2
3
4
5
F
6
7
una coda
8
9
10
Esempio
• Supponiamo di voler verificare se due sintesi per ottenere un
certo prodotto abbiano la stessa precisione.
• Per verificare se la precisione sia la stessa, calcoliamo la F
sperimentale:
s12 1.58
Fsper =
s22
=
1.25
= 1.26
Esempio - 2
0.7
0.6
0.5
f(F)
0.4
0.3
0.2
0.1
0
0
1
2
3
4
5
F
6
7
8
9
10
• La probabilità di osservare, nel caso fosse vera l’ipotesi
nulla, una differenza tra le varianze maggiore di quella
sperimentale è dell’80.6%
• Si può ritenere che la differenza osservata sia legata
all’errore casuale
• Non c’è alcuna significativa differenza tra le due vie
sintetiche.
Esempio - 3
• Interpretazione classica dei test statistici:
– Si costruisce la distribuzione di probabilità associata all’ipotesi nulla
(F)
– Dato il numero di gdl del problema (es. 5,5) si identifica un valore di F
“critico”, corrispondente ad una probabilità fissata, in genere 95%
– Si confronta il valore di F sperimentale con il valore critico
– Se Fsper <Fcrit l’ipotesi nulla viene accettata.
– Nel nostro esempio Fcrit=7.1464 per una probabilità del 95%.
– Fsper=1.26, quindi l’ipotesi nulla è accettata
0.7
0.6
0.5
Fsper
f(F)
0.4
0.3
0.2
0.1
Fcrit
0
0
1
2
3
4
5
F
6
7
8
9
10
F – tabella una via (p=0.05)
F – tabella due vie (p=0.05)
F test - commenti
• Il test F è un modo semplice di confrontare la precisione di due
serie di misure o di due metodi
• Inoltre, molti altri test statistici richiedono come condizione che
le varianze delle serie di misure che si confrontano non siano
statisticamente differenti
• Un esempio è rappresentato proprio dal t test per la valutazione
dell’esattezza, che richiede l’uguaglianza delle varianze.
Confronto dell’esattezza (t-test)
• In tutti i casi in cui si voglia valutare l’esattezza di una serie
di misure o confrontare tra loro due metodi d’analisi è
necessario impiegare un test chiamato t test.
• In particolare ci possono essere tre usi principali del t test:
– Confronto della media su un campione con un valore di riferimento
– Confronto delle medie ottenute su due campioni diversi
– Confronto tra due metodi applicati a campioni diversi
• In tutti i casi, il principio di fondo è lo stesso, cambia
esclusivamente la modalità di calcolo della variabile t.
Confronto di una media con un valore di riferimento
• In molti casi si vuole valutare l’esattezza di un metodo
analitico, confrontando la media dei risultati ottenuti
applicando il metodo stesso su un campione di riferimento,
con il valore per esso certificato.
• Vediamo come procedere in questo caso, attraverso un
esempio.
• Immaginiamo di voler mettere a punto un metodo per la
determinazione del calcio in un campione d’acqua.
• Per valutare l’esattezza, analizziamo un materiale certificato
che contenga Ca in concentrazione 83.0 mg/L
• Sperimentalmente analizziamo 10 aliquote della soluzione di
riferimento con il nostro metodo ed otteniamo:
x = 85.0
s = 0.6
Confronto con un valore di riferimento - 2
• Il t test funziona calcolando il valore di t sperimentale secondo
x − µ 85.0 − 83.0
l’equazione:
t=
=
= 10.5
s
10
0.6 10
• L’ipotesi nulla è che la differenza osservata tra la media dei
valori misurati con il nostro metodo e il valore di riferimento sia
dovuta esclusivamente all’errore casuale.
• Per valutare questa ipotesi, si può procedere calcolando la
probabilità di osservare un valore di t maggiore o uguale al t
sperimentale (in valore assoluto, perché non siamo interessati
al segno della differenza).
• P(t>|tsper| U t<-|tsper|)=2.3x10-6
0.35
0.3
f(t)
0.25
0.2
0.15
0.1
0.05
-t*
-10
t*
-5
0
t
5
10
Confronto con un valore di riferimento - 3
• Anche in questo caso, si può procedere, in alternativa,
seguendo l’approccio più classico ai test statistici.
• Secondo questo approccio, si identifica il valore di t critico
corrispondente a una probabilità del 95% (ovvero ad una
probabilità del 5% che la differenza osservata sia dovuta solo
ad errore casuale), nel nostro caso considerando “due
code”.
• Si confronta il t sperimentale con il t critico (2.2622).
• Se |tsper|<tcrit l’ipotesi nulla viene accettata, altrimenti si rifiuta
0.4
0.35
0.3
f(t)
0.25
0.2
0.15
0.1
tsper
0.05
0
-10
-5
0
t
5
10
Confronto tra due medie
• Questa versione del t test si utilizza, ad esempio, per
confrontare due metodi nei casi in cui un materiale di
riferimento non sia disponibile.
• In questi casi un metodo nuovo si confronta con un metodo di
riferimento.
• In questo caso, a differenza del caso precedente, si dovrà
tener conto del fatto che si hanno due deviazioni standard
(una per metodo)
• Per questo, prima di effettuare il t test bisognerà verificare le
varianze dei due metodi non siano statisticamente differenti
attraverso un t test.
• Anche in questo caso, illustriamo il procedimento con un
esempio.
Confronto tra due medie - esempio
• Immaginiamo di aver messo a punto un metodo per la
determinazione della percentuale di ferro in un minerale e di
voler confrontare i risultati ottenuti con il nuovo metodo con
quelli di un metodo di riferimento.
• Per far questo si analizzano diverse aliquote (in questo
esempio 10 e 10) di un campione contenente ferro con i due
metodi.
• I risultati sono riportati in tabella.
Confronto tra due medie – esempio 2
• Come detto, per poter confrontare tra loro le medie ottenute è
necessario prima assicurarsi che le varianze non siano
statisticamente differenti, attraverso un F test
• Dal momento che l’F critico è 4.09, si può dire che le due
varianze non sono statisticamente differenti e procedere col t
test.
• Visto che le varianze non sono differenti, si possono
raggruppare in quella che si definisce una varianza “pooled”,
attraverso la formula:
2
2
(
)
(
)
n
−
1
s
+
n
−
1
s
1
2
2
s 2pooled = 1
n1 + n2 − 2
Confronto tra due medie – esempio 3
• Nel nostro caso:
s
2
pooled
s pooled = 0.0235 = 0.15
9 × 0.015 + 9 × 0.032
=
= 0.0235
18
• Si costruisce quindi la variabile t sperimentale, secondo:
t sper =
x1 − x2
⎛1 1⎞
s pooled ⎜⎜ + ⎟⎟
⎝ n1 n2 ⎠
1
2
=
6.40 − 6.53
⎛1 1⎞
0.153⎜ + ⎟
⎝ 10 10 ⎠
1
2
= −2.35
• A questo punto, si procede analogamente a quanto visto
nell’esempio precedente, ricordandosi che questa volta il
numero di gradi di libertà è: n1+n2-2
Confronto tra due medie – esempio 4
• Per valutare la significatività statistica della differenza misurata
si calcola la probabilità di osservare un valore di t!|tsper| (due
code).
• Nel nostro caso questa probabilità è 0.0304 (3.04%)
• L’ipotesi nulla viene rifiutata: la differenza di esattezza tra i due
metodi è statisticamente significativa.
0.35
0.3
f(t)
0.25
0.2
0.15
0.1
|tsper|
-|tsper|
0.05
0
-6
-4
-2
0
t
2
4
6
Confronto tra due medie – esempio 5
• Alternativamente, si può stabilire qual è il valore critico di t per
quei gradi di libertà corrispondente al 95% di probabilità.
• Nel nostro caso (due code) tcrit=2.10
• Siccome |tsper|>tcrit, l’ipotesi nulla viene rifiutata.
• La differenza tra le due medie è statisticamente significativa,
ovvero la probabilità che questa differenza sia dovuta ad errori
casuali è inferiore al 5%.
0.4
0.35
0.3
f(t)
0.25
tsper
0.2
0.15
0.1
0.05
tcrit
-tcrit
0
-6
-4
-2
0
t
2
4
6
Confronto tra metodi con campioni differenti
• Talora, per confrontare due metodi si analizzano campioni
differenti.
• In questo caso non è più possibile calcolare media e deviazione
standard delle misure fatte con ciascun metodo perché le
misure non sono repliche dello stesso campione
• Per il confronto statistico tra i due metodi bisogna quindi
utilizzare un altro approccio, chiamato “paired t-test”.
• Con questo approccio, ogni campione è analizzato due volte,
una con ciascun metodo.
• Per ciascun campione si calcola quindi la differenza tra i valori
di = xi ,1 − xi ,2
misurati con i due metodi:
• Una volta analizzati tutti i campioni si calcola la media delle
differenze e la deviazione standard delle differenze:
2
di
(
di − d )
d = ∑i
s
=
∑i
d
N
N −1
Confronto tra metodi con campioni differenti - 2
• Immaginando di aver analizzato dieci campioni (v. tabella) con i
due metodi, si ottengono i valori:
s d = 4.0
d = 0.4
• A partire da questi valori, si costruisce la t sperimentale:
t sper
d −µ
0.4 − 0.0
=
=
= 0.31
sd 10 4.0 10
Confronto tra metodi con campioni differenti - 3
• A partire da questo t sperimentale si può procedere come nei
casi precedenti.
• La probabilità di osservare |t|>|tsper| è 0.7636 (76.36%) quindi
l’ipotesi nulla è accettata.
• Alternativamente si può dire che il tcrit per 9 gdl è 2.26, quindi
siccome |tsper|<tcrit l’ipotesi nulla è accettata.
0.4
0.4
0.35
0.35
|tsper|
-|tsper|
0.3
0.3
0.25
f(t)
f(t)
0.25
0.2
tsper
0.2
0.15
0.15
0.1
0.1
0.05
0.05
-tcrit
0
-6
-4
-2
0
t
2
4
6
0
-6
-4
tcrit
-2
0
t
2
4
6