GRAFICO SPAZIO-TEMPO
Lo strumento con cui si geometrizza il movimento è il Grafico Spazio-Tempo (Grafico P-t), cioè: il Grafico
Spazio-Tempo è quel grafico che riporta sull'asse delle X il tempo (t) e sull'asse delle Y la posizione
del corpo in movimento (P).
Possiamo affermare che il Grafico P-t è l'espressione geometrica del movimento: in altre parole, ciò che in
Fisica appare come movimento in Geometria diventa il Grafico P-t. Posso dire di piu': qualsiasi proprietà
cinematica è esprimibile all'interno del Grafico P-t ; all'opposto, dal Grafico P-t è ottenibile ogni proprietà
cinematica del movimento. Vediamo adesso di mettere in pratica con qualche esempio quello che abbiamo
appena affermato. Come esempio di ciò, in classe abbiamo visto che il movimento uniforme può essere
descritto con una retta in un grafico Spazio-Tempo: dallo studio di tale Grafico siamo riusciti ad ottenere
tutte le informazioni cinematiche (cioè posizioni, tempi e velocità) del corpo in movimento.
Dalla cinematica al Grafico P-t
Come prima cosa, vediamo in che modo disegnare il Grafico P-t -nel caso
particolare del moto uniforme-. In altre parole, impariamo a trasformare in
un oggetto grafico ciò che è movimento uniforme. La cosa essenziale da
tenere a mente è che il Grafico P-t di un moto uniforme è una retta1, non
necessariamente passante per l'origine, cosicché sono necessari due punti
del grafico per poter fare il disegno.
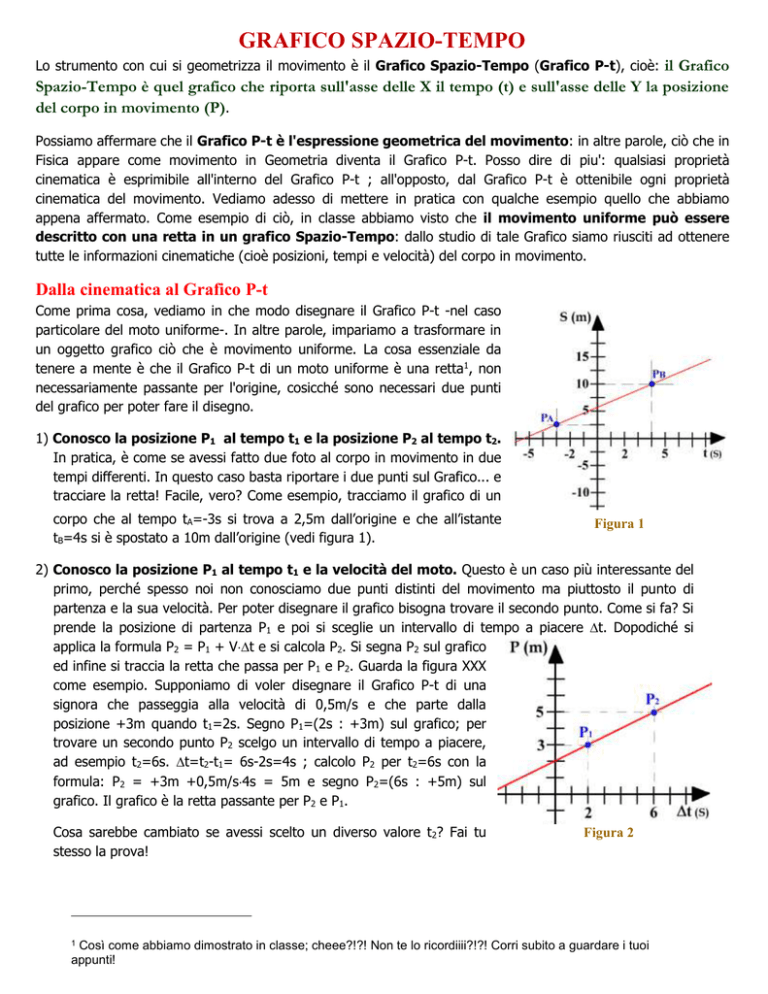
1) Conosco la posizione P1 al tempo t1 e la posizione P2 al tempo t2.
In pratica, è come se avessi fatto due foto al corpo in movimento in due
tempi differenti. In questo caso basta riportare i due punti sul Grafico... e
tracciare la retta! Facile, vero? Come esempio, tracciamo il grafico di un
corpo che al tempo tA=-3s si trova a 2,5m dall’origine e che all’istante
tB=4s si è spostato a 10m dall’origine (vedi figura 1).
Figura 1
2) Conosco la posizione P1 al tempo t1 e la velocità del moto. Questo è un caso più interessante del
primo, perché spesso noi non conosciamo due punti distinti del movimento ma piuttosto il punto di
partenza e la sua velocità. Per poter disegnare il grafico bisogna trovare il secondo punto. Come si fa? Si
prende la posizione di partenza P1 e poi si sceglie un intervallo di tempo a piacere t. Dopodiché si
applica la formula P2 = P1 + Vt e si calcola P2. Si segna P2 sul grafico
ed infine si traccia la retta che passa per P1 e P2. Guarda la figura XXX
come esempio. Supponiamo di voler disegnare il Grafico P-t di una
signora che passeggia alla velocità di 0,5m/s e che parte dalla
posizione +3m quando t1=2s. Segno P1=(2s : +3m) sul grafico; per
trovare un secondo punto P2 scelgo un intervallo di tempo a piacere,
ad esempio t2=6s. t=t2-t1= 6s-2s=4s ; calcolo P2 per t2=6s con la
formula: P2 = +3m +0,5m/s4s = 5m e segno P2=(6s : +5m) sul
grafico. Il grafico è la retta passante per P2 e P1.
Cosa sarebbe cambiato se avessi scelto un diverso valore t2? Fai tu
stesso la prova!
1
Figura 2
Così come abbiamo dimostrato in classe; cheee?!?! Non te lo ricordiiii?!?! Corri subito a guardare i tuoi
appunti!
Dal Grafico P-t alla cinematica
Adesso analizziamo il processo inverso: vedremo come ottenere tutte le informazioni cinematiche dal Grafico P-t.
1) Posizione e tempo di un corpo in movimento. Di per se stesso, il Grafico P-t è la rappresentazione
su assi cartesiani delle diverse posizioni assunte nel tempo dal corpo durante il suo movimento. Perciò io
posso sapere la posizione P1 del corpo conoscendo il tempo t1 o sapere il tempo t2 conoscendo la
posizione P2 direttamente dal grafico.
2) Velocità del movimento. La velocità di un moto uniforme (V0)
coincide con la velocità media: V0=P/t. Perciò per calcolare V0 è
necessario conoscere P e t. Si scelgono due punti qualsiasi sulla
retta, P1 e P2, di cui si misurano le posizioni P1 , P2 e i tempi tA , tB:
infine si calcola P=P1-P2 e t=t1-t2, poi faccio il rapporto. Prendi
come esempio la figura 3: scelgo sulla retta i due punti P1=(-30s : 75m) , P2=(60s : 50m). Calcoliamo P e t:
P = P2 – P1 = 50m – (-75m) = 125m
t = 60s – (-30s) = 90s
V0 = P/t = 125m/90s = 1,39 m/s
Figura 3
Cosa cambia se invece di P1 e P2 avessi scelto altri due punti?
Nota bene che la formula V0=P/t mostra che la velocità coincide con il coefficiente angolare
della retta (m) del Grafico P-t. La dimostrazione di questa fondamentale proprietà è data in
Appendice.
3) Moto uniforme. Fino ad ora abbiamo mostrato con esempi che il grafico P-t di un moto uniforme è una
retta. Non abbiamo però mostrato la proprietà inversa, cioè che se il grafico del moto è una retta allora il
moto è uniforme. La proprietà inversa può essere immediatamente dimostrata usando il punto 2),
quando si afferma che la velocità è il coef. angolare della retta. Ecco la dimostrazione: <<Poiché il
moto è uniforme allora la velocità è costante e dunque il coef. angolare del grafico è
costante. Ma l'unica figura geometrica ad avere coef. angolare costante è la retta il grafico
di un moto uniforme e' una retta. C.V.D. >>
4) Passaggio per l'origine. In un grafico P-t l'origine e' rappresentata dalla retta P=0 , cioè dall'asse di t
(asse X). Il tempo del passaggio per l'origine è perciò l'intercetta della retta con l'asse t.
5) Posizione al tempo "0". In un grafico P-t il tempo t=0 è dato dall'asse delle P (Y). La posizione al
tempo t=0 è perciò data dall'intercetta con l'asse P.
EQUAZIONE ORARIA - EQUAZIONE DELLA RETTA
Per equazione oraria si intende quell'equazione che associa al tempo "t" la posizione "P" assunta
dal corpo al tempo “t”
In altre parole, l'eq. oraria è quell'equazione che permette di calcolare S conoscendo t.
L'equazione oraria di un moto uniforme è facilmente ricavabile dall'equazione della retta del grafico P-t: ecco
come si fa.
Il grafico di una retta è dato dall'equazione:
Y = mX + q
(1)
Nel grafico P-t si ha che: X = t ; Y = P ; m = V0 ; per quanto riguarda "q", esso è il valore dell'intercetta
sull'asse delle Y, che nel grafico P-t corrisponde al valore dell'intercetta sull'asse delle P e dunque coincide con.....
(guarda gli appunti sopra, sfaticato!), che indichiamo con P(0). Sostituendo nell'eq. (1) ottengo:
P2 = V0t + P1
(2) , che e' l'eq. oraria richiesta.
Esempio: il moto di figura 2 ha velocità V0=1,39m/s
(come già calcolato sopra) ed intercetta l’asse Y nel
punto Y=-33,33m (come di evince dal grafico). Ne segue
che la retta ha equazione Y = 1,39X - 33,33 ; dunque la
sua eq. oraria è: P2 = 1,39t – 33,33m .
Un altro esempio di equazione oraria ottenuta sfruttando
il Grafico P-t è descritto in figura 4.
Figura 4
APPENDICE
La velocità di un moto uniforme è il coef. angolare della retta nel Grafico P-t
In questa Appendice voglio dimostrare che il coef. angolare della retta del Grafico P-t coincide con la velocità. Per
dimostrarlo, partiamo dalla definizione di coef. angolare, così come è data in Matematica e in Geometria.
Definizione Matematica e Geometrica di “m”
Generalmente il coefficiente angolare di una retta (m) viene definito attraverso la cosiddetta equazione
generica della retta:
aX + bY + c = 0
(I)
, con a , b , c tre coefficienti numerici, diversi da retta a retta.
Dalla (I) si ottiene subito:
Y = -a/bX - c/b , b 0
Alla frazione -a/b viene dato il nome di coef. angolare (m) mentre la frazione -c/b ha il nome di termine noto
(q), cosicchè l'eq. (I) si scrive:
Y = mX + q
(II)
Posso perciò dare una definizione matematica di “m”:
il coef. angolare “m” di una retta e' il rapporto -a/b dei coefficienti dell'equazione della retta
generica
Questa definizione è facile da comprendere ma ha una debolezza: è fine a se stessa, cioè non porta praticamente
a nulla. Quello che a noi ci serve è una definizione geometrica di m: attraverso di essa vedremo che in un
moto uniforme il valore di m coincide con la velocità.
Il modo migliore per dare la definizione geometrica di m è quello di partire dal suo calcolo. Scriviamo di nuovo
l'eq. (II):
Y = mX + q
Per calcolare m consideriamo due punti sulla retta, PA=(XA : YA) e PB=(XB : YB) ; vedi ad esempio la coppia di
punti di figura 2. Entrambi i punti appartengono alla retta e perciò le loro coordinate devono soddisfare
rispettivamente all'equazione:
YA = mXA + q
(III)
YB = mXB + q
(IV)
Ho un sistema con 2 equazioni e 2 incognite (m , q) che posso risolvere usando il metodo.... "della sostituzione”!
Dalla seconda equazione ottengo “q” che poi..."
"Silenzio! Avete sbagliato."
"?!? Prof, come è che si è
sbagliato? Il metodo della sostituzione non sbaglia mai!" Verissimo, il metodo della sostituzione non sbaglia
mai... ma in questo caso conviene usare un metodo diverso, che permette di evidenziare subito le proprietà
geometriche di m: quello della differenza membro a membro.
Infatti, se da (IV) sottraiamo (III) otteniamo: YB-YA = m(XB-XA) [il termine q si cancella da sé]
m = (YB-YA)/(XB-XA) = Y/X
(V)
Il rapporto Y/X ha il nome di rapporto incrementale o pendenza. Perciò posso affermare che:
il coefficiente angolare “m” di una retta è il suo rapporto incrementale (la sua pendenza)
Questa enunciata sopra è la definizione geometrica del coef. angolare (che poi è anche la sua definizione in
assoluto più importante).
In un moto uniforme, la pendenza del grafico P-t corrisponde al valore della velocità
Adesso siamo in grado di dimostrare con un semplice passaggio ciò che cercavamo, cioè dimostrare che il coef.
angolare “m” del grafico di un moto uniforme rappresenta la velocità
Tenendo conto che in un Grafico P-t : Y=P , X=t , sostituendo nell'eq. (V).... continua tu la dimostrazione!












