Generatore d'onda quadra
Il generatore d'onda quadra è un circuito che fornisce in uscita un'onda quadra, senza
che vi sia alcun segnale d'ingresso. Questo circuito viene anche detto oscillatore a
rilassamento o multivibratore astabile.
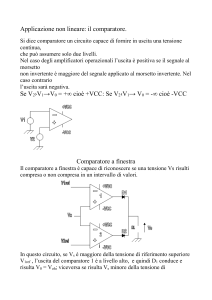
Un circuito generatore d'onda quadra con amplificatore operazionale è riportato in
figura.
Per studiare un circuito con amplificatore operazionale dovremo tenere conto
dell'equipotenzialità degli ingressi e che gli ingressi non assorbono corrente.
La capacità C si carica e si scarica attraverso la resistenza R verso il valore della
tensione d'uscita, con costante di tempo τ = RC .
In tale circuito è presente una rete di retroazione positiva che fissa il valore dell'ingresso
V+ in dipendenza del valore della tensione d'uscita. La tensione d'uscita può assumere
solo due valori: VoH e VoL , tensioni di saturazione, cui corrispondono le due tensioni
V+ H e V+ L , definite come:
V+ H =
R2
⋅ VoH
R1 + R 2
V+ L =
e
R2
⋅ VoL
R1 + R 2
V+ H e V+ L sono le tensioni di soglia in corrispondenza delle quali commuta l'uscita,
allorché la tensione sulla capacità, che si carica attraverso la resistenza R al valore della
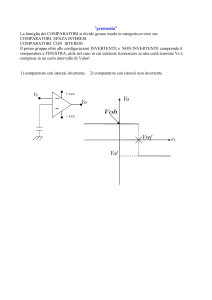
tensione d'uscita, uguaglia tali valori. L'amplificatore operazionale e il partitore R 1 R 2 ,
rispetto alla tensione sull'ingresso invertente (tensione VC ai capi della capacità), si
comportano da comparatore con isteresi invertente, le cui tensioni di soglia sono V+ H e
V+ L e la tensione d'ingresso è la tensione sull'ingresso invertente, coincidente con la
tensione sulla capacità, V− = VC . La caratteristica d'uscita è la seguente:
VoH
V+ L
VoL
Vo
V+ H
VC
Supponendo che la tensione d'uscita abbia appena commutato a livello alto VoH , perché
la tensione sulla capacità ha uguagliato la tensione V+ L , la capacità inizierà a caricarsi
verso la tensione d'uscita VoH attraverso la resistenza R (con costante di tempo
τ = RC ) partendo dalla tensione V+ L .
Vo ; VC
VoH
V+ H
t1
t2
t
V+ L
VoL
T1
T2
T
Quando, dopo un tempo t = t 1 = T1 , la tensione VC raggiunge il valore V+ H ,
prevalendo l'ingresso invertente su quello non invertente, l'uscita commuta dal valore
VoH al valore VoL , interrompendo la carica della capacità che, partendo dal valore
V+ H , inizia a caricarsi verso VoL . Quando, dopo un tempo t = t 2 − t 1 = T2 , la tensione
VC raggiunge il valore V+ L , prevalendo l'ingresso non invertente su quello invertente,
l'uscita commuta dal valore VoL al valore VoH , interrompendo la carica della capacità
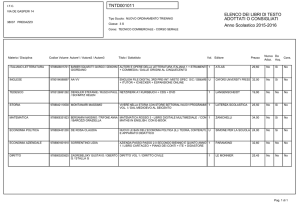
che, partendo dal valore V+ L , inizia a caricarsi verso VoH . E il ciclo si ripete, generando
in uscita un'onda quadra, come mostrato nel grafico.
Calcolo del semiperiodo T1
Per calcolare la durata T1 , del primo semiperiodo, bisogna scrivere l'equazione di carica
della capacità a partire dal tempo t = 0 e imporre che al tempo t = t 1 = T1 assuma il
valore V+ H .
VC (t ) = Vf + (Vi − Vf ) ⋅ e
−
t
τ
= VoH + (V+ L − VoH ) ⋅ e
−
t
τ
dove τ = RC
Si impone che al tempo t = t 1 = T1 sia:
VC (t 1 ) = VoH + (V+ L − VoH ) ⋅ e
⇒ −
V − VoH
T1
= ln + H
τ
V+ L − VoH
Supponendo che sia
−
T1
τ
= V+ H ⇒ e
⇒ T1 = − τ ln
−
T1
τ
=
V+ H − VoH
V+ L − VoH
⇒
V+ H − VoH
V − VoH
= τ ln + L
V+ L − VoH
V+ H − VoH
VoH = − VoL ⇒ V+ H = − V+ L ,
ed essendo
V+ H =
R2
R2
⋅ VoH = −
⋅ VoL = − V+ L ,
R1 + R 2
R1 + R 2
si ha:
T1 = τ ln
V+ L − VoH
V+ H − VoH
R2
− R 2 − R1 − R 2
⋅ VoH − VoH
R1 + R 2
R1 + R 2
= τ ln
= τ ln
=
R 2 − R1 − R 2
R2
⋅ VoH − VoH
R1 + R 2
R1 + R 2
−
= τ ln
⎛
R 1 + 2R 2
2R 2
= τ ln⎜⎜ 1 +
R1
R1
⎝
⎞
⎟⎟ = T1
⎠
Calcolo del semiperiodo T2
Per calcolare la durata T2 , del secondo semiperiodo, bisogna scrivere l'equazione di
carica della capacità a partire dal tempo t − t 1 = 0 e imporre che al tempo
t = t 2 ⇒ t 2 − t 1 = T2 assuma il valore V+ L .
VC (t ) = Vf + (Vi − Vf ) ⋅ e
−
t − t1
τ
= VoL + (V+ H − VoL ) ⋅ e
−
t −t1
τ
dove τ = RC
Si impone che al tempo t = t 2 ⇒ t 2 − t 1 = T2 sia:
VC (t 2 ) = VoL + (V+ H − VoL ) ⋅ e
⇒ −
V − VoL
T2
= ln + L
τ
V+ H − VoL
−
T2
τ
= V+ L ⇒ e
⇒ T2 = − τ ln
−
T2
τ
=
V+ L − VoL
V+ H − VoL
V − VoL
V+ L − VoL
=
= τ ln + H
V+ L − VoL
V+ H − VoL
R2
⋅ VoL − VoL
⎛
R1 + R 2
R + 2R 2
2R 2
= τ ln
= τ ln 1
= τ ln⎜⎜ 1 +
R2
R1
R1
⎝
⋅ VoL − VoL
R1 + R 2
−
⇒
⎞
⎟⎟ = T2
⎠
Poiché i due semiperiodi sono uguali, T1 = T2 , il circuito genera un'onda quadra di
⎛
2R 2
periodo T = 2τ ln⎜⎜ 1 +
R1
⎝
⎞
⎟⎟ .
⎠
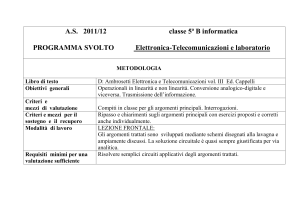
Se si vuole un'ampiezza della tensione d'uscita diversa dalla tensione di saturazione si
possono aggiungere in uscita due diodi zener in antiserie, come in figura.
Questa modifica non comporta alcuna variazione del funzionamento del circuito, purché
la corrente Iz non assuma valori tali da far intervenire il circuito di limitazione della
corrente d'uscita.
L'ampiezza della tensione d'uscita sarà uguale a VZ + Vγ
Il valore della resistenza R Z si calcola, una volta fissato il valore della corrente I Z , nel
seguente modo:
RZ =
Vo1H − (VZ + Vγ )
IZ
Nel caso si vuole ottenere un'ampiezza della tensione d'uscita variabile, si può utilizzare
un potenziometro e un amplificatore operazionale in configurazione di inseguitore,
come in figura.
Il potenziometro R P , di valore opportunamente alto, è il carico fisso per il circuito
generatore d'onda quadra, la tensione ad onda quadra viene fornita tramite l'inseguitore
che presenta una resistenza d'uscita praticamente nulla.