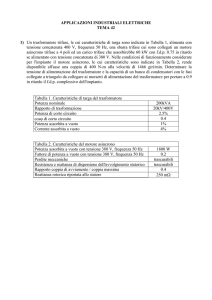
Progetto e dimensionamento di massima di un convertitore e del
relativo trasformatore di alimentazione.
Tipo:
monofase
N1
controfase
non controllato
Lf
D1
N22
I1
Vu
V21
R
V1
V22
N22
D2
Linea di ingresso: linea di alimentazione monofase V =220 V, f =50 Hz
Carico:
puramente resistivo
R =80 Ω
Potenza media al carico Pm =200 W
Ipotesi:
diodi ideali
Induttanza di filtro Lf tale da poter ritenere la corrente nel carico
priva di armoniche
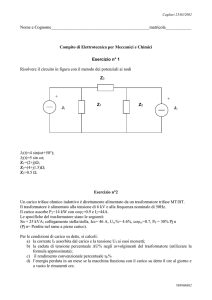
Calcolo della tensione media al carico:
Vm =
π
Vpk
1
1
2
π
(cos 0 − cos π ) = Vpk = 0.6366Vpk
Vpk sin(ωt ) d (ωt ) = Vpk [− cos(ωt )]0 =
∫
π 0
π
π
π
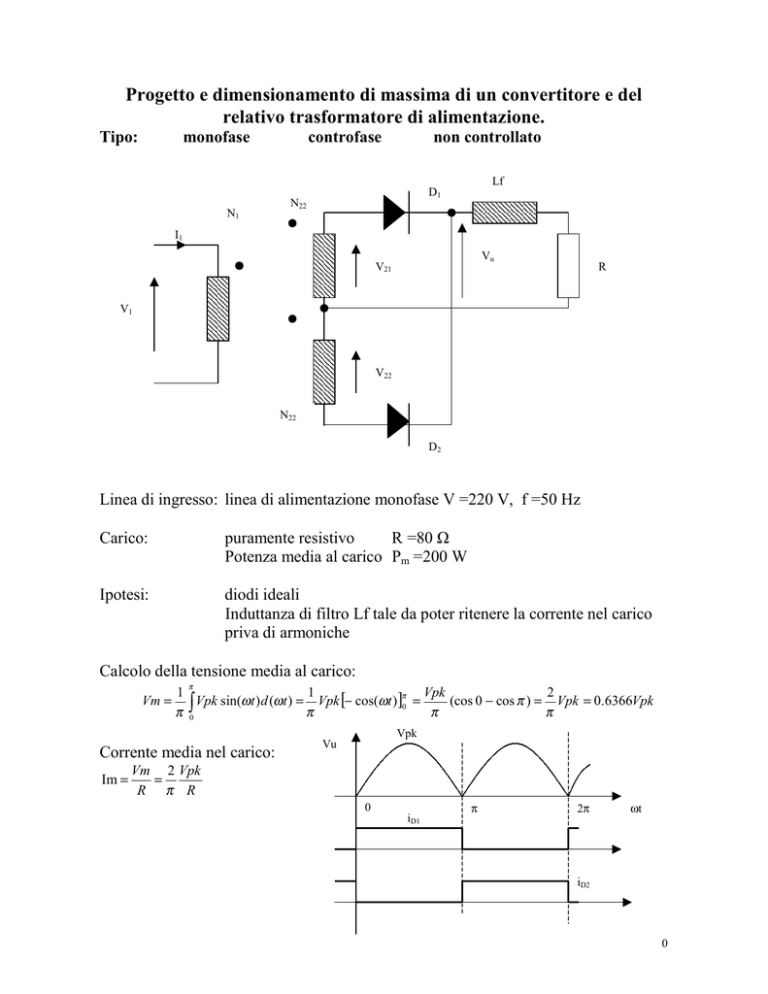
Corrente media nel carico:
Im =
Vpk
Vu
Vm 2 Vpk
=
R π R
0
iD1
π
2π
ωt
iD2
0
Potenza media dissipata nel carico:
Pm = Vm Im =
2
2
1
4 Vpk 2
Vpk ⋅ Vpk = 2
π
π
R π
R
N.B. espressione valida in quanto è stata ipotizzata l’assenza di armoniche nella
corrente di carico.
Tensione in uscita al trasformatore:
Vpk =
R ⋅ Pm ⋅ π 2 π
=
4
2
R ⋅ Pm =
π
80 ⋅ 200 = 198.7V
2
cui corrisponde un valore efficace di:
V2=
Vpk
2
=
198.7
2
= 140.5V
Dimensionamento dei diodi del convertitore:
Valore medio della corrente in un diodo:
ID1m =
Im 2 Vpk 1 Vpk 198.7
=
=
=
= 0.79 A
2 π R 2 πR π ⋅ 80
Valore efficace della corrente in un diodo:
ID1 =
Im
2 Vpk
Vpk
198.7
=
= 2
= 2
= 1.12 A
πR
π ⋅ 80
2
2 πR
Fattore di forma della corrente in un diodo:
KfID =
ID1 Im 2
=
= 2 = 1.414
ID1m
2 Im
Massima tensione di polarizzazione inversa dei diodi:
Vipk = 2 ⋅ Vpk = 2 ⋅ 198.7 = 397.4V
Dimensionamento del trasformatore di alimentazione:
Si considera il trasformatore come costituito da un avvolgimento primario avente N1
spire e due avvolgimenti secondari aventi ciascuno N21=N22 spire.
1
Calcolo del rapporto spire del trasformatore:
2 ⋅ 220
N1
N 1 V 1 V 1 pk
=
=
=
=
= 1.57
198.7
N 21 N 22 V 21 V 2 pk
Potenza di dimensionamento di un avvolgimento secondario del trasformatore
( N21 spire ):
A21 = V 21 ⋅ I 21 = V 21 ⋅ ID1 =
Vpk Im π
1
π
π
π
1
⋅
= Vm
= ⋅ Vm ⋅ Im = Pm = ⋅ 200 = 157VA
Im
4
4
2 4
2
2 2
2
Potenza di dimensionamento del secondario del trasformatore:
A2 = 2 A21 = 2
π
π
π
Pm = Pm = ⋅ 200 = 314VA
4
2
2
Potenza di dimensionamento del primario del trasformatore:
AI = V 1 ⋅ I 1 = V 1 ⋅ Im
π
π
N 21
N1
N 21 Vpk
= V 21
⋅ Im
=
Im =
Vm ⋅ Im =
200 = 222VA
N1
N 21
N1
2
2 2
2 2
Potenza di dimensionamento del trasformatore:
π
π
+
AI + AII 2 2 2
π
1
A=
Pm = 1 +
=
Pm = 1.34 Pm = 1.34 ⋅ 200 = 268VA
2
2
4
2
Verifica della potenza assorbita al primario del trasformatore:
Analisi armonica della corrente assorbita al primario:
2
Vpk
V1
V 1(ωt ) = V 1 pk ⋅ sin(ωt ) = 2 ⋅ V 1 ⋅ sin(ωt )
0
+
I 1(ωt ) =
−
N 21
Im
N1
per 0 ≤ ωt ≤ π
N 21
Im
N1
per π ≤ ωt ≤ 2π
π
ωt
2π
I1
N 21
Im
N1
ωt
periodo 2π corrispondente per f=50 Hz a 20 ms.
N.B. Sviluppo armonico di una funzione con f.d.o. quadra e periodo 2π di
ampiezza unitaria
A0= valore medio
1
A1pk = ampiezza dell’armonica di ordine 1
π
0
2π
A1 = valore efficace dell’armonica di ordine 1
-1
La funzione è una funzione dispari ⇒ sono presenti unicamente i termini
del tipo Ak Sin(kωt)
π
π
2
2
2
4
A1 pk = ∫ 1 ⋅ sin(ωt )d (ωt ) = [cos(ωt )] = (cos(0) − cos(π ) ) =
π 0
π
π
π
0
A1 = A1 pk
1
2
=
4
2π
=
2 2
= 0.9
π
di conseguenza il valore efficace della componente di prima armonica della corrente
in ingresso al trasformatore risulterà:
I 1 A1 =
N 21
2 2
Im
π
N1
la corrente media nel carico risulta:
Im =
Vm
=
R
Pm
= ID1m ⋅ 2 = 0.79 ⋅ 2 = 1.58 A
R
3
ωt
da cui:
I 1 A1 =
N 21
2 2
1
2 2
=
⋅ 1.58 ⋅
= 0.91A
Im
N1
1.57
π
π
Potenza assorbita al primario del trasformatore
Dai diagrammi delle tensioni e delle correnti al primario si verifica che lo sfasamento
tra le prime armoniche della tensione e della corrente è nullo.
P1 =
V 1 pk
2
I 1 A1 =
V 21 pk N 1 N 21
2 2
2
⋅
= Vpk Im = Vm ⋅ Im = 200W
Im
π
π
2 N 21 N 1
Potenza apparente al primario del trasformatore:
V 1 pk N 21
V 21 pk N 1 N 21
V 21 pk
⋅
Im =
Im =
Im =
2 N1
2 N 21 N 1
2
π
π
π
Vm ⋅ Im =
Vm ⋅ Im =
=
200 = 222VA
2 2
2 2
2 2
S1 = V 1 ⋅ I 1 =
Potenza reattiva al primario del trasformatore:
Essendo nullo lo sfasamento tra tensione e corrente la potenza reattiva è nulla.
Potenza deformante al primario del trasformatore:
D1 = S 1 2 − P1 2 = 222 2 − 200 2 = 96.3VA
4
Progetto e dimensionamento di massima
di un convertitore e del relativo trasformatore di
alimentazione
Tipo:
monofase
ponte
non controllato
D1+
I1
I2
V1
ID1+
V2
ID1-
D1-
Lf
D2+
Vu
R
D2-
Linea di ingresso: idem
Carico: idem
Ipotesi: idem
Calcolo della tensione media al carico:
Vm =
π
1
2
VpkSin(ωt )d (ωt ) = Vpk = 0.6366Vpk
∫
π 0
π
Corrente media nel carico:
Im =
Vm 2 Vpk
=
=
R π R
Pm
200
=
= 1.58 A
R
80
Tensione in uscita al trasformatore
Pm
= R ⋅ Pm = 80 ⋅ 200 = 126.49V
Im
π
π
V 2 pk = Vm = 126.49 = 198.7V
2
2
V 2 pk 198.7
=
= 140.5V
V2=
2
2
Vm =
5
Dimensionamento dei diodi del convertitore:
Valore medio della corrente in un diodo
ID1m =
Im 2 Vpk 1 Vpk 198.7
=
=
=
= 0.79 A
2 π R 2 πR π ⋅ 80
Valore efficace della corrente in un diodo:
ID1 =
Im
2
=
2 Vpk
Vpk
198.7
= 2
= 2
= 1.12 A
πR
π ⋅ 80
2 πR
Fattore di forma della corrente in un diodo:
KfID =
ID1 Im 2
=
= 2 = 1.414
ID1m
2 Im
Dimensionamento del trasformatore di alimentazione:
Calcolo del rapporto spire del trasformatore:
2 ⋅ 220
N 1 V 1 V 1 pk
=
=
=
= 1.57
198.7
N 2 V 2 V 2 pk
Potenza di dimensionamento del secondario del trasformatore:
Analisi della corrente nel secondario del trasformatore:
i 2(t ) = iD1 + (t ) − iD1 − (t )
Valore efficace della corrente nel secondario del trasformatore:
I 2 = Im = 1.58 A
A2 = V 2 I 2 =
V 2 pk
2
Im =
π
2 2
Vm Im =
π
2 2
Pm =
π
2 2
200 = 222VA
V2
0
π
2π
ωt
Im
Im
iD1+(t) , iD2-(t)
iD1-(t) , iD2+(t)
ωt
ωt
Im
i2(t)
ωt
6
Potenza di dimensionamento del primario del trasformatore:
A1 = V 1I 1 =
π
π
N1
N2
V2
I 2 = A2 =
Pm =
200 = 222VA
N2
N1
2 2
2 2
Potenza attiva, reattiva, apparente assorbita al primario del trasformatore:
il calcolo è analogo a quanto effettuato per il convertitore monofase, controfase non
controllato e pertanto viene importato solamente il risultato finale:
P1 = Vm Im = 200W
S 1 = V 1I 1 = 222VA
Q1=0
D1 = S 1 2 − P1 2 = 96.3VA
7
Analisi del funzionamento di un convertitore monofase a
ponte totalcontrollato.
Lf
T1+
T2+
I1
Vc
A
Vu
R
B
T1-
T2-
Analisi della forma d’onda della tensione Vu in uscita al convertitore al variare
dell’angolo di ritardo dei segnali di impulso ai tristori.
Ipotesi: i tristori vengono impulsati con un unico angolo di ritardo α
VAB(t)=VEA(t)
Vu(t)
VAB(t)
0
π
2π
α=0
ωt
3π
α=20°
α=20°=(20/360)*2π rad
ωt
α=π/2
α=π/2
ωt
8
α=150°
α = 150° =
30 * 5
5
π= π
360
6
α=π
Determinazione delle caratteristiche principali della tensione Vu(t):
• Periodo [0,π] equivalenti a 10 ms per f= 50Hz.
• Valore medio variabile al variare dell’angolo di ritardo α.
Determinazione del valore medio di tensione fornito dal convertitore.
Si consideri la seguente forma d’onda:
Vm =
=
1
π
π +α
π +α
∫ VpkSin(ωt )d (ωt ) = Vpk [− cos(ωt )]
α
α
=
Vpk
[cos α − cos(π + α )] = Vpk (cos α + cos α ) =
π
π
2
2 2
Vpk cos α =
V cos α = 0.9V cos α
π
π
cos(π + α ) = − cos α
Vpk
ωt
α
π
π+α
9
Caratteristica tensione media in uscita in funzione dell’angolo di ritardo all’impulso:
2/π Vpk
π/2
π
0
α
-2/π Vpk
Calcolo dell’ angolo di ritardo all’accensione per ottenere con:
• Linea di ingresso: linea di alimentazione monofase V=220 V f=50 Hz
• Carico: carico puramente resistivo R=80 Ω
Una potenza media al carico Pm=200 W
Con l’ipotesi che:
l’induttanza di filtro Lf sia tale da potere ritenere trascurabili le armoniche nella
corrente di carico.
Valore medio di tensione ai capi del carico:
Vm2
Pm =
R
Vm =
relazione valida unicamente in assenza di armoniche di tensione.
R ⋅ Pm =
80 ⋅ 200 = 126 . 5V
Determinazione dell’angolo di ritardo all’accensione:
2 2
V cosα = Vm
π
Vm π
126.5 π
= cos −1
= 50.3° = 0.878rad
α = cos −1
V 2 2
220 2 2
Dimensionamento dei tiristori costituenti il ponte:
Nota: i tiristori costituenti il ponte devono essere dimensionati per il caso più
10
gravoso di funzionamento nell’intervallo 0 ≤ α ≤ π.
Calcolo dei massimi valori di corrente dei tiristori
La condizione più gravosa per quanto riguarda le correnti è la condizione di
funzionamento con α = 0, ciò corrisponde al massimo valore della tensione di uscita.
Per α = 0
Vm (α ) =
2
2
Vpk = 220 2 = 198
π
π
Corrente media nel carico Im =
Vm 198
=
= 2 .475 A
R
80
Corrente media nei tiristori IT 1m =
Corrente efficace nei tiristori
Im 2.475
=
= 1.2375 A
2
2
IT 1 =
Im 2 .475
=
= 1 .75 A
2
2
Fattore di forma della corrente nei tiristori
Kf =
IT 1m Im 2
=
=
IT 1
2 Im
2 = 1 .414
Calcolo della massima tensione di polarizzazione
Trattandosi di tiristori deve essere considerata la massima tensione di polarizzazione
diretta ed inversa sul componente.
Per la configurazione di circuito considerata risulta:
V id pk = Vpk =
2 * 220 = 311 V
Determinazione della potenza assorbita dalla rete per il caso in oggetto
Componente fondamentale della corrente di linea
Dall’analisi della forma d’onda della corrente di linea può essere facilmente
individuabile il valore e la fase della componente fondamentale.
I 1 A1 pk = Im
4
2 2
2 2 1.423 A
⇒ I 1 A1 = Im
= 1.58
= 1.58 A
1.75
π
π
π
espressione della tensione e componente fondamentale della corrente di linea come
funzioni temporali
11
α=50°.3
0
π
2π
ωt
3π
iT1+ , iT2Im
iT2+ , iT1-
Im
i1 = iT1+-iT1-
Componente fondamentale della
corrente di linea
Tensione
Ve (t ) = 2Ve sin(ω t )
Corrente
i1(t ) = 2 I 1 A1 sin(ωt + α )
Corrispondente diagramma dei fasori:
α
Potenza attiva assorbita:
P = Re (V e ⋅ I * 1 A1) = VeI 1 A1 cos α =
= (Vpk
_
V1
_
I1
Vpk
2 2
Im
cos α =
π
2
2
cos α )(Im) = Vm Im = Pm = 200W
π
Potenza reattiva assorbita:
2 2
2
sin α
=
sin α = Vpk cos α Im
π
π
cos α
2
= Vm ⋅ Im⋅ tgα = Pm ⋅ tgα = 200 ⋅ tg 50.3° = 241Var
Q = Im(V e ⋅ I * 1 A1) = VeI 1 A1 sin α =
Vpk
Im
12
Potenza apparente assorbita:
S = Ve ⋅ I 1 = Ve ⋅ Im = 220 ⋅1.75 = 385VA
Determinazione della potenza deformante assorbita:
D = S 2 − P 2 − Q 2 = 3852 − 2002 − 2412 = 224VA
13
Analisi del funzionamento di un convertitore
monofase a ponte semicontrollato
Si considera la struttura “asimmetrica” in quanto non manifesta problematiche di
“perdita di controllo”.
Lf
D2+
T1+
I1
Ve
A
Vu
R
B
T1-
D2-
Analisi della forma d’onda della tensione Vu in uscita al convertitore al variare
dell’angolo di ritardo dei segnali di impulso ai tristori.
Ipotesi: i tiristori vengono impulsati con un unico angolo di ritardo α.
VBA(t)= -VAB(t)
Vu(t)
0
π
VAB(t)
2π
α = 20°
3π
α=0
ωt
α = 20° =(20/360)*2π rad
ωt
α = π/2
α=π/2
ωt
14
α=150°
ωt
α=π
ωt
Determinazione delle caratteristiche principali della tensione Vu(t):
• Periodo [0,π] equivalenti a 10 ms per f = 50 Hz.
• Vu(t) ≥ 0 ∀ t a causa del “diodo equivalente” di ricircolazione.
• Valore medio della tensione variabile in funzione dell’angolo α.
Determinazione del valor medio di tensione fornito dal convertitore
Si consideri la seguente forma d’onda:
π
π
Vpk
1
[− cos(ωt )] = Vpk [cosα − cosπ ] = (1 + cosα )Vpk
Vu = ∫ Vpk sin(ωt )d (ωt ) =
πα
π
π
π
α
α
π
0
2π
3π
π
Caratteristica tensione media in uscita in funzione dell’angolo di ritardo all’impulso
2/π Vpk
Vp/π
0
π/2
π
α
15
Calcolo dell’angolo di accensione per ottenere con:
• Linee di ingresso: linea di alimentazione monofase V = 220 V f = 50 Hz
• Carico : carico puramente resistivo R = 80 Ω
Una potenza media al carico Pm = 200 W
Con l’ipotesi che:
l’induttanza di filtro Lf sia tale da potere ritenere trascurabili le armoniche nella
corrente di carico.
Valore medio della tensione ai capi del carico:
Pm =
Vm
R
2
Relazione valida unicamente in assenza di armoniche di
corrente
Vm = Pm ⋅ R = 200 ⋅ 80 = 126.5V
Determinazione dell’angolo di ritardo di accensione:
Vm =
π ⋅ Vm
Vpk
π ⋅ 126.5
(1 + cos α ) ⇒ α = cos −1
− 1 = cos −1
− 1 = 73.9° = 1.29rad
π
2 ⋅ 220
Vpk
Dimensionamento dei componenti elettronici di potenza costituenti il ponte
Nota: i componenti devono essere dimensionati per il caso più gravoso di
funzionamento nell’intervallo 0 ≤ α ≤ π
Calcolo dei valori massimi di corrente nei diodi e nei tiristori
Tiristori
Per quanto riguarda i tiristori la condizione più gravosa di funzionamento è con
α = 0 , ciò corrisponde al massimo valore della tensione in uscita
per α = 0
Vm(α ) =
1
1
Vpk (cosα + 1) =
2 ⋅ 220(1 + cos 0°) = 198V
π
π
16
Vm 198
=
= 2.475A
80
R
Corrente media nel carico
Im =
Corrente media nei tiristori
IT1 + m =
Corrente efficace nei tiristori I T 1 + =
Im 2.475
=
= 1.2375A
2
2
Im
2
=
2 . 475
2
= 1 . 75 A
Calcolo della massima tensione di polarizzazione
Trattandosi di tristori deve essere considerata la massima tensione di polarizzazione
diretta ed inversa sul componente
Per la configurazione di circuito considerata risulta:
Vidpk = Vpk = 2 ⋅ 220 = 311V
Diodi
Per quanto riguarda i diodi la condizione di funzionamento più gravosa è con α = π
In tali condizioni l’induttanza di filtro può essere carica al massimo valore di corrente
nel carico, corrente che deve “ricircolare” nei diodi D2+ e D2Si considera pertanto:
Corrente media nei diodi
Corrente efficace nei diodi
ID1+m = Im = 2.475 A
ID1+ = Im = 2.475 A
Fattore di forma della corrente nei diodi
Kf=1
Calcolo della tensione massima di polarizzazione
La massima tensione di polarizzazione inversa sul componente risulta:
Vipk = Vpk = 2 ⋅ 220 = 311V
Determinazione della potenza assorbita dalla rete per il caso in oggetto
Componente fondamentale della corrente di linea
Si consideri la forma d’onda della corrente assorbita dalla linea
17
α
Vpk
ωt
0
iT1+
Im
ωt
Im
iT1-
ωt
i1-
Im
ωt
Determinazione dell’armonica fondamentale della corrente di linea
Procedimento A
La corrente di linea non è una funzione pari o dispari , si determina pertanto:
2π
2π
π
1 1
1
T 1 + (ωt ) sin(ωt ) d (ωt ) + iT 1 − (ωt ) sin(ωt ) d (ωt ) =
I 1 A1 =
i
i
1(ωt ) sin(ωt ) d (ωt ) =
∫
2 π ∫0
2π ∫0
π
2π
2π
π
π
1
Im
sin(
)
(
)
sin(ωt )d (ωt ) =
Im
sin(
)
(
)
Im
sin(
)
(
)
t
d
t
t
d
t
t
d
t
ω
ω
−
ω
ω
=
ω
ω
−
∫
∫
∫
∫
2π α
2π α
π +α
π +α
Im
[− cos(ωt )]απ + [cos(ωt ]π2π+α = Im (1 + cos α + 1 − cos(π + α )) = Im [2 + cos α + cos α ] =
=
2π
2π
2π
2
Im[1 + cos α ]
=
2π
=
{
}
π
2π
2π
1 1
1
I 1B1 =
i
i
T 1 + (ωt ) cos(ωt )d (ωt ) + iT 1 − (ωt ) sin(ωt )d (ωt ) =
1(ωt ) cos(ωt )d (ωt ) =
∫
∫
∫
2π 0
2π 0
π
=
π
2π
2π
Im π
1
ω
ω
ω
ω
ω
ω
ω
ω
t
d
t
t
d
t
t
d
t
t
d
t
−
=
−
Im
cos(
)
(
)
Im
cos(
)
(
)
cos(
)
(
)
cos(
)
(
)
∫
=
∫
∫
∫
π
2π α
2
π +α
π +α
α
18
=
=
Im
2π
Im
2π
{[sin(ωt )]
π
α
}
− [sin(ωt ]π +α =
2π
[− sin α − sin α ] = −
2
2π
Im
2π
(sin π − sin α − sin 2π + sin(π + α )) =
Im sin α
_
I1A1
Diagramma vettoriale:
α/2
_
I1B1
_
Ve
α
Ampiezza della prima armonica di corrente:
I 1C1 = I 1A12 + I 1B12 =
2
2π
Im (1 + cosα ) 2 + sin2 α =
Procedimento B
2
2π
Im 2 + 2 cosα =
2
Im 1 + cosα
π
α/2
i1(ωt)
ωt
Si rende la funzione i1(ωt) dispari mediante traslazione dell’asse delle ordinate verso
destra di una quantità pari a α/2.
Si determina pertanto
I 1 A1 =
1 1
2 π
2π
∫ i1(ω t ) sin( ω t ) d (ω t ) =
0
=
2 Im
[− cos( ω t ) ]απ −/ α2 / 2 = 2 Im
2π
2π
=
α
4 Im
4 Im
cos
=
2
2π
2π
2
2π
π
∫ Im sin( ω t ) d (ω t ) =
0
2 Im
2π
α 2 Im
α
cos 2 − cos π − 2 =
2π
1 + cos α
2 Im
=
π
2
Diagramma vettoriale:
α/2
π −α / 2
sin( ω t ) d (ω t ) =
∫
α
/2
α
α
cos 2 + cos 2
1 + cos α
_
Ve
2
Im 1 + cos α
π
19
Procedimento C
i1
α
Im
ωt
i11
Im/2
ωt
i12
ωt
ωt
Si verifica come la corrente i1(ωt) è pari a :
i1(ωt) = i11(ωt) + i12(ωt)
con i11(ωt) ed i12(ωt) correnti con forma d’onda “quadra” e sfasate di α.
Si ricavano immediatamente le componenti fondamentali di i11 ed i12
4 Im
2 Im
sin(ωt ) =
sin(ωt )
π 2
π
2 Im
4 Im
i12(ωt ) → I 12C1 =
sin(ωt − α ) =
sin(ωt − α )
π 2
π
i11(ωt ) → I 11 A1 =
Diagramma vettoriale:
_
_
I11A1
_
I12C
Ve
α/2
_
α
I1A1
Potenza attiva assorbita dalla rete:
2
2
1 + cos α
α
α
=
P = Re(V e ⋅ I 1 A1*) = Ve ⋅ I 1 A1 cos = Ve ⋅ Im 1 + cos α ⋅ cos = VL ⋅ ⋅ Im 1 + cos α ⋅
π
π
2
2
2
=
1
2
2 Vpk
VL ⋅ (1 + cos α ) )Im =
(1 + cos α ) Im = Vpk ⋅ (1 + cos α ) Im = Vm Im = Pm = 200W
π
π
π
2
2
2 2
1 + cos α
α
α
α
⋅ sin =
Q = Im(V e ⋅ I 1 A1 *) = Ve ⋅ I 1 A1 ⋅ sin = Ve Im 1 + cos α ⋅ sin = Ve
Im
π
π
2
2
2
2
20
Vpk 1
2 2
α α Ve Im
α α Ve Im
Im⋅ cos sin =
2 ⋅ 2 cos sin =
2 ⋅ sin α =
Im 2 ⋅ sin α =
π
π
π
2 π
2 2
2 2
1
1
= Vm α =0 Im sin α = Pm α =0 sin α
2
2
= Ve
La corrente media nel carico con α = 73.9 e Vm = 126.5 V risulta:
Vm 126.5
=
= 1.58 A
80
R
220 ⋅ 1.58
2 sin 73.9 = 150.3Var
Q=
π
Im =
Potenza apparente assorbita dalla rete:
S = Ve ⋅ Im = 220 ⋅ 1.58 = 347.6VA
Potenza deformante assorbita dalla rete:
D = S 2 − P 2 − Q 2 = 347.6 2 − 200 2 − 150.3 2 = 241.3VA
21
Analisi del funzionamento
di un convertitore trifase a ponte non controllato
e del relativo trasformatore di alimentazione.
Lf
V’p1
N1
Il1
V’’12
N2
V’’1
Ip1
IS1
V’’2
Il2
D1+
D3+
V’’12
Vc
IS2
Vu
V’’23
Ip2
R
IS3
V’p2
V’23
Ip3
Il3
D2+
D1-
V’’2
D2-
D3-
V’p3
Linea di ingresso : linea di alimentazione trifase 380 V, 50 Hz
Carico: puramente resistivo
Dati nominali: Vnom = 350 V
Pnom = 20 kW
Ipotesi: diodi ideali
Induttanza di filtro Lf tale da potere ritenere la corrente nel carico priva di
armoniche.
Calcolo della tensione media al carico:
è opportuno definire preventivamente un diagramma vettoriale delle tensioni al
secondario del trasformatore.
V’’32
V’’31
V’’3
V’’12
V’’1
V’’21
V’’2
V’’13
V’’23
Da cui risulta la forma d’onda della tensione ai capi del carico.
22
V’’13 V’’32 V’’13 V’’13 V’’23 V’’21 V’’31 V’’32 V’’12 V’’13 V’’23 V’’21 V’’31
ωt
La tensione ai capi del carico è una tensione con periodo T/6 , detto T il periodo della
tensione di alimentazione del trasformatore, risulta pertanto una tensione con
frequenza pari a 50*6 = 300 Hz.
Il valore medio può essere calcolato isolando un intervallo di tempo pari a
20/6 ms = 3.33 ms.
1
Vm =
π /3
V’’12
=
π/3
π/6
2π/3
π/6
=
=
( 2 / 3 )π
∫V ''
12
pk ⋅ sin( ω t ) d (ω t ) =
π /3
2 ⋅ V ' '12
[− cos( ω t ) ]π( 2//33)π =
π /3
2 ⋅ V ' '12
2
π
cos − cos π =
3
3
π /3
2 ⋅V ' '12 3
=
π /3
π
2 ⋅ V ' '12
Oppure, in modo equivalente:
+π / 6
1
2 ⋅ V ' '12
Vm =
V ' '12 pk ⋅ cos(ωt )d (ωt ) =
[+ sin(ωt )]+−ππ // 66 = 2 ⋅ V ' '12 sin π + sin π =
∫
6
π / 3 −π / 6
π /3
π /3 6
=
3
2 ⋅ V ' '12
π
Avendo imposto una tensione media al carico pari a Vnom = 350 V, risulta che la
tensione secondaria del trasformatore dovrà essere:
V ' '12 =
π 1
π 1
Vm =
350 = 260 V
3 2
3 2
23
La corrente media assorbita del carico risulterà:
Im =
Pm 20000
=
= 57.14 A
Vm
350
Dimensionamento dei diodi del convertitore:
Corrente media in un diodo:
V’’12
ID1 + m =
ωt
Corrente efficace in un diodo:
ID1 =
Im
ωt
2π/3
Im
3
=
57.14
3
= 33 A
Fattore di forma della corrente in un
diodo:
KfID1 =
30°
Im 57.14
=
= 19.05 A
3
3
150°
Im 3
= 3 = 1.732
3 Im
Massima tensione di polarizzazione inversa dei diodi:
Vipk = V ' '12 pk = 2 ⋅ V ' '12 = 2 ⋅ 260 = 368V
Dimensionamento del trasformatore di alimentazione
Si considera il trasformatore come costituito da 3 avvolgimenti primari aventi
ciscuno N1 spire e 3 avvolgimenti secondari aventi ciascuno N2 spire.
Calcolo del rapporto spire del trasformatore:
V '1 N 1
V '12
=
=
V ' '1 N 2 V ' '12
= 3
3
V '12
V '12
N1
⇒
=
V ' '12
V ' '12
3 ⋅ N2
N1
380
= 3
= 2.531
N2
260
Potenza di dimensionamento di ciascun avvolgimento secondario del trasformatore:
A21 = V ' '1 ⋅ IS1
si determina pertanto la forma d’onda della corrente nel secondario del trasformatore
mediante la relazione:
iS1(ωt ) = iD1 + (ωt ) − iD1 − (ωt )
24
ωt
2π/3
iD1+(ωt)
Im
ωt
2π/3
iD1-(ωt)
Im
ωt
Im
ωt
2π
Valore efficace della corrente in ciascun avvolgimento secondario del tasformatore:
4 ⋅π
3
=
2π
IS1 = Im
2 ⋅ Im
3
=
2 ⋅ 57.14
3
= 46.65 A
Valore efficace della tensione ai capi di ciascun avvolgimento secondario del
trasformatore:
V ' '1 =
V ' '12
3
=
260
3
= 150.1V
Potenza di dimensionamento di un avvolgimento secondario:
A21 = V 1' '⋅IS1 = 46.65 ⋅ 150.1 = 7002VA
Potenza di dimensionamento del secondario:
A2 = 3 ⋅ A21 = 3 ⋅ 7002 = 21006VA
Mettendo in evidenza il rapporto tra la potenza di dimensionamento del secondario e
la potenza media al carico:
A2 = 3 ⋅ V ' '⋅IS = 3
V ' '12
3
Im
2
3
=3
2 π
1 π 1
= Vm ⋅ Im = 1.05 ⋅ Vm ⋅ Im = 1.05 ⋅ Pm = 20944VA
Vm ⋅ Im
3 3
3 3 2
25
Potenza di dimensionamento di un avvolgimento primario:
A11 = V '1 ⋅ Ip1 =
N1
N2
⋅ V ' '1 ⋅
IS1 = A21 = 7002VA
N2
N1
Potenza di dimensionamento del primario del trasformatore:
A1 = 3 ⋅ A11 = 3 ⋅ 7002 = 21006VA
Potenza di dimensionamento del trasformatore ( con riferimento alla potenza
assorbita del carico ).
A=
A1 + A2
π
= A1 = A2 = Pm = 20944VA
2
3
26
Determinazione della forma d’onda delle correnti di linea e di fase primarie:
ip1
N2
Im
N1
π
0
π/3
4π/3
5π/3
2π/3
2π
ωt
ip2
N2
Im
N1
ωt
ip3
N2
Im
N1
ωt
2
N2
Im
N1
Correnti di fase
primarie
i4=ip-ip3
N2
Im
N1
ωt
π/6
5π/6
Valore efficace dell’armonica fondamentale della corrente di fase primaria:
Ip1A1 =
2
π
∫i
2
(ωt ) ⋅ sin(ωt )d (ωt ) =
p1
0
=
5π / 6
N2
2 N2
5π / 6
Im⋅ sin(ωt )d (ωt ) =
Im[− cos(ωt )]π / 6 =
π N1
2π π / 6 N1
2
∫
2 N2 π
2 N2 3
3
6 N2
6 1
5π
=
+
=
Im cos − cos =
Im
Im
57.14 = 17.61
π N1
π 2.531
6
2 π N1
6 π N1 2
Il valore efficace dell’armonica fondamentale della corrente di linea primaria
risulterà:
Il1 A1 = 3Ip1 A1 = 17.61 ⋅ 3 = 30.49 A
27
Valore efficace della corrente di fase primaria:
Ip1 =
2
N1
=
Im
3
N2
2
1
57.14 = 18.43 A
3 2.531
Potenza attiva assorbita dalla rete
Con riferimento alle grandezze riportate in figura risulta:
V’1(ωt)
ip1(ωt)
ωt
ip1A1(ωt)
N1 1
6 N 2
N1
6 N2
Im =
P = 3 Re(V 1 ⋅ Ip1 A1 *) = 3 ⋅ V '1 ⋅ Ip1 A1 = 3 V ' '1 ⋅
Im = 3 ⋅
V ' '12
N2
π N1
N2 3
π N 1
N1 1 π
6 N 2
Vm
Im = Vm ⋅ Im = Pm = 20000W
= 3 ⋅
π
N
N
2
1
3
3
2
⋅
Potenza reattiva assorbita dalla rete:
Dall’analisi della figura si verifica che la potenza reattiva assorbita è nulla.
Potenza apparente assorbita dalla rete:
S = 3 ⋅ V 1 ⋅ Ip1 = 3 ⋅ 380 ⋅ 18.43 = 21010VA
Potenza deformante assorbita dalla rete:
D = S 2 − Pm 2 − Q 2 = 21010 2 − 20000 2 = 6436VA
28