ESAME di STATO 2009
Disegni a cura del prof. Cristiano DOMENICHELLI
Testi della prof.ssa Tiziana LA TORELLA
LICEO SCIENTIFICO “GALILEO FERRARIS”
1
ESAME DI STATO DI LICEO SCIENTIFICO
CORSO DI ORDINAMENTO
Sessione 2009
Indirizzo: SCIENTIFICO
Tema di: MATEMATICA
Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario.
PROBLEMA 1
È assegnato il settore circolare AOB di raggio r e ampiezza x ( r e x sono misurati, rispettivamente, in metri
e radianti).
1. Si provi che l’area S compresa fra l’arco e la corda AB è espressa ,
in funzione di x, da
S(x)
.
2. Si studi come varia S(x) e se ne disegni il grafico
(avendo posto
).
3. Si fissi l’area del settore AOB pari a 100m2 . Si trovi il valore di r
per il quale è minimo il perimetro di AOB e si esprima il corrispondente valore di x in gradi
sessagesimali (è sufficiente l’approssimazione al grado).
4. Sia
. Il settore AOB è la base di un solido W le cui sezioni ottenute con piani
ortogonali ad OB sono tutte quadrati. Si calcoli il volume di W.
Breve spiegazione :
Il problema presenta
un argomento di geometria (il calcolo dell’area del settore e del segmento circolare)
=
lo studio completo e il relativo grafico di una funzione trigonometrica
;
un problema di minimo
;
il volume del solido W con il calcolo di un integrale.
2
.
;
È assegnato il settore circolare AOB di raggio r e ampiezza x ( r e x sono misurati, rispettivamente,
in metri e radianti).
1. Si provi che l’area S compresa fra l’arco e la corda AB è espressa , in funzione di x,
da S(x)
.
Il segmento circolare ad una base è la parte del settore circolare compresa tra l’arco
3
e la corda AB.
La superficie
compresa tra l’arco
e il segmento AB si trova come differenza di aree:
:
Area del settore circolare
(
=
L’arco
)
=
si ottiene dalla proporzione
2
L’ area del triangolo
si calcola con la trigonometria
=
(Calcolo dell’area di un triangolo qualsiasi, noti due lati e l’angolo compreso)
=
punto 1)
4
2. Si studi come varia S(x) e se ne disegni il grafico (avendo posto
).
Studio della funzione S(x) :
1. Dominio :
2. Intersezioni con gli assi :
Asse x
I grafici delle funzioni
sono tangenti solo nell’origine O
3. Segno : y>o
4.
(dal grafico)
asintoti
5. Massimi e minimi :
:
La funzione è sempre crescente ,
6. Flessi :
7. Grafico :
punto 2)
5
3. Si fissi l’area del settore AOB pari a 100m2 . Si trovi il valore di r per il quale è minimo il
perimetro di AOB e si esprima il corrispondente valore di x in gradi sessagesimali
(è sufficiente l’approssimazione al grado).
Il problema di minimo si risolve definendo la costante : l’area del settore
=
= 100
Per determinare il perimetro del settore
Si devono trovare il lato OA = raggio r e l’arco
r =10
e
Si calcola il perimetro P
P=
+
+
.
x = 2 punto di minimo
x = angolo misurato in radianti
=
=
=115° punto 3)
Angolo misurato in gradi sessagesimali per il quale è minimo il perimetro del settore circolare
6
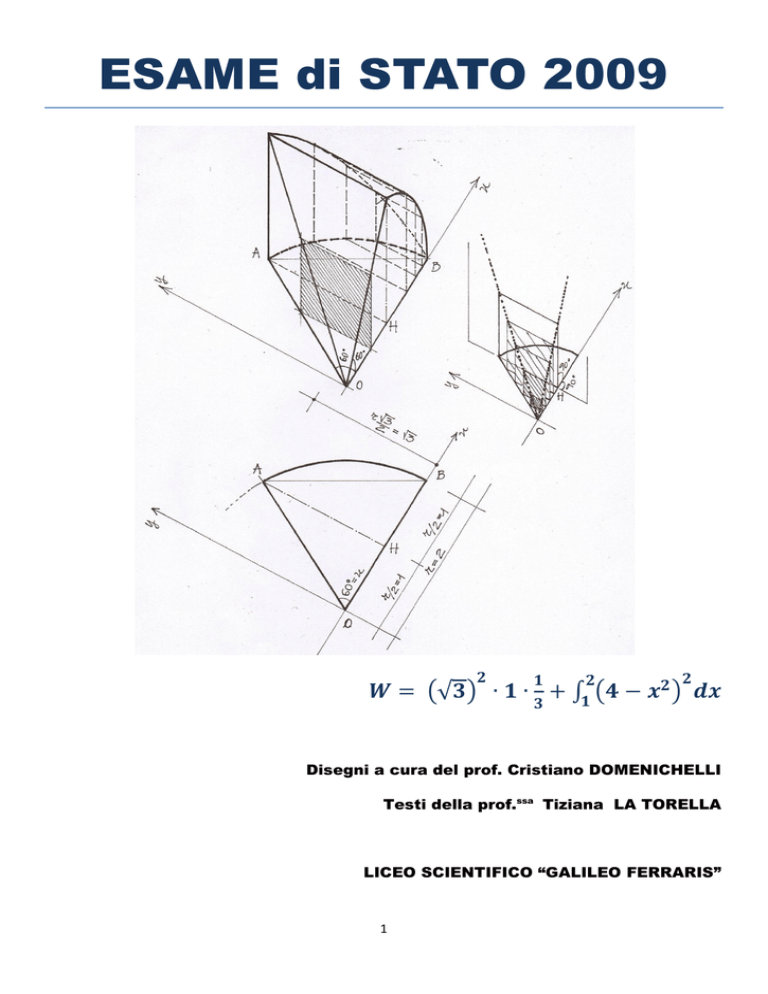
4. Sia
. Il settore AOB è la base di un solido W le cui sezioni ottenute con piani
ortogonali ad OB sono tutte quadrati. Si calcoli il volume di W.
W è la somma di due solidi : la piramide con base OAH e il solido con base HAB.
La piramide ha base quadrata
e altezza unitaria
punto4)
7
.
ESAME DI STATO 2009
disegni prof. Domenichelli
8











