Appunti preparati per il corso di Istituzioni di Fisica della Materia

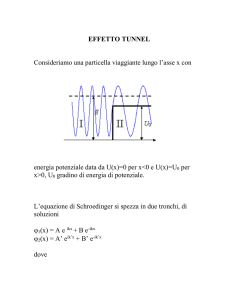
Appunti preparati per il corso di Istituzioni di Fisica della Materia corso di laurea in Scienza e
Ingegneria dei Materiali
Titolo del manoscritto: “Onde e quanti”
Copyright 2002 - Lorenzo Marrucci
Ultimo aggiornamento: 16 Maggio 2007
Capitolo 5 – Meccanica quantistica ondulatoria
In questo capitolo abbandoniamo il percorso storico-deduttivo del capitolo precedente e illustriamo
direttamente i principi fondamentali della meccanica quantistica, per come sono noti oggi. Prima di
iniziare, tuttavia, dobbiamo premettere che la meccanica quantistica in realtà ammette diverse
formulazioni fra loro equivalenti, anche se apparentemente molto diverse. Quella che presenteremo
in questo capitolo è denominata meccanica ondulatoria, perché si basa su una descrizione della
dinamica delle particelle in termini di onde associate o, come si usa dire oggi, funzioni d’onda. La
meccanica quantistica ondulatoria fu formulata per la prima volta in modo completo nel 1926 da
Erwin Schroedinger, che si basò sulle proposte iniziali di de Broglie. Poco prima, cioè nel 1925, era
stata invece formulata, dal giovanissimo Werner Heisenberg (che aveva solo 23 anni!), la cosiddetta
meccanica quantistica delle matrici, cui era pervenuto seguendo un percorso storico-scientifico
completamente indipendente da quello di de Broglie e Schroedinger. Entrambe le teorie
sembravano funzionare bene e questo inizialmente generò un certo sconcerto (dopo tanti anni in cui
non si riusciva a trovare una teoria fondamentale della fisica quantistica, improvvisamente ce ne
erano due!). Molto presto si provò che le due formulazioni erano matematicamente del tutto
equivalenti, come abbiamo anticipato. La meccanica delle matrici di Heisenberg era però molto più
astratta e di difficile utilizzo. Infatti, la consapevolezza diffusa che il mistero dei quanti, apertosi
con il lavoro di Planck e durato ben un quarto di secolo, era finalmente stato risolto si ebbe solo
dopo la pubblicazione dei lavori di Schroedinger.
5.1 Funzione d’onda di una particella con energia e quantità di moto definite
Per cominciare la nostra trattazione, riprendiamo per un momento il filo dello sviluppo storico
seguito nel capitolo precedente. Ricordiamo che l’idea base della proposta di de Broglie era che a
ad ogni particella, come ad esempio un elettrone o un fotone, deve essere associata un’onda. Tale
onda, come tutte le onde studiate finora, dovrà essere descritta matematicamente da una opportuna
funzione dello spazio e del tempo. Questa funzione è detta appunto funzione d’onda della particella,
ed è indicata di solito con il simbolo ψ (si legge “psi”). Nel caso unidimensionale, si avrà quindi la
funzione d’onda di una singola particella (caso 1D):
ψ(x,t)
(1.1)
In tre dimensioni, la variabile posizione x è sostituita dal vettore posizione r = (x, y, z) e si ha
funzione d’onda di una singola particella (caso 3D):
ψ(r,t) = ψ(x,y,z,t)
(1.2)
Per tutte le onde classiche che abbiamo studiato in precedenza, la funzione che descrive l’onda
corrisponde sempre ad una possibile dinamica di un campo, ossia una grandezza fisica definita
punto per punto e variabile nel tempo (come lo spostamento ξ dei pendoli). Per un fotone, la
funzione d’onda ψ presumibilmente descriverà le variazioni del campo elettrico o magnetico
1
dell’onda elettromagnetica associata. Ma nel caso di una particella materiale, come un elettrone,
non esiste invece alcun campo noto classicamente le cui variazioni siano descritte dalla funzione ψ.
Per dare un significato concreto alla (1.1) o (1.2), dobbiamo ipotizzare quindi l’esistenza di un
nuovo tipo di campo elettronico, analogo in qualche modo al campo elettromagnetico o al campo ξ
delle onde meccaniche, la cui dinamica è descritta dalla funzione ψ. Tuttavia, nell’ambito della
meccanica quantistica di singola particella non relativistica, si usa riferirsi alla ψ esclusivamente
con il termine funzione d’onda.
Secondo le relazioni di de Broglie, ad una data energia E della particella deve corrispondere una
ben precisa frequenza temporale ν = E/h dell’onda associata, e ad una data quantità di moto p della
particella deve corrispondere un ben preciso vettore d’onda k = p/ħ, e quindi una lunghezza d’onda
λ = 2π/|k|.
Ma la frequenza temporale e il vettore d’onda sono grandezze ben definite solo per le onde
armoniche piane. Onde che non siano armoniche non posseggono infatti una frequenza spaziale e
temporale unica e ben definita. Perciò, perché le relazioni di de Broglie abbiano un significato
preciso, è necessario che la funzione d’onda ψ corrispondente ad una particella di energia E e
quantità di moto p assegnate sia proprio un’onda armonica piana, ossia
funzione d’onda di particella con energia E e quantità di moto p:
(1.3)
ψ (r, t ) = Aei(k ⋅r −ωt ) = Aei(p⋅r − Et ) /
dove il significato e il valore della costante complessa A resta da definire. Se si sceglie l’asse x del
sistema di riferimento in modo che sia parallelo alla direzione di propagazione dell’onda, si ha
anche la seguente espressione 1D:
ψ (r, t ) = ψ ( x, t ) = Aei( kx −ωt ) = Aei( px − Et ) /
(1.4)
dove k = |k| e p = |p| denotano i moduli dei rispettivi vettori.
Come già discusso a proposito delle onde classiche, un’onda armonica piana ideale come quella
data dalle (1.3) o (1.4) è infinita nello spazio e nel tempo, ossia si estende su tutto lo spazio ed è
eterna. D’altra parte è chiaro che le onde armoniche piane sono sempre idealizzazioni, e che le onde
reali dovranno essere invece sempre finite, cioè saranno dei pacchetti d’onde, realizzabili come
sovrapposizioni di infinite onde armoniche (utilizzando l’integrale di Fourier). Ma un pacchetto
d’onde non ha una frequenza temporale e spaziale unica e ben definita, se non nel limite in cui
diventa infinitamente esteso. Questo sembra implicare, a sua volta, che una particella non possa
avere un’energia e una quantità di moto ben definite, se non come caso limite. In altre parole, nei
casi reali, in cui l’onda è finita, l’energia e la quantità di moto della particella non saranno
completamente definite, proprio come la frequenza temporale e spaziale di un’onda finita non sono
completamente definite. Il significato fisico preciso di questa “non definitezza” dell’energia e
quantità di moto della particella sarà chiarito più avanti.
Restringiamo ora la nostra trattazione al caso in cui la particella considerata sia una particella di
materia, cioè dotata di massa, come ad esempio un elettrone (ma non un fotone). Inoltre,
supponiamo per il momento che la particella sia libera nello spazio vuoto, ossia non soggetta a
forze esterne di alcun tipo. In questo caso, il legame tra l’energia E e la quantità di moto p è definito
dalla seguente espressione:
2
energia in funzione della quantità di moto per particella libera: E = 12 mv 2 =
p2
(1.5)
2m
Come abbiamo già notato nel capitolo precedente, utilizzando le relazioni di de Broglie questa
relazione si traduce nella seguente relazione di dispersione tra frequenza e vettore d’onda:
relazione di dispersione onde di particella libera:
k2
ω=
(1.6)
2m
E’ importante notare che questa relazione di dispersione è molto diversa da quella delle onde che
soddisfano l’equazione delle onde (equazione di D’Alembert) studiate finora. Infatti la frequenza
temporale ω dipende quadraticamente, anziché linearmente, dalla frequenza spaziale k. In
particolare, questo implica che la velocità non è la stessa per tutte le onde armoniche, ma dipende
dalla frequenza dell’onda. Infatti, utilizzando la derivazione della velocità di un’onda armonica del
paragrafo 2.2, si trova:
velocità di fase dell’onda associata alla particella libera: v f =
ω
k
=
k
(1.7)
2m
La velocità della particella libera di quantità di moto p = ħk è pari a v = p/m = ħk/m. Confrontandola
con la (1.7), notiamo il fatto strano che l’onda associata ad una particella libera viaggia ad una
velocità che è esattamente la metà di quella della particella! Questa stranezza è però legata alla
natura idealizzata dell’onda armonica, come vedremo più avanti, e si risolve non appena
consideriamo onde di estensione finita.
5.2 La particella libera in movimento: il pacchetto d’onde quantistico
Come già detto più volte, l’onda armonica è necessariamente un’idealizzazione, in quanto
infinitamente estesa. Per descrivere la dinamica di onde realistiche di estensione finita è quindi
necessario considerare dei pacchetti d’onde, o eventualmente impulsi o altre onde finite. Il
comportamento di tali pacchetti o altre onde finite può essere determinato a partire dalla relazione
di dispersione (1.6), mediante la rappresentazione dell’onda come integrale di Fourier (o
sovrapposizione) di infinite onde armoniche di diversa frequenza: 1
funzione d’onda finita (pacchetto d’onde) di particella libera: ψ ( x, t ) =
∞
∫ a ( k )e
ikx − iω ( k ) t
dk (2.1)
−∞
dove la funzione ω(k) da utilizzare è proprio quella data dall’equazione (1.6) e l’ampiezza a(k) delle
onde armoniche sovrapposte è anche data dalla trasformata di Fourier della funzione ψ(x) al tempo t
= 0, ossia
a(k ) =
1
2π
∞
∫ ψ ( x, 0)e
− ikx
dx
(2.2)
−∞
1
Questo paragrafo è scritto assumendo che il lettore non abbia studiato il contenuto del paragrafo 10 del secondo
capitolo, e quindi conterrà alcune ripetizioni dei concetti ivi introdotti.
3
Purtroppo, la (2.1) non ci consente facilmente di determinare la dinamica dell’onda in generale. In
particolare, non è più vero ciò che avevamo determinato con le onde classiche che soddisfano
l’equazione di D’Alembert, ossia che l’onda si muove senza cambiare di forma. La legge di
dispersione non lineare (1.6) cui obbediscono queste onde, che si traduce nel fatto che onde
armoniche di diversa frequenza hanno velocità (di fase) diverse come illustrato dalla (1.7), porta
invece alla conclusione che l’onda cambierà di forma mentre si propaga perché le diverse onde
armoniche si sfasano tra loro mentre viaggiano. Questo comportamento prende il nome di
dispersione.
E’ tuttavia possibile analizzare il movimento del pacchetto d’onde in modo approssimato nel caso
limite in cui questo sia ottenuto sovrapponendo solo onde armoniche appartenenti ad un piccolo
intervallo Δk centrato attorno ad una frequenza portante k0 (si veda il capitolo secondo, a proposito
dei pacchetti d’onde). Notate che, data la relazione ΔkΔx ≥ 1 discussa nel paragrafo 5 del capitolo
due, il caso considerato corrisponde anche al limite in cui il pacchetto d’onde è molto esteso nello
spazio (in rapporto alla lunghezza d’onda della portante, ossia deve presentare molte oscillazioni al
suo interno), ossia si avvicina al limite dell’onda armonica ideale.
In base alle assunzioni fatte, si ha quindi a(k) ≈ 0 al di fuori di un intervallo Δk centrato in k = k0,
per cui i valori di k molto diversi da k0 danno un contributo trascurabile all’integrale (2.1). Questo
fatto ci permette di sostituire l’argomento della funzione esponenziale all’interno dell’integrale (2.1)
con il suo sviluppo in serie di Taylor nella variabile k, centrato nel punto k = k0. In particolare è
necessario sviluppare la funzione ω(k) come segue:
ω ( k ) ≈ ω ( k0 ) +
dω
dk
( k − k 0 ) = ω 0 + v g ( k − k0 )
(2.3)
k = k0
dove abbiamo posto ω0 = ω(k0) e abbiamo introdotto la cosiddetta
vg =
velocità di gruppo:
dω
dk
=
k0
k0
m
(2.4).
Otteniamo così
ψ ( x, t ) ≈
∞
∫
a ( k )e
ikx − iω0t −i
dω
dk
k0
( k − k0 ) t
dk = e
(
)
− i ω0 − v g k0 t
−∞
∞
∫ a ( k )e
(
ik x − v g t
)
dk
(2.5)
−∞
Ora, al tempo iniziale t = 0, l’espressione della funzione d’onda è la seguente:
ψ ( x, 0) =
∞
∫ a ( k )e
ikx
dk
(2.6)
−∞
Confrontando l’integrale che appare nell’espressione (2.5) della ψ(x,t) con quello che appare nella
(2.6) per la ψ(x,0), otteniamo la seguente espressione approssimata per la dinamica del pacchetto
d’onde:
− i ω − v k )t
ψ ( x, t ) ≈ ψ ( x − v g t , 0) × e (
(2.7)
0
g 0
4
Questa espressione della funzione d’onda è di facile interpretazione. Se non ci fosse il fattore
esponenziale, la funzione ψ corrisponderebbe a quella di un’onda che non cambia forma avente una
velocità costante pari alla velocità di gruppo vg. Infatti, senza il fattore di fase la (2.7) è equivalente
alla (3.5) del capitolo secondo, con vg al posto di v0 e con la forma d’onda f(x) uguale all’onda
iniziale ψ(x,0). La presenza del fattore esponenziale modifica tuttavia la fase dell’onda in modo
variabile nel tempo. Per capire meglio la dinamica che ne risulta, separiamo esplicitamente onda
portante e inviluppo A(x) = |ψ(x)| della funzione d’onda iniziale come segue:
ψ ( x, 0) = A( x)eik x (2.8)
0
Inserendo questa espressione nella (2.7), otteniamo la seguente espressione:
dinamica approssimata di un pacchetto d’onde:
ψ ( x, t ) ≈ A( x − v g t )ei( k x −ω t )
0
0
(2.9)
Da questa, si vede che l’inviluppo A(x,t) si comporta esattamente come un’onda che non cambia
forma e che si muove uniformemente alla velocità di gruppo vg, mentre l’onda armonica portante si
muove alla sua velocità di fase v(k0)=ω0/k0, che in generale sarà diversa da vg.
Questa particolare dinamica è illustrata nella figura seguente. Osservando le tre istantanee della
figura, si può notare che mentre l’inviluppo dell’onda (in rosso) si muove ad una sua velocità
costante (quella di gruppo), le oscillazioni di campo associate all’onda portante (in blu, che
rappresenta la parte reale della ψ) si spostano all’interno dell’inviluppo ad una velocità diversa
(quella di fase), e quindi non si mantengano sincrone con l’inviluppo stesso.
inviluppo A(x)
ψ
t=0
t=1s
t=2s
x
Nel caso limite che stiamo considerando, dato che il pacchetto d’onde include solo frequenze
spaziali molto vicine a quella portante k0, la quantità di moto della particella è (almeno
approssimativamente) ben definita e vale p = ħk0, in base alle relazioni di de Broglie. Quindi, in
base alla (2.4) si ha p/m = vg, ossia la velocità di gruppo del pacchetto d’onde coincide proprio con
5
la velocità della particella. Perciò un’onda quantistica finita “viaggia insieme” alla particella, come
era ragionevole aspettarsi.
La dinamica descritta dalla (2.9) resta però pur sempre solo una prima approssimazione della
dinamica effettiva di un pacchetto d’onde. In particolare, un’analisi più attenta mostra che per tempi
sufficientemente lunghi anche l’inviluppo del pacchetto d’onde cambierà di forma in modo
significativo. Il tempo limite τ entro cui l’approssimazione (2.9) in cui l’inviluppo è costante è
ragionevolmente valida può essere stimato con il seguente ragionamento. Nell’integrale esatto (2.1),
la ω(k) compare moltiplicata per il tempo t, per cui il suo contributo viene amplificato nel tempo e
la precisione con cui bisogna valutare la ω all’interno dell’integrale cresce quindi nel tempo. Il
primo (e in questo caso unico) contributo trascurato nello sviluppo in serie di Taylor troncato (2.3) è
pari a δω = ħ(k−k0)2/(2m). Se Δk è la larghezza di banda dell’onda, questo termine contribuisce una
variazione di fase complessiva δϕ(t) ≈ ħΔk2t/(2m) nell’esponenziale immaginario che appare
nell’integrale (2.1) nell’intervallo di k in cui il coefficiente c(k) non si annulla. Finché δϕ << 1,
l’approssimazione (2.9) è valida. Ma quando, per t abbastanza grande, si ha δϕ(t) ≈ 1, il termine
considerato non può più essere trascurato e l’approssimazione cessa di valere. Quindi si ha:
limiti di validità approssimazione inviluppo costante: t
τ
2m
2mΔx 2
(2.10)
con τ =
≈
Δk 2
dove nella seconda espressione di τ abbiamo posto Δk ≈ 1/Δx. Per tempi confrontabili con τ o più
lunghi, le variazioni di forma dell’inviluppo del pacchetto d’onde diventano significative.
In alcuni casi particolari, è anche possibile svolgere l’integrale (2.1) analiticamente e determinare
così la dinamica esatta del pacchetto d’onde (comunque è sempre possibile eseguire l’integrale
numericamente con precisione arbitraria). Un esempio particolarmente importante è quello del
pacchetto d’onde gaussiano, ossia un’onda ψ data dalla seguente espressione iniziale (al tempo t =
0):
2
⎡
x − x0 ) ⎤
(
pacchetto d’onde gaussiano: ψ ( x, 0) = N exp ⎢ik0 x −
⎥ (2.11),
4σ 2 ⎦⎥
⎣⎢
dove N, k0, x0 e σ sono costanti reali (in realtà σ potrebbe anche essere presa complessa,
generalizzando ulteriormente la famiglia di onde considerate). In particolare, N è l’ampiezza
massima dell’inviluppo, k0 è la frequenza spaziale dell’onda portante, x0 è il centro del pacchetto
(nonché la posizione del massimo dell’inviluppo) e σ è una costante che fissa la larghezza
dell’inviluppo (purché sia reale).
Ora sostituendo la (2.11) nella (2.2) è possibile calcolare analiticamente l’ampiezza a(k) delle onde
armoniche componenti il pacchetto d’onde gaussiano (omettiamo i calcoli che sono analoghi a
quelli presentati nel capitolo secondo). Dopodiché, è possibile sostituire l’espressione di a(k) così
determinata nella (2.1) e svolgere analiticamente l’integrale in modo da trovare l’espressione
esplicita della ψ(x,t), ossia dell’onda per gli istanti di tempo successivi. Omettiamo i calcoli e
limitiamoci a riportare il risultato finale:
2
⎧
[
x − x0′ (t )] ⎫
dinamica del pacchetto gaussiano: ψ ( x, t ) = N ′(t ) exp⎨ik 0 x −
⎬
4σ′ 2 (t ) ⎭
⎩
(2.12)
6
dove sono state introdotte le seguenti tre funzioni del tempo:
k0
t
m
t
σ′(t ) = σ 2 + i
2m
x0′ (t ) = x0 +
N ′(t ) = N
(2.13)
⎛
k 02 ⎞
σ
⎜
exp⎜ − i
t ⎟⎟
σ′(t )
2
m
⎝
⎠
Notiamo che la (2.12) ha la stessa forma della (2.11) a patto di sostituire x0 con x′0(t), σ con σ′(t) e
N con N′(t) (notate però che ora σ′(t) e N′(t) sono complessi). In particolare, è interessante studiare
la dinamica dell’inviluppo dell’onda, che può essere calcolato rapidamente prendendo il moduloquadro della (2.12). Con un po’ di calcoli (attenzione al fatto che σ′ è una funzione complessa), si
trova il seguente risultato:
⎧⎪ [ x − x0′ (t ) ]2 ⎫⎪
A ( x, t ) = ψ ( x, t ) = N
exp ⎨ −
⎬
′′2
σ ′′(t )
⎩⎪ 2σ (t ) ⎭⎪
2
2
2
σ
(2.14)
dove abbiamo introdotto la nuova funzione σ′′(t), questa volta reale, definita come segue:
σ′′(t ) =
σ′(t )
σ
2
⎛ t ⎞
= σ 1+ ⎜
2 ⎟
⎝ 2mσ ⎠
2
(2.15)
La (2.14) è ancora una funzione gaussiana, centrata in x′0(t) e con larghezza σ′′(t).
Discutiamo prima la funzione x′0(t). Essa ci dice dove si trova e quindi come si sposta il centro del
pacchetto. Dalla prima delle (2.13), vediamo che il centro del pacchetto gaussiano compie un moto
rettilineo uniforme con velocità v = ħk0/m, ossia esattamente alla velocità di gruppo. Questo vale
senza limiti di tempo ed anche se il pacchetto non è particolarmente esteso nello spazio, ossia al di
fuori del limite di validità dell’approssimazione considerata prima.
Discutiamo ora l’andamento della larghezza σ′′(t) dell’inviluppo del pacchetto in funzione del
tempo. Per t = 0, essa coincide con quella iniziale σ. Per t > 0, invece, la (2.15) ci dice che la
larghezza cresce costantemente nel tempo. Perciò l’inviluppo dell’onda si “slarga”
progressivamente al trascorrere del tempo (questa è un’altra manifestazione del fatto che le onde
dispersive non sono di forma costante). Allo stesso tempo, in base alla (2.14), il massimo di
ampiezza dell’inviluppo si abbassa del fattore σ ′′(t ) .
Un esempio del movimento del modulo-quadro della funzione d’onda (o quadrato dell’inviluppo)
dato dalla (2.14) per un elettrone libero con velocità di gruppo vg = 2 nm/fs e con larghezza iniziale
del pacchetto σ = 1 Å = 0.1 nm, è dato nella seguente figura, contenente 5 istantanee successive,
intervallate di 1 fs = 10−15 s l’una dall’altra (con una larghezza σ così piccola, il tempo caratteristico
di cui alla (2.10) vale solo τ ≈ 0.2 fs, per cui già la seconda istantanea presa dopo 1 fs dalla prima
mostra forti cambiamenti nella forma dell’inviluppo). 2
2
Se volete vedere con i vostri occhi il movimento di un pacchetto d’onde, collegatevi al sito http://www.quantumphysics.polytechnique.fr/en/propa_wp.html. Potete scegliere di vedere sia la |ψ|2 che la parte reale Re(ψ) (quest’ultima
7
M ovim ento e s largam ento di un pacc hetto d'onde gaus siano relativo ad un elettrone
1.5
veloc ità di gruppo v = 2 nm /fs
larghezz a iniziale 0.1 nm
t= 0
|ψ |2
1
t= 1 fs
0.5
t= 2 fs
t = 3 fs
0
-20
0
20
40
x (A = 0.1 nm )
60
t = 4 fs
80
100
Ora, però, anziché continuare ad analizzare la dinamica di un pacchetto d’onde sulla base della sola
relazione di dispersione e dell’integrale di Fourier, è più fruttuoso cercare di determinare
l’equazione differenziale che governa le onde associate ad una particella materiale. Infatti, come
vedremo nel prossimo paragrafo, è solo per questa strada che si può estendere la nostra trattazione
al caso delle onde associate a particelle non libere, ossia soggette a forze esterne, come sono per
esempio gli elettroni all’interno degli atomi.
5.3 Equazione di Schroedinger dipendente dal tempo
L’equazione differenziale che governa le onde di materia ipotizzate da de Broglie fu determinata
per la prima volta da Erwin Schroedinger (si scrive anche così: “Schrödinger”), nel 1926, seguendo
un procedimento non molto diverso da quello che si descrive in questo paragrafo.
Restringiamo la nostra trattazione, per il momento, al caso unidimensionale in cui la funzione
d’onda ψ dipende solo dalla coordinata x e dal tempo t. Iniziamo inoltre dal caso di particella libera,
per il quale conosciamo già la relazione di dispersione, ossia la (1.6).
Per un’onda armonica come quella data dalla (1.4), valgono banalmente le seguenti semplici
relazioni sulle derivate parziali della ψ (sottolineo che queste relazioni valgono solo per le onde
armoniche):
∂
E
ψ = −iωψ = −i ψ
∂t
(3.1)
dà un’idea anche della dinamica della fase dell’onda), e in quest’ultimo caso potete notare come la velocità di fase (il
moto dei massimi delle oscillazioni) sia minore di quella di gruppo.
8
∂
p
ψ = ikψ = i ψ
∂x
⇒
∂2
p2
2
ψ
ψ
ψ (3.2)
=
−
k
=
−
2
∂x 2
Se ora prendiamo l’equazione (1.6), moltiplichiamo ambo i membri per ψ e utilizziamo le (3.1) e
(3.2) per sostituire ωψ e k2ψ con le rispettive derivate parziali, otteniamo la seguente equazione
differenziale:
i
∂ψ
∂ 2ψ
=−
2m ∂x 2
∂t
(3.3)
Per come l’abbiamo derivata, è chiaro che questa equazione differenziale sarà soddisfatta dalle onde
armoniche associate ad una particella libera. Trattandosi però di un’equazione lineare ed omogenea,
per essa vale il principio di sovrapposizione. Perciò, l’equazione sarà soddisfatta anche da una
qualsiasi sovrapposizione lineare di onde armoniche, ed anche da una sovrapposizione di infinite
onde armoniche, purché matematicamente ben definita. In altre parole, un qualsiasi pacchetto
d’onde dato dall’espressione (2.1) obbedirà ancora all’equazione (3.3), come è facile verificare
direttamente. Perciò, l’equazione differenziale (3.3) è proprio l’equazione delle onde associate alla
particella libera che cercavamo.
Tuttavia, ora vogliamo tentare di andare oltre il caso della particella libera e considerare il caso
generale e ben più importante della particella soggetta a forze esterne, cioè dobbiamo determinare
una sorta di “equivalente quantistico” dell’equazione F = ma di Newton.
Supponiamo ora che la forza esterna che agisce sulla particella sia una forza conservativa F(x),
funzione cioè solo della posizione della particella x e non ad esempio della sua velocità (questo
esclude ad esempio la forza magnetica). Perciò, possiamo introdurre un’appropriata energia
potenziale U(x), legata alla forza tramite la consueta relazione
F =−
dU
dx
(3.4)
Inoltre supponiamo per semplicità che tale energia potenziale sia anche costante nel tempo, ossia
che U sia funzione solo di x e non della variabile temporale t.
Per cominciare la nostra ricerca dell’equazione differenziale delle onde di materia, notiamo
innanzitutto che le relazioni di de Broglie dovrebbero conservare, anche nel caso in cui la particella
è soggetta a forze esterne, una qualche validità, almeno approssimata. Infatti, de Broglie le utilizzò
per dare una spiegazione al postulato di Bohr sull’elettrone nell’atomo di idrogeno, cioè in presenza
di una forza esterna (cioè l’attrazione coulombiana del nucleo).
Proviamo quindi a seguire una strada simile a quella seguita con la particella libera. Iniziamo dalla
relazione tra l’energia totale E della particella e la sua quantità di moto p, che nel caso di particella
soggetta a forza esterna è data dalla seguente espressione:
energia di particella soggetta a forza conservativa (in funzione di p e x):
p2
E=
+ U ( x)
2m
(3.5)
dove il primo termine è l’energia cinetica scritta in funzione della quantità di moto, come nella (1.5).
9
Consideriamo ora per prima cosa il caso limite in cui l’energia potenziale U(x) varia molto
lentamente nello spazio, tanto da poterla considerare come se fosse approssimativamente costante
(questo corrisponde ad una forza esterna molto debole), ma non nulla. Da un punto di vista classico
la particella si comporta esattamente come se fosse libera, perché una costante additiva nell’energia
potenziale corrisponde ad una forza nulla e non influenza il moto. Ma ripercorrendo i passaggi già
seguiti nel paragrafo precedente con la (3.5) al posto della (1.5), otteniamo la seguente relazione di
dispersione:
ω=
k2
+U
2m
2
(3.6)
Notiamo che questa equazione, da un punto di vista ondulatorio, non è affatto equivalente alla
relazione (1.6) trovata in precedenza. Moltiplicando ora ambo i membri di questa equazione per ψ e,
utilizzando le (3.1) e (3.3), otteniamo la seguente equazione differenziale:
i
2
∂ψ
∂ 2ψ
=−
+ Uψ
2m ∂x 2
∂t
(3.7)
Questa equazione, derivata dalle relazioni di de Broglie, per come è stata derivata dovrebbe essere
valida in modo esatto solo nel limite in cui U(x) è perfettamente costante. L’ipotesi avanzata da
Schroedinger fu che l’equazione (3.7) valga invece in modo esatto sempre, cioè senza nessuna
approssimazione, anche nel caso generale in cui U(x) non è affatto costante. Notiamo che non c’è
nessun modo di dimostrare questo risultato a partire dalle relazioni di de Broglie o da altri principi
precedentemente assunti, per cui esso può essere considerato come un vero e proprio postulato della
nuova meccanica quantistica che stiamo costruendo, una legge che determina la dinamica delle
onde di materia associate a particelle soggette a forze esterne, e che quindi svolge un ruolo del tutto
analogo a quello della seconda legge di Newton F = ma nella meccanica classica. La validità
dell’ipotesi di Schroedinger poteva essere dimostrata, come poi effettivamente avvenne, solo dal
confronto delle previsioni che scaturiscono dall’equazione (3.7) nel caso generale con i risultati
degli esperimenti.
Abbiamo quindi determinato la seguente legge generale che governa la dinamica delle onde di
materia:
equazione di Schroedinger dipendente dal tempo (caso 1D):
2
∂ψ
∂ 2ψ
i
=−
+ U ( x)ψ
2m ∂x 2
∂t
(3.8)
Come riportato sopra, questa equazione ha preso il nome del suo scopritore. La dizione “dipendente
dal tempo” è usata per distinguere questa equazione da un’altra equazione che vedremo più avanti,
sempre dovuta a Schroedinger e a lui intitolata, ma in cui il tempo non appare. Vediamo ora alcune
importanti proprietà dell’equazione (3.8).
1) Come le equazioni precedentemente studiate, anche l’equazione di Schroedinger (3.8) è lineare
ed omogenea e quindi le sue soluzioni soddisfano il principio di sovrapposizione. Inoltre, se
ψ(x,t) è una soluzione qualsiasi della (3.8), allora anche la funzione ψ′ = c ψ(x,t), dove c è una
costante complessa qualsiasi, sarà soluzione della (3.8).
2) Nel caso generale in cui l’energia potenziale U(x) non è costante, l’equazione (3.8), al contrario
di quelle viste in precedenza, non è un’equazione a coefficienti costanti. Questo fa sì che le
10
semplici funzioni esponenziali non siano soluzioni valide. In particolare, le onde armoniche
non sono soluzioni della (3.8) nel caso generale in cui U(x) non è costante.
3) L’equazione di Schroedinger (3.8) è un’equazione differenziale alle derivate parziali del primo
ordine nel tempo (e del secondo ordine nella coordinata x). In questo essa differisce
dall’equazione di D’Alembert, che è del secondo ordine nel tempo. Che cosa comporta questa
differenza di ordine rispetto all’equazione di D’Alembert? In effetti c’è una importante
differenza, che può essere derivata da un teorema matematico sull’esistenza e unicità delle
soluzioni delle equazioni differenziali: le soluzioni della (3.8) sono fissate univocamente
assegnando come condizioni iniziali la sola funzione d’onda ψ(x) al tempo iniziale (ad esempio
t = 0). Non è invece necessario conoscere anche la derivata ∂ψ/∂t al tempo iniziale (infatti
questa derivata risulta fissata dall’equazione (3.8)). 3 Questo fatto fa sì che la funzione ψ(x)
assegnata per tutti i valori di x per un t fissato, ossia l’“istantanea” dell’onda ψ, costituisca tutta
l’informazione necessaria e sufficiente a definire univocamente l’evoluzione successiva
dell’onda ψ(x,t). Per questo motivo, questa funzione d’onda ψ(x) con t fissato, solitamente
indicata con il medesimo simbolo ψ della funzione completa ψ(x,t), definisce il cosiddetto stato
quantistico della particella all’istante t.
4) Infine, l’equazione di Schroedinger (3.8) è un’equazione a coefficienti complessi, ossia in cui
compare esplicitamente l’unità immaginaria i. Questo implica, a sua volta, che la funzione ψ
deve essere necessariamente una funzione complessa, in quanto non esistono soluzioni reali
della (3.8). Anche se proviamo a partire all’istante t = 0 con una funzione ψ(x) tutta reale, la
soluzione ψ(x,t) sarà complessa per t > 0. Ne concludiamo che la notazione complessa, nel
caso delle onde di materia della meccanica quantistica, non è più un artificio di calcolo, ma
una necessità. In altre parole, al contrario del caso delle onde classiche, nelle onde di materia
l’informazione sulla situazione fisica reale non è più contenuta nella sola parte reale della ψ,
bensì in entrambe le parti reale ed immaginaria.
Un modo compatto per riscrivere l’equazione (3.8) si basa sulla preliminare definizione del
seguente
operatore differenziale hamiltoniano (particella singola 1D):
Hˆ = −
∂2
+ U ( x)
2m ∂x 2
2
(3.9)
Una volta introdotto questo operatore, l’equazione (3.8) si può riscrivere come segue:
equazione di Schroedinger dipendente dal tempo (forma astratta): i
∂ψ
= Hˆ ψ
∂t
(3.10)
Tale notazione formale può apparire inutile, perché per affrontare l’equazione dobbiamo comunque
esplicitare l’operatore hamiltoniano con la (3.9), tornando così alla (3.8). Ma la sua utilità deriva dal
fatto che, al contrario della (3.8), l’equazione (3.10) è generalizzabile a sistemi fisici più complessi
di quello considerato, cioè la particella singola soggetta ad una forza esterna conservativa. Infatti, la
(3.10) ha validità del tutto generale in meccanica quantistica. Quello che cambia da un sistema
fisico all’altro è l’espressione esplicita dell’operatore hamiltoniano e le variabili da cui dipenderà la
funzione d’onda ψ.
Nel caso delle soluzioni dell’equazione di D’Alembert, ricordiamo che era necessario fissare il valore in tutti i punti x
della funzione incognita ξ e della sua derivata rispetto al tempo ∂ξ/∂t, ossia, nell’esempio della catena dei pendoli, la
posizione e la velocità iniziale di tutti i pendoli.
3
11
Inoltre, l’utilità della (3.10) è anche data dal fatto che esiste una procedura generale per
determinare l’operatore hamiltoniano Ĥ di un sistema fisico. Rimandiamo tuttavia ad un capitolo
successivo la descrizione di questa procedura, che al momento risulterebbe di difficile
comprensione.
Una prima generalizzazione dell’equazione (3.8) è il passaggio dal caso unidimensionale al caso
tridimensionale in cui il potenziale U che definisce la forza esterna e la funzione d’onda ψ della
particella possono dipendere da tutte e tre le coordinate spaziali x, y e z. Questa generalizzazione è
abbastanza semplice e la possiamo ottenere in due modi equivalenti: o ripercorrendo i passaggi
mostrati per il caso 1D, oppure considerando l’unica generalizzazione possibile della (3.8) che
rispetti i requisiti di simmetria dello spazio. Il risultato finale è comunque, come nel caso
dell’equazione delle onde, quello di sostituire la derivata seconda rispetto a x con l’operatore
laplaciano ∇2, ossia:
equazione di Schroedinger dipendente dal tempo (3D):
2
∂ψ
i
=−
∇ 2ψ + U (r )ψ
2m
∂t
(3.11)
Analogamente viene cambiata l’espressione dell’operatore hamiltoniano rispetto a quella 1D. Tutte
le proprietà della (3.11) sono ovvie generalizzazioni delle proprietà della (3.8). In particolare, lo
stato quantistico ad un istante di tempo t fissato è definito in 3D dalla funzione ψ(r).
In conclusione, abbiamo determinato l’equazione differenziale che governa la dinamica delle onde
di materia associate alle particelle dotate di massa, come l’elettrone. Resta ancora aperto, però, il
problema di capire quale sia il significato fisico reale di queste onde. Questo sarà l’argomento del
prossimo paragrafo.
5.4 Interpretazione probabilistica della funzione d’onda
Ricapitoliamo brevemente quello che abbiamo definito finora su questa nuova meccanica
quantistica. Abbiamo stabilito, con De Broglie, che ad ogni particella materiale va associata
un’onda. Se l’onda è armonica piana, allora le relazioni di de Broglie fissano il legame tra energia
della particella e frequenza dell’onda associata, nonché tra quantità di moto della particella e vettore
d’onda dell’onda associata. Più in generale, con l’equazione di Schroedinger, abbiamo stabilito
come si propaga l’onda associata ad una particella, anche in presenza di forze esterne.
Tuttavia, resta ancora sostanzialmente indefinita la vera natura del legame tra la particella e la sua
onda associata. Innanzitutto, se l’onda non è armonica piana non sappiamo bene come applicare le
relazioni di de Broglie, perché frequenza e vettore d’onda non sono più definiti univocamente. Su
questo punto torneremo in un paragrafo successivo. Ma soprattutto una particella, prima ancora che
da un’energia e una quantità di moto, è caratterizzata ad ogni istante di tempo da una ben precisa
posizione nello spazio. Invece l’onda è sempre distribuita su una regione più o meno ampia di
spazio. Che legame c’è, dunque, tra l’onda associata ad una particella e la posizione della particella
stessa?
Dopo il lavoro di Schroedinger, c’era chi proponeva che le particelle come oggetti puntiformi
caratterizzati da una posizione ben precisa non esistessero affatto, e che l’unica cosa realmente
esistente fossero le onde associate (fra questi c’era lo stesso Schroedinger). Forse gli elettroni erano
solo onde, dopotutto? L’apparenza “particellare” potrebbe essere forse solo il risultato di una
parziale localizzazione dell’onda, ossia della formazione di un pacchetto d’onde di estensione
12
sufficientemente piccola. Ma questa interpretazione “classica” della meccanica quantistica si
trovava in conflitto con diverse evidenze sperimentali, come già lo stesso effetto fotoelettrico nel
caso dei fotoni, nonché i primi esperimenti di diffusione (in inglese, scattering) di particelle
materiali. In questi ultimi, ad esempio, risolvendo l’equazione di Schroedinger si ottiene sempre
un’onda sferica che si allarga progressivamente dal centro diffusore. Tuttavia, sperimentalmente, le
particelle diffuse vengono sempre trovate in un punto preciso, e non sono mai “spalmate” in tutta la
superficie sferica dell’onda. In altre parole, le particelle mostrano di avere sempre una posizione
ben precisa, quando viene misurata, e risultano localizzate in una regione molto più piccola
dell’estensione dell’onda associata. Tale posizione misurata della particella, tuttavia, sembra
variare in modo casuale e incontrollabile da una prova alla successiva.
Un esperimento, in particolare, indica con chiarezza quale sia la reale relazione tra l’onda e la
posizione della particella. Si tratta del famoso esperimento di interferenza di Young delle due
fenditure. Se questo esperimento viene compiuto con la luce in condizioni normali di intensità, sullo
schermo posto di fronte alle fenditure si vedranno anche ad occhio nudo le frange luminose dovute
all’interferenza delle onde provenienti dalle due fenditure. Le frange, come è noto, sono rapide
oscillazioni spaziali dell’intensità luminosa, ossia dell’ampiezza delle onde elettromagnetiche sullo
schermo. 4
Ma dove sono finiti i fotoni in questo esperimento di interferenza? In realtà i fotoni sono sempre lì,
solo che in condizioni normali di intensità non li distinguiamo perché sono troppo numerosi. Con
un semplice calcolo è facile verificare che una lampadina da 100 W emette circa 1020 fotoni al
secondo (se la loro frequenza è nel visibile)! Quindi si capisce bene che su ogni porzione, anche
minuscola, dello schermo, anche in un intervallo piccolissimo di tempo arrivano sempre diversi
miliardi di fotoni. E’ quindi impossibile distinguerli, e l’unica cosa che si può percepire (a occhio
nudo, ma anche con i migliori rivelatori di luce) è il loro effetto cumulativo, che ci appare sotto
forma di una illuminazione apparentemente continua nel tempo, con delle modulazioni continue
nello spazio, ossia le frange d’interferenza.
Se però ora eseguiamo l’esperimento dopo aver abbassato moltissimo l’intensità luminosa, in modo
che ci siano solo pochi fotoni o, al limite, solo un fotone alla volta (in media) che viaggia dentro
l’apparato, saremo in grado di rivelare il suo arrivo sullo schermo in modo distinto, purché il
rivelatore sia abbastanza sensibile. Rivelatori capaci di “vedere” un singolo fotone di luce esistono.
Possiamo immaginare quindi che lo schermo contenga tanti piccoli rivelatori (oppure una pellicola
fotografica estremamente sensibile). Cosa osserveremo allora? Troveremo lo schermo viene colpito
da ogni fotone sempre in un solo punto preciso, proprio come ci si aspetterebbe per l’arrivo di una
particella puntiforme. Via via che arrivano altri fotoni, il punto dello schermo che viene colpito
cambia ogni volta, apparentemente a caso. Registrando in modo cumulativo (ad esempio con una
fotografia a lunga esposizione) tutti gli arrivi successivi dei fotoni, troveremo che essi si
accumulano proprio nelle regioni dello schermo dove, ad alte intensità, apparivano le frange chiare
di interferenza, mentre i fotoni non colpiscono mai o quasi mai le zone dove c’erano le frange scure.
Eseguendo una statistica sulla distribuzione casuale del punto di arrivo dei fotoni, cioè
rappresentando il numero di fotoni arrivati in ciascuna piccola area dello schermo in funzione della
posizione, si ottiene una figura identica alle frange d’intensità luminosa osservate ad alta intensità.
Si può eseguire esattamente lo stesso esperimento di interferenza da due fenditure con un fascio di
elettroni al posto della luce (è solo molto più complesso da realizzare tecnicamente, ma è stato fatto,
la prima volta nel 1961). A parità di lunghezza d’onda (fissata dalla quantità di moto iniziale degli
4
Potete eseguire “virtualmente” questo esperimento d’interferenza con il computer, collegandovi al sito
http://www.mi.infn.it/~phys2000/schroedinger/two-slit2.html. E’ possibile anche variare la distanza tra le fenditure e
modificare così la figura d’interferenza.
13
elettroni), le frange di interferenza sono essenzialmente identiche a quelle luminose. Eseguendo
l’esperimento con pochi elettroni alla volta, troviamo ancora che essi colpiscono lo schermo a caso.
Eseguendo una statistica sul punto di impatto di molti elettroni si ottengono nuovamente le frange
di interferenza. 5
Analizzando esperimenti come quelli discussi, il fisico tedesco Max Born concepì, nel 1927, la
cosiddetta interpretazione probabilistica (o statistica) della funzione d’onda, che oggi rappresenta
uno dei principi fondamentali della meccanica quantistica. Per semplicità, iniziamo dal caso 1D.
Supponiamo di avere una particella la cui funzione d’onda sia ψ(x,t). Se ad un certo istante di tempo
t eseguiamo una misura della posizione x occupata dalla particella, il risultato della misura sarà
casuale. In altre parole, ripetendo più volte l’esperimento, troveremo ogni volta la particella in una
posizione diversa, a caso, anche se la funzione d’onda ψ(x,t) prima della misura è sempre la stessa.
Tuttavia, la casualità nella posizione misurata della particella non è completa. Infatti, ripetendo
molte volte l’esperimento, la particella sarà trovata più frequentemente nell’intorno dei punti in cui
l’onda ψ ha un’ampiezza maggiore, più raramente dove l’ampiezza è minore, e mai dove l’onda ψ
si annulla. Più precisamente, la posizione misurata della particella è una variabile casuale che
obbedisce alla seguente legge probabilistica: 6
probabilità che la particella sia localizzata in un intervallo spaziale infinitesimo Δx centrato in x:
2
ΔP( x) ∝ ψ ( x) Δx (4.1)
dove il simbolo ∝ indica una relazione di proporzionalità diretta e qui, così come nelle restanti
equazioni di questo paragrafo, la dipendenza dal tempo è sottintesa.
Il rapporto ΔP/Δx, nel limite in cui Δx → 0, diventa indipendente dall’intervallo stesso e definisce
punto per punto la probabilità per unità di lunghezza, ossia la cosiddetta
densità (o distribuzione) di probabilità (caso 1D):
dP
ΔP( x)
( x) = lim
Δ
x
→
0
dx
Δx
(4.2)
In base alla (4.1), dunque, la densità di probabilità per la posizione della particella è proporzionale
al modulo-quadro della funzione d’onda, ossia
densità di probabilità per la posizione della particella (caso 1D):
dP
2
( x) ∝ ψ ( x) (4.3)
dx
Ora, come vedremo più avanti, la funzione d’onda ψ di una singola particella materiale è
determinata completamente dalla situazione fisica salvo per una costante moltiplicativa, che può
essere scelta del tutto arbitrariamente. In altre parole, se ψ′(x,t) è la funzione d’onda associata ad
una particella in un dato sistema fisico, anche la funzione ψ′′(x,t) = c ψ′(x,t) può essere usata per
descrivere la medesima particella. La costante moltiplicativa c può essere in particolare sempre
scelta in modo da ottenere una funzione d’onda ψ′′ per la quale la relazione di proporzionalità della
legge (4.1) si trasforma in una eguaglianza. In questo caso si dice che la funzione d’onda ψ è stata
5
Al sito http://www.mi.infn.it/~phys2000/schroedinger/two-slit3.html potete eseguire “virtualmente” l’esperimento di
interferenza con gli elettroni.
6
Ricordiamo che la probabilità P di un evento casuale è legata alla frequenza f con cui questo si verifica in una serie di
N prove ripetute dalla seguente legge: P = lim N →∞ f N . Anche questo limite va però inteso in senso probabilistico,
ossia la probabilità di ottenere uno scarto tra P e f/N maggiore di un valore assegnato, pur piccolo a piacere, tende a zero
al divergere di N.
14
normalizzata. In altre parole, possiamo sempre scegliere la nostra funzione d’onda ψ in modo che
valga la seguente legge:
densità di probabilità per la posizione della particella (ψ normalizzata, 1D):
dP
2
( x) = ψ ( x) (4.4)
dx
In questa espressione la dipendenza dal tempo è stata sottintesa. In generale, cioè, questa densità di
probabilità sarà funzione del tempo. Un primo esempio di tale dipendenza è la dinamica del
modulo-quadro del pacchetto d’onde gaussiano descritta nel secondo paragrafo. Si nota, in
particolare, come la curva della densità di probabilità si allarga progressivamente nel tempo,
rendendo la posizione della particella sempre più incerta.
Fermiamoci ora un attimo, per notare una importante differenza che abbiamo individuato tra le onde
quantistiche e le onde classiche. Il modulo quadro dell’onda nel caso delle onde classiche è
proporzionale alla densità di energia, oppure (con una diversa costante di proporzionalità)
all’intensità dell’onda. Nelle onde quantistiche, invece, il modulo quadro dell’onda non ha alcuna
relazione con l’energia del sistema (che invece come sappiamo è legato alla frequenza temporale
dell’onda, se questa è armonica), ma fissa invece la distribuzione di probabilità per le posizioni
della particella. Per questo motivo le onde quantistiche sono a volte denominate onde di probabilità.
Una volta assegnata la densità di probabilità, è possibile da questa calcolare la probabilità che la
particella sia localizzata in un qualsiasi intervallo spaziale (x1, x2):
x2
probabilità che la particella sia localizzata tra x1 e x2: P( x1 < x < x2 ) = ∫ ψ ( x) dx (4.5)
2
x1
In particolare, la probabilità che la particella si trovi in un punto qualsiasi di tutto lo spazio deve
corrispondere alla certezza, ossia deve avere valore unitario. Questa corrisponde alla cosiddetta
∞
condizione di normalizzazione (caso 1D):
∫ ψ ( x)
2
dx = 1 (4.6)
−∞
Questa condizione di normalizzazione è proprio il requisito perché si possa usare la (4.4) anziché la
meno completa (4.3). In un certo senso, la condizione di normalizzazione restringe l’insieme di
funzioni d’onda fisicamente ammissibili. Essa viene usata per fissare il modulo della costante
moltiplicativa che appare a fattore dell’intera funzione d’onda, ossia per fissare l’ampiezza
complessiva dell’onda. In altre parole, se abbiamo già determinato una funzione d’onda non
normalizzata ψ′ del sistema, si può sempre passare ad una funzione normalizzata ψ′′ mediante la
posizione ψ′′ = c ψ′, dove il modulo |c| del coefficiente c viene fissato imponendo la validità della
(4.6) per la ψ′′ (è facile verificare che c = 1
∫
+∞
−∞
ψ ′ dx ). 7 La condizione per poter ottenere una
2
funzione d’onda normalizzata con questo metodo è però che la ψ′ sia già normalizzabile, ossia che
l’integrale
∫
+∞
−∞
ψ ′ dx esista e sia finito. Come discuteremo più avanti, non tutte le funzioni
2
Un tipico caso in cui si ottiene una funzione d’onda non normalizzata è quello dell’applicazione del principio di
sovrapposizione: se ψ1 e ψ2 sono due funzioni d’onda già note, normalizzate e soluzioni dell’equazione di
Schroedinger, la loro somma ψ′ = ψ1+ψ2 è ancora soluzione dell’equazione di Schroedinger, ma in generale non sarà
più normalizzata. Quindi sarà di solito necessario introdurre un opportuno fattore di normalizzazione c e definire la
nuova soluzione come ψ = c ψ′ = c (ψ1+ψ2).
7
15
soddisfano a questo requisito. Quelle che non lo soddisfano non sono fisicamente ammissibili, se
non come caso limite (rientrano in questa categoria, ad esempio, le onde armoniche).
Resta invece del tutto indeterminato il fattore di fase c/|c| = eiα dove la fase è α = arg(c). In effetti,
la fase complessiva della funzione d’onda non ha significato fisico, cioè non ha nessuna
conseguenza misurabile, per cui può essere scelta in modo del tutto arbitrario. Invece ha un
significato fisico ben preciso la differenza di fase della funzione d’onda tra punti diversi dello
spazio o tra istanti di tempo diversi.
Un dubbio importante potrebbe ora assalire un lettore particolarmente attento. Supponiamo che al
tempo t = 0 si abbia una funzione d’onda ψ(x,0) che soddisfa la condizione di normalizzazione
(4.6). Per tempi successivi, la funzione ψ(x,t) sarà interamente determinata dall’equazione di
Schroedinger (3.8), per cui per t > 0 non siamo più liberi di scegliere la costante moltiplicativa c da
usare per normalizzare. Chi ci garantisce allora che la condizione di normalizzazione (4.6)
continuerà a valere? La risposta è che l’equazione di Schroedinger mantiene automaticamente
valida la condizione di normalizzazione per t > 0 se questa è valida inizialmente per t = 0. Questo
può essere dimostrato matematicamente (la dimostrazione è omessa) ed è un’importante conferma
della correttezza dell’equazione di Schroedinger. Ad esempio, abbiamo visto in precedenza che il
pacchetto d’onde gaussiano associato alla particella libera si abbassa di ampiezza mentre si slarga.
Non è difficile verificare che le due variazioni si compensano in modo tale da mantenere costante
l’integrale del modulo quadro della funzione d’onda.
Vediamo ora l’equivalente tridimensionale (3D) delle relazioni (4.4)-(4.6). In tre dimensioni, si
definisce la seguente probabilità per unità di volume (anziché di lunghezza):
densità di probabilità per la posizione della particella (3D):
dP
2
(r ) = ψ (r ) (4.7)
dV
(anche qui, se la funzione d’onda ψ non è normalizzata, il segno di uguale va sostituito con un
segno di proporzionalità). La probabilità che la particella sia localizzata in una qualsiasi regione
finita di spazio Ω è data dal seguente integrale (triplo) di volume:
probabilità che la particella sia nel volume Ω: P (r ∈ Ω) = ∫ ψ (r ) dV = ∫∫∫ ψ ( x, y, z ) dxdydz (4.8)
2
2
Ω
Ω
La condizione di normalizzazione è infine la seguente:
condizione di normalizzazione (caso 3D):
∫ ψ (r)
Ω∞
∞ ∞ ∞
2
dV =
∫ ∫ ∫ ψ ( x, y , z )
2
dxdydz = 1 (4.9)
−∞ −∞ −∞
Come si è detto in precedenza, quando viene eseguito un esperimento che consente di misurare la
posizione di una particella, questa viene sempre localizzata in una posizione ben precisa, proprio
come in meccanica classica. Tale posizione non è tuttavia prevedibile in modo certo conoscendo la
funzione d’onda: sono possibili solo previsioni probabilistiche. Si potrebbe pensare che questo
carattere probabilistico sia dovuto semplicemente al fatto che la funzione d’onda è in realtà una
descrizione incompleta della situazione fisica, cioè che non fornisce tutte le informazioni su un
certo sistema fisico (ad esempio una particella).8 Se questo fosse vero, basterebbe forse aggiungere
8
Questo è ad esempio ciò che pensava Einstein, che non accettò mai, in termini puramente filosofici, la formulazione
definitiva della meccanica quantistica. Famosa, a tal riguardo, è la sua frase “Dio non gioca a dadi”.
16
la conoscenza di ciò che manca per poter tornare a prevedere tutto in modo deterministico (ossia
con certezza, senza introdurre probabilità), come nella fisica classica. Ad esempio, un elettrone
potrebbe essere descritto in modo completo determinando sia l’onda ψ che la posizione della
particella e stabilendo come queste due componenti interagiscano tra loro nel tempo (è l’idea
dell’“onda guidante” che aveva in mente lo stesso de Broglie). Tale interpretazione fu in effetti
tentata (in modo molto approfondito da Bohm, negli anni ’50) ed è nota come ipotesi delle
“variabili nascoste”, ma si è rivelata insoddisfacente per varie ragioni.
Oggi si ritiene invece che la funzione d’onda a un dato istante ψ(r) rappresenti tutto quello che è
possibile conoscere sullo stato corrente di una singola particella, e che può essere quindi usato per
poter fare previsioni sul suo futuro. Per questo essa viene chiamata, come abbiamo detto, stato
quantistico. Questo vuol dire che in generale le previsioni sul futuro, in meccanica quantistica, sono
sempre di carattere probabilistico. Non è possibile in alcun modo aggiungere ulteriori
informazioni, relative ad esempio alla posizione effettiva delle particelle, in modo da poter
prevedere il futuro in modo del tutto deterministico.
Da questo punto di vista, rispetto alla meccanica classica che ha l’ambizione di poter prevedere
univocamente il futuro se sono note perfettamente le condizioni iniziali, la meccanica quantistica
segna un passo indietro, una sorta di “rinuncia”: in generale il futuro è imprevedibile in meccanica
quantistica, anche conoscendo tutto quello che è possibile conoscere sulle condizioni iniziali del
sistema. E’ però ancora possibile fare delle precise previsioni probabilistiche sul futuro. Queste
previsioni possono essere poi verificate sperimentalmente eseguendo misure ripetute e facendo una
statistica dei risultati.
Anche se in linea di principio è più limitato della meccanica classica, il potere di previsione della
meccanica quantistica si è comunque rivelato straordinario, tanto da permetterci ad esempio di
penetrare i segreti degli atomi e delle particelle elementari, di progettare e costruire transistor e
laser, nonché di porre le basi per comprendere la quasi totalità dei fenomeni macroscopici.
5.5 Media e incertezza, o “indeterminazione”, sulla posizione di una particella
Come abbiamo detto, la posizione di una particella caratterizzata da una certa funzione d’onda ψ è
una variabile casuale, che obbedisce ad una distribuzione di probabilità fissata dalla funzione
d’onda in base alla (4.3) o (4.4).
In generale, data una qualsiasi distribuzione continua di probabilità dP/dx relativa ad una variabile
casuale continua x (la posizione nel caso di una particella in 1D) è utile introdurre le seguenti
definizioni (dove l’ultima espressione data in ciascuna definizione è valida per una funzione d’onda
ψ normalizzata, ossia deriva dalla sostituzione dP/dx = |ψ|2):
x =∫x
media (o valore atteso) della x:
media di una funzione f(x):
varianza della x:
Δx 2 =
f ( x) = ∫
(x − x
)
2
∞
dP
2
dx = ∫ x ψ ( x) dx (5.1)
dx
−∞
∞
dP
2
f ( x)
dx = ∫ f ( x) ψ ( x) dx (5.2)
dx
−∞
= ∫(x − x
)
2
∞
dP
dx = ∫ ( x − x
dx
−∞
)
2
ψ ( x) dx (5.3)
2
17
dove in tutte queste formule l’integrale va esteso a tutto il dominio di possibile variazione della
variabile casuale x (cioè da −∞ a +∞ nel caso della posizione della particella). Attenzione al fatto
che queste formule e tutte le altre formule che seguono in questo paragrafo sono valide
esclusivamente per una funzione d’onda ψ(x) normalizzata.
Non è difficile dimostrare (provateci) che la varianza può essere anche calcolata con la seguente
formula, spesso di utilizzo più conveniente:
varianza di x (formula alternativa): Δx 2 = x 2 − x
2
dP ⎞
⎛
dx ⎟ − x
= ⎜ ∫ x2
dx ⎠
⎝
2
=
(∫ x
2
)
ψ ( x) dx − x
2
2
(5.4)
Va notato che in meccanica quantistica, essendo la funzione d’onda ψ e quindi la densità di
probabilità dP/dx funzione anche del tempo, tutti questi parametri in generale dipendono dal tempo.
Qualitativamente, il valore medio fornisce una indicazione del “centro” della distribuzione. Il
significato statistico preciso di questo valore è il seguente. Eseguendo N misure ripetute sulla
variabile x (ad esempio la posizione della particella al tempo t dopo la preparazione), si otterranno i
valori casuali x1, x2, ..., xN. Si può dimostrare, sulla base della definizione della distribuzione di
probabilità, che nel limite in cui N→∞ la media aritmetica su tali misure tenderà proprio al valore
⟨x⟩ ottenuto secondo la (5.1), ossia che si ha
⎛1
x = lim ⎜
N →∞ N
⎝
⎞
N
∑ x ⎟⎠ (5.5)9
i =1
i
Come esempio, applicando la (5.1) al pacchetto d’onde gaussiano definito dalla (2.11) si ottiene ⟨x⟩
= x0. Usando l’espressione (2.12) del pacchetto gaussiano per tempi t diversi da zero, si ottiene
ovviamente ⟨x⟩ = x0(t).
La varianza, invece, fornisce una indicazione della larghezza della distribuzione, ossia di quanto
può tipicamente variare la x rispetto al suo valore medio ⟨x⟩. A partire dalla varianza si definisce
anche lo
scarto quadratico medio (o deviazione standard) della x: Δx = Δx 2 (5.6)
Anche lo scarto quadratico medio descrive la larghezza della distribuzione e quindi l’incertezza
con cui possiamo prevedere l’esito della misura. Il vantaggio rispetto alla varianza è che lo scarto
quadratico medio è espresso nelle stesse dimensioni ed unità di x. In meccanica quantistica, si usa
introdurre anche il termine “indeterminazione” per indicare l’incertezza (definita come scarto
quadratico medio). Nell’esempio del pacchetto d’onde gaussiano al tempo t = 0 (2.11), si ha Δx = σ,
mentre per tempi successivi si ha Δx(t) = σ′′(t).
Nel caso limite in cui Δx può essere considerato sempre molto piccolo rispetto alla precisione con
cui siamo in grado di misurare la posizione x, si può dire che la particella possiede una posizione
ben definita, entro gli errori sperimentali. Questo caso limite corrisponde ad una situazione
9
Anche in questo caso, la convergenza indicata in questa espressione va intesa in senso probabilistico, ossia la
probabilità di ottenere uno scarto maggiore di un valore dato, pur piccolo a piacere, tende a zero al divergere di N.
18
“classica”, cioè in cui la particella possiede una posizione definita anche nell’intervallo tra due
misure e non solo quando la posizione viene misurata. Ci dovremmo anche aspettare che la
meccanica quantistica approssimi le leggi della meccanica classica in questo caso limite, e in effetti
questo può essere dimostrato.
Passiamo ora al caso tridimensionale. A questo scopo dobbiamo generalizzare in modo ovvio le
espressioni (5.1)-(5.6) al caso di distribuzioni in più variabili casuali, cioè nelle tre coordinate x, y e
z della posizione di una particella. Possiamo definire il valore medio di ciascuna coordinata xi, dove
x1 = x, x2 = y e x3 = z, nel modo seguente:
coordinata media ⟨xi⟩ (ψ normalizzata):
xi =
∫ x ψ (r)
i
2
dV (5.7)
Ω∞
Raccogliendo in un singolo vettore le medie delle tre coordinate cartesiane x, y e z, si ottiene il
vettore posizione medio ⟨r⟩. La definizione di questo vettore può anche essere sintetizzata nella
seguente espressione:
vettore posizione medio della particella:
r (t ) = ∫ r ψ (r, t ) dV
2
Ω∞
(5.8)
dove abbiamo anche esplicitato la sua dipendenza dal tempo, derivante dalla dipendenza dal tempo
della funzione d’onda ψ.
Come nel caso 1D, il vettore posizione medio ⟨r⟩ è quello che rappresenta il centro della regione in
cui è probabile trovare la particella.
Lo scarto quadratico medio delle tre coordinate, ossia Δx, Δy e Δz, rappresentano invece, in tre
dimensioni, il grado di incertezza, o “indeterminazione”, sulla posizione della particella.
5.6 Misura della quantità di moto di una particella
Abbiamo quindi visto, nei paragrafi precedenti, che l’interpretazione probabilistica impone il fatto
che la funzione d’onda di una particella deve essere normalizzata, o almeno normalizzabile. Notate
che le onde armoniche non sono normalizzabili, perché l’integrale del loro modulo-quadro diverge.
Questo fatto non è altro che un’altra manifestazione, tra le tante, del fatto che le onde armoniche
possono solo essere considerate delle idealizzazioni, essendo infinitamente estese.
Le funzioni d’onda realistiche sono quindi sempre onde “finite”, ossia pacchetti d’onde o impulsi.
L’espressione (2.1) che descrive la dinamica di un pacchetto d’onde è valida solo per la particella
libera. Tuttavia, se consideriamo un istante di tempo fissato t, sarà comunque sempre possibile
esprimere matematicamente la funzione d’onda come integrale di Fourier, ossia si può comunque
porre:
funzione d’onda come integrale di Fourier: ψ ( x) =
∞
∫ a ( k )e
ikx
dk
(6.1)
−∞
(dove la dipendenza dal tempo della ψ e dei coefficienti a(k) è sottintesa).
19
La funzione a(k) corrisponde alla trasformata di Fourier della ψ(x) è data dalla seguente espressione
(in cui il tempo è sottinteso):
a (k ) =
1
2π
∞
∫ ψ ( x )e
− ikx
dx (6.2) 10
−∞
Queste due espressioni coincidono con la (2.1) e (2.2) per t = 0. Nel caso di particella libera, la
dinamica successiva è data dalla (2.1), il che corrisponde alla seguente particolare dinamica dei
coefficienti a(k):
dinamica della a(k) per la particella libera: a ( k , t ) = a(k , 0)e − iω ( k )t = a (k , 0)e −i
k 2t ( 2 m )
(6.3)
in cui la seconda espressione è ottenuta usando la relazione di dispersione (1.6). Nel caso più
generale in cui l’energia potenziale non si annulla la (6.3) dovrà essere sostituita da qualche altra
legge più complicata. Ma le relazioni (6.1) e (6.2) continueranno ad essere valide, istante per istante.
Un esempio specifico di pacchetto d’onde è quello gaussiano dato dall’espressione (2.11) (ancora
una volta, la dinamica successiva data dalla (2.12) è però valida solo nel caso di particella libera).
Un altro esempio forse più semplice sul piano matematico è il
⎧ 0
⎪
pacchetto d’onde rettangolare: ψ ( x) = ⎨ Aeik0 x
⎪ 0
⎩
per x < − L
per − L < x < L
(6.4) 11
per x > L
dove k0 è la frequenza spaziale dell’onda portante” e L la semi-larghezza spaziale del pacchetto. La
costante A che compare nell’espressione (6.4) dell’onda è fissata, in modulo, dalla condizione di
normalizzazione
∞
∫ ψ ( x)
−∞
2
dx = 2 A L = 1 ⇒
2
A=
1
2L
(6.5)
dove si è posto arbitrariamente uguale a zero l’argomento (o fase) dell’ampiezza complessa A.
Notate quindi che la condizione di normalizzazione è tipicamente quella che fissa il valore della
costante di ampiezza complessiva dell’onda (salvo per la fase arbitraria). Anche la costante N del
pacchetto gaussiano (2.11) risulta fissata dalla condizione di normalizzazione (provate a calcolarla
per esercizio).
Tornando al pacchetto rettangolare, non è difficile calcolare, utilizzando la (5.1), la posizione media
della particella, che risulta essere ⟨x⟩ = 0, come ci si poteva aspettare data la simmetria dell’onda. E’
La possibilità di definire trasformata ed integrale di Fourier è matematicamente garantita se la ψ(x) è integrabile in
modulo, come già riportato nel capitolo 2. Tuttavia, se la ψ(x) è “a quadrato sommabile” (ossia è integrabile in moduloquadro) come devono essere tutte le funzioni d’onda quantistiche, si dimostra che è comunque sempre possibile definire
trasformata ed integrale di Fourier nella forma data, purché gli estremi d’integrazione vengano estesi all’infinito con un
limite e in modo simmetrico (cioè si calcola il cosiddetto “valor principale” dell’integrale stesso).
11
Va notato tuttavia che anche il pacchetto d’onde rettangolare presenta aspetti di non completa realisticità, in quanto
possiede delle discontinuità nei punti x = ±L, ossia agli estremi del “rettangolo”.
10
20
anche agevole calcolare l’indeterminazione sulla posizione definita come scarto quadratico medio,
che risulta essere Δx = L / 3 .
Calcoliamo ora la trasformata di Fourier del pacchetto rettangolare utilizzando la (6.2):
a(k ) =
A sin ⎡⎣( k − k0 ) L ⎤⎦
π ( k − k0 )
(6.6),
cioè è molto simile alla trasformata del pacchetto d’onde rettangolare ottenuta nel paragrafo 2.5. La
(6.6) infatti descrive un “picco” centrato in k = k0, con una larghezza caratteristica Δk ≈ π/L. 12
Analogamente è possibile calcolare la trasformata di Fourier del pacchetto gaussiano (fatelo per
esercizio, usando i risultati del capitolo secondo).
Ora possiamo assumere che ad ogni onda armonica di frequenza spaziale k che entra nella
sovrapposizione di Fourier (6.1) corrisponda una quantità di moto p = ħk, secondo la legge di de
Broglie. Quindi, per un pacchetto d’onde, così come per qualsiasi funzione d’onda realistica e
quindi finita (o almeno normalizzabile), la particella non possiede una quantità di moto unica. Il
suo stato quantistico corrisponde invece ad una sovrapposizione di stati corrispondenti a diversi
valori della quantità di moto.
Questo aspetto appare chiaro matematicamente. Ma cosa significa invece, da un punto di vista fisico,
questa sovrapposizione di stati con diversa quantità di moto? Più concretamente, che valore troverò
se decido di misurare la quantità di moto della particella?
Una prima risposta a questa domanda è deducibile, oltre che direttamente dall’esperimento, anche
da un’analisi approfondita della definizione operativa della quantità di moto. La quantità di moto p
di una particella è infatti definita come il prodotto della massa m per la velocità v, ossia p = mv. Se
la massa è nota, la misura di quantità di moto si riduce quindi ad una misura di velocità della
particella. Ora una misura di velocità in generale si basa sulla misura successiva di due posizioni, in
modo da poter eseguire successivamente il rapporto tra spostamento (scalare o vettoriale) e
intervallo di tempo. Quindi la misura della velocità in ultima analisi si basa sulla misura di
posizione. Ora, il fatto che in meccanica quantistica una particella non abbia una posizione ben
definita nell’intervallo tra due misure porta naturalmente alla possibilità che la particella non abbia
in generale neanche una velocità ben definita, e quindi una quantità di moto. D’altra parte, ad ogni
stato quantistico (ossia istantanea della funzione d’onda ψ) si può associare una ben precisa
distribuzione di probabilità per le posizioni. Ci aspettiamo quindi che ad uno stato quantistico possa
essere associata anche una distribuzione di probabilità per le velocità o le quantità di moto
possibili della particella.
Infatti, se immaginiamo di eseguire una serie di misure ripetute della quantità di moto di particelle
preparate in modo da avere sempre la stessa funzione d’onda ψ, quello che succede è che si ottiene
ogni volta un valore ben preciso della quantità di moto p (a parte l’incertezza sperimentale), ma
questo valore cambia in modo casuale da una misura alla successiva.
12
La differenza tra la (6.6) e la (5.20) del capitolo 2 è dovuta semplicemente al fatto che il pacchetto d’onde considerato
nel paragrafo 2.5, definito dall’equazione (5.19) del capitolo 2, è scelto in modo da essere reale, per cui ha il coseno al
posto dell’esponenziale immaginario che appare nella (6.4).
21
Eseguendo un’analisi quantitativa delle frequenze con cui si verificano i diversi valori della quantità
di moto p, si scopre che la distribuzione di probabilità per i diversi valori di quantità di moto
misurati è fissata dallo stato quantistico della particella nel modo seguente:
dP
2
( p) ∝ a (k = p / ) (6.7)
dp
ossia è proporzionale al modulo quadro della trasformata di Fourier a(k) della funzione d’onda ψ.
Questo risultato appare abbastanza naturale, perché il modulo quadro |a(k)|2 fissa il “peso”,
all’interno della sovrapposizione (6.1), dell’onda armonica corrispondente a ciascuna quantità di
moto p = ħk. In realtà la (6.7) non è un nuovo principio della meccanica quantistica, perché può
essere dimostrato a partire dalla (4.7), riconducendo la misura di p a misure successive di posizione
della particella. Tuttavia, la dimostrazione è abbastanza complessa e la omettiamo.
Come nel caso della posizione, è possibile anche fissare la costante di proporzionalità che entra
nella (6.7) in modo da avere un’uguaglianza anziché una proporzionalità. La costante risulta fissata
dalla condizione di normalizzazione sulla distribuzione dP/dp, ossia che
∞
dP
∫ dp dp = 1
(6.8)
−∞
In particolare, se la funzione d’onda ψ(x) è normalizzata, si può verificare (omettiamo la
dimostrazione, puramente matematica) che la (6.8) è automaticamente soddisfatta ponendo
densità di probabilità per la quantità di moto p:
dP
2π
2
2
a( p / ) = A( p )
( p) =
dp
(6.9)
dove nella seconda uguaglianza abbiamo introdotto la seguente nuova funzione:
trasformata di Fourier della ψ (in termini di p): A( p ) =
2π
a( p
)=
1
2π
∞
∫ ψ ( x )e
− ipx /
dx
−∞
(6.10)
Questa funzione A(p) è in sostanza ancora la trasformata di Fourier della ψ(x), salvo per una diversa
scelta dei fattori 2π e per l’utilizzo della variabile p = ħk al posto di k. E’ possibile anche riscrivere
l’integrale di Fourier (6.1) in termini di questa funzione, come segue:
funzione d’onda come integrale di Fourier (in termini di p): ψ ( x) =
1
2π
∞
∫ A( p)e
ipx /
dp (6.11)
−∞
Si può notare come le (6.10) e (6.11) siano tra loro simmetriche e permettano di passare dalla ψ(x)
alla A(p) e viceversa, con una corrispondenza biunivoca perfetta.
Questa corrispondenza biunivoca, unita alla validità della (6.9) che lega immediatamente la
funzione A(p) alla distribuzione di probabilità per la misura della quantità di moto, conduce a
considerare la funzione A(p) come una diversa rappresentazione del medesimo stato quantistico
descritto dalla funzione d’onda ψ(x).
22
Notate che la dipendenza dal tempo di A(p) nel caso di una particella libera è data dal medesimo
fattore esponenziale complesso che appare nella (6.3), il che a sua volta implica che la distribuzione
di probabilità della quantità di moto dP/dp =|A(p)|2 è indipendente dal tempo, al contrario della
distribuzione di probabilità per la posizione. Questo fatto però non vale in generale.
Tirando le somme, abbiamo scoperto che in generale una particella in uno stato quantistico dato
ψ(x) non possiede né una posizione x, né una quantità di moto p ben determinate. Per entrambe
queste grandezze è invece nota la distribuzione di probabilità. Se la ψ(x) è normalizzata, allora la
densità di probabilità per la posizione x è data da |ψ(x)|2, mentre quella per la quantità di moto è
data da |A(p)|2, dove A(p) è fissata dalla ψ(x) mediante la trasformata di Fourier modificata (6.10).
Ovviamente, i parametri statistici definiti nel paragrafo 4 a proposito della posizione x possono
essere definiti anche per la quantità di moto p, utilizzando le definizioni (5.1)-(5.6), con p al posto
di x e con la distribuzione dP/dp = |A(p)|2. In particolare saranno definite in generale una quantità di
moto media ⟨p⟩ della particella e una indeterminazione Δp sulla quantità di moto.
Nell’esempio del pacchetto d’onde rettangolare (6.4), dalla (6.6) possiamo calcolare la A(p) e da
questa determinare la quantità di moto media che risulta essere ⟨p⟩ = ħk0, ossia la quantità di moto
associata alla frequenza centrale del picco. Se calcoliamo l’indeterminazione Δp, invece, in questo
particolare esempio otteniamo una divergenza, ossia si ha Δp = ∞ (anche se è comunque possibile
definire una “larghezza caratteristica” della distribuzione, ad esempio ponendo Δp = ħΔk = πħ/L,
corrispondente alla semi-larghezza del picco centrale della funzione A(p); questa e altre definizioni
alternative però non hanno il significato statistico di scarto quadratico medio). La divergenza dello
scarto quadratico medio Δp è in realtà causata dalle discontinuità che il pacchetto rettangolare
presenta ai bordi e che, come anticipato in nota, non sono realistiche fisicamente. Un pacchetto
d’onde realistico possiede sempre una indeterminazione Δp finita.
Il pacchetto d’onde gaussiano (2.11), ad esempio, possiede un’indeterminazione finita della quantità
di moto Δp. Un calcolo esplicito (fatelo per esercizio) fornisce il seguente risultato:
indeterminazione della quantità di moto di un pacchetto gaussiano: Δp =
2σ
=
2Δx
(6.12)
(attenzione però: nel caso di particella libera, questa indeterminazione resta costante, mentre la Δx
non è più data da σ ma da σ′′(t)).
5.7 Relazione di indeterminazione di Heisenberg
Abbiamo stabilito nei paragrafi precedenti che una particella in uno stato quantistico ψ(x) non
possiede né una posizione x, né una quantità di moto p ben precise. Per entrambe queste grandezze,
le misure restituiscono valori di volta in volta diversi, in modo casuale, ma obbedendo a due ben
precise leggi statistiche, |ψ(x)|2 e |A(p)|2, entrambe fissate dalla funzione d’onda ψ(x).
Nel capitolo secondo abbiamo visto che la larghezza spaziale di un’onda Δx e la larghezza di banda
che caratterizza la sua trasformata di Fourier Δk sono legate tra loro da una relazione del tipo ΔxΔk
= c, dove c è una costante numerica adimensionale (cioè senza unità) che dipende dalla forma
dell’onda e dalla definizione precisa delle due larghezze. Applicando questa relazione alle
distribuzioni di probabilità e moltiplicando per ħ ambedue i membri della relazione, ci aspettiamo
che in questo caso si abbia qualcosa del tipo
23
Δx Δp = cħ
(7.1)
Abbiamo anche annunciato nel capitolo secondo che la costante numerica c non può comunque
scendere sotto un certo valore minimo, circa unitario, ma che dipende in ogni caso dalla definizione
delle larghezze.
D’ora in avanti, adottiamo la definizione standard di scarto quadratico medio per le larghezze Δx e
Δp. In questo caso, è possibile dimostrare matematicamente (omettiamo la dimostrazione) che il
valore minimo possibile di c è esattamente ½, ossia che in generale vale la seguente
relazione di indeterminazione di Heisenberg:
ΔxΔp ≥
2
(7.2)
Tale importante relazione fu enunciata per la prima volta da Heisenberg, che le dà il nome, nel 1926.
Nel caso tridimensionale, la (7.2) viene sostituita con ovvia generalizzazione dalle seguenti tre
relazioni per ciascuna delle coordinate:
ΔxΔpx ≥
relazioni di indeterminazione di Heisenberg (3D): ΔyΔp y ≥
Δz Δpz ≥
2
2
(7.3)
2
In particolare la condizione di minima indeterminazione, ossia quella per cui il segno di maggioreuguale nella (7.2) viene sostituito da un uguale, si realizza nel caso di un qualsiasi pacchetto d’onde
gaussiano, ossia dato dall’espressione (2.11) (ma non da quello dato dall’espressione (2.12) che si
realizza per tempi successivi, se la particella è libera: perciò la condizione di minima
indeterminazione nella particella libera vale solo per un istante, ma non si mantiene nel tempo).
Le relazioni di indeterminazione di Heisenberg implicano che non è possibile avere una conoscenza
completa e perfetta simultaneamente della posizione e della quantità di moto (ossia della velocità)
della particella. Solo nel caso limite di un’onda piana, la quantità di moto p è perfettamente nota
senza incertezze. In questo caso limite, però, la distribuzione di probabilità |ψ(x)|2 per la posizione x
della particella è perfettamente piatta ed estesa a tutto lo spazio (Δx→∞), ossia non abbiamo alcuna
informazione, neanche parziale e probabilistica, su dove sia la particella. Se vogliamo restringere ad
una regione finita di spazio l’indeterminazione Δx sulla posizione della particella, siamo obbligati
ad introdurre il pacchetto d’onde e quindi perdiamo la completa conoscenza della quantità di moto.
Nel limite in cui la conoscenza sulla posizione della particella è molto precisa (ossia Δx→0), la sua
quantità di moto diventa completamente imprevedibile (Δp→∞). Nei casi intermedi abbiamo una
sorta di “compromesso” tra l’indeterminazione della posizione Δx e l’indeterminazione della
quantità di moto Δp.
La (7.2) è una conseguenza della natura ondulatoria della propagazione delle particelle, ed ha una
validità del tutto generale. La sua validità si fonda sul fatto che la funzione d’onda contiene la
massima conoscenza possibile sullo stato di moto della particella nell’intervallo tra due misure, o
tra la preparazione e la misura. Dato che nella (7.2) compaiono le indeterminazioni sulle grandezze
24
particellari x e p, la relazione di indeterminazione si presta particolarmente ad un confronto con la
situazione che si ha in meccanica classica. Infatti, la meccanica classica prevede che almeno in linea
di principio la posizione e la quantità di moto della particella sono entrambe conoscibili con
precisione arbitrariamente grande. Ci possono essere difficoltà di ordine pratico o tecnico a rendere
davvero piccole le indeterminazioni, ma non ci sono limiti fondamentali, imposti dalla fisica stessa.
Invece in meccanica quantistica c’è un limite invalicabile alla nostra possibilità di conoscere sia
posizione che quantità di moto (e quindi velocità), che nessun miglioramento della strumentazione o
trucco sperimentale permetterà mai di valicare, o la teoria stessa crollerebbe.
Attenzione a questa sottigliezza concettuale: in meccanica quantistica è impossibile conoscere
posizione e velocità con precisione arbitraria, non misurare tali grandezze. Sono due cose diverse:
“conoscere” richiede, ad esempio, la possibilità di “misurare” senza perturbare il sistema, in modo
da sapere in che stato si trova il sistema dopo la misura. In meccanica quantistica non ci sono limiti
fondamentali alla possibilità di misurare posizione e quantità di moto con precisione arbitraria,
anche simultaneamente, ma è impossibile usare tali misure per avere una conoscenza
arbitrariamente precisa di posizione e quantità di moto della particella dopo la misura, perché la
misura inevitabilmente perturba lo stato quantistico della stessa. Un altro modo per conoscere lo
stato del sistema è basato su una procedura di preparazione che garantisce che certe proprietà (ad
esempio posizione o quantità di moto) del sistema abbiano un certo valore. La relazione di
indeterminazione pone quindi anche un limite alla possibilità di preparare il sistema in modo che
abbia sia posizione che velocità fissati con precisione arbitraria.
Un semplice esempio mostra come la stessa natura quantistica di tutti gli oggetti protegga la validità
della (7.2). Supponiamo ad esempio di preparare una particella in uno stato quantistico
corrispondente ad una ben precisa quantità di moto p. In questo caso non si avrebbe alcuna
informazione sulla posizione r della particella (la funzione d’onda è un’onda piana armonica). Nel
tentativo di violare la (7.2), proviamo ora a misurare la posizione della particella in un modo
abbastanza “delicato” da non disturbare la quantità di moto. Se ci riuscissimo, verremmo a
conoscere sia la posizione che la quantità di moto e violeremmo la (7.2). Un modo diretto per
“guardare” dove sia la particella è di usare la luce. Un fascio luminoso illumina e viene quindi
diffuso dalla particella. Raccogliendo la luce diffusa con una lente, si può costruire un’immagine
della particella su uno schermo e capire così dove questa si trovi (l’occhio umano fa proprio questo:
una lente crea l’immagine degli oggetti sulla retina). Questo esperimento ideale è mostrato nella
seguente figura:
Esperimento per tentare di violare la relazione di indeterminazione di Heisenbergh
fascio luminoso (fotoni)
moto della
particella
apertura
angolare θ
luce diffusa
lente
schermo sensibile
al singolo fotone
asse x
25
Il problema è che la luce, per quanto possa essere “delicata”, perturba comunque il moto della
particella. Si può tentare di rendere più delicato l’effetto della luce abbassandone l’intensità.
Tuttavia, la luce è fatta di fotoni (qui entra in gioco la natura quantistica della luce) e diminuire
l’intensità corrisponde quindi solo a diminuire il numero di fotoni presenti. Se ci sono pochi fotoni,
diventa possibile che la particella attraversi il fascio di luce senza subire neanche una “collisione”
con i fotoni, per cui nessuna immagine appare sullo schermo e la posizione resta del tutto
indeterminata. Per determinare la posizione è necessario che almeno un fotone venga diffuso dalla
particella nello strumento ottico e raggiunga lo schermo (che immaginiamo essere una pellicola
sensibile anche ad un solo fotone). Se ciò avviene, veniamo a conoscere la posizione della particella
lungo la direzione x con una indeterminazione minima data nel migliore dei casi dal “potere
risolutivo” dello strumento ottico, Δx = λ/sinθ, dove λ è la lunghezza d’onda della luce usata e θ è
l’apertura angolare dello strumento ottico (si veda un testo di ottica o di fisica 2). D’altra parte, il
fotone trasporta una quantità di moto q = hν/c = h/λ, inizialmente diretta ortogonalmente all’asse x.
Dopo la collisione con la particella, il fotone ha cambiato direzione in modo sconosciuto. Per poter
essere catturato dalla lente, però, la sua direzione deve essere compresa nell’intervallo angolare ±θ.
Perciò la componente qx della quantità di moto del fotone dopo la collisione è indeterminata, ma è
compresa nell’intervallo ±(h/λ)sinθ. Dato che la quantità di moto totale si conserva, la particella
deve aver subito una variazione (dovuta al rinculo) di quantità di moto (lungo l’asse x) pari a –qx.
Perciò, la sua quantità di moto, inizialmente nota perfettamente, diventa indeterminata entro
l’intervallo Δp = (h/λ)sinθ. Il prodotto ΔxΔp dopo la collisione è quindi pari a h = 2πħ, e quindi
rispetta il principio di indeterminazione (7.2).
Notate che non è possibile migliorare le cose riducendo “il peso” di ogni singolo fotone
aumentandone la lunghezza d’onda. Infatti, in tal modo il contraccolpo subito dalla particella si
riduce e quindi si riduce l’indeterminazione finale sulla quantità di moto, ma l’indeterminazione
sulla posizione aumenta di un uguale fattore a causa della riduzione del potere risolutivo del sistema
ottico. Perciò il prodotto delle indeterminazioni resta uguale. Allo stesso modo, ridurre l’apertura
angolare del sistema ottico non aiuta.
Uno degli insegnamenti di questo esempio è che le misure che “tentano” di violare il principio di
indeterminazione sono inevitabilmente accompagnate da una perturbazione del sistema, che quindi
non resta uguale a prima. Al contrario di ciò che accadeva in meccanica classica, dove è concepibile
(almeno idealmente) seguire il moto di un sistema isolato misurandone tutte le proprietà senza
disturbarlo, in meccanica quantistica un sistema isolato non può essere “osservato” senza che
questa osservazione sia accompagnata da una perturbazione che ne “rompe l’isolamento” e ne
cambia il comportamento.
Con il paragrafo precedente abbiamo definito con maggiore chiarezza il legame tra la natura
particellare e quella ondulatoria di una particella materiale, come ad esempio l’elettrone. In pratica
la particella si comporta come tale al momento in cui viene misurata (in particolare per misure di
posizione, ma anche di energia e quantità di moto), e gli esiti possibili delle misure sono determinati
probabilisticamente dalla funzione d’onda. La particella si comporta invece come un’onda
nell’intervallo tra misure consecutive (o meglio, tra una “preparazione” e una misura, che non sono
del tutto equivalenti), ed in tale intervallo è governata deterministicamente dall’equazione di
Schroedinger. Quando non vengono misurate, le proprietà strettamente particellari, come la
posizione, perdono ogni reale significato fisico; oppure, almeno, non sono conoscibili in nessun
modo.
26
5.8 Funzioni d’onda come vettori a infinite dimensioni
Già nel secondo capitolo avevamo accennato alla possibilità di considerare le funzioni come vettori
ad infinite dimensioni. Si tratta di un’analogia puramente formale la cui comprensione non è
strettamente indispensabile per procedere nello studio della meccanica quantistica, ma che
costituisce un forte aiuto alla comprensione del formalismo alla base di tale teoria. Ovviamente, nel
paragonare le funzioni a vettori stiamo parlando di vettori astratti, che non hanno alcuna relazione
con i semplici vettori tridimensionali della fisica elementare. Tuttavia, un qualsiasi insieme di
“oggetti” matematici costituisce uno spazio vettoriale, e gli oggetti sono quindi denominati “vettori”,
se sono ben definite le operazioni di somma tra due oggetti e prodotto di un oggetto per un numero
“scalare” (ossia un numero normale, anche complesso) e queste due operazioni soddisfano alle
normali proprietà distributiva, associativa e commutativa. Le funzioni rispondono banalmente a tutti
questi criteri, per cui formano spazi vettoriali, detti anche spazi funzionali.
Una qualsiasi funzione ψ(x) può essere considerata come un vettore ad infinite componenti,
corrispondenti ai valori della funzione in ciascun punto x, proprio come un vettore normale è un
insieme discreto di numeri un (l’indice discreto n è sostituito dalla variabile continua x).
L’operazione di somma tra due funzioni, proprio come per i vettori, si riduce banalmente alla
somma componente per componente, ossia ψ1(x) + ψ2(x). L’operazione di moltiplicazione per un
numero c corrisponde alla moltiplicazione di tutte le componenti per quel numero, ossia cψ(x).
Come abbiamo detto, le funzioni d’onda di interesse fisico in meccanica quantistica sono solo
quelle normalizzate, ossia che soddisfano alla condizione (4.6) (o alla condizione (4.9) per il caso
3D). Tuttavia, l’insieme di funzioni normalizzate non costituisce uno spazio vettoriale, in quanto la
somma di due funzioni normalizzate non è necessariamente normalizzato. Inoltre, spesso in
meccanica quantistica conviene lavorare, nei calcoli intermedi, con funzioni d’onda ψ non
normalizzate, ma comunque “normalizzabili”, ossia per le quali l’integrale a primo membro della
(4.6) esiste, anche se non vale necessariamente 1. Queste funzioni per le quali esiste ed è finito
l’integrale del modulo-quadro in matematica sono dette funzioni a quadrato sommabile. L’insieme
di tutte le possibili funzioni a quadrato sommabile costituisce uno spazio vettoriale (o funzionale)
ben definito, detto spazio di Hilbert.
Per quanto detto, la natura di spazio vettoriale delle funzioni a quadrato sommabile è legata alla
validità delle seguenti proprietà, che qui enunciamo senza dimostrazione: (i) la somma ψ1+ψ2 di
due funzioni ψ1 e ψ2 ambedue a quadrato sommabile è ancora una funzione a quadrato sommabile;
(ii) il prodotto cψ di una funzione a quadrato sommabile ψ per un qualsiasi numero complesso c è
ancora una funzione a quadrato sommabile.
L’analogia tra le funzioni d’onda e i vettori può essere ulteriormente portata avanti introducendo un
opportuno prodotto scalare tra due funzioni d’onda. Sappiamo che il normale prodotto scalare tra
due vettori a e b viene definito come somma dei prodotti delle componenti corrispondenti, ossia a⋅b
= a1b1+a2b2+a3b3+...+aNbN. Quando si lavora con numeri e vettori complessi, questa definizione
deve essere modificata leggermente, nel modo seguente: a⋅b = a1*b1+a2*b2+a3*b3+...+aN*bN, ossia
bisogna utilizzare i complessi coniugati delle componenti del primo vettore. Notate che questo
rende il prodotto scalare dissimetrico tra i due vettori, ossia non commutativo. Si ha in particolare
a⋅b = (b⋅a)*. Per applicare questa definizione alle funzioni d’onda, la somma delle componenti deve
essere sostituita con un integrale, dato che l’indice di componente è sostituito con la variabile
continua x. Viene introdotto così il seguente
27
+∞
prodotto scalare tra funzioni (stati quantistici): ψ 1 ,ψ 2 = ∫ ψ 1∗ ( x)ψ 2 ( x)dx
(8.1)
−∞
dove si è scelto di utilizzare il simbolo ⟨,⟩ per indicare il prodotto scalare. Si dimostra che il
prodotto scalare (8.1) è ben definito e non diverge per qualsiasi coppia di funzioni a quadrato
sommabile. Esso soddisfa le proprietà che i matematici richiedono a un “buon” prodotto scalare,
che qui omettiamo.
Quando si introduce in uno spazio vettoriale un prodotto scalare, diventa possibile definire anche la
“norma” di un singolo vettore, ossia l’equivalente generalizzato della lunghezza o intensità dei
classici vettori tridimensionali. La lunghezza di un vettore tridimensionale può essere calcolata
come radice quadrata del prodotto scalare del vettore per se stesso. Analogamente, si ha la
norma quadra di una funzione (stato quantistico): ψ
2
= ψ ,ψ =
+∞
∫ ψ ( x)
2
dx (8.2).
−∞
Notate che il fatto che la funzione ψ sia a quadrato sommabile si traduce ora nel fatto che la sua
norma è sempre finita. Le funzioni d’onda normalizzate sono quelle di norma unitaria (sono
l’equivalente dei “versori”, o vettori unitari). Notate inoltre che la norma di una funzione d’onda
(come per un vettore) è un numero definito positivo (questo motiva il fatto che nel prodotto scalare
tra vettori complessi si prendono i complessi coniugati delle componenti del primo vettore). Se la
norma si annulla, questo implica che la funzione ψ è identicamente nulla (l’implicazione esatta
richiede di aggiungere alcune condizioni di continuità che qui omettiamo).
Un altro importante concetto che è possibile definire, una volta introdotto il prodotto scalare, è
quello di ortogonalità tra due funzioni. Due funzioni, ψ1 e ψ2, si dicono ortogonali tra loro se il loro
prodotto scalare si annulla:
ψ1 e ψ2 ortogonali:
ψ 1 ,ψ 2 = 0
∞
⇔
∫ψ
*
1
( x)ψ 2 ( x)dx = 0
(8.3)
−∞
Negli spazi vettoriali “normali” è sempre possibile individuare delle cosiddette basi. In uno spazio
vettoriale ad N componenti, una base è un insieme di N vettori e1, e2, ..., eN linearmente indipendenti
tra loro, e con la proprietà che un qualsiasi altro vettore u dello spazio vettoriale può essere scritto
sotto forma di combinazione lineare dei vettori di base, ossia:
N
u = c1e1 + c2e 2 + … + cN e N = ∑ cn e n
(8.4)
n =1
E’ inoltre sempre possibile determinare delle basi ortonormali, ossia i cui vettori sono tutti unitari
(di norma unitaria) e ortogonali tra loro. Queste due proprietà si sintetizzano nella seguente
espressione:
e n ⋅ e m = δ nm
(8.5)
28
dove δnm è il simbolo di Kronecker (δnm = 1 se n = m e δnm = 0 se n ≠ m). Se la base è ortonormale,
allora è facile verificare che i coefficienti che appaiono nella combinazione lineare (8.4) sono
calcolabili mediante la seguente semplice espressione:
cn = e n ⋅ u
(8.6)
In altre parole, con le basi ortonormali i coefficienti dello sviluppo coincidono con le proiezioni del
vettore u sui vettori di base. La dimostrazione di questa espressione si ottiene facilmente,
moltiplicando scalarmente ambedue i membri della (8.4) per il vettore di base en.
Analogamente, con le funzioni a quadrato sommabile è possibile individuare delle basi di funzioni e
queste possono essere prese tutte ortonormali tra loro, nel senso fissato dal prodotto scalare definito
prima. Nel caso delle funzioni, tuttavia, le basi sono composte da infiniti elementi, per cui la somma
che appare nella (8.4) deve essere sostituita da una serie, oppure addirittura un integrale se l’indice
n è sostituito da una variabile continua (o in alcuni casi una combinazione di una serie ed un
integrale). Limitiamoci per il momento al caso più semplice in cui l’indice della base è discreto.
Quindi la base è formata da una successione di infinite funzioni φn(x) (che sostituiscono i vettori en).
La (8.4) viene quindi sostituita dal seguente
∞
sviluppo della funzione d’onda in una base: ψ ( x) = ∑ cnφn ( x)
(8.7)
n =1
che vale per una qualsiasi funzione d’onda ψ (attenzione al fatto che a volte si utilizza un indice n
che inizia da 0 anziché 1). La base di funzioni può essere presa ortonormale, per cui si ha
l’equivalente della (8.5):
∞
φn , φm = ∫ φn* ( x)φm ( x)dx = δ nm
proprietà di ortonormalità delle autofunzioni:
(8.8)
−∞
In questo caso, i coefficienti dello sviluppo (8.7) possono essere ottenuti mediante proiezione sulle
funzioni di base, ossia si ha la seguente
formula per i coefficienti:
cm = φm ,ψ =
+∞
∫φ
∗
m
( x)ψ ( x)dx
(8.9)
−∞
Notate che in tutto questo paragrafo il tempo non è stato proprio considerato. La dipendenza dal
tempo delle funzioni d’onda ψ è stata lasciata sottintesa. Questo implica che tutte le relazioni
considerate vanno considerate come valide istante per istante. In particolare, ad esempio, i
coefficienti cn dello sviluppo (8.7) vanno considerati diversi per ciascun istante di tempo (ossia in
generale sono funzioni del tempo).
5.9 Valor medio di osservabili: il metodo degli operatori
Sfruttando il legame tra le funzioni d’onda ψ(x) e A(p), espresso dalle (6.10)-(6.11), è possibile
dimostrare che esiste una procedura semplificata per calcolare il valore medio della quantità di
moto p direttamente dalla ψ(x), senza cioè dover passare prima per il calcolo della trasformata A(p).
La dimostrazione è complessa e la omettiamo, ma la procedura non è difficile da imparare. Il punto
29
di partenza è l’introduzione di un operatore differenziale associato alla grandezza fisica quantità di
moto, definito come segue:
p̂ = −i
operatore differenziale “quantità di moto”:
∂
∂
(9.1)
=
∂x i ∂x
(come nel caso dell’operatore hamiltoniano, usiamo anche qui un “cappuccio” sopra il simbolo
della grandezza fisica per specificare che si tratta di un operatore). 13
Ora il valore medio della quantità di moto può essere calcolato utilizzando la formula seguente:
∞
quantità di moto media nello stato ψ: p = ∫ ψ ∗ ( x) pˆψ ( x)dx =
−∞
∞
i
∫ψ
−∞
∗
( x)
∂ψ
dx (9.2)
∂x
Notate che, essendo ψ*ψ = |ψ|2 = dP/dx, la (9.2) può essere considerata una generalizzazione della
(5.2): infatti, partendo dalla (5.2), dobbiamo scindere la densità di probabilità dP/dx nei due fattori
ψ* e ψ, inserire la grandezza fisica da mediare in mezzo tra questi due fattori, sotto forma di
operatore, anziché di funzione f(x), ed eseguire l’integrale.
La formula (9.2) può anche essere riscritta in forma più compatta utilizzando il prodotto scalare tra
funzioni introdotto nel paragrafo precedente, come segue:
quantità di moto media nello stato ψ: p = ψ , pˆψ
(9.3)
Questa espressione corrisponde al prodotto scalare della funzione ψ con la funzione p̂ψ ottenuta
applicando l’operatore p̂ alla stessa funzione ψ. Gli operatori sono infatti “oggetti matematici” che
“operano” sulle funzioni, trasformandole in altre funzioni.
Con lo stesso criterio può essere calcolata anche la media di una qualsiasi funzione della quantità di
moto, F = f(p). Bisogna innanzitutto considerare l’operatore differenziale associato a tale grandezza,
operatore associato alla grandezza F = f(p):
∂ ⎞
⎛
Fˆ = f ( pˆ ) = f ⎜ −i
⎟ (9.4)
∂x ⎠
⎝
e poi utilizzare tale operatore per ottenere la seguente
media della grandezza F = f(p) nello stato ψ:
∞
F = ψ , Fˆψ = ∫ ψ ∗ ( x) Fˆψ ( x)dx (9.5)
−∞
In particolare, questo metodo può essere utilizzato per calcolare l’indeterminazione Δp, sfruttando
l’identità (5.5), ossia
Δp =
p2 − p
2
(9.6)
13
Notate anche che l’operatore p̂ è proprio quello che, se applicato ad un’onda armonica, restituisce l’onda armonica
stessa, moltiplicata per il valore della quantità di moto p.
30
e calcolando la media ⟨p⟩ con la (9.2) e la media ⟨p2⟩ con la seguente espressione, corrispondente
alla (9.5) applicata al caso f(p) = p2:
∞
p
2
∞
⎛ ∂ ⎞
= ψ , pˆ 2ψ = ∫ ψ ∗ ( x) pˆ 2ψ ( x)dx = ∫ ψ ∗ ( x) ⎜
⎟ ψ ( x)dx = −
⎝ i ∂x ⎠
−∞
−∞
∞
2
2
∂ 2ψ
∫ ψ ( x) ∂x 2 dx (9.7)
−∞
∗
Quanto detto finora vale per la quantità di moto p o una sua funzione. Ma la procedura delineata è
in realtà del tutto generale: è cioè applicabile ad una qualsiasi grandezza fisica che abbia a che fare
con la particella. In meccanica quantistica, si usa il termine osservabile per riferirsi ad una
grandezza fisica misurabile. Consideriamo dunque un generico osservabile O, caratteristico del
sistema fisico considerato (la particella). A tale osservabile può essere sempre associato un
operatore funzionale Ô, ossia un oggetto matematico che trasforma una funzione in un’altra (non
sempre è un operatore differenziale). Una volta noto l’operatore, il valore medio dell’osservabile si
ottiene con la seguente formula generale:
∞
valore medio (o atteso) dell’osservabile O:
O = ψ , Oˆψ = ∫ ψ ∗ ( x)Oˆψ ( x)dx
(9.8)
−∞
Ad esempio, la procedura descritta si applica all’osservabile <<quantità di moto>> p, con
l’operatore differenziale dato dalla (9.1). Si applica anche all’osservabile <<posizione>> x,
utilizzando come operatore (non differenziale, in questo caso) la stessa variabile x, ossia l’operatore
agisce sulla funzione moltiplicandola per x, come indicato di seguito:
operatore posizione:
xˆψ ( x) = xψ ( x) (9.9)
Un qualsiasi osservabile definito come funzione di x, ossia O = f(x) viene associato ad un operatore
che agisce sulla funzione moltiplicandola semplicemente per f(x). Un osservabile funzione della
quantità di moto p invece viene associato ad un operatore differenziale definito dalla (9.4).
Ma gli osservabili possibili non si esauriscono in funzioni di x o funzioni di p. Come si procede in
questi casi? Nel caso più generale non esiste una regola certa per determinare tale operatore, che
deve quindi essere individuato con il confronto con gli esperimenti. Tuttavia, per molte grandezze
fisiche che possono essere espresse come funzione simultanea della posizione x e quantità di moto p
della particella, ossia O = f(x, p), la regola per trovare l’operatore è simile a quella data nella (9.4),
ossia bisogna sostituire al posto di p l’operatore differenziale p̂ dato dalla (9.1) nella funzione f.
Tuttavia, si presenta in questo caso un possibile aspetto problematico. Infatti, al contrario delle
variabili numeriche, in generale gli operatori non commutano, ossia uno scambio di ordine porta ad
un cambiamento del risultato.
Ad esempio l’operatore x̂ e quello p̂ non commutano tra loro, perché si ha
ˆ ˆψ = −i
px
∂
∂ψ
ˆˆψ
( xψ ) = −i ψ − i x = −i ψ + xp
∂x
∂x
(9.10)
Si può scrivere tale risultato anche con la seguente importante equazione operatoriale:
31
ˆˆ − px
ˆ ˆ = [ xˆ , pˆ ] = i
regola di commutazione per gli operatori x̂ e p̂ : xp
(9.11) 14
Questa proprietà fa sì ad esempio che la funzione f(x,p) = xp e la funzione algebricamente
equivalente f′(x,p) = px diano luogo ad operatori diversi, se applichiamo in ciascun caso la regola di
sostituzione p→ p̂ . In casi ambigui come questo, si è capito che la regola da utilizzare è la
seguente:
operatore associato ad osservabile O = f(x,p):
∂ ⎞
⎛
Oˆ = f s ( x, pˆ ) = f s ⎜ x,
⎟ (9.12)
⎝ i ∂x ⎠
dove la fs è la funzione f scritta in una forma algebricamente simmetrizzata per lo scambio di ordine
di x e p. Nell’esempio di f(x,p) = xp, la funzione simmetrizzata è fs = (xp + px)/2.
Una importante applicazione della (9.12) è il caso dell’osservabile energia. L’energia E di una
particella in 1D può essere sempre scritta sotto forma di funzione di posizione x e quantità di moto p
della particella. Tale funzione è detta funzione hamiltoniana H(x,p). Nel caso di una particella
soggetta ad una forza conservativa descritta dall’energia potenziale U(x), la funzione hamiltoniana è
data dalla seguente espressione:
funzione hamiltoniana di particella 1D soggetta a energia potenziale: H ( x, p) =
p2
+ U ( x) (9.13)
2m
Con questa espressione, possiamo trovare con la regola (9.12) l’operatore associato all’osservabile
energia (in questo caso non ci sono però problemi di simmetrizzazione, perché la funzione H è già
simmetrica), che risulta essere proprio l’operatore hamiltoniano Ĥ già introdotto nella (3.9).
A questo punto abbiamo anche una ricetta per determinare il valor medio dell’energia della
particella in un determinato stato quantistico, sulla base della (9.8), ossia
energia media in stato quantistico ψ:
∞
E = ψ , Hˆ ψ = ∫ ψ ∗ ( x) Hˆ ψ ( x)dx
(9.14)
−∞
Finora ci siamo concentrati solo sul calcolo del valor medio di un osservabile qualsiasi. Il valor
medio (atteso) di un osservabile corrisponde alla migliore previsione teorica della media di una
serie di misure ripetute dell’osservabile. Ma quello che ci servirebbe per un confronto completo con
gli esperimenti non è solo il valor medio, ma anche la distribuzione di probabilità per i diversi
valori possibili dell’osservabile. Infatti, come nel caso di posizione e quantità di moto, anche in
generale misurando un certo osservabile più volte si otterranno ogni volta valori diversi, in modo
casuale, ma obbedendo ad una distribuzione di probabilità fissata in qualche modo dallo stato
quantistico ψ. Sappiamo già come ottenere questa distribuzione solo per gli osservabili posizione x
(paragrafo 5.4) e quantità di moto p (paragrafo 5.6). Ma come si procede per gli altri osservabili? In
particolare, come si procede per l’energia? La risposta a queste domande verrà affrontata più avanti.
14
La non commutazione degli operatori x̂ e p̂ è collegata matematicamente alla relazione di indeterminazione di
Heisenberg tra i corrispondenti osservabili. In effetti, dati due osservabili qualsiasi A e B, è possibile dimostrare un
principio di indeterminazione generalizzato nella forma seguente: ΔAΔB ≥ ⎡ Aˆ , Bˆ ⎤ 2 , dove ΔA e ΔB sono le
⎣
⎦
ˆ
ˆ
indeterminazioni (definite come scarti quadratici medi) e A, B sono gli operatori associati ai due osservabili.
32
5.10 Stati quantistici stazionari e livelli di energia
Nei paragrafi precedenti ci siamo occupati delle previsioni probabilistiche che si possono fare a
partire dalla conoscenza dello stato quantistico, ossia della funzione d’onda ψ(x), ad un dato istante
di tempo.
Ora torniamo al problema di determinare la dinamica del sistema, ossia la dipendenza dal tempo
della funzione d’onda ψ(x,t). Sappiamo che l’equazione che governa tale dinamica è l’equazione di
Schroedinger dipendente dal tempo (3.8) (per il momento focalizziamo l’attenzione sul caso 1D,
generalizzeremo più avanti).
Come risolviamo questa equazione? Sappiamo che nel caso generale in cui c’è un’energia
potenziale U(x) non costante, le onde armoniche non sono soluzioni dell’equazione. Tuttavia,
dovrebbe essere ancora valido il metodo usato in precedenza di cercare innanzitutto i modi normali
del sistema, ossia le soluzioni che dipendono dal tempo in modo armonico con la stessa frequenza
dappertutto, per poi farne una opportuna combinazione lineare che dovrebbe fornire la soluzione
generale dell’equazione di Schroedinger. 15
Una funzione d’onda associata ad un modo normale dovrebbe essere descritta quindi dalla seguente
espressione:
funzione d’onda “modo normale”: ψ ( x, t ) = φ ( x)e − iωt (10.1)
Notiamo subito che in questi stati la distribuzione di probabilità per la posizione della particella
risulta essere indipendente dal tempo. Infatti si ha
dP
2
2
( x, t ) = ψ ( x , t ) = φ ( x )
dx
(10.2)
perché il modulo quadro dell’esponenziale immaginario vale 1. Non è difficile dimostrare che anche
la distribuzione di probabilità per la quantità di moto risulta indipendente dal tempo. E anche il
valore medio di un osservabile qualsiasi, calcolato in base alla (9.8), risulta costante nel tempo.
Per queste ragioni, una funzione d’onda “modo normale” data dall’espressione (10.1), in meccanica
quantistica prende normalmente il nome di stato stazionario, perché in tale stato tutte le grandezze
fisiche misurabili e le loro distribuzioni di probabilità risultano costanti nel tempo.
Un’altra cosa importante da notare è che la funzione d’onda “modo normale” data dall’espressione
(10.1) possiede una frequenza temporale (angolare) ω ben precisa. Applicando la prima relazione di
de Broglie, dobbiamo concludere che in uno stato stazionario l’energia del sistema possiede un
valore ben preciso, dato da E = ħω. Riesprimendo la (10.1) in termini dell’energia anziché della
frequenza, si ha la seguente espressione equivalente (e che preferiremo alla (10.1), nel seguito):
stato stazionario (modo normale):
ψ ( x, t ) = φ ( x)e −iEt /
(10.3)
15
La validità di tale metodo è in effetti legata al fatto che l’equazione sia omogenea nel tempo, ossia che non vi siano
coefficienti che dipendono dal tempo t. L’equazione di Schroedinger è a coefficienti non costanti, ma solo nella
variabile spaziale x. Perciò il metodo dei modi normali è applicabile.
33
Sostituendo la (10.3) nell’equazione di Schroedinger (3.8), e semplificando gli esponenziali
temporali comuni ad ambo i membri, otteniamo la seguente equazione, nota come
equazione di Schroedinger indipendente dal tempo (1D): −
d 2φ
+ U ( x)φ = Eφ
2m dx 2
2
(10.4)
(dove la derivata seconda parziale rispetto a x è stata sostituita da una derivata intera, dato che φ
dipende solo da x). Questa equazione è quella che ci permette di determinare gli stati stazionari per
ogni dato sistema fisico, cioè a seconda dell’energia potenziale U(x). Allo stesso tempo, l’equazione
(10.4) ci permette di determinare i valori possibili dell’energia E.
Come nel caso dell’equazione di Schroedinger dipendente dal tempo, introducendo l’operatore
hamiltoniano Ĥ, l’equazione (10.4) si può anche scrivere nella seguente forma compatta:
equazione di Schroedinger indipendente dal tempo (forma astratta): Ĥ φ = Eφ (10.5)
Questa forma astratta mostra con chiarezza che, come in tutti i casi visti in precedenza, anche in
questo caso l’equazione per i “modi normali” del sistema è un’equazione agli autovalori, in quanto
contiene come incognite le funzioni φ(x), che vengono dette autofunzioni o autostati e il valore E
dell’energia associata, che viene appunto detto autovalore. La (10.5) è anche formalmente analoga
alla (6.14) del capitolo 1 (con l’operatore Ĥ al posto della matrice A e le funzioni φ(x) al posto dei
vettori u), nonché alla (2.2) o (2.3) del capitolo 2 (con l’operatore Ĥ al posto dell’operatore  e le
funzioni φ(x) al posto delle u(x)).
L’equazione (10.4) o (10.5) va affiancata da una condizione supplementare di validità fisica delle
soluzioni, che restringe l’insieme di soluzioni accettabili rispetto all’insieme di soluzioni
matematiche possibili. In particolare in base a quanto detto in precedenza, ci aspettiamo che vada
imposta la condizione che le soluzioni φ(x) siano normalizzabili. In realtà, come vedremo, per
determinare correttamente la soluzione generale e i valori possibili dell’energia E devono essere
considerate anche le soluzioni non normalizzabili ma che costituiscano un caso limite,
opportunamente definito, di soluzioni normalizzabili dell’equazione di Schroedinger dipendente dal
tempo, come ad esempio le onde armoniche (che sono il limite di pacchetti d’onde normalizzabili,
per Δx→∞). Si può dimostrare che la seguente condizione permette di determinare sia le soluzioni
normalizzabili che questi casi limite:
condizione aggiuntiva di validità fisica delle soluzioni:
φ resta finita (non diverge) per tutti i valori di x e anche per x→±∞ (10.6)
La condizione (10.6) va combinata con l’equazione (10.4) o (10.5) per trovare gli autovalori
possibili E e le corrispondenti autofunzioni φ(x). Ovviamente, come negli altri problemi agli
autovalori, va esclusa anche la soluzione identicamente nulla φ(x) = 0, che matematicamente esiste
sempre, ma non ha alcun significato fisico.
L’equazione di Schroedinger (10.4) implica in generale che la funzione d’onda (o autofunzione)
φ(x) deve essere una funzione continua e con derivata prima dφ/dx continua. Infatti, se così non
fosse, ossia se ci fossero discontinuità della φ o della sua derivata prima, la derivata seconda d2φ/dx2
divergerebbe nei punti di discontinuità, il che sarebbe incompatibile con la finitezza degli altri
34
termini dell’equazione (10.4). 16 Questo risultato è particolarmente utile nei problemi in cui l’energia
potenziale U(x) presenta delle brusche discontinuità. Supponiamo ad esempio che l’energia
potenziale presenti una discontinuità nel punto x0. Risolvendo la (10.4), possiamo determinare la
soluzione dell’equazione di Schroedinger per ciascuna di due regioni adiacenti, che confinano nel
punto x0. Denominiamo φ1(x) e φ2(x) tali soluzioni, la prima che vale per la regione x ≤ x0, e la
seconda per x ≥ x0. Le condizioni di continuità enunciate prima ci consentono di “collegare” le due
soluzioni mediante le seguenti
φ1 ( x0 ) = φ2 ( x0 )
condizioni di raccordo nel punto di discontinuità x0 (con U(x) finita): dφ1
dx
=
x0
dφ2
dx
(10.7)
x0
Un’eccezione a queste condizioni di raccordo si ha quando da uno dei due lati della discontinuità,
oppure nel punto di discontinuità stesso, l’energia potenziale U(x) diverge. In questo caso, infatti, si
dimostra che condizione di continuità sulla derivata cade. In altre parole, nei punti in cui U(x)
diverge, la soluzione φ(x) resta continua, ma la derivata prima dφ/dx può subire discontinuità, per
cui nel collegare le soluzioni φ1 e φ2 va imposta solo la prima delle due equazioni (10.7).
Come vedremo più avanti, in alcuni sistemi fisici si trova che solo alcuni valori discreti dell’energia
E conducono a soluzioni della (10.4) che rispettano la condizione (10.6). In questi casi l’energia
risulta quantizzata, e i valori possibili dell’energia vengono anche detti livelli di energia (si parla
anche di spettro discreto di energie). In altri casi, invece, l’energia assume tutti i valori in un
intervallo continuo, per cui l’energia non è quantizzata (si parla anche di spettro continuo di
energie).
Come si vede, quindi, l’equazione di Schroedinger indipendente dal tempo in meccanica
quantistica svolge un doppio ruolo. Da un lato ci fornisce infatti gli stati stazionari del sistema
fisico, ossia l’equivalente dei modi normali della meccanica classica, con i quali possiamo costruire
la soluzione generale e determinare la dinamica del sistema (ossia risolvere l’equazione di
Schroedinger dipendente dal tempo), come vedremo meglio in seguito. Dall’altro, ci fornisce i
valori possibili dell’energia del sistema fisico e gli stati quantistici corrispondenti a tali valori, che è
un risultato importante in sé, indipendentemente dalla necessità di determinare la dinamica.
A questo punto ci potrebbe venire un dubbio. Nel paragrafo precedente, avevamo stabilito un
metodo per determinare il valore medio ⟨E⟩ dell’energia della particella in un qualsiasi stato
quantistico ψ, basato sull’operatore hamiltoniano Ĥ. Ora abbiamo introdotto un metodo
apparentemente del tutto diverso (che si basa sulla relazione di de Broglie e sulla frequenza
temporale) per determinare le energie possibili del sistema. Che relazione c’è tra questi due
approcci?
Vediamo innanzitutto il valore medio dell’energia in uno stato stazionario ψ dato dalla (10.3).
Applicando la (9.14) e utilizzando la (10.5) all’interno dell’integrale, otteniamo
∞
∞
∞
−∞
−∞
−∞
E = ψ , Hˆ ψ = ∫ ψ ∗ ( x) Hˆ ψ ( x)dx = ∫ ψ ∗ ( x) Eψ ( x)dx = E ∫ ψ ∗ ( x)ψ ( x)dx = E (10.8)
Quella enunciata non è ovviamente una vera dimostrazione rigorosa della continuità della φ, ma è comunque una
argomentazione che dà l’idea. La dimostrazione si può ottenere integrando una o due volte l’equazione (10.4) membro a
membro e sfruttando le proprietà di continuità degli integrali.
16
35
Questo significa che, in uno stato stazionario, il valore medio dell’energia determinato in base al
metodo dell’operatore hamiltoniano (cioè l’operatore associato all’osservabile energia) risulta
coincidere con il valore dell’energia dello stato stazionario determinato in base alla sua frequenza
temporale, tramite la relazione di de Broglie. Questo ci conforta sulla consistenza dei due metodi.
Ma possiamo andare oltre e calcolare anche l’indeterminazione (scarto quadratico medio)
sull’energia ΔE per uno stato stazionario, utilizzando la formula ΔE = ⟨E2⟩ − ⟨E⟩2 e calcolando la
media ⟨E2⟩ con la formula generale (9.8), dopo aver posto Ô =Ĥ2. Il risultato di tale calcolo è il
seguente
ΔE = ⟨E2⟩ − ⟨E⟩2 = E2 − E2 = 0
(10.9)
cioè l’indeterminazione sull’energia è nulla in uno stato stazionario. Questo conferma il fatto che,
in uno stato stazionario, l’energia assume un valore unico e ben determinato, come avevamo d’altra
parte anticipato sulla base del fatto che lo stato stazionario possiede una unica e ben precisa
frequenza temporale e che questa corrisponde all’energia, tramite la relazione di de Broglie. Anche
questa è quindi una conferma della consistenza dei due metodi.
5.11 Particella libera 1D: energie possibili e stati stazionari
Come primo esempio, consideriamo nuovamente la particella libera e vediamo se risolvendo
l’equazione di Schroedinger indipendente dal tempo (con la condizione aggiuntiva di validità fisica
delle soluzioni) riotteniamo quello che già sappiamo di tale sistema. In particolare dovremmo
ritrovare le onde armoniche come stati stazionari e le energie corrispondenti dovrebbero essere date
dalla relazione (1.5), cioè coprire tutti i valori positivi reali (cioè si ha uno spettro continuo di
energie).
Poniamo quindi U = 0 nella (10.4). Con pochi passaggi semplici, otteniamo la seguente equazione
differenziale ordinaria:
d 2φ 2mE
+ 2 φ =0
dx 2
(11.1)
Possiamo affrontare in generale questa equazione differenziale (essendo lineare e omogenea e a
coefficienti costanti) con il metodo degli esponenziali complessi. Cerchiamo quindi una soluzione
di prova del tipo
φ ( x) = Aeα x
(11.2)
dove α è un numero complesso da determinare e A è un’ampiezza complessa. Sostituendo tale
soluzione nella (11.1) e semplificando gli esponenziali otteniamo le seguenti soluzioni:
α =± −
2mE
2
(11.3)
(mentre l’ampiezza A resta indeterminata, come di consueto). Per procedere, dobbiamo ora
distinguere i seguenti tre casi: (i) E < 0; (ii) E = 0; (iii) E > 0.
36
Nel caso (i) (E < 0), si ha
α = ± χ con χ =
2m( − E )
2
(11.4)
cioè le due soluzioni di α risultano reali. Sostituendo tali risultati nella (11.2) otteniamo due
soluzioni indipendenti: φ(x) = Aeχx e φ(x) = Ae−χx. Dobbiamo ora verificare se queste soluzioni
soddisfano anche la condizione aggiuntiva di validità fisica (10.6). E’ banale verificare che la prima
diverge per x→∞ e la seconda diverge per x→−∞, per cui nessuna delle due è fisicamente valida.
In casi come questi dobbiamo però anche controllare che non sia possibile ottenere una soluzione
fisicamente valida con una combinazione lineare delle due soluzioni, perché può accadere che una
opportuna combinazione lineare di due (o più) soluzioni non fisicamente valide sia fisicamente
valida.
Perciò consideriamo anche la seguente combinazione lineare:
φ ( x) = Ae χ x + Be− χ x
(11.5)
E’ facile verificare che per qualsiasi scelta di A e B (salvo quella banale A = B = 0, che però non
corrisponde ad una soluzione valida) la (11.5) diverge per x → ±∞. Perciò anche la combinazione
lineare non è fisicamente valida. Quindi non esistono soluzioni con energia negativa, in accordo con
quanto già sapevamo.
Passiamo ora al caso (ii), cioè E = 0. In questo caso, la (11.3) fornisce α = 0, da cui si ha la
soluzione φ(x) = A. Però in questo caso il metodo degli esponenziali non basta perché fornisce una
sola soluzione indipendente, invece di due (ne servono due perché l’equazione è del secondo
ordine). In questi casi “critici”, sappiamo che possiamo usare come seconda soluzione
l’esponenziale moltiplicato per la variabile, ossia φ = Axeαx = Ax. D’altra parte la (11.1) può anche
essere risolta banalmente con una doppia integrazione indefinita, che fornisce la seguente soluzione
(che è già la combinazione lineare delle due soluzioni indipendenti menzionate):
φ ( x) = A + Bx
(11.6)
Imponendo ora la condizione di validità fisica (10.6), troviamo che deve essere B = 0 per evitare
divergenze per x → ±∞. Perciò la soluzione trovata si riduce ad una funzione d’onda costante
φ(x) = A
(11.7)
Questa è una soluzione non normalizzabile, ma soddisfa alla condizione di validità fisica (il che
vuol dire che è un caso limite ben definito di una soluzione normalizzabile). Infatti, una funzione
d’onda costante è anche un caso particolare di onda armonica con k = 0 (e quindi ω = 0) e le onde
armoniche sono casi limite di pacchetti d’onde molto estesi. Ne concludiamo che l’energia nulla, E
= 0, è un’energia fisicamente possibile per una particella libera (classicamente essa corrisponde ad
una particella ferma) e ad essa corrisponde una sola autofunzione, data dalla (11.7).
Passiamo infine al caso (iii), cioè E > 0. In questo caso la (11.1) non è altro che la solita equazione
dell’oscillatore armonico (perché il segno della costante davanti a φ è positivo), per cui già
conosciamo bene le sue soluzioni. D’altra parte, procedendo comunque con il metodo degli
esponenziali complessi, la (11.3) fornisce ora le seguenti due soluzioni immaginarie pure:
37
α = ±ik con k =
2mE
2
(11.8)
Sostituendo tali risultati nella (11.2) otteniamo le seguenti due soluzioni indipendenti (esponenziali
complessi),
φ ( x) = Aeikx
φ ( x) = Be −ikx
(11.9)
Queste due soluzioni indipendenti soddisfano entrambe la condizione di validità fisica (10.6), per
cui sono entrambe valide (e ovviamente lo è anche la loro combinazione lineare).
Abbiamo trovato quindi non una, ma due soluzioni fisicamente valide e indipendenti per ciascun
valore positivo dell’energia E. Quindi tutti i valori reali con E > 0 sono energie possibili del
sistema. Ad ogni energia sono associate due autofunzioni indipendenti. In generale la presenza di
due o più autofunzioni per uno stesso autovalore è detta degenerazione. In questo caso si parla di
degenerazione dell’energia. Il numero di autofunzioni indipendenti viene chiamato grado di
degenerazione del livello di energia considerato (o più brevemente solo “degenerazione” del livello
di energia), che in questo caso è pari a 2.
Tirando le somme, abbiamo stabilito che per una particella libera quantistica lo spettro delle energie
possibili è come nel caso classico l’insieme di tutti i valori non negativi, ossia E ≥ 0. La particella
libera è un caso di sistema fisico in cui si ha uno spettro continuo di energie, non quantizzato.
L’energia minima è E = 0, che corrisponde ad una energia cinetica nulla come nel caso classico
(particella ferma). Inoltre abbiamo visto che per E = 0 non si ha degenerazione, mentre per tutti i
valori strettamente positivi E > 0 si ha degenerazione doppia.
E’ facile verificare inoltre, sostituendo le autofunzioni φ(x) trovate (11.9) (che si riducono entrambe
alla (11.7) nel caso E = 0) nella espressione (10.1) o (10.3) per gli stati stazionari ψ(x,t) completi di
dipendenza dal tempo, che gli stati stazionari della particella libera coincidono proprio con le onde
armoniche, come ci aspettavamo.
Infine, la relazione (11.8) che lega l’energia E e quindi la frequenza ω = E/ħ alla costante k che
compare come numero d’onde nelle autofunzioni (11.9) è proprio la stessa della relazione di
dispersione (1.6) che avevamo inizialmente postulato a partire dalla relazione tra energia e quantità
di moto per una particella libera e dalle relazioni di de Broglie. Quindi anche la relazione di
dispersione è correttamente ritrovata, come ci dovevamo aspettare.
E’ molto utile, per quello che ci aspetta in seguito, fare l’esercizio (fatelo!) di ripetere tutti i
ragionamenti e i calcoli di questo paragrafo assumendo che ci sia ora un’energia potenziale diversa
da zero ma costante, ossia U = U0 ≠ 0. Come è facile verificare, tutte le formule trovate restano
valide se sostituiamo la differenza E − U0 al posto di E.
5.12 Particella in buca di potenziale rettangolare infinita
Un altro caso interessante e particolarmente semplice da risolvere è la cosiddetta buca di potenziale
rettangolare infinita, a volte indicata anche come “scatola”.
38
In pratica, essa si realizza assumendo che vi sia una energia potenziale nulla (o anche costante)
all’interno di un certo intervallo spaziale e infinita al suo esterno. Consideriamo ad esempio una
buca localizzata nell’intervallo (0, L) dell’asse x. L’energia potenziale è data dalla seguente
espressione:
x<0
⎧∞ per
⎪
U ( x) = ⎨ 0 per 0 ≤ x ≤ L
⎪∞ per
x>L
⎩
(12.1)
In termini di forze, questa energia potenziale corrisponde ad una forza nulla all’interno della buca e
una forza infinitamente intensa e che spinge la particella all’interno della buca quando questa si
trova adiacente alle “pareti”, ossia in x = 0 e x = L. Perciò, da un punto di vista classico, è come se
ci fossero due muri infinitamente rigidi che confinano la particella all’interno della buca.
Questo è il primo esempio di una classe di problemi particolarmente semplici della meccanica
quantistica, caratterizzati da un’energia potenziale costante a tratti (ossia costante in regioni
limitate di spazio, con delle discontinuità nei punti di contatto). Per risolvere l’equazione di
Schroedinger indipendente dal tempo (10.4) in questo tipo di problemi, è possibile procedere nel
modo seguente: (i) si risolve l’equazione (10.4) in ciascuna regione in cui U(x) è costante; (ii) si
impongono alle soluzioni così trovate le condizioni di raccordo (10.7) in ciascun punto di
discontinuità dell’energia potenziale.
Iniziamo quindi a risolvere la (10.4) nelle regioni esterne alla buca, in cui U = ∞. Questo caso non è
però ben definito matematicamente. E’ ragionevole ritenere che se U → ∞ in un intervallo finito di
spazio, la funzione d’onda φ si debba annullare in quell’intervallo, perché altrimenti vi sarebbe un
termine infinito Uφ nell’equazione di Schroedinger (10.4) che non potrebbe essere compensato
dagli altri termini. Questa conclusione può essere anche dimostrata rigorosamente, ma omettiamo la
dimostrazione. Quindi, nella buca infinita, la funzione d’onda φ si deve annullare all’esterno della
regione di confinamento, ossia φ(x) = 0 per x < 0 e per x > L. Questo a sua volta significa che una
qualsiasi misura della posizione della particella la troverà sempre localizzata all’interno
dell’intervallo (0, L), proprio come avviene nel caso classico.
All’interno della buca si ha U = 0, per cui possiamo usare lo stesso calcolo usato nel paragrafo
precedente relativo alla particella libera. In particolare, per E > 0 abbiamo ancora una volta le
soluzioni (11.9), con k dato dalla (11.8). Quindi complessivamente, abbiamo la seguente soluzione:
per
⎧φI ( x) = 0
⎪
φ ( x) = ⎨φII ( x) = Aeikx + B − ikx per
⎪φ ( x) = 0
per
⎩ III
x<0
0≤ x≤L
(12.2)
x>L
Ora però, dobbiamo applicare le condizioni di raccordo nei punti x = 0 e x = L, in cui l’energia
potenziale ha una discontinuità. Dato che l’energia potenziale diverge da un lato di questi punti, va
imposta solo la condizione di continuità della funzione d’onda φ e non della sua derivata, ossia solo
la prima delle (10.7). Cioè in questo caso le condizioni di raccordo si traducono nelle seguenti
condizioni al contorno:
φII (0) = 0
φII ( L) = 0
(12.3)
39
relative all’espressione della φ(x) valida nell’interno della buca quantistica. Vediamo quindi che, da
un punto di vista ondulatorio, la buca quantistica infinita si comporta come un risonatore classico.
Applicando la prima delle condizioni (12.3), otteniamo B = −A, per cui la funzione d’onda
all’interno della buca diventa la seguente:
φ2 ( x) = A′ sin(kx) (12.4)
dove abbiamo introdotto la nuova costante A′ = 2iA.
Applicando alla (12.4) la seconda delle condizioni al contorno (12.3), otteniamo la solita condizione
sui numeri d’onde k possibili nel risonatore, ovvero sulle lunghezze d’onda possibili per gli elettroni
nella buca:
sin(kL) = 0 ⇔ kL = nπ
⇔ nλ = 2 L
(12.5)
Questa condizione, combinata con la relazione di dispersione (11.8) che lega k all’energia E (o con
la (1.5) insieme alle relazioni di de Broglie, che è equivalente) fornisce le energie possibili:
energie possibili (autovalori) nella buca infinita:
En =
π2
2
2mL
2
n2
con n = 1, 2,... (12.6)
In questo caso, quindi, si ha uno spettro di energie discreto, ossia un’energia quantizzata. Il numero
n utilizzato per indicizzare l’energia prende il nome di numero quantico. Ad ogni valore di n
corrisponde l’energia data dalla (12.6) e la funzione d’onda (autofunzione) data dalla (12.4) con la
sostituzione di k con il valore calcolato dalla (12.5). Queste funzioni d’onda sono normalizzabili,
per cui, imponendo la condizione di normalizzazione (4.9), fissiamo anche il valore della costante
moltiplicativa A′ (almeno in modulo). In conclusione, abbiamo le seguenti
autofunzioni della buca infinita (per 0 ≤ x ≤ L):
φn ( x) =
2
⎛ nπ x ⎞
sin ⎜
⎟
L
⎝ L ⎠
(12.7)
(ovviamente la funzione d’onda è completata da φn(x) = 0 per x < 0 e per x > L). L’espressione
(12.7) chiarisce anche perché n = 0 non è un numero quantico ammissibile, perché rende nulla la
funzione d’onda. Inoltre, numeri n negativi restituiscono la stessa funzione d’onda del loro numero
opposto −n, a meno di un ininfluente cambiamento di segno (ricordate che la funzione d’onda è
sempre definita a meno di un fattore di fase qualsiasi). Per questi motivi si ha n = 1, 2, ..., ossia in
questo caso n è limitato ai numeri naturali (ma questa proprietà non è generale per tutti i numeri
quantici, dipende dal sistema quantistico). Il fatto che vi sia una sola autofunzione indipendente per
ciascun valore dell’energia corrisponde a dire che nella buca quantistica (1D) l’energia non
presenta degenerazione.
Possiamo anche reinserire nelle funzioni d’onda la dipendenza dal tempo, utilizzando la (10.3).
Otteniamo così:
stati stazionari della buca infinita (per 0 ≤ x ≤ L): ψ n ( x, t ) =
2
⎛ nπ x ⎞ −i Ent
sin ⎜
⎟e
L
⎝ L ⎠
(12.8)
dove i valori En sono sempre dati dalla (12.6).
40
L’analisi compiuta finora è limitata al caso E > 0. Tuttavia, ripercorrendo gli stessi passi nei casi in
cui E ≤ 0, si verifica che le condizioni al contorno (12.3) escludono l’esistenza di soluzioni non
nulle. Perciò non esistono autofunzioni con E ≤ 0 e lo spettro dato nella (12.6) è quello totale.
La quantizzazione dell’energia che abbiamo visto in questo esempio mostra in modo semplice come
effettivamente funzioni nella meccanica quantistica ondulatoria l’idea originaria di de Broglie di
ottenere la quantizzazione dell’energia degli elettroni negli atomi mediante la corrispondenza con il
risonatore di onde di materia. Notate però che nel nostro risonatore quantistico l’energia è
proporzionale al quadrato di n, anziché ad n, per cui le energie (e le frequenze temporali) non sono
multiple intere di una energia fondamentale. Questa differenza con il caso del normale risonatore di
onde che obbediscono all’equazione di D’Alembert è dovuta alla diversa relazione di dispersione.
L’energia minima della particella nella buca si ha per n = 1, ossia E = E1. Lo stato di energia
minima è detto stato fondamentale del sistema. Tale stato assume spesso un’importanza particolare
perché è l’unico stato del tutto stabile, in quanto negli altri stati è sempre possibile una transizione
quantistica con emissione di un fotone (come quelle dell’atomo di Bohr), ed è anche quello in cui si
porta sempre la particella a temperature sufficientemente basse.
A proposito dell’energia minima, è interessante notare che, mentre classicamente una particella in
una buca di potenziale come quella considerata possiede una energia minima nulla, corrispondente
cioè ad una particella ferma in un punto qualsiasi della buca, nel caso quantistico l’energia minima
è E1 = (πħ)2/(2mL2) > 0 ed è tutta energia cinetica, dato che nella buca si ha U(x) = 0. Questa
energia cinetica minima (misurata a partire dal valore minimo dell’energia potenziale) è detta
anche “energia di punto zero”. Se la particella possiede sempre un’energia cinetica diversa da zero,
si può dire che non è mai del tutto ferma. Questa “agitazione quantistica” delle particelle esiste
anche a temperature molto basse (arbitrariamente prossime allo zero assoluto), quando la normale
agitazione termica dovuta all’interazione con l’ambiente scompare. Notate che anche se la particella
possiede un “moto di punto zero”, rivelato dalla sua energia non nulla, la distribuzione di
probabilità per la sua posizione |ψ1(x,t)|2 = |φ1(x)|2 resta comunque costante nel tempo, come per
tutti gli stati stazionari.
Ricordate che invece la particella libera non ha un’energia di punto zero, cioè l’energia cinetica
minima è nulla. In effetti, l’energia di punto zero è una caratteristica generale dei sistemi in cui la
particella viene confinata in una regione limitata dello spazio. Una spiegazione qualitativa di
questo fatto può essere basata sul principio di indeterminazione: se la particella è confinata in una
regione di estensione L, la sua posizione è indeterminata per un Δx ≈ L, e perciò anche la sua
quantità di moto deve essere indeterminata almeno per Δp ≈ ħ/Δx = ħ/L. Per essere indeterminata, p
non può annullarsi (altrimenti sarebbe perfettamente nota). Il valore medio di p deve essere pari a
circa Δp/2, per cui si ha p ≈ ħ/(2L). Quindi l’energia è almeno pari a E ≈ p2/2m = ħ2/8mL2, che è
dello stesso ordine di grandezza di E1.
5.13 Misure di energia o di altri osservabili e corrispondente distribuzione di
probabilità
Che significato fisico dobbiamo dare ad uno spettro discreto di energie En (con n = 1, 2, ...) di un
sistema quantistico come quello ottenuto nel paragrafo precedente? La risposta è la seguente: una
qualsiasi misura precisa dell’energia (totale) della particella restituisce necessariamente uno dei
valori En, ossia uno dei “livelli di energia” del sistema, e non può invece mai restituire un valore
intermedio tra due livelli consecutivi. Ma quale valore in particolare verrà misurato?
41
Nel caso la particella al momento della misura si trovi proprio in uno stato quantistico stazionario
ψn (x,t) di energia definita En, la risposta in un certo senso la conosciamo già. La misura deve
restituire necessariamente il valore En (entro l’incertezza sperimentale). Anche il valore medio ⟨E⟩
dell’energia è pari a En, in base a quanto abbiamo detto nel paragrafo 10.
Ma se la particella non occupa proprio uno degli stati stazionari, cosa succede? Se la sua funzione
d’onda (ad un certo istante di tempo fissato) è ad esempio ψ(x) e questa funzione non coincide con
nessuna delle autofunzioni φn(x) dell’energia (anche a meno della costante di fase arbitraria)? Quale
sarà allora il valore dell’energia misurata?
Non dovrebbe sorprendere che, come avviene per la misura di posizione e quella della quantità di
moto, anche nel caso della misura dell’energia della particella i risultati saranno casuali. Ossia,
ripetendo la misura più volte, “uscirà” ogni volta un valore diverso dell’energia misurata, a caso. I
valori di energia che possono “uscire” sono comunque sempre e soltanto gli En dello spettro di
energie del sistema. Notate che in questo caso il valore medio ⟨E⟩ può anche non coincidere con
nessuno dei valori En, proprio come la media dei risultati del lancio di un dado è pari a 3.5, ma
nessuna delle facce riporta questo valore.
Ma qual è la probabilità di ciascun valore di energia? Per analogia con il caso della misura di
posizione e di quantità di moto, dobbiamo aspettarci che la funzione d’onda ψ(x) determini le
probabilità dei diversi valori possibili di energia, in caso di sua misura. Ricordiamo che nel caso
della misura di quantità di moto, la (densità di) probabilità era determinata (tramite il moduloquadro) dall’ampiezza A(p) [o a(k)]dei coefficienti che entrano nella combinazione lineare
(integrale di Fourier) che descrive la ψ(x) come sovrapposizione di onde armoniche (stati di
quantità di moto perfettamente definita).
La situazione ora è molto simile. Sappiamo che gli stati stazionari sono modi normali del sistema,
per cui ci aspettiamo che un qualsiasi stato quantistico ψ(x) possa essere scritto come combinazione
lineare dell’insieme di tutti gli stati stazionari. Questa combinazione lineare dovrebbe darci anche la
dinamica quantistica, e questo lo vedremo nel prossimo paragrafo. Per il momento, ci focalizziamo
invece su un solo istante di tempo (ad esempio t = 0), che lasciamo implicito.
Dovrebbe quindi essere sempre possibile scrivere la seguente espressione:
∞
stato quantistico come combinazione di autostati dell’energia: ψ ( x) = ∑ cnφn ( x) (13.1)
n =1
Confrontando la (13.1) con la (8.7), vediamo che l’insieme di autostati dell’energia φn(x) deve
costituire una base dello spazio delle funzioni d’onda fisicamente ammissibili ed in particolare delle
funzioni d’onda normalizzabili. E’ possibile dimostrare anche che tali funzioni φn(x) sono a due a
due ortogonali, se relative ad energie diverse (mentre possono essere sempre scelte in modo da
essere ortogonali, se sono relative alla stessa energia). Questo implica che la base delle funzioni
φn(x) è una base ortonormale. Tutto questo è del tutto generale, ossia in qualsiasi sistema
quantistico l’insieme di tutte le autofunzioni dell’energia forma una base ortonormale nello spazio
di tutte le funzioni d’onda normalizzabili.
Il fatto che la base φn sia ortonormale ci fornisce un metodo immediato per determinare i
coefficienti cn dello sviluppo, utilizzando l’espressione (8.9). A questo punto, per analogia con il
caso della quantità di moto, ci aspettiamo che il modulo quadro dei coefficienti cn che appaiono
42
nella combinazione lineare (13.1) restituisca le probabilità Pn dei diversi valori possibili En
dell’energia, se questa viene misurata. E in effetti è proprio così, si ha cioè la seguente espressione:
probabilità di ottenere En misurando l’energia in stato ψ: Pn = cn = φn ,ψ
2
2
2
∞
=
∫ φ ( x)ψ ( x)dx
*
n
−∞
(13.2)
(in questa espressione, l’uguaglianza stretta in realtà vale solo se ψ e tutte le φn sono normalizzate,
altrimenti la relazione si riduce ad una semplice proporzionalità). Notate che ora abbiamo a che fare
con probabilità riferite a ciascun valore, e non densità di probabilità, perché la variabile energia è
discreta e non continua. Nel caso di spettro continuo dell’energia si torna a parlare di densità di
probabilità.
Va precisato anche che l’espressione (13.2) vale strettamente solo se gli stati φn sono tutti relativi ad
energie diverse (come nella buca infinita), ossia non c’è degenerazione. Nel caso più generale, la
(13.2) può essere ancora intesa come la probabilità che la particella venga “trovata nello stato φn”.
Se più autostati sono riferiti allo stesso valore dell’energia, la probabilità associata a quell’energia
sarà poi semplicemente la somma delle probabilità.
Notate che la (13.2) ha anche una semplice interpretazione “geometrica”. La probabilità di ritrovare
la particella nello stato φn se inizialmente questa si trova nello stato ψ è data dal modulo-quadro del
prodotto scalare tra le due funzioni, ossia dal quadrato della proiezione dell’una sull’altra.
Come nel caso della misura di quantità di moto, anche la (13.2) non è un nuovo principio della
meccanica quantistica, perché può essere dimostrata a partire dalla interpretazione statistica della
funzione d’onda ψ(x), ossia dalla (4.4). Tuttavia, omettiamo la dimostrazione.
Quanto detto a proposito dell’energia è in realtà generalizzabile ad un osservabile qualsiasi.
Accenniamo appena alla cosa, su cui torneremo più avanti. Dato un qualsiasi osservabile O e il suo
operatore associato Ô, l’insieme di valori possibili dell’osservabile (spettro dell’osservabile) è
definito risolvendo l’equazione agli autovalori ed autofunzioni (analoga all’equazione di
Schroedinger indipendente dal tempo):
ˆ ( x) = λ f ( x)
equazione agli autovalori dell’osservabile O: Of
(13.3)
Immaginiamo di aver risolto questa equazione e di aver determinato uno spettro, che per semplicità
assumiamo essere discreto e non degenere (cioè ad ogni λn corrisponde una e una sola fn), ossia
valori possibili dell’osservabile O: λ1, λ2, ..., λn, ...
corrispondenti autofunzioni:
f1(x), f2(x), ..., fn(x), ...
E’ un postulato della meccanica quantistica il fatto che l’insieme delle autofunzioni di un qualsiasi
osservabile costituisce sempre una base ortonormale dello spazio delle funzioni d’onda fisicamente
valide (anche se va tenuto presente che se O non è proprio l’osservabile “energia”, le autofunzioni fn
non sono stati stazionari e quindi neanche “modi normali” del sistema). E’ quindi possibile sempre
scrivere una combinazione lineare analoga alla (13.1) o alla (8.7) con le autofunzioni fn al posto
delle φn e i coefficienti saranno sempre dati dalla (8.9). Infine, in caso di misura dell’osservabile O,
la probabilità associata a ciascun valore λn sarà data dalla seguente espressione
43
probabilità P(O = λn) per misura in stato ψ: Pn = cn = f n ,ψ
2
2
∞
=
∫
2
f ( x)ψ ( x)dx
*
n
(13.4)
−∞
analoga alla (13.2) (si assume che le fn e la ψ siano normalizzate).
Il caso in cui lo spettro non è discreto è un po’ più complesso matematicamente e lo omettiamo, ma
il concetto base del calcolo della densità di probabilità resta lo stesso.
5.14 Dinamica quantistica: soluzione generale dell’equazione di Schroedinger
Ritorniamo ora al fatto che gli stati stazionari sono anche modi normali del sistema. Se scriviamo
una combinazione lineare di tutti gli stati stazionari, esplicitando adesso anche la loro dipendenza
dal tempo, tale combinazione lineare dovrebbe fornire la soluzione generale dell’equazione di
Schroedinger dipendente dal tempo, ossia la dinamica quantistica del sistema.
Consideriamo prima il caso di spettro di energie discreto, che è più semplice. Assumiamo quindi
che, come nell’esempio della buca di potenziale infinita, sia abbiano i seguenti
insieme delle energie possibili (caso discreto): E1, E2, ..., En, ....
e
insieme delle autofunzioni corrispondenti: φ1(x), φ2(x), ..., φn(x), ...
Gli stati stazionari veri e propri, completi della loro dipendenza temporale, si ottengono
moltiplicando le autofunzioni φn(x) per gli esponenziali che forniscono la dipendenza dal tempo,
come indicato nella (10.3), ossia:
insieme degli stati stazionari (caso discreto): ψ n ( x, t ) = φn ( x)e − iEnt /
(14.1)
La soluzione generale dell’equazione di Schroedinger dipendente dal tempo sarà allora la seguente
combinazione lineare di tutti gli stati stazionari:
∞
∞
n =1
n =1
soluzione generale eq. Schr. (spettro discreto): ψ ( x, t ) = ∑ cnψ n ( x, t ) = ∑ cnφn ( x)e − iEnt / (14.2)
Questa espressione descrive qualsiasi dinamica possibile della funzione d’onda, al variare dei
coefficienti cn. Notate che la (14.2) ha un significato diverso e più “forte” della (8.7) o (13.1),
perché la dipendenza dal tempo dei coefficienti è esplicita. In altre parole, in base a quanto detto in
precedenza potevamo già scrivere la (8.7) o (13.1) per ciascun istante di tempo t, ma non potevamo
conoscere la dipendenza dei coefficienti dal tempo, ossia le funzioni cn(t). La (14.2) fissa proprio
questa specifica dipendenza dal tempo. E’ importante anche notare che mentre lo sviluppo (8.7) si
può fare per qualsiasi osservabile O, l’espressione (14.2) è valida solo se le autofunzioni φn sono
proprio quelle dell’energia, ossia si riferiscono a stati stazionari.
In particolare, i coefficienti cn sono legati allo stato quantistico iniziale ψ(x) = ψ(x, 0). Ponendo
infatti t = 0 nella (14.2), si ottiene nuovamente un’espressione dello stato quantistico iniziale
44
analoga alla (13.1) o alla (8.7) che ci permette anche di trovare i coefficienti cn a partire dallo stato
iniziale mediante il prodotto scalare, come stabilito dalla (8.9).
Riepilogando, se si conosce lo stato quantistico iniziale ψ(x, 0) e si vuole determinare quello
successivo ψ(x,t) si può procedere secondo i seguenti due passi: (i) usando la (8.9) si calcolano i
coefficienti cn dello sviluppo (8.7) della funzione d’onda iniziale; (ii) si scrive la combinazione
“completa” (14.2) inserendo “vicino” a ciascun coefficiente il giusto esponenziale complesso che ne
descrive la dipendenza dal tempo.
Consideriamo ora il caso di spettro continuo, usando come esempio di riferimento la particella
libera e mettendo in evidenza l’analogia con quanto detto nel caso dello spettro discreto. Quando lo
spettro è continuo, si deve utilizzare una variabile continua per descrivere l’insieme di tutte le
autofunzioni, al posto dell’indice discreto n. Prendendo come esempio la particella libera, vediamo
che una possibile variabile continua appropriata è il numero d’onde k (ma anche la quantità di moto
p = ħk). In funzione di k, il valore dell’energia è dato dalla legge di dispersione
autovalori dell’energia nella particella libera: E (k ) =
k2
2m
2
(14.3)
(questa è l’equivalente dell’espressione delle En) ottenuta invertendo la (11.8), oppure dalle
relazioni equivalenti (1.5) o (1.6). La corrispondente autofunzione è data da una delle (11.9).
Utilizzando valori sia positivi che negativi di k (ossia includendo nel segno di k il verso della
propagazione, cioè utilizzando in effetti k = kx), queste due espressioni possono essere scritte con
una sola formula, ossia:
autofunzioni dell’energia nella particella libera: φk ( x) = Aeikx
(14.4)
(questa è l’equivalente dell’espressione delle φn) Gli stati stazionari completi della dipendenza dal
tempo si ottengono utilizzando la (10.3), ossia moltiplicando per l’esponenziale immaginario
exp(−iEt/ħ)=exp(−iωt):
stati stazionari nella particella libera (onde armoniche): ψ k ( x, t ) = Aeikx −iE ( k )t / = Aeikx −iω ( k ) t (14.5)
(che rappresenta l’equivalente dell’espressione delle ψn data dalla (14.1)). A questo punto, la
soluzione generale si ottiene facendo una combinazione lineare di tutte le ψk, ossia:
sol. generale eq. Schr. (caso continuo, 1D): ψ ( x, t ) =
∞
∞
−∞
−∞
∫ ckψ k ( x, t )dk =
∫ c ( k )e
ikx − iE ( k ) t /
dk (14.6)
che è l’equivalente della (14.2). Questa espressione è del tutto equivalente a quella già scritta per il
pacchetto d’onde della particella libera (2.1).
5.15 Relazione di indeterminazione energia-tempo
Quando una particella ha un’energia ben definita, ossia ΔE = 0, abbiamo visto che la sua dinamica è
quella di uno stato stazionario, il che implica che la distribuzione di probabilità per le misure di
posizione (o di altri osservabili) è costante nel tempo. Per avere una distribuzione di probabilità non
costante, ossia che varia nel tempo, è necessario avere a che fare con una “sovrapposizione” di stati
45
stazionari diversi, ossia una combinazione lineare come quella data dalla (14.2) o dalla (14.6).
Questo implica che per avere una dinamica quantistica con un tempo caratteristico Δt finito è
necessario avere una certa indeterminazione di energia ΔE diversa da zero.
In realtà, le leggi della meccanica quantistica implicano la possibilità di definire una vera e propria
relazione di indeterminazione riguardante le grandezze energia e tempo, ossia la seguente
relazione di indeterminazione energia-tempo:
ΔE Δt ≥
2
(15.1)
L’indeterminazione ΔE dell’energia in questa relazione è definita proprio come scarto quadratico
medio della variabile casuale energia nello stato quantistico considerato. L’indeterminazione
temporale Δt ha invece un duplice significato. Da un lato, il tempo Δt è un tempo caratteristico per
la variazione dello stato quantistico. Dall’altro, Δt fornisce anche una stima della variabilità
statistica delle misure del tempo in cui si verifica una condizione sperimentale prestabilita,
sensibile alla dinamica (ad esempio dell’istante di tempo in cui la particella viene misurata in una
regione prestabilita di posizioni).
Per capire il significato fisico della (15.1), conviene considerare un paio di esempi specifici. Una
particella libera 1D che si trova in uno stato quantistico ψ(x) descritto da un pacchetto d’onde, di
quantità di moto media p0 = ħk0 e di indeterminazione Δp = ħΔk. La velocità di gruppo associata a
tale pacchetto d’onde è vg = p0/m. La larghezza del pacchetto è data da Δx, che consideriamo
approssimativamente costante in quanto abbastanza grande.
Ora un pacchetto d’onde di larghezza Δx che si muove a velocità media vg si sposta di una
lunghezza uguale alla propria larghezza in un tempo caratteristico Δt = Δx/vg. Questo tempo Δt
rappresenta anche una indeterminazione nella variabile tempo t, nel senso che precisiamo ora.
Immaginiamo di porre un rivelatore della particella lungo l’asse x, e di registrare il tempo t in cui la
particella nel pacchetto passa “attraverso” il rivelatore. Questo tempo t è una variabile casuale,
perché dato che la particella si trova in un punto imprecisato del pacchetto di estensione Δx, anche il
tempo t per il quale la particella arriva sul rivelatore è imprevedibile, entro un intervallo che è
proprio dell’ordine di Δt = Δx/vg. Se Δx ha il significato statistico preciso di scarto quadratico medio
della posizione nel pacchetto, anche Δt avrà il significato statistico di scarto quadratico medio sulle
misure di tempo.
Ora, dato che la particella non possiede una quantità di moto p ben definita (entro l’intervallo Δp),
anche l’energia cinetica E = p2/(2m), non può essere ben definita, ossia possiede una
indeterminazione ΔE. Se Δp è piccolo, questa indeterminazione su E può essere ottenuta con la
normale tecnica della propagazione degli errori (in questo caso si tratta di indeterminazioni non
associate agli errori sperimentali, ma il metodo di propagazione è lo stesso):
indeterminazione sull’energia cinetica: ΔE =
∂E
∂p
Δp =
p = p0
p0
Δp = v g Δp
m
(15.2)
Moltiplicando ΔE per Δt = Δx/vg otteniamo ΔE Δt = Δp Δx, da cui si ottiene la (15.1).
Come secondo esempio, consideriamo una buca di potenziale infinita e una funzione d’onda ψ(x,t)
data dalla combinazione lineare di due stati stazionari qualsiasi ψn e ψm, ossia si ha
46
ψ ( x, t ) = cnψ n ( x, t ) + cmψ m ( x, t ) = cnφm ( x)e −iE t / + cmφm ( x)e−iE t /
n
m
(15.3)
La distribuzione di probabilità per la posizione della particella sarà allora data da
ψ ( x, t ) = cnφn ( x) + cmφm ( x) + 2 Re ⎡⎣cn cm∗ φn ( x)φm∗ ( x)e −i( E − E
2
2
2
n
m
)t /
⎤
⎦
(15.4)
E’ facile vedere che la dipendenza dal tempo di questa distribuzione di probabilità oscilla in modo
armonico, con una frequenza caratteristica di oscillazione corrispondente alla frequenza di Bohr per
la transizione tra i livelli En ed Em, ossia si ha la
frequenza caratteristica di una sovrapposizione di due stati stazionari: ωnm =
En − Em
(15.5)
Se ora definiamo il tempo caratteristico Δt come l’inverso di questa frequenza angolare e
l’indeterminazione nell’energia ΔE come il valore assoluto della differenza di energia tra i due
livelli, ΔE = |En − Em|, si ottiene ΔEΔt = ħ, che corrisponde ad un caso particolare della (15.1)
(anche se in questo esempio le indeterminazioni non hanno il significato statistico preciso di scarto
quadratico medio).
Se la particella nella buca di potenziale possiede una carica elettrica (ad esempio è un elettrone),
allora la distribuzione di probabilità per la posizione della particella corrisponde ad una
distribuzione media di carica elettrica. Ma secondo la normale teoria elettromagnetica, oscillazioni
armoniche nella distribuzione della carica elettrica di frequenza ωnm, daranno luogo
all’assorbimento e all’emissione di radiazione elettromagnetica alla medesima frequenza. Infatti, la
frequenza (15.5) corrisponde proprio alla frequenza (angolare) per l’emissione e l’assorbimento di
un fotone secondo le leggi di Bohr. In un certo senso, questo risultato quindi spiega il fatto che
l’emissione o l’assorbimento di radiazione elettromagnetica avviene proprio alle frequenze di Bohr.
Al di là di questi esempi specifici, si può dimostrare (ma omettiamo la dimostrazione) che la
relazione di indeterminazione (15.1) tra energia e tempo vale del tutto in generale. Notate che la
(15.1) implica che se un sistema possiede un’energia ben precisa, con indeterminazione nulla ΔE =
0, allora il tempo caratteristico Δt diverge, per cui la distribuzione di probabilità dovrebbe rimanere
costante nel tempo. Questo caso limite corrisponde infatti agli stati stazionari, la cui distribuzione
di probabilità non cambia nel tempo, per cui si può porre Δt = ∞.
Passiamo ora a studiare una serie di esempi particolari di sistemi fisici costituiti da una particella
che si muove in una energia potenziale U(x) assegnata, scelti in modo da poter essere risolti
analiticamente.
5.16 Il gradino di potenziale: onde evanescenti, trasmissione e riflessione
Consideriamo ora una particella che si muove in un’energia potenziale “a gradino”, ossia che
assume due valori costanti diversi in due regioni di spazio adiacenti, con un “salto” brusco tra i due
valori (cioè una “discontinuità”), come ad esempio nella figura seguente.
U(x)
U0
x
47
Per comodità, localizziamo l’origine dell’asse x in corrispondenza del gradino, e consideriamo nullo
il valore dell’energia potenziale per x negativi. L’energia potenziale U(x) è quindi
complessivamente data dalla seguente espressione:
⎧0
U ( x) = ⎨
⎩U 0
per
per
x≤0
(16.1)
x>0
dove U0 è un valore costante qualsiasi (che assumiamo positivo). Va notato che abbiamo posto U(x)
= 0 anche per il punto di confine x = 0, ma in realtà si poteva anche porre U(0) = U0 oppure un altro
valore ancora (purché finito) e la fisica non sarebbe stata diversa.
Questo gradino di potenziale è il primo esempio di un sistema con energia potenziale costante a
tratti, una classe di sistemi che possono essere risolti analiticamente. In questo tipo di problemi, si
può procedere con i seguenti passi: (1) per un dato valore di E, si risolve l’equazione di
Schroedinger separatamente in ciascuna regione in cui U(x) è costante, eliminando le soluzioni che
non sono fisicamente valide; (2) si “collegano” tra loro le soluzioni trovate con le condizioni di
raccordo (10.7).
Applichiamo il metodo delineato al caso specifico del gradino di energia potenziale. Consideriamo
prima separatamente le due regioni x < 0 (regione I) e x > 0 (regione II). Sostituendo la (16.1)
nell’equazione di Schroedinger (10.4), otteniamo in ambedue i casi un problema analogo a quello
trattato nel paragrafo 11. Nella regione I abbiamo proprio i risultati visti nel paragrafo 11, mentre
nella regione II dobbiamo tenere conto della presenza dell’energia costante U0, per cui i risultati
sono ancora gli stessi a patto di sostituire E−U0 al posto di E. Va sottolineato che l’energia E della
particella è la stessa in ambedue le regioni, perché l’equazione di Schroedinger da cui si parte è
un’unica equazione che contiene un solo autovalore E (il che corrisponde anche fisicamente al fatto
che l’energia totale della particella si conserva durante il suo moto).
Nel fare la nostra analisi dobbiamo considerare ancora una volta diversi casi a seconda del valore
dell’energia E della particella. In particolare dobbiamo distinguere i tre casi seguenti: E < 0; 0 ≤ E <
U0; E ≥ U0 (i punti di confine tra i casi elencati, come ad esempio E = U0, possono essere trattati
come limite dei casi adiacenti).
Prima di tutto consideriamo brevemente il caso E < 0. Risolvendo il problema nella sua interezza, è
possibile dimostrare che in questo caso non esistono soluzioni fisicamente valide, anche se la
dimostrazione è meno ovvia di quel che potremmo credere, per il motivo che capiremo più avanti.
In ogni caso, è chiaro che la particella non può avere in tutto lo spazio un’energia totale minore
dell’energia potenziale, perché questa corrisponderebbe ad un’energia cinetica sempre negativa, il
che non ha significato fisico.
Consideriamo ora il caso in cui 0 < E < U0. Come abbiamo detto possiamo semplicemente
riprendere le soluzioni del paragrafo 11. Nella regione I otteniamo le soluzioni (11.9) con k dato
ancora dalla (11.8). In generale la funzione d’onda sarà la combinazione lineare delle due soluzioni,
per cui sarà:
soluzione nella regione I:
φ ( x) = Aeikx + Be− ikx (x < 0)
(16.2)
48
Nella regione II, essendo E < U0, otteniamo invece le soluzioni esponenziali reali del tipo φ = A e±χx,
con χ dato dalla (11.4) dopo la sostituzione di E con E−U0, cioè
χ=
2m(U 0 − E )
2
(16.3)
Ora nel paragrafo 11 avevamo scartato entrambe queste soluzioni perché divergono per x→±∞. Ma
ora queste soluzioni si riferiscono solo alla regione con x > 0, per cui il limite x→−∞ non ha più
significato perché esce dalla regione in cui la soluzione si applica. Perciò adesso scartiamo in
quanto non fisicamente valida solo la soluzione con andamento e+χx, mentre l’altra soluzione, con
andamento e−χx, dobbiamo conservarla.
In altre parole, al contrario di quanto avveniva nel paragrafo precedente, nella regione II per energie
E < U0, ossia minori dell’energia potenziale, abbiamo ora la seguente nuova soluzione esponenziale,
detta anche
onda evanescente (soluzione regione II):
φ ( x) = Ce − χ x
(x > 0) (16.4)
dove C è un’ampiezza indeterminata e χ è dato dalla (16.3). L’andamento esponenziale decrescente
della funzione d’onda evanescente è illustrato nella figura seguente (il grafico si riferisce solo alla
regione II, ossia x > 0).
φ(x)
x
L’esistenza di soluzioni come questa nella regione II è fisicamente molto interessante, in quanto
corrisponde alla possibilità (con probabilità non nulla) di ritrovare la particella in una regione di
spazio in cui l’energia totale E è minore dell’energia potenziale U. Questa regione sarebbe invece
classicamente inaccessibile (o proibita), perché corrisponderebbe ad una energia cinetica negativa.
Quindi la meccanica quantistica prevede la possibilità per la particella di penetrare regioni
inaccessibili secondo la fisica classica. La lunghezza caratteristica di penetrazione è data dalla
costante di decadimento esponenziale della densità di probabilità dP/dx = |φ|2(x) associata all’onda
evanescente, ossia
lunghezza caratteristica di penetrazione dell’onda evanescente:
l≈
1
=
2χ
8m (U 0 − E )
(16.5)
Ora applichiamo le condizioni di raccordo (10.7) alle soluzioni (16.2) e (16.4). Otteniamo così le
seguenti equazioni:
A+ B = C
ik ( A − B) = − χ C
(16.6)
Queste due equazioni ci permettono di determinare due delle tre ampiezze A, B e C che abbiamo
introdotto. Ad esempio, possiamo determinare B e C in termini di A, ottenendo:
49
ik + χ
A
ik − χ
(16.7)
2ik
C=
A
ik − χ
B=
Riassumendo i risultati ottenuti, la funzione d’onda dello stato stazionario con energia E compresa
tra 0 e U0 è data dalla seguente espressione:
⎧ Aeikx + Be − ikx
φ ( x) = ⎨
⎩
Ce
−χx
per
x≤0
per
x≥0
(16.8)
con k data dalla (11.8), χ data dalla (16.3) e le costanti B e C date dalle (16.7). Tutte queste costanti
dipendono dall’energia E. Va notato che se c’è un’onda armonica nella regione I che viaggia in
avanti (onda incidente sul gradino), le relazioni (16.7) implicano che debba esserci necessariamente
anche un’onda riflessa dal gradino e un’onda evanescente al di là del gradino (che non è un’onda
“trasmessa”, perché si annulla per x→∞). L’ampiezza dell’onda riflessa è in modulo uguale a quella
dell’onda incidente, cioè si ha |B|=|A|, come si può facilmente verificare a partire dalla prima delle
(16.7). La sovrapposizione dell’onda incidente e dell’onda riflessa nella regione I assume la forma
di un’onda armonica stazionaria.
L’intera soluzione (16.8) è rappresentata graficamente nella figura seguente, dove è disegnata a fini
illustrativi solo la parte reale della φ(x) (che in generale è complessa). La parte immaginaria ha un
andamento del tutto simile.
Re[φ(x)]
x
Il significato fisico di queste soluzioni sarà comunque ulteriormente chiarito più avanti, quando
analizzeremo la dinamica di un pacchetto d’onde costruito mediante una loro combinazione lineare.
Osservando la soluzione trovata, ci si potrebbe chiedere come mai una costante, la A, resta
comunque indeterminata. La risposta è che la funzione d’onda ψ è sempre definita a meno di una
costante moltiplicativa, la quale viene fissata dalla condizione di normalizzazione, quando la ψ è
normalizzabile. Altrimenti, la costante resta indeterminata.
Notiamo infine che abbiamo determinato una sola funzione d’onda indipendente per ciascun valore
dell’energia E, per cui nell’intervallo di energie (0,U0), lo spettro di energie è continuo e il grado di
degenerazione è uno.
50
Torniamo ora per un momento al caso E < 0. Ci rendiamo conto ora che il motivo per cui non
abbiamo escluso l’onda evanescente nella regione II continua ad essere valido anche per E < 0.
Inoltre, nella regione I per E < 0 ci può essere un’altra onda evanescente (decrescente nell’altro
verso, ossia del tipo Aeχx) che pure non viola la condizione di validità fisica, dato che in questa
regione non ha senso il limite x→∞. Tuttavia, applicando a queste due onde evanescenti le
condizioni di raccordo (10.7), scopriamo che le loro ampiezze devono necessariamente annullarsi,
cioè si ha φ(x) = 0 dappertutto. Questo è il motivo per cui per E < 0 non ci sono soluzioni (a parte
quella nulla, che non ha significato fisico).
Infine, affrontiamo il caso E > U0. Ora in entrambe le regioni avremo soluzioni del tipo onde
armoniche, cioè avremo la seguente soluzione:
⎧ Aeikx + Be − ikx
φ ( x) = ⎨ ik ′x
− ik ′x
⎩Ce + De
x≤0
x≥0
per
per
(16.9)
dove k è dato ancora dalla (11.8) e k′ è dato dalla seguente espressione:
k′ =
2m( E − U 0 )
2
= k2 −
U0
2
(16.10)
le quattro ampiezze A, B, C e D sono legate tra loro dalle seguenti relazioni, ottenute a partire dalle
condizioni di raccordo (10.7):
A+ B = C + D
k ( A − B ) = k ′ (C − D )
(16.11)
Possiamo liberamente fissare due delle quattro costanti e determinare le altre due. Di solito si
sceglie di fissare A e D, che rappresentano le ampiezze delle due onde incidenti sul gradino e
provenienti dalle due direzioni opposte. Dalle (16.11) otteniamo facilmente le altre due costanti,
ossia le ampiezze delle onde riflesse e trasmesse:
2k
k′ − k
A+
D
k + k′
k′ + k
(16.12)
k − k′
2k ′
B=
A+
D
k + k′
k′ + k
C=
Il fatto che ci siano due costanti libere corrisponde a dire che abbiamo individuato due funzioni
d’onda linearmente indipendenti (ad esempio quella che si ottiene ponendo D = 0 e quella che si
ottiene ponendo A = 0) per ciascun valore di energia E, cioè che per E > U0 lo spettro di energie è
continuo e il grado di degenerazione è due.
Le (16.12) descrivono i processi di trasmissione e riflessione delle onde armoniche sul gradino di
energia potenziale. Se ad esempio poniamo D = 0 e A ≠ 0, ossia consideriamo una soluzione in cui
c’è solo un’onda incidente da sinistra, allora l’onda di ampiezza B corrisponde all’onda riflessa sul
gradino e l’onda di ampiezza C corrisponde a quella trasmessa. Perciò i seguenti rapporti tra le
ampiezze definiscono i coefficienti di riflessione e trasmissione:
51
coefficiente di riflessione sul gradino: R =
B k − k′
=
A k + k′
coefficiente di trasmissione sul gradino: T =
(16.13)
C
2k
(16.14)
=
A k + k′
Per il caso in cui l’onda proviene dall’altra direzione (cioè A = 0 e D ≠ 0) si può notare che i
coefficienti sono dati dalle stesse espressioni salvo per lo scambio di k e k′. Un esempio di
soluzione è illustrato nella figura seguente, dove si vede che l’onda cambia di ampiezza e di
lunghezza d’onda in corrispondenza del gradino.
Re[φ(x)]
x
Abbiamo visto che i coefficienti di riflessione e trasmissione R e T ci forniscono l’ampiezza
dell’onda riflessa e dell’onda trasmessa in funzione dell’ampiezza A dell’onda incidente. Ma tali
onde sono armoniche, ed infinitamente estese. Perciò ragionando esclusivamente su tali onde non è
possibile calcolare la probabilità di un evento dinamico. Ad esempio, supponiamo che una particella
si trovi inizialmente nella regione I e stia viaggiando verso il gradino. Ad un certo punto la
particella interagirà con il gradino, e al termine dell’interazione, se effettuiamo una misura della
posizione della particella, la ritroveremo nella regione II oppure nella regione I con certe
probabilità. Si tratta cioè di calcolare la probabilità che una particella incidente sul gradino venga
riflessa o trasmessa, il primo e più semplice esempio di “collisione” quantistica.
Trattandosi di un processo dinamico, è necessario ricorrere ad una analisi basata sulle combinazioni
lineari di stati stazionari. Trattandosi di un caso di spettro continuo, è necessario utilizzare una
combinazione lineare analoga alla (14.6), ossia un integrale di pacchetto d’onde analogo al caso
della particella libera. Le funzioni d’onda φk(x) da inserire nell’integrale, però, non sono più le
semplici onde armoniche ma sono date ora dalle espressioni (16.8) oppure (16.9) a seconda del
valore dell’energia E rispetto all’altezza del gradino U0. Come “indice” k che scandisce l’insieme di
tutte le autofunzioni, possiamo utilizzare il numero d’onde nella regione x < 0 (infatti quello nella
regione x > 0, ossia k′, viene fissato da k mediante la relazione (16.10)), includendovi anche il segno
per specificare il verso di propagazione.
La soluzione generale sarà data da una combinazione lineare delle φk(x), che assume la forma di un
integrale nella variabile k. Anziché considerare la più generale combinazione lineare possibile,
facciamo qui solo l’esempio di un pacchetto d’onde con larghezza di banda Δk molto stretta centrata
intorno ad un numero d’onde k = k0, e costruito utilizzando solo onde incidenti provenienti da
sinistra (da x < 0) e con k tali che E > U0. L’equivalente della (14.6) è quindi la seguente
espressione:
52
ψ ( x, t ) = ∫ c(k )φk ( x)e
− iω ( k ) t
⎧ c(k ) ⎡ ei[kx −ω ( k ) t ] + R(k )e −i[ kx +ω ( k )t ] ⎤ dk
⎪∫
⎣
⎦
dk = ⎨
i[ k ′ ( k ) x −ω ( k ) t ]
dk
⎪⎩
∫ c(k )T (k )e
per
per
x<0
x>0
(16.15)
dove gli estremi di integrazione non servono perché stiamo assumendo che c(k) sia
significativamente diverso da zero solo in un intervallo piccolo, R(k) e T(k) sono i coefficienti di
riflessione e trasmissione definiti dalle (16.13) e (16.14), e la funzione k′(k) è definita dalla (16.10).
La (16.15) può ora essere calcolata in modo approssimato utilizzando l’espressione (2.3) per la
frequenza ω(k) e un analogo sviluppo in serie di Taylor troncata al primo ordine per la funzione
k′(k). Quest’ultimo fornisce
k ′(k ) ≈ k ′(k0 ) +
( dk ′ dω )k =k0
v
dk ′
( k − k0 ) = k0′ +
( k − k0 ) = k0′ + ′g ( k − k0 )
dk k = k0
vg
( dk dω )k =k
(16.16)
0
dove v′g = dω/dk′ = ħk′0/m è la velocità di gruppo dell’onda nella regione x > 0. Inoltre, i
coefficienti R(k) e T(k) possono essere sviluppati in serie di Taylor attorno a k = k0, troncando lo
sviluppo all’ordine zero, ossia ponendo:
R (k ) ≈ R(k0 ) = R0
T (k ) ≈ T (k0 ) = T0
(16.17)
Utilizzando tutte queste approssimazioni, la (16.15) può essere trasformata nella seguente
espressione:
⎧eiϕi (t )ψ 0 ( x − v g t ) + R0 eiϕR (t )ψ 0 ( x + v g t ) per x < 0
⎪
⎞
ψ ( x, t ) = ⎨ iϕT ( x ,t ) ⎛ v g
′
−
T
e
x
v
t
per x > 0
ψ
⎜
⎟
(
)
0
0
g
⎪
⎜ v′
⎟
⎝ g
⎠
⎩
(16.18)
dove ϕi, ϕR e ϕT sono fasi opportune e ψ0 corrisponde alla forma del pacchetto d’onde che si ha per
t = 0. La (16.18) può ora essere agevolmente interpretata fisicamente. Il primo termine relativo alla
regione x < 0 descrive un pacchetto d’onde che viaggia verso il gradino, ossia il pacchetto d’onde
incidente. Il termine in cui appare il fattore R0 corrisponde ad un pacchetto d’onde riflesso,
localizzato anche lui nella regione x < 0, ma viaggiante verso sinistra. Il termine in cui appare il
fattore T0 corrisponde infine ad un pacchetto d’onde trasmesso, in quanto viaggiante nella regione x
> 0 verso destra.
Se assumiamo che per t = 0 la funzione ψ0(x) sia diversa da zero solo nella regione x < 0, possiamo
vedere immediatamente che il pacchetto d’onde riflesso e trasmesso sono diversi da zero solo nelle
regioni dove le relative espressioni non si applicano (cioè il pacchetto riflesso risulterà diverso da
zero per x > 0 e quello trasmesso per x < 0), per cui fisicamente non esistono. Questo corrisponde al
fatto che per t = 0 la collisione con il gradino del pacchetto d’onde incidente ancora non è avvenuta.
Al trascorrere del tempo, il pacchetto incidente arriva sul gradino e vi “scompare dentro” (cioè la
formula ψ0(x−vgt) risulta non nulla solo per x > 0, dove non si applica). Allo stesso tempo appare il
53
pacchetto riflesso (perché entra nella regione x < 0) e quello trasmesso (perché entra nella regione x
> 0).
Ignorando i fattori di fase, notate che il pacchetto d’onde riflesso risulta avere la stessa forma di
quello incidente, salvo per l’ampiezza che risulta moltiplicata per il coefficiente di riflessione R0. Il
pacchetto trasmesso invece, oltre ad avere un’ampiezza moltiplicata per il fattore T0, ha la stessa
forma di quello incidente salvo per una variazione della scala dell’asse x per il fattore v′g/vg. In altre
parole, il pacchetto d’onde trasmesso risulta compresso nella sua estensione spaziale del medesimo
fattore v′g/vg = k′0/k0.
Tale compressione può essere facilmente spiegata fisicamente con il seguente argomento.
Immaginiamo il caso di un pacchetto d’onde incidente con un inviluppo di forma rettangolare di
estensione Δx. Il pacchetto trasmesso inizia ad essere generato a partire dal momento in cui il
pacchetto incidente inizia ad “entrare” nel gradino e solo fino al momento in cui tutto il pacchetto
incidente è entrato. Dato che il pacchetto incidente e quindi anche il suo inizio e la sua fine
viaggiano alla velocità di gruppo vg, il pacchetto d’onde trasmesso viene generato nel corso di un
intervallo temporale Δt = Δx/vg. Dato che inizio e fine del pacchetto d’onde trasmesso viaggiano
alla velocità di gruppo v′g, l’estensione del pacchetto trasmesso risulterà Δx′ = v′g Δt = (v′g/vg)Δx,
cioè il pacchetto d’onde trasmesso viene compresso (sul gradino si ha v′g < vg).
Ora che abbiamo studiato la dinamica dei pacchetti d’onde finiti, possiamo finalmente calcolare le
probabilità di trasmissione e riflessione sul gradino di una particella secondo le leggi della
meccanica quantistica.
Assumiamo che inizialmente la particella sia certamente “contenuta” in un pacchetto d’onde
incidente viaggiante verso il gradino nella regione I. Se A =|ψ0| è l’ampiezza del pacchetto d’onde
nella regione in cui esso non è nullo e Δx l’estensione del pacchetto, allora si ha la seguente
condizione di normalizzazione:
A2Δx = 1 (16.19)
Il pacchetto riflesso avrà invece ampiezza RA. L’integrale del modulo quadro dell’intero pacchetto
riflesso corrisponderà alla probabilità di trovare la particella nella regione x < 0 (all’interno del
pacchetto riflesso) dopo la collisione, ovvero alla
probabilità di riflessione sul gradino: PR = R0 A Δx = R0
2
2
2
⎛ k − k′ ⎞
=⎜ 0 0 ⎟
⎝ k0 + k0′ ⎠
2
(16.20)
dove abbiamo usato la (16.19) per eliminare il prodotto A2Δx. L’integrale del modulo quadro
dell’intero pacchetto trasmesso invece fornirà la probabilità di trovare la particella nella regione x >
0 (all’interno del pacchetto trasmesso) dopo la collisione, ovvero la
probabilità di trasmissione sul gradino: PT = T0 A2 Δx′ = T0 A2
2
2
v′g
vg
Δx =
k0′ 2
4k0 k0′
T0 =
2
k0
( k0 + k0′ )
(16.21)
dove abbiamo anche sfruttato il fatto che vg = ħk0/m e v′g = ħk′0/m.
E’ facile verificare che PR + PT = 1, come deve essere.
54
5.17 Particella in buca di potenziale rettangolare finita
Una “buca di potenziale rettangolare finita” è un sistema con la seguente energia potenziale:
⎧ 0
⎪
U ( x) = ⎨−U 0
⎪ 0
⎩
x<0
per
per 0 ≤ x ≤ L
x>L
per
(17.1)
Sappiamo che l’energia potenziale è definita a meno di una costante additiva qualsiasi. In questo
caso abbiamo sfruttato questa libertà per porre uguale a zero l’energia potenziale all’infinito, come
si usa quando è possibile (ovviamente non era possibile nella buca infinita).
Questo problema si affronta in modo del tutto analogo ai precedenti. Per E ≤ −U0 si dimostra che
non si hanno soluzioni dell’equazione di Schroedinger che soddisfino alla condizione di validità
fisica. Per −U0 < E < 0 le soluzioni esistono e sono date dalla seguente espressione:
⎧
Ae χ x
⎪
φ ( x) = ⎨ Beikx + Ce− ikx
⎪ De − χ x
⎩
per
x≤0
per 0 ≤ x ≤ L
x≥L
per
(17.2)
con
χ=
2m( − E )
2
(17.3)
e
k=
2m ( E + U 0 )
2
(17.4)
Le quattro condizioni di raccordo che si ottengono per x = 0 e x = L legano tra loro i coefficienti A,
B, C e D che appaiono nella (17.2). Si potrebbe pensare che queste quattro equazioni determinino il
valore di tutte e quattro le costanti, ma non è così (se così fosse, trattandosi di un sistema di 4
equazioni lineari in 4 incognite la soluzione sarebbe unica; dato che una soluzione valida è che tutte
le costanti si annullino, sarebbe questa l’unica soluzione, che però corrisponde ad una funzione
d’onda nulla). L’unico modo perché vi siano soluzioni non nulle in cui solo tre costanti sono
determinate e la quarta resta libera di assumere qualsiasi valore è che l’energia soddisfi una
condizione aggiuntiva che rende le quattro equazioni non linearmente indipendenti (confrontate
questo fatto con quello che succede con la buca infinita). Non è difficile, anche se è un po’
laborioso, dimostrare che la condizione sull’energia è la seguente:
E + U0
⎛π L
= tan ⎜ −
−E
⎝2 2
⎞
2m ( E + U 0 ) ⎟ oppure
⎠
E + U0
⎛ L
= tan ⎜ −
−E
⎝ 2
⎞
2m ( E + U 0 ) ⎟ (17.5)
⎠
(cioè l’energia è valida se una delle due equazioni è soddisfatta).
55
Queste sono due equazioni trascendenti, e non possono essere risolte analiticamente. Tuttavia è
facile risolverle numericamente e ammettono un insieme discreto e finito di soluzioni E1, E2,... ecc.,
cioè uno spettro discreto di energia. Uno studio grafico delle soluzioni della (17.5) ci permette di
trovare la seguente utile espressione per le energie dello spettro discreto:
energie della buca di potenziale finita: En = −U 0 +
π2
2
2mL
2
(n − εn )
2
con n = 1, 2,..., N (17.6)
dove i numeri εn sono tutti compresi tra 0 e 1 e N rappresenta il numero di livelli discreti possibili
dell’energia. La (17.6) mostra che l’energia, misurata a partire dal fondo della buca −U0, ha un
andamento identico a quello della buca infinita, salvo per la sostituzione dei numeri quantici n con
dei numeri “corretti” n−εn, che sono comunque compresi tra n−1 ed n. Perciò ogni livello energetico
En della buca finita soddisfa alla relazione E′n−1 <En <E′n dove E′n sono i livelli di una buca di
potenziale di uguale larghezza L e di uguale valore del potenziale del “fondo” −U0 ma con pareti
“infinite”. Il numero N di stati localizzati si può determinare con la seguente procedura: N è uguale
al primo numero quantico n per il quale l’energia calcolata con la (11.4) supererebbe il valore 0
(cioè entrerebbe nello spettro continuo) se la “correzione” εn si annullasse (ossia per il quale
l’energia misurata dal fondo della buca E+U0 e calcolata con la formula della buca infinita supera
l’altezza della buca). Ovviamente, l’energia EN è in realtà sempre minore di zero, grazie alla
presenza della correzione. Notate che con questo criterio concludiamo che almeno una soluzione c’è
sempre, ossia N ≥ 1, anche per buche di potenziale molto poco profonde.
Infine, per E > 0 è facile dimostrare che tutti i valori di energia sono ammessi, ciascuno con grado
di degenerazione due (ossia ci sono due soluzioni indipendenti). Perciò E > 0 è una regione di
spettro continuo di energia. Ne concludiamo che la buca di potenziale finita ha uno spettro di
energie “misto”, discreto (e finito) per energie negative e continuo per energie positive.
Questa suddivisione dello spettro energetico in una regione di spettro discreto (non sempre finito)
ed una di spettro continuo non è specifico della buca di potenziale “rettangolare” considerata qui,
ma è del tutto generale. Il confine tra le due regioni è fissato dal valore dell’energia potenziale
all’infinito (il valore più basso, se i due limiti per x →±∞ hanno diverso potenziale). Notate che la
regione con energie negative corrisponde anche al caso in cui la particella è “legata”, ossia non può
sfuggire alla buca di potenziale perché non ha abbastanza energia. Invece la regione con energie
positive è quella in cui la particella, pur interagendo con la buca di potenziale, resta libera. Infine,
va notato che le autofunzioni associate allo spettro discreto sono sempre normalizzabili, mentre
quelle relative allo spettro continuo non lo sono mai. Queste caratteristiche generali di sistemi con
spettro misto sono illustrate nella figura seguente.
E, U(x)
Spettro continuo
(stati
non legati e autofunzioni non
normalizzabili)
Spettro discreto
(stati legati
e autofunzioni normalizzabili)
56
5.18 Barriera di potenziale rettangolare: effetto tunnel
Come ultimo esempio di sistema con energia potenziale costante a tratti, consideriamo un sistema in
cui c’è una barriera di potenziale rettangolare (l’opposto della buca di potenziale rettangolare), cioè
in cui l’energia potenziale è la seguente:
⎧0
⎪
U ( x) = ⎨U 0
⎪0
⎩
per
x<0
per 0 ≤ x ≤ L (18.1)
x>L
per
Ci concentriamo solo sul caso E < U0, dove classicamente una particella incidente da un lato
qualsiasi della barriera non può penetrarla e pertanto viene sempre riflessa. Assumendo che vi sia
solo l’onda incidente proveniente da sinistra, l’equazione di Schroedinger indipendente dal tempo
per questo caso fornisce la seguente soluzione:
⎧ Aeikx + Be− ikx
⎪
φ ( x) = ⎨Ce − χ x + De χ x
⎪
Eeikx
⎩
per
x≤0
per 0 ≤ x ≤ L
per
x≥L
(18.2)
dove k è dato dalla (11.8) e χ dalla (16.3).
Imponendo le quattro condizioni di raccordo si determinano tutte le ampiezze in funzione, ad
esempio, di quella dell’onda incidente A. In particolare risolvendo queste equazioni è possibile
calcolare il coefficiente di trasmissione T della barriera, definito come il rapporto tra l’ampiezza E
dell’onda armonica presente oltre la barriera e l’ampiezza A dell’onda incidente:
T=
E
2ik χ e − ikL e − χ L
=
A ( χ + ik )2 e −2 χ L + ( χ − ik )2
(18.3)
L’esistenza di un’onda trasmessa, come vedremo meglio più avanti, corrisponde ad una probabilità
finita che la particella, provenendo da sinistra, attraversi la barriera. Tale possibilità è invece esclusa
dalla fisica classica. L’attraversamento di una barriera di energia potenziale più alta dell’energia
totale della particella è quindi un fenomeno specificamente quantistico. Dato che la particella
attraversa la barriera senza poterla scavalcare, il fenomeno descritto è detto effetto tunnel. Esso si
può verificare con qualsiasi barriera di energia potenziale, anche non rettangolare, la cui altezza sia
maggiore dell’energia della particella.
E’ abbastanza ovvio che l’effetto tunnel è strettamente legato all’esistenza delle onde evanescenti
all’interno della barriera. Una tipica funzione d’onda ottenuta dopo aver imposto le condizioni di
raccordo nella (18.2) è illustrata nella figura seguente.
Re[φ(x)]
x
57
5.19 Oscillatore armonico quantistico
Consideriamo ora il primo esempio di un sistema con energia potenziale che non è costante a tratti,
ma che è comunque possibile risolvere in modo analitico. Si tratta del cosiddetto “oscillatore
armonico quantistico”, ossia di un sistema in cui la particella è soggetta ad una forza di richiamo
proporzionale allo spostamento, come quella di una molla. L’energia potenziale è in questo caso
quadratica nello spostamento, ossia può essere scritta nel modo seguente:
energia potenziale per oscillatore armonico:
U ( x) =
1
ke x 2 (19.1)
2
dove ke è la “costante elastica” e abbiamo posto uguale a zero l’energia potenziale nell’origine
(come per la buca rettangolare infinita, non è possibile azzerare l’energia potenziale all’infinito, in
quanto diverge). L’oscillatore armonico è quindi una buca di potenziale di altezza infinita, ma di
forma arrotondata anziché rettangolare. L’importanza di questo problema è accresciuta dal fatto, già
menzionato nel primo capitolo, che qualsiasi energia potenziale che presenti un minimo
sufficientemente regolare può essere approssimata, per piccoli spostamenti x, da un’espressione
quadratica come la (19.1). Ad esempio molte vibrazioni degli atomi all’interno di molecole o
cristalli sono approssimativamente armoniche e la loro dinamica quantistica è in prima
approssimazione quella di un oscillatore armonico quantistico ideale.
L’equazione di Schroedinger indipendente dal tempo assume ora la forma seguente:
−
d 2φ 1
+ ke x 2φ = Eφ
2
2m dx
2
2
(19.2)
Questa equazione non è a coefficienti costanti (neanche per regioni limitate), per cui gli
esponenziali non sono soluzioni (come si può verificare sostituendovi la soluzione di prova (11.2)).
La presenza di un termine in x2 per la funzione e di una derivata seconda della stessa funzione
suggerisce che una funzione di tipo “gaussiano”, ossia esponenziale di x2, possa funzionare.
Tentiamo quindi la seguente soluzione di prova:
φ ( x) = Ae−α x
2
/2
(19.3)
dove α è una costante da determinare e il fattore −1/2 è stato inserito solo per convenienza di
notazione nei calcoli successivi. Sostituendo la (19.3) nella (19.2) e svolgendo i calcoli, vediamo
che effettivamente l’equazione è risolta se scegliamo opportunamente il valore di α per far
annullare tutti i termini in x2exp(−αx2/2), ma a condizione che l’energia E assuma un valore ben
preciso per far uguagliare i termini residui. In particolare, introducendo la frequenza angolare
ω = ke m definita come la frequenza angolare che avrebbe l’oscillatore classicamente, abbiamo
α=
mω
(19.4)
58
e
E = E0 =
1
ω
2
(19.5)
E’ chiaro che abbiamo avuto fortuna, e abbiamo individuato un particolare stato quantistico
stazionario, di energia E = E0 data dalla (19.5), ma che ce ne possono essere altri. Come facciamo a
trovarli?
Uno studio completo (che omettiamo) dell’equazione (19.2) mostra che le altre soluzioni si
ottengono moltiplicando la soluzione già trovata (19.3) per opportuni polinomi H(x). I polinomi che
moltiplicati per la (19.3) forniscono tutte le soluzioni della (19.2) sono noti come polinomi di
Hermite e sono indicati solitamente con Hn(x′), dove x′ = x α è una variabile posizione
adimensionale e n = 0, 1, 2, ... sono tutti i numeri interi non negativi (cioè è incluso lo zero). I primi
cinque polinomi di Hermite sono i seguenti:
H0 = 1
H1 = 2x′
H2 = 4x′2−2
H3 = 8x′3−12x′
H4 = 16x′4−48x′2+12
(19.6)
Quindi le soluzioni complete della (19.2) sono le seguenti:
(
)
autofunzioni dell’oscillatore armonico: φn ( x) = An H n x α e −α x
2
/2
(19.7)
dove An sono opportune costanti di normalizzazione. Infatti le soluzioni (19.7) sono tutte
normalizzabili. Alle autofunzioni (19.7) corrispondono le seguenti energie:
livelli di energia per l’oscillatore armonico:
1⎞
⎛
En = ⎜ n + ⎟ ω
2⎠
⎝
n = 0, 1, 2, ... (19.8)
Notate che l’oscillatore armonico, come in tutti i casi di particella confinata, possiede uno spettro di
energie discreto. La minima energia, ossia l’energia di punto zero E0 = ħω/2, è maggiore di zero.
Queste caratteristiche sono simili al caso della buca di potenziale rettangolare infinita. Tuttavia,
l’oscillatore armonico ha anche la caratteristica peculiare che i suoi livelli di energia sono
equispaziati, con intervalli tra livelli consecutivi pari a ħω. In questo differisce dalla buca
rettangolare.
59