2009-10 Prof. G. Galeotti – Materiali
2. LA SOLUZIONE DEL PROBLEMA DI LEANDRO
L'EQUILIBRIO DI LEANDRO:
Parallela a CT,
tangente ai RT
B
RT, CT
RT, CT
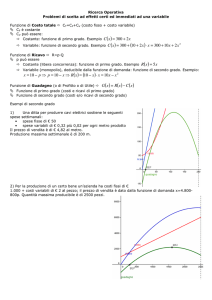
5. La scheda 1 è il punto di partenza per mostrare come l'e- Ricavi
soluzione grafica
Costi
quilibrio di Leandro si possa individuare graficamente in
H
HF: domanda = ricavi medi
tre passaggi, come mostra la fig.10:
(i) partendo dalla domanda di melograni (HF) dei clienti,
E HL: ricavi marginali
B
(ii) ricavando da quella domanda i ricavi marginali HL,
rendita di
(iii) eguagliando questi ultimi ai costi marginali OC (eLeandro
OC: costi costanti
guali ai costi medi supposti costanti per semplicità).
(costi medi =
C
D
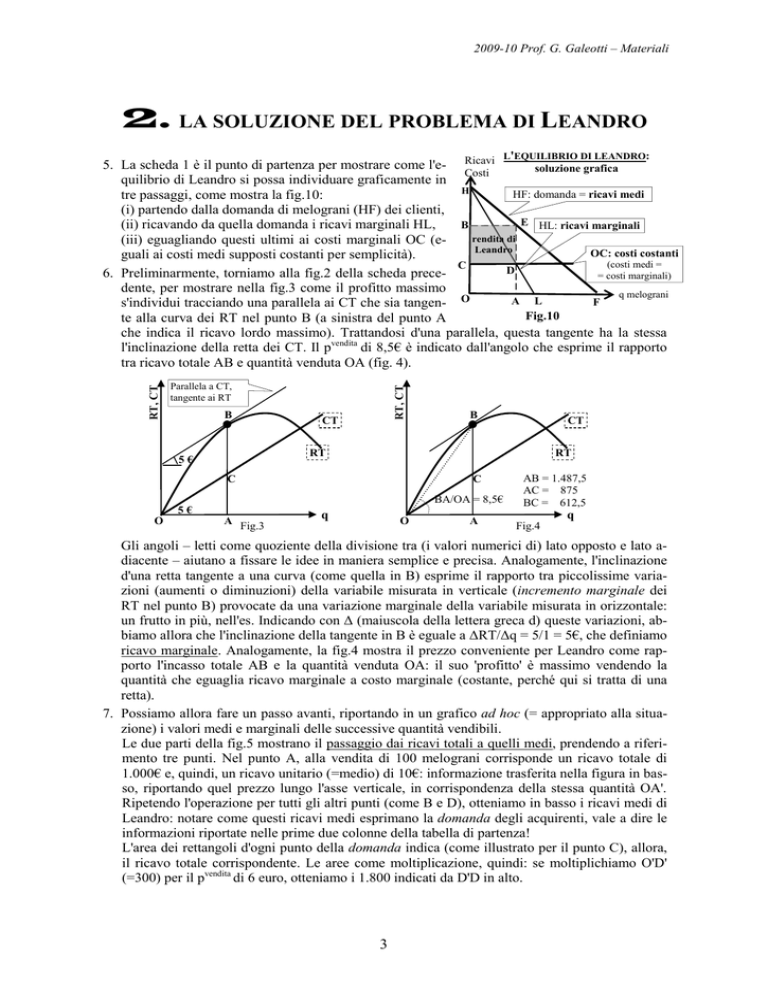
6. Preliminarmente, torniamo alla fig.2 della scheda prece= costi marginali)
dente, per mostrare nella fig.3 come il profitto massimo
q melograni
A L
F
s'individui tracciando una parallela ai CT che sia tangen- O
Fig.10
te alla curva dei RT nel punto B (a sinistra del punto A
che indica il ricavo lordo massimo). Trattandosi d'una parallela, questa tangente ha la stessa
l'inclinazione della retta dei CT. Il pvendita di 8,5€ è indicato dall'angolo che esprime il rapporto
tra ricavo totale AB e quantità venduta OA (fig. 4).
CT
CT
RT
5€
RT
C
C
BA/OA = 8,5€
5€
O
B
A
q
O
(=175)
Fig.3
A
AB = 1.487,5
AC = 875
BC = 612,5
q
Fig.4
Gli angoli – letti come quoziente della divisione tra (i valori numerici di) lato opposto e lato adiacente – aiutano a fissare le idee in maniera semplice e precisa. Analogamente, l'inclinazione
d'una retta tangente a una curva (come quella in B) esprime il rapporto tra piccolissime variazioni (aumenti o diminuzioni) della variabile misurata in verticale (incremento marginale dei
RT nel punto B) provocate da una variazione marginale della variabile misurata in orizzontale:
un frutto in più, nell'es. Indicando con Δ (maiuscola della lettera greca d) queste variazioni, abbiamo allora che l'inclinazione della tangente in B è eguale a ΔRT/Δq = 5/1 = 5€, che definiamo
ricavo marginale. Analogamente, la fig.4 mostra il prezzo conveniente per Leandro come rapporto l'incasso totale AB e la quantità venduta OA: il suo 'profitto' è massimo vendendo la
quantità che eguaglia ricavo marginale a costo marginale (costante, perché qui si tratta di una
retta).
7. Possiamo allora fare un passo avanti, riportando in un grafico ad hoc (= appropriato alla situazione) i valori medi e marginali delle successive quantità vendibili.
Le due parti della fig.5 mostrano il passaggio dai ricavi totali a quelli medi, prendendo a riferimento tre punti. Nel punto A, alla vendita di 100 melograni corrisponde un ricavo totale di
1.000€ e, quindi, un ricavo unitario (=medio) di 10€: informazione trasferita nella figura in basso, riportando quel prezzo lungo l'asse verticale, in corrispondenza della stessa quantità OA'.
Ripetendo l'operazione per tutti gli altri punti (come B e D), otteniamo in basso i ricavi medi di
Leandro: notare come questi ricavi medi esprimano la domanda degli acquirenti, vale a dire le
informazioni riportate nelle prime due colonne della tabella di partenza!
L'area dei rettangoli d'ogni punto della domanda indica (come illustrato per il punto C), allora,
il ricavo totale corrispondente. Le aree come moltiplicazione, quindi: se moltiplichiamo O'D'
(=300) per il pvendita di 6 euro, otteniamo i 1.800 indicati da D'D in alto.
3
2009-10 Prof. G. Galeotti – Materiali
8. I grafici della fig. 6 mostrano il passaggio dai ricavi totali a quelli marginali, collegando di nuovo le quantità via via vendute ai ricavi marginali indicati dalle inclinazioni delle rette tangenti ai
RT. Il passaggio è illustrato per gli stessi 3 punti precedenti. Si noti come i ricavi marginali diRicavi
totali
DAI RICAVI TOTALI AI RICAVI
MEDI
1.800
B
1.600
Ricavi
totali
DAI RICAVI TOTALI
AI RICAVI MARGINALI
D
D
R
T
8
B
R
T
4
HD=800
10
1.000
A
A
8
6
O
A'=100
10
B'=200
q
D'=300
q
A'=100
Ricavi
marginali
Ricavi medi = RT/q = domanda dei consumatori
8
B'=200
D'=300
Ricavi marginali = ΔRT/Δq
8
6
L'area del triangolo
ombreggiato esprime
il ricavo totale HD
(in alto)
C
L'area del rettangolo
ombreggiato esprime
il ricavo totale D'D
Ricavi totali
O' A'
H
B'
(in alto)
4
0
A'
D'
Fig. 5
Ricavi totali
B'
D'
Fig. 6
Costi totali
minuiscano più rapidamente di quelli medi, annullandosi per q=OD'. Quando in alto la retta
tangente è parallela all'asse orizzontale, l'inclinazione è nulla e il ricavo marginale pari a zero.
In questo caso, i ricavi totali sono indicati dall'area sottesa ai riCOSTI TOTALI CRESCENTI A
cavi marginali per il tratto preso in considerazione, come somTASSO COSTANTE
ma (area del triangolo ombreggiato) di tutti gli incrementi di ricavi procurati dalla vendita di A'D' melograni venduti e, quindi,
eguali al ricavo totale HD della figura in alto.
B 5
Procedimenti analoghi valgono per passare dai costi totali a
quelli medi e marginali. La fig.7 presenta il caso che stiamo
A 5
considerando, quello più semplice di costi costanti (cosicchè
C
O
costi medi e marginali coincidono).
A'
B'
9. Tanti grafici per capirne bene uno! Per quanto complicati a
prima vista, questi passaggi permettono di sintetizzare tutte le
informazioni rilevanti nella figura 10 da cui siamo partiti, che
presenta i 2 vincoli fronteggiati da Leandro: la domanda HF dei
consumatori e i costi unitari costanti OC che deve affrontare.
Per massimizzare il guadagno giornaliero, l'unica variabile che
controlla è pvendita, individuato per la quantità che eguaglia i costi marginali (qui costanti) ai ricavi marginali HL, che diminuiscono più rapidamente dei ricavi medi1: un risultato raggiunto
senza alcun calcolo (i numeri servono solo a fissare le idee).
Costi
5
O'
D
Costi medi costanti
(=costi marginali): l'area del rettangolo ombreggiato esprime il
costo totale di Leandro
per acquistare A'B'
frutti
E
A'
B'
Fig.7
8
10. Sinora abbiamo supposto che Leandro sia l'unico venditore di melograni nel mercato rionale: il
suo equilibrio è quindi quello di monopolio, mercato caratterizzato, appunto, dalla presenza di
1
Quando i prezzi di domanda presentano un profilo rettilineo, l'inclinazione dei ricavi marginali è doppia.
4
2009-10 Prof. G. Galeotti – Materiali
unico venditore2. Quando altri banchi si accorgono di quel guadagno cercheranno di sottrargli
clienti, vendendo i melograni a prezzi più bassi. Leandro reagirà abbassando il prezzo e gli altri
abbassandolo ulteriormente: sino a quando? In assenza d'accordi collusivi, il prezzo scenderà
sino a coprire i costi di acquisto della materia prima e di gestione del banco, incluso un guadagno minimo che renda l'attività conveniente. Le figure seguenti confrontano i due diversi equilibri, evidenziando che la rendita dei consumatori è
minore in caso di monopolio (area del triangolo BHE);
maggiore in caso di concorrenza (area del triangolo CHF);
nel confronto, il monopolista guadagna di più ma provoca una perdita di benessere: il triangolo indicato con il punto interrogativo che non va a vantaggio di nessuno.
Ricavi /
Costi
(€)H
DI MONOPOLIO
Vantaggio
per i clienti
B
E
Rendita di
monopolio
C
O
Ricavi /
Costi
(€)H
EQUILIBRIO
EQUILIBRIO
CONCORRENZIALE
Vantaggio
per i clienti
?
F
A
Fig. 5 Fig. 5 Fig. 5
Fig. 8
F
C
D
O
q
Fig. 5 Fig. 5 Fig. 5
Fig. 9
L
q
11. Il termine "rendita" proviene
Fig.12. MERCATO CONCORFig. 11: MERCATO CONRENZIALE DEL BENE X
CORRENZIALE
pX
dall'economista David Ricardo p grano
(indicati
i profitti di 2
DEL GRANO
(1772-1823) che la rapportava
imprese
intramarginali)
domanda
ai fattori produttivi irriproducidomanda
bili, come la terra coltivabile.
offerta
(
COSTI
PRODUZIONE
)
Ricardo partiva dall'ipotesi che,
offerta
con l'aumento della domanda di
Rendita dei terregrano, venissero messi a cultura
ni a fertilità
decrescente
terreni meno fertili: richiedendo
costi produttivi maggiori ed esq grano
qX
sendo il prezzo del grano idenTerreni (fertilità decrescente)
tico, l'ultimo terreno coltivato
era quello che garantiva la mera copertura dei costi di produzione. In questo modo, i terreni più
fertili (terreni intra-marginali) godevano di una rendita (fondiaria) indicata dal tratteggio verticale della fig. 11. La fig. 12 replica l'informazione nel caso di un bene prodotto industrialmente
da più imprese in concorrenza3. Notare: nel caso di concorrenza si parla di 'profitto' delle imprese, mentre in caso di monopolio si parla di 'rendita di monopolio'.
12. Nei casi di beni 'unici' (es.: quadri o tappeti persiani, supposti fatti a mano!), il monopolista
può chiedere prezzi diversi per ogni bene (ad es., vendendoli all'asta): in questo modo può appropriarsi pressoché dell'intera rendita dei consumatori. In altri casi, può vendere a prezzi diversi, ma chi acquista la stessa quantità paga lo stesso prezzo (es.: tariffe elettriche). In un 3° caso
può approssimare lo stesso obiettivo, vendendo uno stesso bene (o servizio) per gruppi di consumatori, come nel caso dei servizi ferroviari (1a e 2a classe), riduzioni per età o vendite last
minute.
2
Si tratta di un monopolio (spaziale) basato sui costi fronteggiati dagli acquirenti per procurarsi i melograni in
mercati più distanti, o acquistando ai mercati generali negli orari previsti per i non commercianti.
3
Occorre avere un'idea dei costi medi e marginali di un'impresa (rappresentati per le 3 imprese della fig.12).
5