TEORIA SUI LIMITI
DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
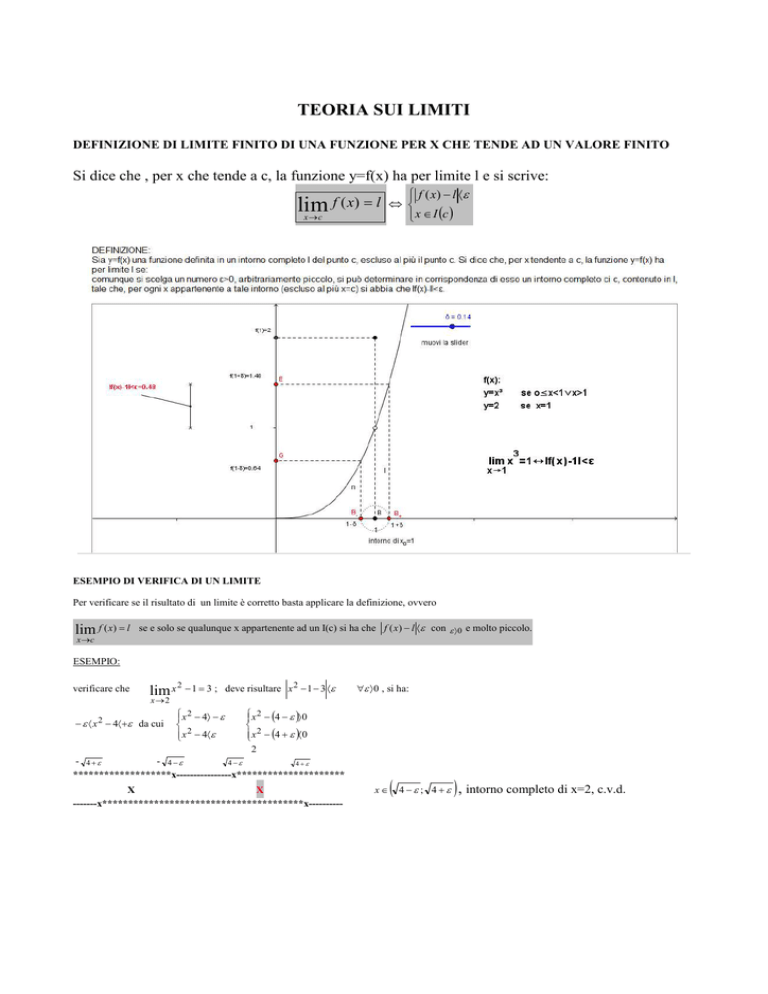
Si dice che , per x che tende a c, la funzione y=f(x) ha per limite l e si scrive:
lim f ( x) = l
x →c
f ( x) − l ⟨ε
⇔
x ∈ I (c )
ESEMPIO DI VERIFICA DI UN LIMITE
Per verificare se il risultato di un limite è corretto basta applicare la definizione, ovvero
lim f ( x) = l
x →c
se e solo se qualunque x appartenente ad un I(c) si ha che f ( x ) − l ⟨ε con ε ⟩ 0 e molto piccolo.
ESEMPIO:
verificare che
lim x
2
− 1 = 3 ; deve risultare x 2 − 1 − 3 ⟨ε
∀ε ⟩ 0 , si ha:
x→2
− ε ⟨ x 2 − 4⟨ +ε da cui
x 2 − 4⟩ − ε
2
x − 4⟨ε
x 2 − (4 − ε )⟩ 0
2
x − (4 + ε )⟨ 0
2
- 4+ε
- 4 −ε
4 −ε
4+ε
*******************x----------------x*********************
X
X
-------x***************************************x----------
x∈
( 4−ε ;
4+ε
) , intorno completo di x=2, c.v.d.
DEFINIZIONE DI LIMITE FINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE INFINITO
Si dice che , per x che tende a infinito, la funzione y=f(x) ha per limite l e si scrive:
lim f ( x) = l
x →∞
f ( x) − l ⟨ε
⇔
x ∈ I (∞ )
ESEMPIO DI VERIFICA DI UN LIMITE
Per verificare se il risultato di un limite è corretto basta applicare la definizione, ovvero
lim f ( x) = l
x →∞
se e solo se qualunque x appartenente ad un I( ∞ ) si ha che f ( x ) − l ⟨ε con ε ⟩ 0 e molto piccolo.
ESEMPIO:
verificare che
x −1− x
⟨ε ⇒
x
x −1
x −1
= 1 ; deve risultare
− 1 ⟨ε
x
x
x →∞
lim
−1
⟨ε ⇒
x
1
⟨ε
x
⇒ x >
1
ε
⇔ x<−
∀ε ⟩ 0 ⇒ un intorno di x=2; si ha
1
ε
∨x>+
1
ε
1 1
⇒ x ∈ − ∞;− ∪ + ;+∞ ⇒ x ∈ I (∞ ) ,
ε ε
c.v.d.
DEFINIZIONE DI LIMITE INFINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE FINITO
Si dice che , per x che tende ad un valore finito, la funzione y=f(x) ha per limite infinito e si scrive:
lim f ( x) = ∞
x →c
f ( x) > M
⇔
x ∈ I (c )
ESEMPIO DI VERIFICA DI UN LIMITE
Per verificare se il risultato di un limite è corretto basta applicare la definizione, ovvero
lim f ( x) = ∞
x →c
se e solo se qualunque x appartenente ad un I( c ) si ha che f ( x) > M con ∀ M ⟩ 0 e molto grande.
ESEMPIO:
verificare che
1
lim x = ∞ ;
x →0
1
>M ⇒
x
deve risultare
1
>M
x
1
1
1
1
>M ⇒ x <
⇒−
<x<
x
M
M
M
∀M ⟩ 0 ⇒ un intorno di infinito; si ha
1
1
⇒ x ∈ −
;+ ⇒ x ∈ I (0) ,
M M
c.v.d.
DEFINIZIONE DI LIMITE INFINITO DI UNA FUNZIONE PER X CHE TENDE AD UN VALORE INFINITO
Si dice che , per x che tende ad un valore finito, la funzione y=f(x) ha per limite infinito e si scrive:
lim f ( x) = ∞
x→∞
f ( x) > M
⇔
x ∈ I (∞ )
ESEMPIO DI VERIFICA DI UN LIMITE
Per verificare se il risultato di un limite è corretto basta applicare la definizione, ovvero
lim f ( x) = ∞
se e solo se qualunque x appartenente ad un I( ∞ ) si ha che f ( x) > M con M ⟩ 0 e molto grande.
x →∞
ESEMPIO:
verificare che
lim x
3
= ∞ ; deve risultare x 3 > M
∀M ⟩ 0 ⇒ un intorno di infinito; si ha
x →∞
x3 > M ⇒
x3 < − M ∨ x3 > + M ⇒
x<3 −M ∨ x>3 +M
(
) (
)
⇒ x ∈ − ∞; 3 − M ∪ 3 + M ;+∞ ⇒ x ∈ I (∞ ) ,
c.v.d.
TEOREMI SUI LIMITI
T: unicità del limite
Se per x che tende a c, finito o infinito,
lim
x→ ±c
f ( x ) = l , si ha che questo limite è unico.
T: della permanenza del segno
Se lim f ( x) = ±l ≠ 0 esiste un intorno di c per tutti i punti del quale, escluso al più c, l valori della
x → ±c
funzione hanno lo stesso segno del limite ovvero f(x)>0, se l>0 oppure f(x)<0 se l<0.
T1C: primo teorema del confronto
Se risulta f(x) ≤ g(x) ≤ h(x) e lim f ( x) = ±l e
x→±c
T2C: secondo teorema del confronto
Se risulta f ( x) ≤ g ( x) e lim g ( x) = 0
x →± c
lim h( x) = ±l
allora anche
x→±c
allora anche
lim
lim g ( x) = ±l
x→±c
f ( x) = 0
x → ±c
T3C: terzo teorema del confronto
Se risulta g ( x) ≥ f ( x) e lim f ( x) = ±∞ allora anche
x→±c
lim g ( x) = ±∞
x→±c
FUNZIONI CONTINUE
DEFINIZIONE: Una funzione di equazione y=f(x) si dice continua in un punto c quando esiste il
limite della funzione per x tendente a c e questo limite è uguale al valore della funzione in quel
punto, cioè quando si verificano le seguenti condizioni:
1) f(c)=l
2) lim f ( x) = l
x→c
3) lim f ( x) = f (c) = l
x →c
Sono continue le funzioni:
valori di continuità
o Costanti
f(x)=k
∀x ∈ ℜ
o Lineari
f(x)=x
∀x ∈ ℜ
o irrazionali con indice pari
f ( x) = 2 n x
x≥ 0
2
n
+
1
o irrazionali con indice dispari f ( x) =
x
∀x ∈ ℜ
x
o esponenziali
f ( x) = a
a>0
∀x ∈ ℜ
o logaritmiche
∀x ∈ ℜ
f ( x) = log a x a > 0, a ≠ 1
o goniometriche
f(x)=senx; f(x)=cosx
∀x ∈ ℜ
π
o goniometriche
f(x)=tanx
x ≠ + kπ
2
o goniometriche
f(x)=cotx
come si vede ogni funzione è continua nel proprio dominio.
x ≠ kπ
CALCOLO DEI LIMITI DI FUNZIONI CONTINUE
I limiti delle funzioni continue si possono calcolare sostituendo al posto della x il valore a cui
tendono.
Esempio:
lim 3
x
= f (3) = 3 2 = 9
x →2
TEOREMA: Limite della somma di due funzioni:
siano f(x) e g(x) due funzioni che ammettono, per x che tende a c (c finito o infinito), limiti finiti l1
ed l2, allora il limite della somma delle due funzioni esiste ed è la somma dei loro limiti:
lim(f(x)+g(x))=limf(x)+limg(x)= l1+l2
Si possono avere i seguenti casi:
a) lim (f(x)+k)= l1+k
b) l1=+ ∞ ed l2=+ ∞
lim( f+g)=+ ∞ + ∞ =+ ∞
c) l1=- ∞ ed l2=- ∞
lim (f+g)=- ∞ - ∞ =- ∞
d) l1=k ed l2=+ ∞
lim (f+g)=k+ ∞ =+ ∞
e) se dalla somma risulta [+ ∞ - ∞ ] si ha una FORMA INDETERMINATA.
SOMMA E DIFFERENZE DI FUNZIONI CONTINUE SONO FUNZIONI CONTINUE.
TEOREMA: Limite del prodotto di due funzioni:
siano f(x) e g(x) due funzioni che ammettono, per che tende a c (c finito o infinito), limiti finiti l1 ed
l2, allora il limite del prodotto di due funzioni esiste ed è il prodotto dei loro limiti:
lim(f(x)*g(x))=limf(x)*limg(x)= l1*l2
Si possono avere i seguenti casi:
f) lim (k f(x))= k l
g) l1=+ ∞ ed l2=+ ∞
lim( f+g)=+ ∞ *+ ∞ =+ ∞
h) l1=- ∞ ed l2=- ∞
lim (f+g)=- ∞ *(- ∞ )=+ ∞
i) lim (f(x))n=ln
j) se dal prodotto risulta [0 ⋅ ∞ ] si ha una FORMA INDETERMINATA.
IL PRODOTTO DI FUNZIONI CONTINUE IN UN INTERVALLO I E’ UNA FUNZIONE
CONTINUA NELLO STESSO INTERVALLO.
⇒ Le funzioni razionali intere ovvero i polinomi di grado n sono funzioni continue in R.
(
)
n
n
⇒ Limite di una potenza: lim f ( x ) = lim f ( x )
⇒ Limite del reciproco di una funzione:
lim
1
1
=
con l ≠ 0
f ( x) l
TEOREMA: Limite del quoziente di due funzioni:
siano f(x) e g(x) due funzioni che ammettono, per che tende a c (c finito o infinito), limiti finiti l1 ed
l2 ≠ 0, allora il limite del quoziente due funzioni esiste ed è il quoziente dei loro limiti:
lim(f(x)/g(x))=limf(x)/limg(x)= l1/l2
Si possono avere i seguenti casi:
k)
lim
k
k
=
con l ≠ 0
f ( x) l
l) Se l1=k ≠ 0 ed l2=0
m) Se l1= ∞ ed l2=l
⇒
n) Se l1=k ed l2= ∞
1
→0
o) ∞
;
⇒
lim
1
→∞
0
;
k
→∞
0
f ( x) k
= →∞
g ( x) 0
f ( x) ∞
= →∞
anche se l=0
g ( x) l
lim
⇒
k
→0
∞
lim
f ( x) k
= →0
g ( x) ∞
;
∞
→0
k
∞ 0
p) Se dal quoziente risulta e si hanno FORME INDETERMINATE.
∞ 0
IL QUOZIENTE DI FUNZIONI CONTINUE IN UN INTERVALLO I E’ UNA FUNZIONE
CONTINUA IN TUTTI I PUNTI DELLO STESSO INTERVALLO IN CUI RISULTA g(x) ≠ 0.
⇒ Le funzioni razionali fratte sono continue per tutti i valori di x che non annullano il
denominatore.
COME SI RISOLVONO ALCUNE FORME INDETERMINATE
Quando, nella risoluzione di un limite, si ottiene come risultato una forma indeterminata del tipo
∞ 0
∞−∞
0 ⋅ ∞ , si può calcolare il limite mettendo in pratica una “trasformazione” algebrica
∞ 0
della funzione o scomponendo e semplificando. Riassumiamo i casi più comuni:
CASO 1: limite per x che tende all’infinito di una funzione razionale di grado n
n
n −1
n−2
lim ax + bx + cx + .........
x → ±∞
Se si trova la forma indeterminata ∞ − ∞ si raccoglie la x di grado massimo e si ha che il limite da
calcolare è uguale al limite del termine di grado massimo ovvero
n
n −1
n−2
n
lim ax + bx + cx + ......... = lim ax
x → ±∞
x → ±∞
CASO 2: limite per x che tende ad un valore finito di una funzione fratta; se si trovano le forme
∞ 0
allora si devono scomporre numeratore e denominatore e semplificare la
indeterminate
o
∞ 0
frazione, prima di ricalcolare il limite.
CASO 3: limite per x che tende all’infinito di una funzione fratta; se si trovano le forme
∞ 0
allora si deve raccogliere la x di grado massimo sia al numeratore che al
indeterminate
o
∞ 0
denominatore e si ha che il limite sarà uguale al limite del rapporto dei termini di grado massimo.
RIEPILOGO ASINTOTI
L’asintoto è una retta a cui la curva che rappresenta la funzione nel piano cartesiano si avvicina
indefinitivamente senza toccarla mai (si dice che la curva è tangente all’asintoto all’infinito).
Possono esistere tre tipi di asintoti:
ASINTOTI VERTICALI
di equazione X= ± C
Esistono soprattutto per le funzioni fratte e si trovano per quei i valori che annullano il
denominatore; se esiste, l’asintoto verticale, si trova quando il limite per x che tende ad un valore
finito, tende all’infinito ovvero
lim f ( x) = ±∞
x→±c
ASINTOTI ORRIZZONTALI
di equazione Y= ± C
Se esiste, l’asintoto orizzontale, si trova quando il limite per x che tende all’infinito, tende ad un
valore finito ovvero
lim f ( x) = ±c
x → ±∞
ASINTOTI OBLIQUI
di equazione Y=mx+q
Se esiste, l’asintoto obliquo, si trova quando il limite per x che tende all’infinito, tende ad un valore
infinito ovvero
lim f ( x) = ±∞
x → ±∞
In tal caso se nel calcolo dei limiti si ottiene questo risultato, si deve procedere calcolando prima il
coefficiente angolare e poi l’ordinata all’origine q
f ( x)
m= lim
= ± c con c ≠ ∞ (il coefficiente angolare non può essere infinito)
x
x → ±∞
q= lim [ f ( x) − mx] = ±c
x → ±∞
(ovviamente se m=0 e se pure q=0 la retta non esiste).










