lezione urti

Urti
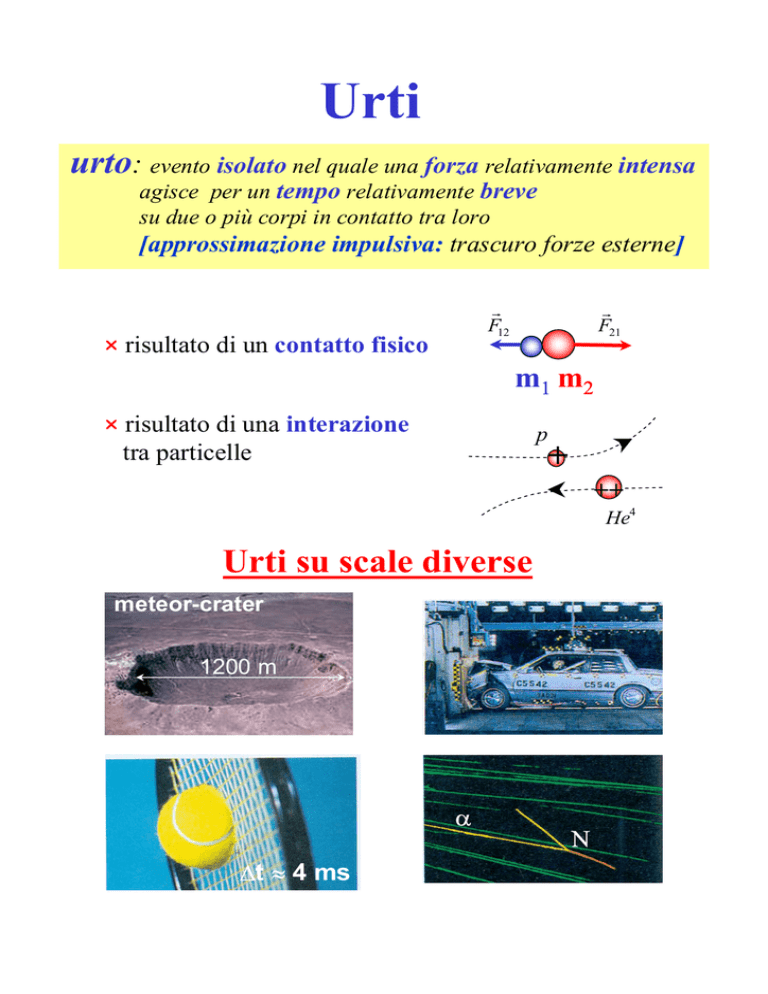
urto: evento isolato nel quale una forza relativamente intensa
agisce per un tempo relativamente breve
su due o più corpi in contatto tra loro
[approssimazione impulsiva: trascuro forze esterne]
r
r
F12
risultato di un contatto fisico
r
F21
m1 m2
r
risultato di una interazione
tra particelle
p
+
++
He4
Urti su scale diverse
meteor-crater
1200 m
α
∆t ≈ 4 ms
Ν
Quantità di Moto negli Urti
per ogni tipo di urto
la quantità di moto totale si conserva
L esercita su R forza F(t)
R esercita su L forza –F(t)
F(t) e –F(t) sono
coppia di forze azione e reazione:
intensità varia nel tempo
r intensità è uguale istante per istante
r
ti
∆pR = ∫ F (t ) dt
F
ti
F(t)
ti
∆pL = ∫ (− F (t )) dt
ti
∆pR = − ∆pL
t
- F(t)
∆pR + ∆pL = 0
r r
r
p = pR + pL = costante
le forze impulsive sono interne al sistema,
quindi NON influenzano la quantità di moto totale
Energia negli Urti
l’energia cinetica NON si conserva sempre negli urti
posso avere conversione in
energia termica
r energia acustica
r energia potenziale elastica (deformazione dei corpi)
r energia rotazionale
r
urto elastico:
energia cinetica totale
non cambia
( K tot ) i = ( K tot ) f
[es. urto fra bocce]
urto anelastico:
energia cinetica totale
non si conserva
( K tot ) i = ( K tot ) f + Eth + E pot + ...
[es. urto palla di gomma su pavimento]
urto perfettamente anelastico:
massima trasformazione
energia cinetica totale,
i due corpi rimangono uniti
[es. urto palla di plastilina su pavimento]
( K tot ) f ≠ ( K tot ) i
m f = mi ,1 + mi , 2
in tutti i casi la quantità di moto si conserva sempre
http://ww2.unime.it/weblab/ita/wf2/urti/urti_ita.htm
Urti in UNA dimensione
urto perfettamente anelastico
[conservo solo quantità di moto]
le particelle dopo l’urto
rimangono unite con velocità vf
prima
r
r
pi = p f
r
r
r
m1v1i + m2 v2i = (m1 + m2 )v f
r
r
r
m1v1i + m2 v2i
vf =
(m1 + m2 )
dopo
esempio: pendolo balistico
dispositivo per determinare
velocità dei proiettili
V =
m
v
(m + M )
conservazione
quantità di moto
1
( m + M )V 2 = ( m + M ) gh
2
v=
m+M
m
2 gh
conservazione
energia meccanica
v = 630 m / s
m = 9 .5 g M = 5 .4 kg
h = 6 .3 cm
trasformo alta velocità proiettile
in bassa velocità corpo pesante
[di facile misurazione]
urto elastico
[conservo quantità di moto ed energia cinetica]
r
r
pi = p f
r
r
r
r
m1v1i + m2 v2i = m1v1 f + m2 v2 f (1)
prima
( K tot ) i = ( K tot ) f
dopo
1
1
1
1
m1v12i + m2 v22i = m1v12f + m2 v22 f
2
2
2
2
bersaglio mobile v2i ≠ 0
r r
pi = p f
( K tot ) i = ( K tot ) f
⇒ m1 (v1i − v1 f ) = −m2 (v2i − v2 f )
⇒ m1 (v12i − v12f ) = − m2 (v22i − v22 f )
m1 (v1i + v1 f )(v1i − v1 f ) = − m2 (v2i + v2 f )(v2i − v1 f )
divido le due precedenti equazioni e sostituisco …
(v1i + v1 f ) = (v2i + v2 f )
(2) (v1i − v2i ) = −(v1 f − v2 f ) velocità relative uguali ed opposte
prima e dopo l’urto
N.B. note:
m1, m2
v1i, v2i
conservazione p (1)
+
velocità relative (2)
v1 f =
2m2
m1 − m2
v2 i
v1i +
m1 + m2
m1 + m2
v2 f =
2m1
m − m1
v2 i
v1i + 2
m1 + m2
m1 + m2
bersaglio fisso v2i = 0
r r
pi = p f
( K tot ) i = ( K tot ) f
⇒ m1 (v1i − v1 f ) = m2 v2 f
⇒ m1 (v1i + v1 f )(v1i − v1 f ) = m2 v22 f
divido le due precedenti equazioni e sostituisco …
v1 f =
m1 − m2
v1i
m1 + m2
v2 f =
2m1
v1i
m1 + m2
r masse
uguali [m1=m2]
v1 f = 0
scambio di velocità
v2 f = v1i
[es. urto fra bocce/palle da biliardo]
r bersaglio
massiccio [m2>>m1]
v1 f = −v1i
v2 f
 2m1 
v1i
= 
 m2 
r proiettile
v1 f = v1i
proiettile rimbalza indietro
[es. urto palla golf su palla cannone
palla da baseball su mazza]
massiccio [m1>>m2]
proiettile indisturbato, bersaglio scatta in avanti
v2 f = 2v1i [es. urto palla cannone su palla golf]
http://ww2.unime.it/weblab/ita/wf2/urti/urti_ita.htm
esempi: urto elastico
urto fra palle di biliardo uguali:
v1 f = 0
v2 f = v1i
pendolo multiplo: palline di uguale massa
rapida successione
di urti elastici:
ad ogni urto una palla si ferma e
palla successiva si muove
con stessa velocità
esercizi urti in una dimensione
Urti in DUE dimensioni
urto non frontale
(corpi non allineati
nella direzione del moto)
dopo urto i corpi
non si muovono
sullo stesso asse
⇒
prima
dopo
conservazione quantità di moto:
r
r
pi = p f
r
r
r
r
m1v1i + m2 v2i = m1v1 f + m2 v2 f
per componenti:
m1v1ix + m2 v2ix = m1v1 fx + m2 v2 fx
m1v1iy + m2 v2iy = m1v1 fy + m2 v2 fy
⇒
m1v1ix + 0 = m1v1 f cos θ + m2 v2 f cos φ
0 + 0 = m1v1 f sin θ − m2 v2 f sin φ
conservazione energia cinetica
[per urti elastici solamente!!!]
1
1
1
1
m1v12i + m2 v22i = m1v12f + m2 v22 f
2
2
2
2
esercizi urti in due dimensioni
Centro di Massa
palla lanciata in aria:
traiettoria parabolica
[tipo moto proiettile]
mazza da baseball lanciata in aria:
moto complicato e diverso per le varie parti
mazza = sistema di punti materiali
centro di massa: punto che si muove lungo
traiettoria parabolica
[tipo moto proiettile]
centro di massa di un corpo (o sistema di corpi):
punto che si muove come se
4 tutta la massa fosse lì concentrata
4 e le forze esterne agissero lì
permette di descrivere
moto complessivo del sistema meccanico
esempio: sistema di due particelle
collegate da sbarra rigida
[priva di massa]
M1 < M2
r
applico F vicino ad M1
sistema ruota in
senso orario
r
applico F vicino ad M2
sistema ruota in
senso anti-orario
r
applico F vicino al CM
sistema trasla
si muove come se tutta
la massa fosse concentrata
nel CdM
individuo centro di massa con questo esperimento !!
Posizione del centro di massa
posizione media della massa del sistema
xCM =
def
m1 x1 + m2 x2
m1 + m2
esempio:
x1=0, x2=d
se m1 = m2 ⇒ xCM= (x1+x2)/2
se m2 = 2m1 ⇒ xCM= 2/3 d
metà strada
vicino particella pesante
sistema n particelle in 3 dimensioni
xCM
yCM
m x + m2 x2 + m3 x3 + ... + mn xn
= 1 1
=
def
m1 + m2 + ... + mn
∑m x = ∑m x
M
∑m
m1 y1 + m2 y2 + m3 y3 + ... + mn yn
=
=
def
m1 + m2 + ... + mn
∑m y = ∑m y
M
∑m
m1 x1 + m2 z 2 + m3 x3 + ... + mn z n
=
m1 + m2 + ... + mn
∑m z = ∑m z
M
∑m
zCM =
def
i i
i i
i
i
i
i
i
i
i i
i
i i
nel linguaggio dei vettori:
P(xi,yi,zi)
z rr
i
vettore posizione:
r
r
r
r
ri = xi i + yi j + zi k
x
y
sistema di n particelle
r
r
r
r
rCM = xCM i + yCM j + zCM k =
r
1
rCM =
M
n
particella di coordinate (xi,yi,zi)
r
m
r
∑ ii
∑m x +∑m y +∑m z
i i
i
i
i
i
i i
i
M
vettore posizione CM
i =1
corpi rigidi [distribuzioni continue di materia]
r
1 r
rCM =
r dm
M∫
∑ ∆m x
1
x dm
∫
def
m
∆
→
0
i
M
M
∑ ∆mi yi → 1 y dm
yCM =
def
∆mi →0 M ∫
M
∆mi zi
1
∑
zCM =
→
z dm
def
∆mi →0 M ∫
M
xCM =
i i
→
N.B. se oggetto possiede simmetria
CM si trova su centro, asse o piano di simmetria
Moto di un Sistema di Particelle
Il CM è utile nella descrizione del moto del sistema
r
1
rCM =
M
n
r
m
r
∑ ii
i =1
r
r
r
r
MrCM = m1r1 + m2 r2 + ... + mn rn
r
r
r
r
MvCM = m1v1 + m2 v2 + ... + mn vn
r
r
r
r
MaCM = m1a1 + m2 a2 + ... + mn an
r
r dri
vi =
dt
r
r dvi
ai =
dt
r r
r
r le forze interne
r
MaCM = F1 + F2 + ... + Fn = ∑ Fest si elidono a due a due
[azione e reazione]
il CM si muove come particella di massa M
su cui agisce la risultante delle forze esterne
r
r
r
dptot
∑ Fest = MaCM = dt
N.B. sistema isolato:
r
r
r
dptot
∑ Fest =MaCM = dt = 0
⇒
r
r
ptot = MvCM = costante
esempi: moto centro di massa
fuoco artificiale
r
r
Fest = Fg
CM segue
traiettoria parabolica
[la stessa del razzo inesploso]
ballerina che fluttua in aria:
traiettoria testa-busto
orizzontale !!!
[non parabolica
come nel lancio di un corpo]
CM segue
traiettoria parabolica
esercizi centro di massa
Moto di un Sistema di Particelle
Il CdM è utile nella descrizione del moto del sistema
r
r
1
drCM
vCM =
=
dt
M
r
dri
∑ mi dt =
r
∑m v
i i
M
velocità CDM
⇓
r
r
r
r
MvCM = ∑ mi vi = ∑ pi = ptot
quantità di moto totale è pari alla
massa totale per la velocità del CdM
[moto particella massa M, velocità vCM]
r
r
1
dvCM
aCM =
=
dt
M
r
1
dvi
m
=
∑ i dt M
r
m
a
∑ ii
⇓
r somma forze esterne
r
r
MaCM = ∑ mi ai = ∑ Fi
(quelle interne si elidono a coppie)
r
r
r
dptot
=
=
F
M
a
∑ est CM dt
il CdM si muove come particella di massa M
su cui agisce la risultante delle forze esterne
sistema isolato:
r
∑ Fest =0
⇒
r
r
ptot = costante vCM = costante
conservazione quantità di moto
propulsione di un razzo
[sistema a massa variabile]
durante il moto si conserva la massa del sistema
[massa combustibile + massa navetta]
pi = p f
Mv = − dM U + ( M + dM )(v + dv) con dM < 0
u = (v + dv) − U
velocita` relativa prodotti di scarico
− dM u = M dv
−
dM
dv
u=M
dt
dt
Ru = Ma
dv = −u
dM
M
vf
Mf
vi
Mi
∫ dv = −u
∫
ove R=-dM/dt
spinta del razzo
(I0 equazione del razzo)
Mi
Mf
(II0 equazione del razzo)
v f − vi = u ln
dM
M
rapidita`
consumo conbustibile
devo diminuire la massa finale
per avere aumento di velocita`