Note sulla probabilità
Maurizio Loreti
Dipartimento di Fisica
Università degli Studi di Padova
Anno Accademico –
1
La distribuzione del χ2
0.6
N=1
N=2
N=3
N=5
N=10
0.5
0.4
0.3
0.2
0.1
0
0
5
10
15
20
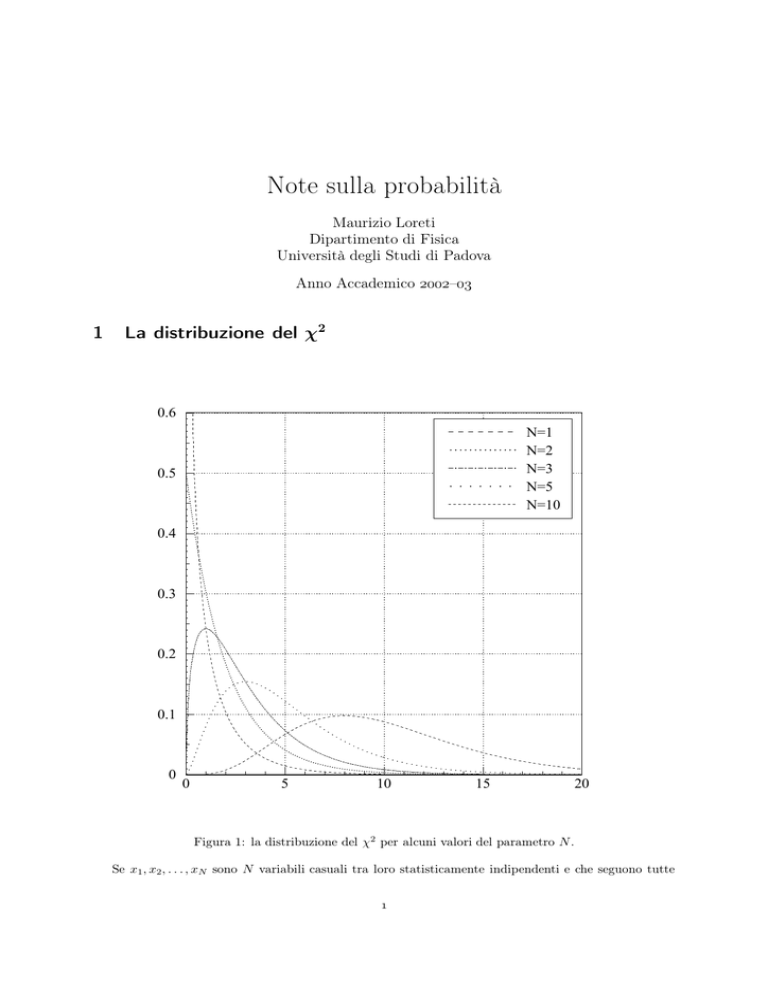
Figura 1: la distribuzione del χ2 per alcuni valori del parametro N .
Se x1 , x2 , . . . , xN sono N variabili casuali tra loro statisticamente indipendenti e che seguono tutte
1 - La distribuzione del χ2
la distribuzione normale standardizzata (ovvero la distribuzione di Gauss con media 0 e varianza 1), si
può dimostrare che la nuova variabile casuale
X=
N
X
xi 2
i=1
(ovviamente non negativa) è caratterizzata da una densità di probabilità ben determinata che si chiama distribuzione del chi quadro; il parametro N prende il nome di numero di gradi di libertà della
distribuzione.
Dalla definizione discende immediatamente la cosiddetta regola di somma del χ2 : ovvero, se X ed
Y sono due variabili casuali statisticamente indipendenti entrambe distribuite come il χ2 con N ed M
gradi di libertà rispettivamente, la loro somma Z = X + Y è una variabile casuale ancora distribuita
come il χ2 ; però con N + M gradi di libertà.
Speranza matematica e varianza di una variabile casuale X distribuita come il χ2 ad N gradi di
libertà valgono
(
E(X)
= N
Var(X)
=
2N
Inoltre, come si può supporre osservando la figura 1, anche la distribuzione del χ2 tende ad una distribuzione normale (avente la stessa media N e la stessa varianza 2N ) al crescere di N ; tale approssimazione
si può ritenere in pratica già buona quando N è superiore a 30.
1.1
Verifica delle ipotesi col metodo del χ2
La distribuzione del χ2 viene spesso usata per verificare la bontà dell’accordo tra una ipotesi teorica
e dei dati sperimentali. Come esempio, si pensi ad un campione di misure ripetute {x1 , x2, . . . , xN } che
si ritiene provengano da una distribuzione normale avente media ed errore quadratico medio noti a priori
x∗ e σ ∗ : ammessa per assurdo vera questa ipotesi, la variabile casuale
X=
2
N X
xi − x∗
i=1
σ∗
dovrebbe essere distribuita come il χ2 con N gradi di libertà.
L’ipotesi può essere rigettata se il valore calcolato di X è ritenuto troppo grande per poter essere
ottenuto sulla base della pura casualità: in pratica bisogna fissare arbitrariamente un valore della probabilità ε che segni il confine tra quelle fluttuazioni ritenute accettabili sulla base della pura casualità
e quelle cosí grandi da farci piuttosto ritenere che sia invece falsa l’ipotesi di partenza; normalmente si
sceglie ε = 99.7% oppure ε = 99%. Operata la scelta, si calcola con l’aiuto delle apposite tabelle quel
valore X0 che divide la curva del χ2 ad N gradi di libertà in due parti con area rispettivamente ε (a
sinistra di X0 ) e 1 − ε (a destra); se X > X0 l’ipotesi viene rigettata (ad un livello di confidenza ε), ed
accettata altrimenti.
Un metodo alternativo è quello di calcolare l’area ε sotto la curva del χ2 ad N gradi di libertà
nell’intervallo [X, +∞]: quanto maggiore è questo valore, tanto migliore è l’accordo con l’ipotesi.
Nel caso che media e varianza della distribuzione normale con cui si esegue il confronto non siano
note a priori ma vengano ricavate dal campione stesso attraverso le note formule
x̄ =
N
1 X
xi
N
N
σx 2 =
e
i=1
1 X
2
(xi − x̄)
N −1
i=1
si può dimostrare che la variabile
X=
N
2
X
(xi − x̄)
i=1
σx 2
1.2 - Dati in istogramma
è ancora distribuita come il χ2 : ma il numero di gradi di libertà è in questo caso N − 2. Questo è
conseguenza di una legge generale, secondo la quale:
Il numero di gradi di libertà da associare a variabili che seguono la distribuzione del χ2 è
dato dal numero di contributi indipendenti (ovvero dal numero di termini con distribuzione
normale standardizzata sommati in quadratura: qui N , uno per ogni determinazione xi )
diminuito del numero di parametri che compaiono nella formula e che sono stati ottenuti o
stimati dai dati stessi (qui due: la media della popolazione e la sua varianza).
1.1.1
Esercizi
Esercizio 1.1: si sono misurati gli angoli interni di 100 triangoli; i risultati sono riassunti nella tabella
seguente:
179.3
180.0
180.2
179.9
180.2
180.2
180.4
179.7
180.0
179.0
180.1
179.8
181.3
179.3
179.3
180.1
180.1
179.9
179.7
179.9
179.5
179.6
180.5
180.4
179.8
180.2
179.3
180.3
179.7
180.1
179.7
179.9
180.8
179.9
180.8
180.3
179.7
180.0
180.0
180.7
179.1
180.1
180.2
180.0
181.2
179.5
180.6
180.0
179.6
179.9
179.9
180.2
179.8
179.9
181.0
179.9
180.5
179.4
180.4
180.0
179.7
180.8
180.2
181.2
180.3
181.1
179.4
180.0
179.9
180.0
179.9
180.9
179.8
181.0
180.0
180.1
179.3
180.2
180.3
179.7
179.8
180.5
180.7
180.1
180.1
179.7
180.3
180.0
180.0
179.7
180.4
180.0
180.7
179.6
180.1
180.7
180.7
180.3
181.2
180.0
Si chiede di verificare l’ipotesi che i dati provengano da una popolazione normale.
1.2
Dati in istogramma
Se vogliamo verificare col metodo del χ2 l’ipotesi che dei dati già istogrammati (dopo aver diviso
in classi di frequenza i valori di una variabile casuale x) provengano da una densità di probabilità
corrispondente ad una funzione nota f(x), le cose sono piú complesse. Ammessa per assurdo vera
l’ipotesi:
1. La probabilità che una misura cada nella i-esima classe di frequenza, pi , è data dall’integrale di
f(x) sulla classe stessa.
2. I possibili valori del numero effettivo di misure che cadono in ogni classe si presenteranno secondo la
distribuzione binomiale; quindi il numero medio di eventi atteso nella generica classe vale Ai = N pi
e la sua varianza σi 2 = N pi (1 − pi ).
3. Se è lecito confondere in ogni classe la binomiale con una distribuzione normale, la variabile
X=
2
M X
Ai − Oi
i=1
σi
(1.1)
(M è il numero delle classi, ed Oi il numero di eventi effettivamente osservati in ognuna di esse)
segue la distribuzione del χ2 .
4. Se poi è anche lecito confondere in ogni classe la binomiale con una distribuzione di Poisson (quindi
se pi 1; che implica pi 2 pi e quindi σi 2 ≈ N pi = Ai ), la formula (1.1) diventa
X=
M
2
X
(Ai − Oi )
i=1
Ai
(1.2)
1 - La distribuzione del χ2
5. Il numero di gradi di libertà della distribuzione è M − 1: infatti M sono i contributi normali
indipendenti alla (1.1) e nei valori di tutte le Ai compare N che è ricavato dal campione; o, se
la f(x) dipendesse anche da R parametri ricavati dal campione, il numero di gradi di libertà
diventerebbe M − R − 1.
Il punto 3 è verificato se in ognuna delle classi Ai & 5; se cosí non fosse (e se la definizione delle
classi è lasciata allo sperimentatore) si possono eventualmente accorpare piú classi. Il punto 4 si può
considerare soddisfatto se in ogni classe pi non supera il 10 ÷ 15 per cento.
1.2.1
Esercizi
Esercizio 1.2: nell’esperienza dei pendoli, le 100 misure dirette del periodo sono riassunte (già divise
in classi di frequenza) nella tabella seguente:
t (s)
ni
t (s)
ni
1.750 − 1.775
1.775 − 1.800
1.800 − 1.825
1.825 − 1.850
1.850 − 1.875
1.875 − 1.900
1.900 − 1.925
1.925 − 1.950
1.950 − 1.975
1.975 − 2.000
0
0
2
3
3
5
7
5
6
13
2.000 − 2.025
2.025 − 2.050
2.050 − 2.075
2.075 − 2.100
2.100 − 2.125
2.125 − 2.150
2.150 − 2.175
2.175 − 2.200
2.200 − 2.225
2.225 − 2.250
18
17
11
6
3
1
0
0
0
0
Si chiede di verificare se i dati sono in accordo con l’ipotesi di una distribuzione normale.
Esercizio 1.3: in uno dei suoi esperimenti, l’abate Mendel osservò forma e colore dei frutti di molte
piante di piselli, classificandole in quattro categorie come segue (Oi è qui il numero di piante osservate
in ogni categoria):
i
Tipo
Oi
1
2
3
4
Rotondi e gialli
Rotondi e verdi
Oblunghi e gialli
Oblunghi e verdi
315
108
101
32
Totale
556
Sulla base delle sue teorie Mendel si aspettava un rapporto tra le popolazioni delle quattro categorie
di 9 : 3 : 3 : 1; i risultati sono in accordo con queste previsioni?
Esercizio 1.4: il Bortkewitch studiò il numero di morti per calci di cavallo nell’esercito prussiano,
registrando i decessi verificatisi in 10 corpi d’armata nel corso di 20 anni (per un totale quindi di N = 200
casi). Le frequenze assolute ni del numero di morti per corpo d’armata e per anno i sono riassunte nella
tabella seguente; si chiede di verificare se i dati sono in accordo con la distribuzione di Poisson.
i
ni
0
1
2
3
4
109
65
22
3
1
Totale
200
2
Soluzione degli esercizi
Esercizio 1.1:
media ed errore quadratico medio del campione valgono x̄ = 180.092 e σx = 0.48; inoltre
X=
2
100 X
xi − x̄
i=1
σx
≈ 99
Un valore almeno pari ad X viene ottenuto da una distribuzione del χ2 a 98 gradi di libertà nel 45.3%
dei casi; quindi l’accordo è buono.
Esercizio 1.2:
20
15
10
5
0
1.8
1.9
2
2.1
2.2
Figura 2: misure dirette del periodo con il pendolo.
media ed errore quadratico medio del campione valgono x̄ = 1.9958 e σ = 0.072518; nella figura 2 è disegnato l’istogramma dei dati assieme alla funzione di Gauss “di riferimento” (normalizzata all’istogramma).
Nella tabella seguente vi sono i dati necessari al calcolo del χ2 :
2 - Soluzione degli esercizi
t (s)
pi
Ai
Oi
< 1.900
1.900 − 1.925
1.925 − 1.950
1.950 − 1.975
1.975 − 2.000
2.000 − 2.025
2.025 − 2.050
2.050 − 2.075
2.075 − 2.100
> 2.100
0.093242
0.071213
0.099379
0.12329
0.13597
0.13331
0.11619
0.09003
0.06201
0.075375
9.3242
7.1213
9.9379
12.329
13.597
13.331
11.619
9.003
6.201
7.5375
13
7
5
6
13
18
17
11
6
4
(si sono unite alcune classi in modo da avere Ai & 5 in ogni intervallo). La formula (1.2) ci permette di
calcolare X ≈ 13.42, che va confrontato con la distribuzione del χ2 a 7 gradi di libertà; la probabilità che
per motivi casuali si presenti un valore non inferiore a quello trovato è solo del 6.26%: quindi l’accordo
è assai cattivo.
Esercizio 1.3:
il numero totale di osservazioni è N = 556; secondo la teoria quindi il numero di eventi Ai attesi nelle
varie categorie sarebbe:
i
1
2
3
4
pi
9
16
3
16
3
16
1
16
9
N
16
3
N
16
3
16 N
1
16 N
= 0.5625
= 0.1875
= 0.1875
= 0.0625
Ai
Oi
N pi q i
= 312.75
315
136.83
= 104.25
108
84.70
= 104.25
101
84.70
= 34.75
32
32.58
La variabile casuale
X=
4
2
X
(Ai − Oi )
i=1
Ai
≈ 0.47
dovrebbe essere distribuita come il χ2 a 3 gradi di libertà; in realtà la prima classe contiene il 56.25%
degli eventi attesi, per cui è meglio usare la (1.1) invece della (1.2). Quindi
X=
4
2
X
(Ai − Oi )
i=1
N pi q i
≈ 0.56
Secondo le tabelle, un valore inferiore a quello osservato si presenta casualmente nel 3.26% dei casi (e
quindi nel 96.74% dei casi il valore è almeno pari a quello osservato); quindi i risultati sono in accordo
piú che ottimo con la teoria.
Esercizio 1.4:
il numero medio di morti per corpo d’armata e per anno è
α =
4
1 X
i · ni ≈ 0.61
N i=0
Nella seguente tabella sono riportate le probabilità pi (calcolate dalla distribuzione di Poisson), il numero
atteso Ai = N pi di decessi ed il numero osservato ni ; i dati per i > 1 sono stati poi raggruppati in un’unica
classe:
i
pi
Ai
ni
N pi q i
0
1
0.5434
0.3314
108.67
66.29
109
65
49.62
44.32
2
3
4
0.1011
0.0206
0.0031
20.22
4.11
0.63
22
3
1
18.17
4.03
0.62
>1
0.1252
25.04
26
21.91
100
50
0
-1
0
1
2
3
4
5
Figura 3: i dati sperimentali (istogramma) confrontati con le previsioni della teoria (cerchi), per l’esercizio
1.4; in linea tratteggiata e con un quadrato sono rappresentati, rispettivamente, i dati e le previsioni per
i > 1.
La variabile casuale
X=
(109 − 108.67)2 (65 − 66.29)2 (26 − 25.04)2
+
+
≈ 0.06278
108.67
66.29
25.04
è distribuita come il χ2 a 1 grado di libertà; come nell’esercizio 1.3 le prime due classi corrispondono a
2 - Soluzione degli esercizi
pi elevati, per cui è meglio usare la (1.1) invece della (1.2):
X=
(109 − 108.67)2 (65 − 66.29)2 (26 − 25.04)2
+
+
≈ 0.08165
49.62
44.32
21.91
Quindi la probabilità di ottenere per motivi puramente casuali un valore almeno pari a quello osservato
è del 77.51%, e quindi i dati sono in ottimo accordo con l’ipotesi di una distribuzione di Poisson; nella
figura 3 la distribuzione teorica è confrontata poi coi dati sperimentali.