Triangoli Rettangoli

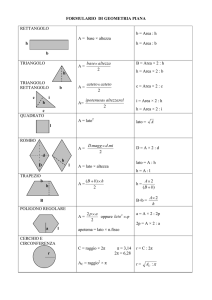
I TRIANGOLI
CLASSIFICAZIONE - RIPASSO
 Scaleno: angoli e lati diversi
 Isoscele: due lati e due angoli uguali
 Rettangolo: un angolo retto (2 cateti e l’ipotenusa)
 Equilatero: tre lati e tre angoli uguali (angoli di 60°)
AREA DI UN TRIANGOLO RETTANGOLO
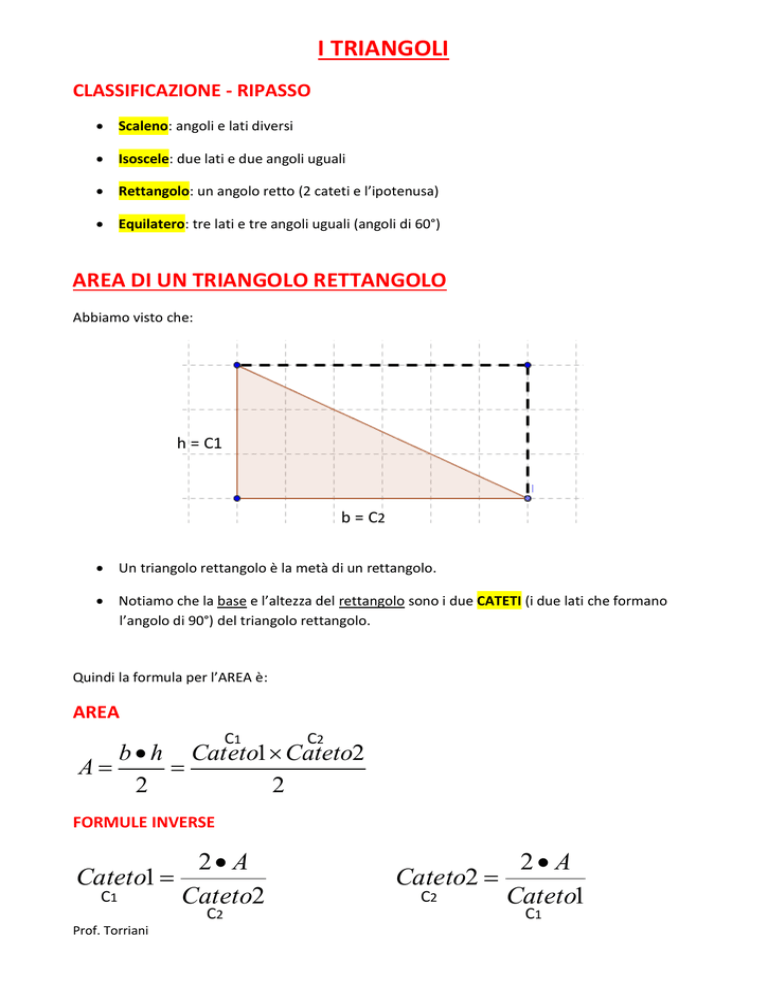
Abbiamo visto che:
h = C1
b = C2
 Un triangolo rettangolo è la metà di un rettangolo.
 Notiamo che la base e l’altezza del rettangolo sono i due CATETI (i due lati che formano
l’angolo di 90°) del triangolo rettangolo.
Quindi la formula per l’AREA è:
AREA
C1
C2
b  h Cateto1 Cateto2
A

2
2
FORMULE INVERSE
Cateto1 
C1
2 A
Cateto2
C2
Prof. Torriani
Cateto2 
C2
2 A
Cateto1
C1
 Esiste un altro modo per calcolare l’AREA:
Altezza relativa all’ipotenusa
Guarda la figura:
i
h = C1
b = C2
CH è l’altezza relativa all’ipotenusa e quindi:
h
i
C H  A B Altezza  Ipotenusa
A

2
2
FORMULE INVERSE
i
Ipotenusa 
2 A
Altezza
h
Prof. Torriani
h
Altezza 
2 A
Ipotenusa
i
PERIMETRO DI UN TRIANGOLO RETTANGOLO: caso particolare
ESERCIZIO
In un triangolo rettangolo un cateto vale 12 cm e l’altro vale 16 cm; se l’altezza relativa all’ipotenusa vale
9,6 cm, calcola il perimetro del triangolo.
IDEA
i
Confronto le due formule per l’area:
h
C1
C2
Altezza  Ipotenusa Cateto1 Cateto2
A

2
2
C
C
i
h
Altezza  Ipotenusa  Cateto1  Cateto2
Deve valere che:
1
2
Da questa ricavo che:
i
Ipotenusa 
C2
C1
Cateto1 Cateto2
Altezza
h
FORMULE INVERSE
C1 
h
ih
C2
C1 C 2
i
Prof. Torriani
C1
Cateto1 
h
i
Ipotenusa Altezza
Cateto2
C2
h
Altezza 
C2
C1
Cateto1 Cateto2
ipotenusa
i