Trasformatore
Parte 1
Trasformatore monofase
www.die.ing.unibo.it/pers/mastri/didattica.htm
(versione del 30-11-2010)
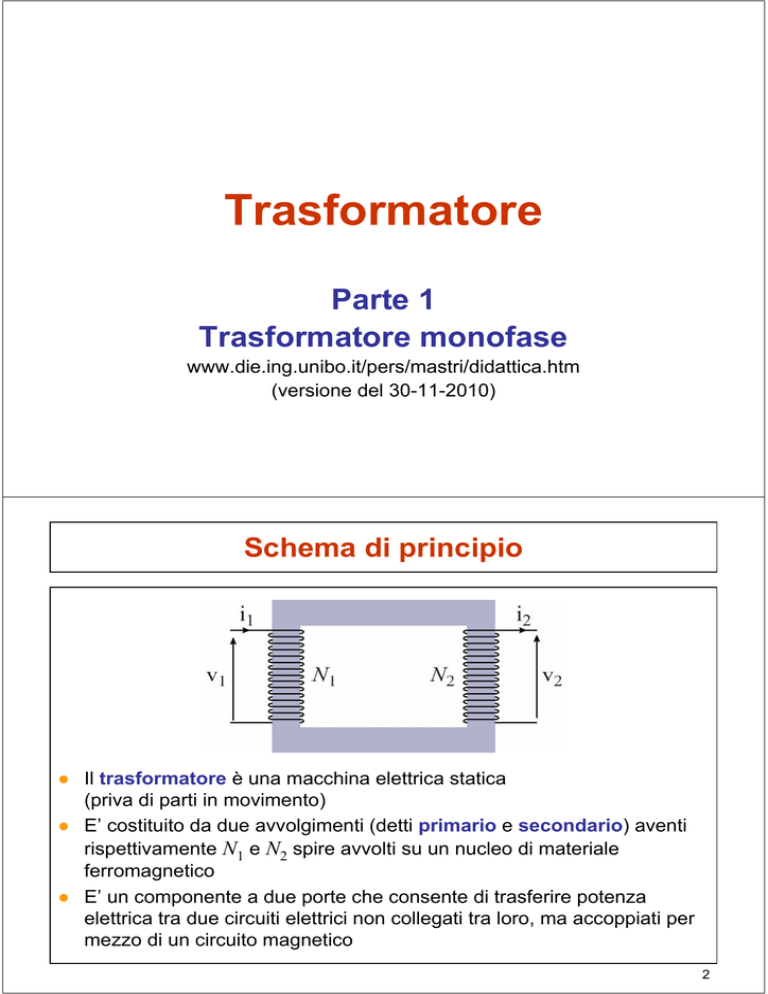
Schema di principio
● Il trasformatore è una macchina elettrica statica
(priva di parti in movimento)
● E’ costituito da due avvolgimenti (detti primario e secondario) aventi
rispettivamente N1 e N2 spire avvolti su un nucleo di materiale
ferromagnetico
● E’ un componente a due porte che consente di trasferire potenza
elettrica tra due circuiti elettrici non collegati tra loro, ma accoppiati per
mezzo di un circuito magnetico
2
Ipotesi sul campo magnetico
● Se gli avvolgimenti sono percorsi da corrente viene generato un campo
magnetico
● Si assume che le linee di flusso abbiano andamenti qualitativi
corrispondenti ai tre tipi indicati in figura
linee che si sviluppano interamente nel nucleo e si concatenano con
entrambi gli avvolgimenti
linee che si sviluppano in parte in aria e si concatenano con un solo
avvolgimento
3
Flussi di induzione magnetica (1)
● Il flusso di induzione magnetica dovuto a linee di campo che si
concatenano con entrambi gli avvolgimenti è detto flusso principale
● I flussi concatenati con il solo avvolgimento primario o il solo
avvolgimento secondario sono detti flussi di dispersione
La riluttanza dei tubi di flusso di dispersione è determinata
prevalentemente dai tratti in aria
è sempre lecito trascurare gli effetti di non linearità del nucleo e
assumere che i flussi di dispersione siano proporzionali alle correnti
d 1 Ld 1i1
d 2 Ld 2i2
Ld1, Ld2 induttanze di dispersione
Ld1 e Ld2 sono correlate ai soli flussi dispersi, quindi non
rappresentano le induttanze dei due avvolgimenti
4
Flussi di induzione magnetica (2)
● Flussi totali concatenati con gli avvolgimenti
c1 N1 d 1 N1 Ld 1i1
c 2 N 2 d 2 N 2 Ld 2i2
5
Equazioni interne
● Circuito primario
v1 (t ) R1 i1 (t )
d c1
di
d
R1 i1 (t ) Ld 1 1 N1
dt
dt
dt
R1 resistenza dell’avvolgimento primario
● Circuito secondario
v 2 (t ) R2 i 2 (t )
d c 2
di
d
R2 i 2 (t ) Ld 2 2 N 2
dt
dt
dt
R2 resistenza dell’avvolgimento secondario
● Circuito magnetico
N1 i1 N 2 i 2 R
R riluttanza del nucleo
6
Equazioni in condizioni di regime sinusoidale
● Ipotesi
Il primario è alimentato da una tensione v1(t) sinusoidale
Il secondario è collegato a un carico lineare
E’ possibile trascurare gli effetti non lineari nel nucleo
In condizioni di regime tutte le grandezze dipendenti dal tempo
variano con legge sinusoidale
E’ possibile applicare la trasformata di Steinmetz alle equazioni
interne
V1 ( R1 jLd 1 )I1 jN1Φ
V2 ( R2 jLd 2 )I 2 jN 2Φ
N 1 I 1 N 2 I 2 RΦ
7
Effetti dissipativi in un trasformatore
● Nel modello sviluppato fino a a questo punto si è tenuto conto solo degli
effetti dissipativi dovuti alle resistenze degli avvolgimenti
“perdite nel rame”
● Altri fenomeni dissipativi avvengono all’interno del nucleo magnetico
“perdite nel ferro”
Perdite per correnti parassite (correnti di Foucault)
Se il flusso di induzione magnetica nel nucleo varia nel tempo
all’interno del nucleo si hanno delle forze elettromotrici indotte
A causa della conducibilità del materiale ferromagnetico
all’interno del nucleo si hanno delle correnti
Dissipazione di energia per effetto Joule
Perdite per isteresi
8
Correnti parassite (1)
● Induzione magnetica B uniforme, ortogonale alle sezioni trasversali e
variabile con legge sinusoidale
B(t ) BM cos t
● Si può pensare che in ogni sezione trasversale del nucleo esistano dei
circuiti elettrici elementari
● Se S indica l’area della sezione racchiusa da un circuito elementare, il
flusso concatenato è
SBM cos t
Forza elettromotrice indotta
e
d
SBM sen t EM sen t
dt
Se R è la resistenza di un circuito elementare,
la potenza media dissipata in un periodo è
1 EM2 2 S 2 BM2
Pd
2 R
2R
9
Correnti parassite (2)
● La trattazione precedente giustifica intuitivamente la formula
semiempirica
pCP K CP f 2 BM2
pCP
f
BM
KCP
potenza dissipata per unità di peso del materiale
frequenza
induzione massima
costante dipendente dalla forma della sezione e dal
materiale (inversamente proporzionale alla resistività)
● Per ridurre le perdite dovute alle correnti parassite
si utilizzano leghe ad elevata resistività (ferro-silicio)
si ricorre alla laminazione del nucleo
10
Laminazione del nucleo (1)
● Il nucleo è formato da sottili lamierini sovrapposti e isolati tra loro
● Le correnti parassite si possono richiudere solo all’interno dei lamierini
i percorsi interessati dalle correnti parassite hanno sezione minore
resistenza più elevata
a parità di f.e.m. indotta si hanno correnti minori
l’area delimitata dalle linee di corrente è minore
riduzione del flusso concatenato e quindi della f.e.m. indotta
11
Laminazione del nucleo (2)
● Nel caso di un nucleo laminato, la potenza dissipata per unità di
peso può essere espressa mediante la relazione
pCP kCP 2 f 2 BM2
pCP
f
BM
kCP
potenza dissipata per unità di peso del materiale
frequenza
induzione massima
spessore di un lamierino
costante dipendente dal materiale
12
Perdite per isteresi
● Ad ogni ciclo di isteresi corrisponde un’energia dissipata per unità di
volume pari all’area racchiusa dal ciclo stesso
Le perdite per isteresi nel nucleo di un trasformatore dipendono
dal numero di cicli di isteresi nell’unita di tempo, determinato dalla
frequenza f
dall’area del ciclo di isteresi, determinata dal valore massimo
dell’induzione magnetica BM
La potenza dissipata può essere espressa mediante la formula
semiempirica
pI k I f BM1.6
pI
f
BM
kI
potenza dissipata per unità di peso
frequenza
induzione massima
costante dipendente dal materiale
13
Dipendenza dalle tensioni e dalla frequenza
2 2 2
● Perdite per correnti parassite: pCP kCP f BM
1.6
● Perdite per isteresi: p I k I f BM
● Se si trascura la caduta di tensione su R1 e Ld1 si ha
V1 jN1Φ j 2f N1SB
Se V1 è fissata, il valore massimo dell’induzione magnetica BM è
circa inversamente proporzionale alla frequenza
le perdite per correnti parassite sono praticamente costanti al
variare di f
le perdite per isteresi diminuiscono al crescere di f
Se f è fissata, BM è direttamente proporzionale all’ampiezza di v1(t)
le perdite aumentano all’aumentare dell’ampiezza di v1(t)
14
Rappresentazione delle perdite nel ferro
● Per tenere conto delle perdite nel ferro si può modificare il modello
introducendo un terzo avvolgimento fittizio caricato da una resistenza Rf
● Il valore della resistenza e il numero di spire dell’avvolgimento vanno
scelti in modo che la potenza dissipata su Rf coincida con la potenza
dissipata a causa delle perdite nel ferro
15
Rappresentazione delle perdite nel ferro
● Per l’avvolgimento fittizio vale la relazione
R f I f jN f Φ 0
I f j
Nf
Rf
Φ
● Con il terzo avvolgimento l’equazione del circuito magnetico diviene
N1 I 1 N 2 I 2 N f I f R Φ
cioè
N1I1 N 2 I 2 R jK f Φ
Kf
N 2f
Rf
Le equazioni interne diventano
V1 ( R1 jLd 1 )I1 jN1Φ
V2 ( R2 jLd 2 )I 2 jN 2Φ
N1I1 N 2 I 2 R jK f Φ
16
Trasformatore ideale (1)
● Il trasformatore ideale è caratterizzato dalle seguenti proprietà:
avvolgimenti con resistenza nulla R1 R2 0
assenza di flussi dispersi Ld1 = Ld2 0
nucleo con permeabilità infinita R 0
assenza di effetti dissipativi nel nucleo Kf 0
● In queste condizioni le equazioni interne divengono
V1 jN1Φ
V1
N1
V2
N2
I1
N2
I2
N1
V2 jN 2Φ
N1I1 N 2 I 2 0
17
Trasformatore ideale (2)
Equazioni caratteristiche
Simbolo
v1 (t ) K v 2 (t )
i1 (t )
K
1
i 2 (t )
K
N1
N2
rapporto di trasformazione (rapporto spire)
Potenza assorbita
1
p(t ) v1 (t ) i1 (t ) v 2 (t ) i 2 (t ) K v 2 (t ) i 2 (t ) v 2 (t ) i 2 (t ) 0
K
La potenza assorbita a primario viene trasferita integralmente in
uscita al secondario
18
Trasformazione dell’impedenza di carico
N
V1 1 V2
N2
I1
N2
I2
N1
V2 Z C I 2
2
N
N
V1 1 Z C I 2 1 Z C I1
N2
N2
2
V N
Z eq 1 1 Z C
I1 N 2
L’impedenza equivalente ai terminali del primario di un trasformatore
ideale con il secondario caricato da un impedenza ZC è pari all’impedenza di carico moltiplicata per il quadrato del rapporto spire
19
Trasferimento di impedenza (1)
N1
N
V2 1 V2 ZI 2
N2
N2
N
I 2 1 I1
N2
V1
2
N
N
V1 1 V2 1 ZI1
N2
N
2
V
1
Un impedenza in serie al secondario può essere portata in serie
al primario moltiplicata per il quadrato del rapporto spire
20
Trasferimento di impedenza (2)
N2
N
V
I2 2 I 2 2
N1
N1
Z
N
V2 2 V1
N1
I1
I1
N2
V1
I2
2
N1
N1 Z
N
I
1 2
Un impedenza in parallelo al secondario può essere portata in
parallelo al primario moltiplicata per il quadrato del rapporto spire
21
Corrente magnetizzante e corrente attiva (1)
● L’equazione del circuito magnetico può essere posta nella forma
N1I1 N 2 I 2 R jK f Φ
I1
N2
I 2 I I a
N1
Corrente magnetizzante
I
RΦ
N1
La corrente magnetizzante coincide con la corrente che circolando nell’avvolgimento primario con I2 0 produrrebbe il flusso
N1I RΦ
Corrente attiva
I a j
Kf
N1
Φ
La corrente attiva determina le perdite nel nucleo
22
Corrente magnetizzante e corrente attiva (2)
● Si indicano con E1 e E2 le f.e.m. dovute al flusso principale
E1 jN1Φ
E 2 jN 2 Φ
● La corrente attiva Ia è in quadratura con è in fase con E1
Si può porre
E1
jN1Φ
N12
R0
Kf
Ia
Kf
Φ
j
N1
R0 = resistenza di perdita del nucleo
● La corrente magnetizzante I è in fase con è in quadratura con E1
Si può porre
E1 jN1Φ
N12
jX 0
j
R
Φ
R
I
N1
X0 = reattanza magnetizzante
23
Circuito equivalente (1)
● Si riscrivono le equazioni interne facendo uso delle definizioni
precedenti
V1 ( R1 jLd 1 )I1 jN1Φ
V2 ( R2 jLd 2 )I 2 jN 2Φ
N1I1 N 2 I 2 R jK f Φ
E1 jN1Φ
I
RΦ
N1
I a j
j
Kf
N1
E1
X0
Φ
E1
R0
V1 ( R1 jLd 1 )I1 E1
V2 ( R2 jLd 2 )I 2
I1
N2
E1
N1
1
1
N2
E1
I 2 I I a j
N1
X0
R0
E’ possibile rappresentare
queste equazioni mediante
un circuito equivalente
24
Circuito equivalente (2)
V1 ( R1 jLd 1 )I1 E1
V2 ( R2 jLd 2 )I 2
I1
N2
E1
N1
1
N2
1
E1
I 2 I I a j
N1
R
X
0
0
25
Circuito equivalente riferito a primario
Si utilizza la proprietà di
trasferimento dell’impedenza
N12
R12 R2 2
N2
Ld 12
N12
Ld 2 2
N2
V12 V2
I12 I 2
N1
N2
N2
N1
26
Diagramma fasoriale (1)
● Si assume che il primario del trasformatore sia alimentato con una
tensione V1 e il secondario caricato da un’impedenza
ZC RC + jXC
● E’ possibile rappresentare il funzionamento del trasformatore mediante
un diagramma nel piano complesso costruito nel modo seguente:
Si assume (per comodità) uguale a zero la fase di
Si tracciano i vettori rappresentativi delle delle grandezze
direttamente legate a : I, Ia, I0, E1, E2
Nota ZC , da E2 si ricava I2
Si costruiscono i vettori rappresentativi di I12 e di I1
A partire da I1 e I2 si costruiscono i vettori rappresentativi delle
cadute di tensione dovute a R1, R2, Xd1, Xd2 e quindi si ottengono
V1 e V2
27
Diagramma fasoriale (2)
I
RΦ
N1
E1 jN1Φ
I a j
Kf
N1
Φ
I0 I a I
E 2 j N 2 Φ
I2
X X
E2
2 arctg d 2 C
R2 RC j ( X d 2 X C )
R2 RC
I12
N2
I2
N1
I1 I12 I 0
V1 E1 ( R1 jX d 1 )I1
V2 E 2 ( R2 jX d 2 )I 2
28
Diagramma fasoriale (3)
Note
● Il diagramma precedente si riferisce al caso di un’impedenza di
carico ohmico-induttiva (I2 in ritardo rispetto a V2)
● Per rendere più leggibile il diagramma I0 e le cadute di tensione
su R1, R2, Xd1, Xd2 sono state rappresentate fuori scala
(normalmente le loro ampiezze sono molto più piccole)
● A causa degli effetti reattivi nel trasformatore, in genere gli angoli
di sfasamento tra V1 e I1 e tra V2 e I2 risultano diversi
29
Circuiti equivalenti semplificati (1)
● Di solito la caduta di tensione su R1 e Ld1 è molto piccola
● In queste condizioni si ha E1 V1
Si può semplificare il circuito equivalente, spostando il ramo R0 - X0
In questo modo R1 e Ld1 risultano in serie con R12 e L12
R1cc
N12
R1 R12 R1 R2 2
N2
L1cc
N12
Ld 1 L12 Ld 1 Ld 2 2
N2
30
Circuiti equivalenti semplificati (2)
● Facendo uso della proprietà di trasferimento dell’impedenza, il ramo
R1cc L1cc può essere sostituito con un ramo posto in serie al secondario
R2 cc R1cc
N 22
N 22
R1 2 R2
N1
N12
L2 cc L1cc
N 22
N 22
Ld 1 2 Ld 2
N12
N1
31
Circuiti equivalenti semplificati (3)
● Se I0 è trascurabile rispetto a
I1 (come avviene in generale
per un trasformatore in condizioni nominali) è possibile semplificare ulteriormente i circuiti
equivalenti eliminando il ramo
formato da R0 e X0
reti equivalenti di Kapp
32
Indipendenza del flusso dalle condizioni di carico
● Se la caduta di tensione su R1 e Ld1 è trascurabile si ha
E1 jN1Φ V1
● Se V1 è fissato (come avviene normalmente) è fissato anche il valore
del flusso , che quindi risulta praticamente indipendente dalle condizioni di carico del trasformatore
Φ
V1
jN1
● Dall’equazione del circuito magnetico si ricava che deve essere
costante anche la quantità
N1I1 N 2 I 2 R jK f Φ
Se una variazione del carico produce una variazione della corrente del
secondario, il trasformatore reagisce con una variazione della corrente
del primario tale da mantenere costante la differenza tra i prodotti NI
(amperspire) a primario e secondario
33
Distorsione della corrente magnetizzante (1)
● Se il trasformatore è alimentato con una tensione v1(t) sinusoidale,
anche e1(t) e quindi (t) sono sinusoidali
● Se il nucleo non è lineare la corrente magnetizzante i(t) non può
essere sinusoidale, ma risulta distorta
● In particolare si può dimostrare che, in assenza di isteresi,
i(t) contiene armoniche dispari (pulsazione 3, 5 ecc.)
il contributo principale è costituito dalla terza armonica
(che risulta in opposizione con la fondamentale)
● Dato che in genere i(t) è piccola rispetto alle altre correnti, in prima
approssimazione è possibile trattarla come sinusoidale, attribuendole
un valore efficace pari a quello della corrente distorta
34
Distorsione della corrente magnetizzante (2)
t
i
i
t
35
Distorsione della corrente magnetizzante (3)
i
it
fondamentale
3a armonica
5a armonica
t
36
Distorsione della corrente magnetizzante (4)
● In presenza di isteresi, alla corrente i(t) si aggiunge una componente
ih(t) di pulsazione , sfasata in quadratura in anticipo rispetto a i(t)
● La corrente ih(t) risulta in quadratura in anticipo rispetto al flusso e
quindi è in fase con la tensione e1(t)
Si ha un assorbimento di potenza attiva, che corrisponde alle perdite
nel ferro per isteresi
Il contributo di ih(t) può essere incluso in ia(t) dimensionando
opportunamente R0
37
Distorsione della corrente magnetizzante (5)
t
i
i
t
38
Distorsione della corrente magnetizzante (6)
i
i t
it
iht
t
39
Distorsione del flusso (1)
● Se il trasformatore è fatto funzionare in modo da imporre un andamento
sinusoidale alla corrente magnetizzante, per effetto della non linearità
del nucleo risulta distorto il flusso
● In queste condizioni anche le tensioni sono distorte
● Come si vedrà in seguito, questa situazione si può verificare, ad
esempio, nei sistemi trifase
● Si può dimostrare che, in questo caso, il flusso contiene armoniche
dispari e che il contributo dominante è dovuto alla terza armonica, che
risulta in fase con il flusso stesso
40
Distorsione del flusso (2)
i
i
t
t
41
Distorsione del flusso (3)
fondamentale
t
3a armonica
5a armonica
t
42
Dati di targa
● Un trasformatore è caratterizzato da un insieme di valori nominali che
ne definiscono le prestazioni ai fini delle garanzie e del collaudo
● Questi valori, assieme ad altre informazioni, sono riportati su una targa
apposta sul trasformatore (dati di targa)
● Alcuni dei principali dati di targa sono:
Frequenza nominale: fn [Hz]
Tensione nominale primaria (valore efficace): V1n [V]
Tensione nominale secondaria a vuoto (valore efficace): V20 [V]
Rapporto nominale di trasformazione: K0 V1n / V20
Potenza nominale (apparente): Sn V1n · I1n V20·I2n [VA]
Corrente nominale primaria (valore efficace): I1n [A]
Corrente nominale secondaria (valore efficace): I2n [A]
43
Prova a vuoto (1)
● Al primario viene applicata una tensione di valore nominale
● Il secondario viene lasciato aperto I2 0
● Corrente del primario
I1 I I a I 0
il valore è molto inferiore al valore nominale
le perdite nel rame sono trascurabili
● La caduta di tensione su R2 e Ld2 è nulla
● La caduta di tensione su R1 e Ld1 e molto piccola rispetto al valore in
condizioni nominali
il rapporto V1/V2 si identifica con quello di un trasformatore ideale
V1 N1
K 0 (rapporto di trasformazione nominale)
V2 N 2
● E1 e quindi Ia hanno praticamente i valori nominali
le perdite nel ferro coincidono con quelle relative al funzionamento
nominale
44
Prova a vuoto (2)
● Il comportamento a vuoto del trasformatore può essere descritto
mediante i parametri:
Corrente a vuoto percentuale
I
i0 % 10 100
I10 = corrente a vuoto del primario
I1 n
Potenza a vuoto percentuale
P
P0 % 0 100
P0 = potenza attiva assorbita a vuoto
Sn
Fattore di potenza a vuoto
P
cos 0 0
V1n I10
● I tre parametri non sono indipendenti tra loro dato che risulta
V I cos 0
P0 % 1 n 10
100 i0 % cos 0
V1 n I1n
45
Prova a vuoto (3)
● Noti i parametri Sn, V1n, i0% e cos0, facendo riferimento al circuiti
equivalenti semplificati, è possibile calcolare i valori di R0 e X0
P0
i0 % cos 0
Sn
100
Q0 P0 tan(arccos 0 )
V12n
R0
P0
V12n
X0
Q0
46
Prova in cortocircuito (1)
● Se il secondario è chiuso in cortocircuito V2 = 0 V12 = 0
● L’impedenza R0 X0 è in parallelo con l’impedenza R12 Ld12
R0 e X0 possono essere trascurate perché normalmente R12 e Ld12
sono molto piccole
Corrente del primario
I1
V1
V1
R1 jLd 1 R12 jLd 12 R1cc jL1cc
47
Prova in cortocircuito (2)
● Le impedenze dovute alle resistenze di degli avvolgimenti e alle
induttanze di dispersione sono molto piccole
● Se la tensione a primario ha valore nominale le correnti possono
risultare molto grandi rispetto ai valori nominali
eccessivo surriscaldamento dovuto all’effetto Joule
possibili danni dovuti alle forze tra gli avvolgimenti prodotte
dalle correnti
● Nella prova in cortocircuito il trasformatore viene alimentato con
una tensione V1cc , di valore efficace inferiore a V1, tale da fare
circolare nel secondario una corrente di valore nominale
48
Prova in cortocircuito (3)
● Le correnti I1 e I2 hanno valore nominale (a rigore questo vale
solo per il I2, ma con ottima approssimazione si può ritenere
verificato anche per I1)
le perdite nel rame sono praticamente coincidenti con quelle
relative al funzionamento nominale
● V1 ha un valore molto inferiori a quello nominale
la corrente Ia e I hanno valori molto piccoli rispetto ai valori
in condizioni nominali
le perdite nel ferro sono trascurabili
il rapporto I1/I2 si identifica con quello di un trasformatore
ideale
I1 N 2
I 2 N1
49
Prova in cortocircuito (4)
● Il comportamento del trasformatore in cortocircuito può essere
descritto mediante i parametri:
Tensione di cortocircuito percentuale
V
vcc % 1cc 100
(V1cc = Tensione di cortocircuito del primario)
V1 n
Potenza di cortocircuito percentuale
P
Pcc % cc 100
(Pcc = potenza attiva assorbita in cortocircuito)
Sn
Fattore di potenza in cortocircuito
P
cos cc cc
V1cc I1 n
● I tre parametri non sono indipendenti tra loro dato che risulta
V I cos cc
100 vcc % cos cc
Pcc % 1cc 1n
V1n I1n
50
Prova in cortocircuito (5)
● Noti i parametri Sn, V1n, V20, vcc% e coscc, facendo riferimento ai circuiti
equivalenti semplificati, è possibile calcolare i valori di R1cc e X1cc o di
R2cc e X2cc
Pcc
vcc % cos cc
Sn
100
Qcc Pcc tan(arccos cc )
Sn
V1n
P
R1cc cc2
I1 n
Q
X 1cc 2cc
I1 n
I1 n
Sn
V20
P
R2 cc 2cc
I 2n
Q
X 2 cc 2cc
I2n
I2n
51
Triangolo di cortocircuito
● Il funzionamento dei due circuiti equivalenti può essere rappresentato
mediante i seguenti diagrammi fasoriali
● Il triangolo formato da V2CC e dalle sue componenti resistiva e reattiva è
detto triangolo di cortocircuito del trasformatore
● Il triangolo di cortocircuito è definito dai valori di vcc% e coscc (di regola
riportati sulla targa del trasformatore)
vcc %
V1cc
V
100 2 cc 100
V1n
V20
52
Caduta di tensione (1)
● La caduta di tensione è definita come differenza tra i valori efficaci
della tensione del secondario a vuoto e a carico
V V20 V2
● La caduta di tensione percentuale è definita dalla relazione
V %
V20 V2
100
V20
● Per ottenere una valutazione approssimata della caduta di tensione si
può fare uso alla rete equivalente di Kapp riferita a secondario
53
Caduta di tensione (2)
● Il funzionamento può essere rappresentato mediante il seguente
diagramma fasoriale
● Dato che le cadute di tensione su R2cc e X2cc di solito sono piccole, si
può confondere la differenza tra i moduli di V20 e V2 con la lunghezza
del segmento AE
AE AC cos(cc ) AB cos BC sen
V Z 2 cc I 2 cos(cc ) R2 cc I 2 cos X 2 cc I 2 sen
54
Caduta di tensione (3)
● La caduta di tensione si annulla se l’angolo j di sfasamento tra la
tensione la corrente del carico vale
R
V 0 R2 cc cos X 2 cc sen 0 arctg 2 cc
X 2 cc
● La caduta di tensione è positiva con carichi ohmico-induttivi o con
carichi ohmico-capacitivi che introducono sfasamenti non troppo elevati
R
arctg 2 cc
V 0
2
X 2 cc
caduta di tensione
● La caduta di tensione è negativa (e quindi la tensione a carico ha valore
efficace maggiore di quello a vuoto) se vale la condizione
R
arctg 2 cc V 0
2
X 2 cc
aumento di tensione
55
Rendimento
● Trasformatore alimentato a primario da una tensione sinusoidale
con il secondario collegato ad un impedenza di carico
● Rendimento
P2
P1
P1 potenza attiva assorbita dal primario
P2 potenza attiva ceduta al carico
● I trasformatori, essendo macchine statiche, hanno rendimenti
molto elevati (oltre il 99.5% per i trasformatori di grande potenza)
La definizione non è adatta per la misura del rendimento
P1 e P2 sono poco diverse tra loro la valutazione del
rapporto è molto sensibile agli errori di misura
Le potenze in gioco possono essere molto elevate
56
Rendimento convenzionale
● Il rendimento convenzionale è definito dalla relazione
C
Sn
S n PCu PFe
Sn potenza nominale del trasformatore
PCu potenza dissipata a causa delle perdite nel rame
PFe potenza dissipata a causa delle perdite nel ferro
● La misura del rendimento convenzionale del trasformatore
richiede la valutazione delle perdite nel rame e nel ferro
può essere effettuata mediante una prova in cortocircuito e una
prova a vuoto
57
Parallelo di trasformatori (1)
● Spesso per trasferire energia tra due linee si utilizzano due o più
trasformatori collegati in parallelo
Se il carico è variabile, utilizzando un solo trasformatore dimensionato in funzione della potenza massima, si potrebbero avere periodi
in cui la potenza è molto inferiore alla potenza nominale ( basso
rendimento)
In questo caso conviene utilizzare più trasformatori che possano
essere inseriti progressivamente in parallelo tra loro all’aumentare
della potenza richiesta
In questo modo i trasformatori lavorano in condizioni più vicine a
quelle nominali ( migliore rendimento)
Inoltre la presenza di più trasformatori in parallelo consente di
garantire la continuità del servizio se è necessario scollegare uno
dei trasformatori per guasto o per manutenzione
58
Parallelo di trasformatori (2)
59
Parallelo di trasformatori (3)
● Condizioni di funzionamento ottimali
Il rendimento è il massimo consentito dai due trasformatori
questo in particolare richiede che, in assenza del carico,
le correnti I2a e I2b siano uguali a zero
(altrimenti si avrebbe una corrente nella maglia formata
dai due secondari che darebbe luogo a dissipazioni)
Il carico si ripartisce in quote proporzionali alle potenze
nominali del trasformatori
questo in particolare richiede il parallelo si comporti come
un trasformatore con potenza nominale pari alla somma
delle potenze nominali dei due trasformatori
60
Parallelo di trasformatori (4)
● Affinché sia verificata la prima condizione, occorre che la f.e.m. totale
agente nella maglia formata dai secondari dei trasformatori sia nulla
V20 a V20 b 0
● Dato che le tensioni al primario
sono uguali si ha
V20 a K a V1
V20 b K b V1
Quindi occorre che
I rapporti di trasformazione
siano uguali
Ka Kb
I terminali dei secondari siano
collegati in modo che le f.e.m.
risultino in fase tra loro
61
Parallelo di trasformatori (5)
● Per quanto riguarda il secondo punto, in condizioni nominali si deve
avere
S n V2 n I 2 n S na S nb V2 n I 2 na V2 n I 2 nb
● Quindi le correnti dei secondari devono poter assumere entrambe valori
nominali ed essere in fase tra loro, in modo che risulti
I 2 n I 2 na I 2 nb
● Se le f.e.m. sono uguali, in ogni condizione di funzionamento risulta
Z 2 cca I 2 a R2 cca jX 1cca I 2 a Z 2 ccb I 2 b R2 ccb jX 1ccb I 2 b
● Se si impone che entrambe le correnti assumano i valori nominali
e che siano in fase tra loro, dalla relazione precedente si ricava
R2 cca I 2na R2 ccb I 2 nb
X 1cca I 2na X 1ccb I 2 nb
62
Parallelo di trasformatori (6)
● Le ultime condizioni corrispondono al fatto che i due trasformatori
devono avere triangoli di cortocircuito uguali
● Di conseguenza i trasformatori devono avere gli stessi valori
della tensione di cortocircuito
del fattore di potenza in cortocircuito
63
Parallelo di trasformatori (7)
● Se le condizioni precedenti sono soddisfatte, in ogni condizione
di funzionamento si ha
I 2 a Z 2 ccb I 2 na
I 2 b Z 2 cca I 2 nb
● Quindi il rapporto tra le potenze apparenti coincide sempre con il
rapporto tra le potenze nominali
● Il fatto che le correnti siano sempre in fase tra loro comporta che,
per ogni valore di corrente richiesto dal carico, i loro valori efficaci
assumano il valore più piccolo possibile e quindi che la potenza
dissipata sia minima
64